Положим модель сигнала x(t) (рис.2.8а), заданная на бесконечном интервале tÎ(-¥,¥), имеет спектр gx(f), отличный от нуля только на конечном интервале: gx(f)=0 при |f|³F, F<¥ (рис.2.8б), где F - верхняя частота спектра. Такие сигналы называются сигналами (функциями, процессами) с ограниченным или с финитным спектром.

При временной дискретизации сигналов с ограниченным спектром руководствуются теоремой Котельникова, называемой также теоремой отсчетов.
2. 6. 1. Теорема Котельникова. Процесс x (t) с ограниченным спектром полностью определяется последовательностью своих отсчетов (мгновенных значений) {x(kT0), k=0, ±1, ±2,...}, отстоящих друг от друга на интервал T0£ 1/2F. Значение процесса x(t) в произвольный момент времени tÎ(-¥,¥) выражается формулой
 (2.6.1)
(2.6.1)
где {g k (t)=g 0 (t-kT0), k=0, ±1, ±2,...} - семейство так называемых функций отсчетов 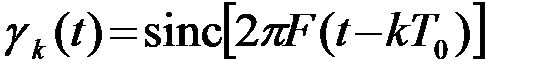 , а g0(t) - нулевая функция отсчетов (2.2.20).
, а g0(t) - нулевая функция отсчетов (2.2.20).
Иначе говоря, теорема утверждает, что процесс x(t), имеющий ограниченный спектр с верхней частотой F может быть разложен в ряд в базисе функций отсчетов {g k (t), k=0, ±1, ±2,...}; при этом коэффициентами ряда будут мгновенные значения процесса xk=x(kT0), взятые с интервалом T0 £ 1/2F.
Для доказательства теоремы введем в рассмотрение функцию
 , (2.6.2
, (2.6.2
представляющую собой периодическую дискретизацию процесса x(t). Спектр произведения функций равен свертке соответствующих спектров. Поэтому спектр  процесса
процесса 
 (2.6.3)
(2.6.3)
и при T<1/2F имеет вид, представленный на рис.2.9а.
Полученная формула (3) выражает закономерность: периодическая дискретизация процесса x(t) с периодом T0 приводит в спектральной области к периодическому повторению спектра gx(f) с периодом 1/T0 (с точностью до коэффициента 1/T0).
Если 1/T0 ³ 2F (T0 £ 1/2F), то соседние полосы спектра  (рис.2.9а) не перекрываются и исходный процесс x(t) может быть выделен из дискретизированного
(рис.2.9а) не перекрываются и исходный процесс x(t) может быть выделен из дискретизированного 
 посредством пропускания последнего через фильтр с коеффициентом передачи (рис.2.9б)
посредством пропускания последнего через фильтр с коеффициентом передачи (рис.2.9б)
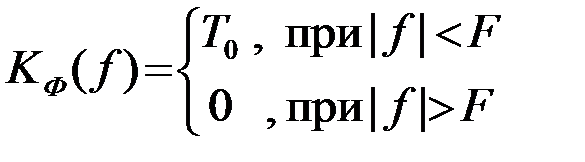 (2.6.4)
(2.6.4)
и соответствующей импульсной характеристикой
 .(2.6.5)
.(2.6.5)
Интервал дискретности желательно иметь побольше. Поэтому в дальнейшем везде принимается
 . (2.6.6)
. (2.6.6)
Импульсная характеристика h Ф (t) при этом совпадает с нулевой функцией отсчетов
 . (2.6.7)
. (2.6.7)
Спектр на выходе фильтра  равен спектру исходного процесса x(t). Следовательно
равен спектру исходного процесса x(t). Следовательно
 .(2.6.8)
.(2.6.8)
После подстановки (2) и (7) в (8) получаем утверждение теоремы (1).

Рис. 2.9
Приведем два обобщения теоремы отсчетов.
Если дискретизирующую функцию сдвинуть во времени на t0, то дискретизированный процесс 

после пропускания через фильтр с характеристикой (7) опять преобразуется в исходный процесс
 (2.6.9)
(2.6.9)
Таким образом, начало t0 отсчетных моментов t0+kT0 при дискретизации можно выбирать произвольно, соответственно сдвигая на t0 в основной формуле (1) функции отсчетов g k.
Теорема отсчетов, приведенная для функции времени x(t) может быть обобщена на функции произвольного аргумента, если прямое  или обратное
или обратное 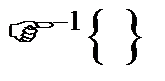 преобразование этих функций отлично от нуля на конечном интервале. Например, если x(t)=0 при |t|> T /2, то спектр gx(f)=F{x(t)} определяется последовательностью своих отсчетов {gx(k/T), k=0,±1,..}, взятых с интервалом дискретности 1/T (заменяется t на f, 2F на T)
преобразование этих функций отлично от нуля на конечном интервале. Например, если x(t)=0 при |t|> T /2, то спектр gx(f)=F{x(t)} определяется последовательностью своих отсчетов {gx(k/T), k=0,±1,..}, взятых с интервалом дискретности 1/T (заменяется t на f, 2F на T)
 .(2.6.10)
.(2.6.10)
Свойства функций отсчета.
- Функции отсчета отличаются друг от друга только временным сдвигом
 .(2.6.11)
.(2.6.11)
- В моменты времени t=kT0 gk(kT0)=1, t=ℓT0 gk(ℓT0)=0 при ℓ¹k, т.е.
 .(2.6.12)
.(2.6.12)
- Спектр функции отсчета gk(t) согласно (2.2.20) равен
 .(2.6.13)
.(2.6.13)
- Если интервал дискретности T0=1/2F, то функции отсчета представляют собой семейство взаимно-ортогональных функций с квадратом нормы (энергией) равным 1/2F

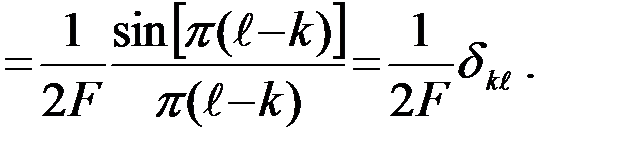 (2.6.14 )
(2.6.14 )
- По отношению к функциям x(t) со спектром, ограниченным частотой  , функции отсчета обладают фильтрующим свойством
, функции отсчета обладают фильтрующим свойством
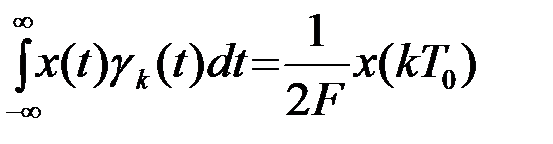 , (2.6.15)
, (2.6.15)
что непосредственно следует, если в (15) подставить (1) и воспользоваться ортогональностью функций отсчета.
- Энергия Э x процесса x(t) вследствие взаимной ортогональности функций отсчета равна
 (2.6.16)
(2.6.16)
Аналогично выражается взаимная энергия двух процессов x(t) и y(t) с ограниченным спектром
 .(2.6.17)
.(2.6.17)
- Иногда интервал дискретности выбирают с запасом T0<1/2F. При этом можно сохранить взаимную ортоганальность функций отсчета, если верхнюю частоту идеального выделяющего фильтра (4) несколько увеличить, приняв  . Соответствующая импульсная характеристика h Ф (t) фильтра, равная нулевой функции отсчета, будет
. Соответствующая импульсная характеристика h Ф (t) фильтра, равная нулевой функции отсчета, будет
 и
и 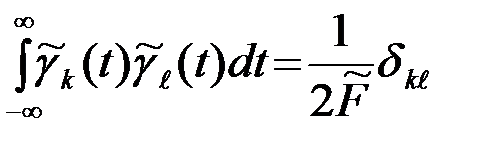 .
.

Рис. 2.10
2.6.3. Следствие теоремы Котельникова. На основании изложенного механизм передачи непрерывных функций x(t) с финитным спектром по каналам связи можно свеcти к следующим операциям (рис.2.10).
- Функция x(t) подвергается дискретизации по времени, т.е. заменяется последовательностью отсчетов {x(kT0)=xk}.
- Полученные числа xk, являющиеся элементарными сообщениями, любым способом передаются по каналу связи с интервалом дискретности T0=1/2F, где F - верхняя частота спектра сообщения x(t).
- На приемной стороне формируются короткие импульсы, площадь(или амплитуда при постоянной длительности) которых пропорциональна отсчетам - элементарным сообщениям. Приближенно формируется последовательность
 .(2.6.18)
.(2.6.18)
- Эта последовательность подается на фильтр нижних частот с частотой среза F. В результате каждый импульс, как показано на рис.2.10, преобразуется в колебание xkgk(t), а последовательность (18) - в сумму åxkgk(t), совпадающую с исходным процессом x(t).
2.6.4. Практические вопросы временной дискретизации. Сообщения, передаваемые по каналам связи (телеметрическая информация, речь, музыка, изображения и т.д.), практически действительно являются функциями с финитным спектром. Например, верхняя частота спектра F примерно равна: для речи 3.5 кГц, для музыки 8 кГц (удовлетворительное воспроизведение), для телевизионных изображений – 6мГц. Некоторая трудность состоит в том, что теорема отсчетов доказана для функций x(t), заданных на неограниченном интервале tÎ(-¥, ¥). Соответственно отсчеты {xk, k=0, ±1, ±2,..} представляют собой бесконечную последовательность. Однако в реальных условиях сообщения x(t)имеют начало и конец, а, следовательно, конечную длительность T<¥. Условия финитности спектра и конечной длительности сообщения, строго говоря, несовместимы. Спектр функции с конечной длительностью теоретически имеет значения, отличные от нуля, при tÎ(-¥, ¥). При любом выборе периода дискретизации T0 сообщения x(t) соседние боковые полосы спектра перекрываются (рис.2.11).

Рис 2.11
При этом выход фильтра с частотой среза F = 1/2T0 не точно воспроизводит исходный процесс x(t). Во-первых, отсекаются частотные составляющие спектра с |f|>F. Во-вторых, в полосу пропускания фильтра попадают "хвосты" соседних боковых полос. Вместе с тем всегда можно определить период дискретизацииT0(или верхнюю частоту спектра F=1/2T0) так, чтобы энергия dЭ x, сосредоточенная в отсекаемых "хвостах" спектра (на частотах f >1/2T0), была пренебрежимо мала по сравнению с энергией всего процесса Эx. Ошибка воспроизведения процесса x(t) на выходе фильтра зависит от отношения dЭ x / Эx и может быть выбором T0 (или F=1/2T0) сделана меньше любой заданной величины. Очевидно, если искажения сообщений, обусловленные временной дискретизацией, будут значительно меньше искажений, обусловленных помехами и допустимых техническими условиями (ТУ) для данной РТС, то такие искажения существенного значения не имеют и могут не учитываться.
Таким образом, приближенно можно принять, что реальные сообщения имеют конечную длительность T и одновременно ограничены по частоте величиной F. При этом бесконечный ряд Котельникова (1) преобразуется в конечный. Число ненулевых отсчетов n примерно равно отношению длительности сообщения к интервалу дискретности:
 .(2.6.19)
.(2.6.19)
Основные формулы теоремы Котельникова для процессов, отличных от нуля на конечном интервале tÎ(0, T), принимают вид:
 (2.6.20)
(2.6.20)
 , (2.6.21)
, (2.6.21)
 .(2.6.22)
.(2.6.22)
Когда процесс {x(t), tÎ(0,T)}определяется конечным числом отсчетов x(0), x(T0),.., x(nT0), в формулах (20)-(22) в отличие от соответствующих точных формул следовало бы писать знак приближенного равенства (@). Однако обычно это не делают. Практически сколько-нибудь заметные искажения появляются только на концах интервала tÎ(0,T).
2.6.5. Временная дискретизация узкополосных сигналов. Спектр gx(f) узкополосного сигнала (радиосигнала) состоит из двух боковых полос (рис.2.12 сплошная линия). Положим, что каждая из полос имеет конечную протяженность 2F. Особенность дискретизации таких сигналов состоит в следующем. Если период дискретизации принять T0=1/2F, то периодическое повторение полосы fÎ(-f0-F, -f0 +F) наложится на полосу fÎ(f0-F, f0+F) (рис.2.12 штриховая линия) и наоборот. В результате в области частот |f|Î(f0-F, f0+F), занятой сигналом x(t), спектр дискретизированного сигнала  не совпадет со спектром исходного сигнала x( t). Формальное применение теоремы отсчетов к рассматриваемому случаю дает для периода дискретизации неоправданно малую величину
не совпадет со спектром исходного сигнала x( t). Формальное применение теоремы отсчетов к рассматриваемому случаю дает для периода дискретизации неоправданно малую величину  .
.
Одной из возможностей осуществления дискретизации радиосигнала x(t) является предварительный переход к аналитическому сигналу  с последующим выделением после дискретизации вещественной части
с последующим выделением после дискретизации вещественной части  . Так как спектр аналитического сигнала отличен от нуля только в полосе fÎ(f0-F, f0+F) (рис.2.6), рассуждения и преобразования при выводе формулы дискретизации аналитического сигнала
. Так как спектр аналитического сигнала отличен от нуля только в полосе fÎ(f0-F, f0+F) (рис.2.6), рассуждения и преобразования при выводе формулы дискретизации аналитического сигнала  не отличаются от приведенных в основной теореме. При дискретизации сигнала
не отличаются от приведенных в основной теореме. При дискретизации сигнала  с периодом T0=1/2F периодически повторяющиеся спектральные полосы не перекрываются. Поэтому исходный сигнал
с периодом T0=1/2F периодически повторяющиеся спектральные полосы не перекрываются. Поэтому исходный сигнал  может быть восстановлен из дискретизированного
может быть восстановлен из дискретизированного  пропусканием последнего через фильтр с частотной характеристикой
пропусканием последнего через фильтр с частотной характеристикой
 (2.6.23)
(2.6.23)
и соответствующей импульсной характеристикой
 .(2.6.24)
.(2.6.24)
При этом
 , (2.6.25)
, (2.6.25)
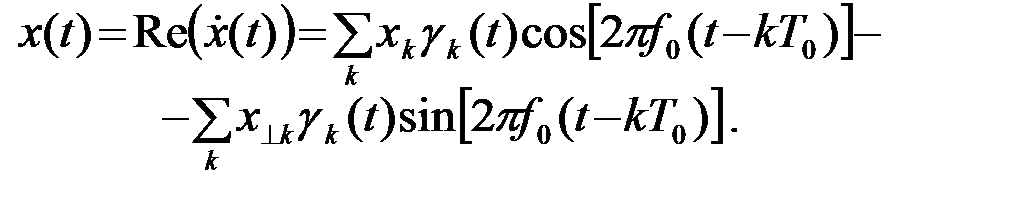 (2.6.26)
(2.6.26)
Особенность состоит в том, что при периодической дискретизации узкополосного сигнала x(t) нужно формировать отсчеты x(kT0) не только исходного процесса x(t), но и отсчеты x^(kT0) сопряженного процесса x^(t). Число отсчетов увеличивается в два раза (n=2×2FT).
В дальнейшем будет показано, что алгоритмы обработки принимаемых сигналов x(t) часто можно свести к обработке их комплексных огибающих  . В этом случае цифровая обработка включает в себя временную дискретизацию комплексной огибающей
. В этом случае цифровая обработка включает в себя временную дискретизацию комплексной огибающей  . Если
. Если  удовлетворяет условиям теоремы отсчетов
удовлетворяет условиям теоремы отсчетов  при | f| > F, то
при | f| > F, то
 .(2.6.27)
.(2.6.27)
Следовательно в этом случае должна быть произведена дискретизация двух квадратурных вещественных составляющих Xc(t) и Xs(t) комплексной огибающей  . Формирование квадратурных составляющих Xc(t) и Xs(t) осуществляется посредством фазового детектирования сигнала x(t) (§8.6).
. Формирование квадратурных составляющих Xc(t) и Xs(t) осуществляется посредством фазового детектирования сигнала x(t) (§8.6).
С теоретической точки зрения обработка с использованием аналитического сигнала  равноценна обработке с использованием комплексной огибающей
равноценна обработке с использованием комплексной огибающей  . С практической точки зрения последняя предпочтительней. Значительно легче точно отсчитать мгновенные значения низкочастотных процессов Xc(t) и Xs(t), чем высокочастотных x(t) и x^(t), так как уменьшается требуемая точность фиксации отсчетных моментов t=kT0.
. С практической точки зрения последняя предпочтительней. Значительно легче точно отсчитать мгновенные значения низкочастотных процессов Xc(t) и Xs(t), чем высокочастотных x(t) и x^(t), так как уменьшается требуемая точность фиксации отсчетных моментов t=kT0.
2.7. Геометрическое представление сигналов (элементы функционального анализа)
В теории РТС в последнее время все шире используются понятия и методы функционального анализа. Основным понятием при этом является множество элементов произвольной природы. Множество, между элементами которого определены некоторые количественные соотношения, называется пространством. Например, пространство, обозначаемое R, является множеством всех действительных чисел xÎ(-¥, ¥). Для дальнейшего наибольший интерес представляет многомерное евклидово пространство R n, имеющее конечное число измерений n. Многомерное пространство с числом измерений n>3 не имеет физического прообраза. Вместе с тем евклидово пространство R n с n>3 является удобной математической абстракцией, обобщающей геометрические закономерности и соотношения, имеющие место в реальном пространстве, на пространство с произвольным конечным числом измерений n.
Евклидово пространство R n представляет собой векторное, метрическое, нормированное пространство. Это значит, что элементами пространства являются n-мерные вектора 
 , где xk, yk Î R, k=1,...,n.
, где xk, yk Î R, k=1,...,n.
Определены операции: сложения векторов
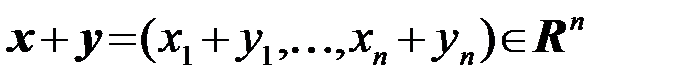 , (2.7.1)
, (2.7.1)
умножение вектора на число a Î R
 , (2.7.2)
, (2.7.2)
скалярного умножения векторов x и y
 .(2.7.3)
.(2.7.3)
В евклидовом пространстве скалярное произведение порождает: метрику пространства r(x,y) - расстояние между элементами пространства (векторами, точками) x и y
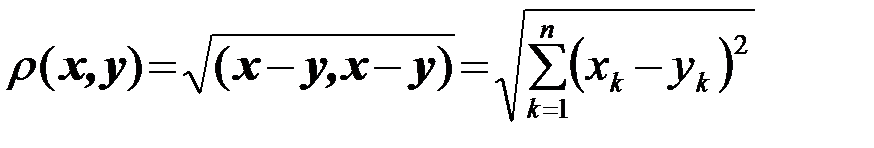 , (2.7.4)
, (2.7.4)
норму || x || - длину вектора x
 (2.7.5)
(2.7.5)
и косинус угла  между векторами x и y
между векторами x и y
 . (2.7.6)
. (2.7.6)
Дальнейшее обобщение - это евклидово пространство с бесконечным, но счетным числом измерений (n=¥), называемое гильбертовым пространством (H). Элементами такого гильбертова пространства являются вектора с бесконечным но счетным числом измерений x =(x1,x2...), y =(y1, y2...) или x =(.., x-2, x-1, x0, x1, x2,..), y=(.., y-2, y-1, y0, y1, y2,..). Все соотношения, приведенные для евклидова пространства, сохраняются для векторного гильбертова пространства при условии, что n=¥, kÎ(1,2...) или kÎ(0, ±1, ±2...).
Другим примером гильбертова пространства является функциональное пространство, элементами которого является множество функций x=x(t), y=y(t) и т.д., интегрируемых в квадрате на интервале T, конечном tÎ(0,T) или бесконечном tÎ(-¥, ¥), также рассматриваемые как вектора или точки пространства. В функциональном гильбертовом пространстве с элементами x=x(t), y=y(t) скалярное произведение выражается формулой
 .(2.7.7)
.(2.7.7)
Соответственно метрика пространства r(x,y) - расстояние между элементами x=x(t) и y=y(t) и норма ||x|| элемента x равны
 , (2.7.8)
, (2.7.8)
 .(2.7.9)
.(2.7.9)
Кроме рассмотренного вещественного пространства используется также комплексное гильбертово пространство, элементами которого являются комплексные функции x=x(t), y=y(t) или комплексные вектора x, y. Особенность состоит в некотором изменении определения скалярного произведения
 .(2.7.10)
.(2.7.10)
Соответственно изменяются выражения для порождаемых скалярным произведением метрики и нормы пространства. Косинус угла для комплексного пространства не определяется.
Наконец, в гильбертовом функциональном пространстве (а также векторном) может быть определено более сложное скалярное произведение - скалярное произведение с весом
 ,
,
где W (t 1, t 2), (W) – симметричная вещественная функция (матрица), например, корреляционная.
Равенство нулю скалярного произведения функций (или векторов) x=x(t) и y=y(t)
 .(2.7.11)
.(2.7.11)
означает их ортогональность.
Совокупность функций (сигналов) называется ортогональной, если две любые функции этой совокупности ортогональны. Если, кроме того, норма каждой функции равна единице, то совокупность называется ортонормированной. Максимальная совокупность взаимноортогональных функций в данном пространстве называется базисом пространства. Базис гильбертова пространства представляет собой бесконечную (но счетную) совокупность ортогональных функций. Как и в реальном пространстве, выбор базиса - системы ортогональных функций (координат), не однозначен.
Если  базис пространства H, то любой элемент x=x(t) пространства H можно представить рядом (вместо k=0, ±1, ±2,... может быть другая бесконечная последовательность, например, k=0, 1, 2,...)
базис пространства H, то любой элемент x=x(t) пространства H можно представить рядом (вместо k=0, ±1, ±2,... может быть другая бесконечная последовательность, например, k=0, 1, 2,...)
 , (2.7.12)
, (2.7.12)
где xk - коэффициенты ряда. Так как
 ,
,
то
 . (2.7.13)
. (2.7.13)
Ряд (12) называют обобщенным рядом Фурье. Он включает в себя традиционный ряд Фурье с базисом экспоненциальных или гармонических функций, а также ряд Котельникова (2.6.1) с базисом функций отсчета {gk(t), k=0, ±1,±2,...}, имеющим норму  . Важно, что представление посредством ряда (12) устанавливает тождественность функции x(t), заданной на конечном или бесконечном интервале T, с дискретной последовательностью - вектором x =(..x-1, x0, x1,..) и, следовательно, возможность замены аналогового сигнала {x(t), tÎT} дискретным x ={xi, i=0, ±1, ±2,..}. Выбор базиса определяется соображениями удобства. Достоинством ряда Котельникова (базиса {gk}) применительно к сигналам с ограниченным спектром является простота определения коэффициентов ряда xk (компонент вектора x), равных мгновенным значениям x(kT0) сигнала x(t).
. Важно, что представление посредством ряда (12) устанавливает тождественность функции x(t), заданной на конечном или бесконечном интервале T, с дискретной последовательностью - вектором x =(..x-1, x0, x1,..) и, следовательно, возможность замены аналогового сигнала {x(t), tÎT} дискретным x ={xi, i=0, ±1, ±2,..}. Выбор базиса определяется соображениями удобства. Достоинством ряда Котельникова (базиса {gk}) применительно к сигналам с ограниченным спектром является простота определения коэффициентов ряда xk (компонент вектора x), равных мгновенным значениям x(kT0) сигнала x(t).
Часто используется приближенное представление элементов (например, сигналов), принадлежащих гильбертову пространству H элементами евклидова пространства R n с той же структурой, т.е. с тем же ортогональным, но конечномерным базисом {yk(t), k=0, 1, 2,..., n}. В терминах обобщенного ряда Фурье бесконечномерный ряд приближается усеченным конечномерным рядом. При этом пространство R n рассматривают как подпространство пространства H. В геометрической интерпретации вектор x =(x1,x2,...)Î H заменяют вектором x =(x1, x2,...,xn)Î R n, который представляет собой проекцию вектора x Î H на подпространство R n.
Евклидово пространство имеет и самостоятельное значение при геометрическом представлении непрерывных функций посредством векторов, так как есть классы сигналов, представимые в конечном ортогональном базисе.
В заключение приводим полученные в §2.6 и широко используемые в дальнейшем приближенные соотношения, выражающие тождественность (взаимно однозначное соответствие) аналоговых сигналов {x(t), tÎ(0, T)} с практически ограниченным спектром и конечномерных векторов x =(x0,..., xn), y =(y0,..., yn).
 (2.7.14)
(2.7.14)
 (2.7.15)
(2.7.15)
шкале уровней.
 .(2.7.16)
.(2.7.16)
Квантование сообщений
В §2.6 было показано, что передачу практически любых сигналов x(t) можно свести к передаче отсчетов - чисел xk=x(kT0), следующих друг за другом с интервалом дискретности T0=1/(2F). Числа эти имеют непрерывную шкалу уровней (значений), т.е. принадлежат континуальному множеству. Дискретизацию сигналов можно продолжить, а именно, подвергнуть отсчеты xk квантованию. Для приближения к реальной ситуации будем полагать, что функция x(t) представляет собой сообщение {l(t), tÎ(0,T)}. Процесс квантования состоит в замене непрерывного множества значений отсчетов lkÎ(lmin, lmax) дискретным множеством {l(1),...,l(m)}. Интервал между соседними уровнями квантования Di=l(i+1)-l(i) называется шагом квантования. Различают равномерное и неравномерное квантование. В большинстве случаев применяется и далее обсуждается равномерное квантование, при котором шаг квантования постоянный Di=D=const. При этом механизм квантования сводится к тому, что вместо данного отсчетного значения lk передается ближайшее значение по разрешенной дискретной Квантование приводит к искажению сообщений. Если квантованное сообщение, полученное в результате квантования отсчета lk=l(kT0), обозначить 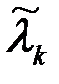 , то
, то

где x k - разность между квантованным сообщением (ближайшим разрешенным уровнем) 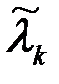 и истинным значением элементарного сообщения lk, называемая шумом квантования.
и истинным значением элементарного сообщения lk, называемая шумом квантования.
На рис.2.13а изображена сетка, определяющая моменты отсчетов и уровни квантования, передаваемое сообщение l(t) (штриховая линия), истинные отсчеты (точки) и квантованные отсчеты (сплошные линии). На рис.2.13б показаны шумы квантования xk. При достаточно большом числе уровней квантования (m³10) шумы xk можно считать взаимно независимыми случайными величинами равномерно распределенными в интервале xkÎ(-D/2, D/2).

Рис. 2.13
Шум квантования оказывает на процесс передачи информации по существу такое же влияние, как и помехи в канале связи. Помехи также как и квантование обуславливают то, что оценки  элементарных сообщений lk, получаемые в РПрУ, отличаются на некоторую величину от истинного значения lk.
элементарных сообщений lk, получаемые в РПрУ, отличаются на некоторую величину от истинного значения lk.
Относительно искажений, обусловленных квантованием, можно высказать те же соображения, которые были приведены в отношении искажений при временной дискретизации. Поскольку на приемной стороне отсчеты воспроизводятся не точно, то не имеет смысла их точно передавать, если это связано с дополнительными затратами. Больше того, абсолютная точность передачи отсчетов, как правило, не требуется. Так, например, при передаче речи и музыки не обнаруживаются искажения, если все отсчеты случайным образом изменить на 1%, при передаче изображений - на 3% и т.д. Можно сказать, что шумы квантования или искажения, обусловленные квантованием, не имеют существенного значения, если эти искажения меньше искажений, обусловленных помехами и допустимых техническими условиями.
С учетом допустимых искажений при высококачественной передаче квантованной речи и музыки используется 128 или 256 уровней квантования, при квантовании движущихся изображений – 32 и т.д.. Заметим, что для передачи речи с удовлетворительной разборчивостью достаточно 32 уровня. Речь сохраняет разборчивость даже при 2-х уровнях квантования: один уровень соответствует положительным значениям отсчетов, другой - отрицательным. Такая "клиппированная речь" даже имеет некоторые преимущества в разборчивости в зашумленных помещениях, например, кабине самолета. Число уровней квантования в телеметрических системах зависит от требуемой точности воспроизведения информации, а также от точности датчиков, осуществляющих сбор этой информации. Причем превышение при квантовании достижимой датчиками или требуемой точности нецелесообразно из-за увеличения энергетических затрат.
В квантованном на m уровней сообщении можно пронумироватьвсе уровни квантования целыми числами (0,1,...m-1) и вместо значения уровня квантования  Î(l(1),...,l(m)) передавать соответствующее целое число NkÎ(0,1,2,...,m-1). Система связи, в которой объектами передачи являются целые числа, называется цифровой системой связи.
Î(l(1),...,l(m)) передавать соответствующее целое число NkÎ(0,1,2,...,m-1). Система связи, в которой объектами передачи являются целые числа, называется цифровой системой связи.
Таким образом, любые сообщения, передаваемые по каналам связи, можно представить в виде последовательности целых чисел N kÎ(0,1,...m-1) или (1,2,...,m), следующих друг за другом с интервалом дискретности T0. При организации связи разработчик системы должен принять решение о целесообразности сохранения непрерывной структуры сообщения, о его частичной (по времени) дискретизации или о полной дискретизации и применении цифровой системы. При цифровой обработке наблюдений аналогичная дискретизация сигналов может производиться на различных этапах обработки.
Радиосигналы связного типа
В настоящем параграфе кратко описаны основные модели радиосигналов связного типа, оптимальный прием которых изучается в последующих главах.
В РПУ в процессе модуляции сообщение накладывается на переносчик информации. В результате формируется радиосигнал. В соответствии с тремя видами сообщений (непрерывные, дискретные, цифровые) различают три вида сигналов.
2.9.1. Непрерывные сигналы. Объектом передачи являются непрерывные собщения l(t), tÎ(0,T), а переносчиком информации гармонические колебания
 .(2.9.1)
.(2.9.1)
В качестве информационного параметра может быть выбран один из трех параметров переносчика: амплитуда, начальная фаза, частота. Соответственно получаются сигналы: 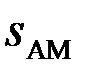 с амплитудной (АМ),
с амплитудной (АМ),  фазовой (ФМ),
фазовой (ФМ),  частотной (ЧМ) модуляцией.
частотной (ЧМ) модуляцией.
 .(2.9.2)
.(2.9.2)
Здесь и далее в моделях непрерывных радиосигналов l(t) - нормированное сообщение  - коэффициент амплитудной модуляции.
- коэффициент амплитудной модуляции.
 ,(2.9.3)
,(2.9.3)
 - индекс ФМ (максимальное отклонение фазы от j0 в процессе ФМ).
- индекс ФМ (максимальное отклонение фазы от j0 в процессе ФМ).
 .(2.9.4)
.(2.9.4)
Закон изменения частоты определяется производной полной фазы колебания y(t)
 ,(2.9.5)
,(2.9.5)
где  - девиация частоты (максимальное отклонение частоты от f0 в процессе ЧМ). Полная фаза y(t) в ЧМ-сигнале (4) равна интегралу функции 2pf(t)
- девиация частоты (максимальное отклонение частоты от f0 в процессе ЧМ). Полная фаза y(t) в ЧМ-сигнале (4) равна интегралу функции 2pf(t)
 .(2.9.6)
.(2.9.6)
Ширина спектра 2Fc радиосигналов определяется формулами (2Fl - ширина спектра сообщения)
 ,(2.9.7)
,(2.9.7)
 ,(2.9.8)
,(2.9.8)
 .(2.9.9)
.(2.9.9)
Обычно последнюю формулу упрощают: если 2Fl>>2  (в 5 и более раз), модуляцию называют узкополосной ЧМ и принимают
(в 5 и более раз), модуляцию называют узкополосной ЧМ и принимают
 .(2.9.10)
.(2.9.10)
Если 2  >>2Fl (в 5 и более раз) модуляцию называют широкополосной ЧМ и принимают
>>2Fl (в 5 и более раз) модуляцию называют широкополосной ЧМ и принимают
 .(2.9.11)
.(2.9.11)
Так, например, в ЧМ радиовещании  =75 кГц. Ширина полосы пропускания РПрУ, равная ширине спектра сигнала, выбирается 150кГц, а РТС ПИ отводится 200 кГц диапазона частот. Фазовая и частотная модуляция имеют много общего и объединяются общим термином угловая модуляция.
=75 кГц. Ширина полосы пропускания РПрУ, равная ширине спектра сигнала, выбирается 150кГц, а РТС ПИ отводится 200 кГц диапазона частот. Фазовая и частотная модуляция имеют много общего и объединяются общим термином угловая модуляция.
2.9.2. Дискретные радиосигналы. (Импульсные аналоговые сигналы). Объектом передачи являются отсчеты сообщения - числа {lk, k=0,1...n}, следующие с интервалом дискретности T0, и принимающие значения из непрерывного интервала lkÎ(lmin, lmax). В процессе формирования радиосигнала используется два переносчика информации: первичный и вторичный. Первичным является периодическая с периодом T0 последовательность видео-импульсов, которым стремятся по возможности придать прямоугольную форму П(t) (рис.2.14а)
 .(2.9.12)
.(2.9.12)
В качестве информационного параметра, изменяющегося пропорционально передаваемому элементарному сообщению lk, можно использовать один из трех параметров видеоимпульса: амплитуду A0, длительность t0, временное положение tk=kT0. Соответственно имеется три вида импульсной модуляции: амплитудно - импульсная модуляция (АИМ), импульсная модуляция по длительности (ДИМ), называемая также широтной (ШИМ), и временная импульсная модуляция (ВИМ), называемая также фазовой (ФИМ). В последнем определении имеется в виду, что изменяется в процессе модуляции фазовое положение импульса на периоде повторения T0. Аналитические выражения для модулированных последовательностей импульсов (видеосигналов) имеют вид
 ,(2.9.13)
,(2.9.13)
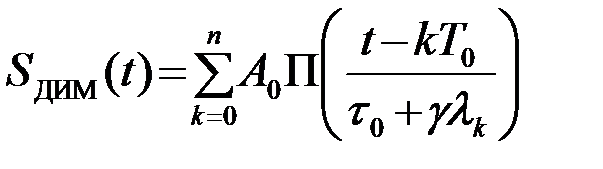 ,(2.9.14)
,(2.9.14)
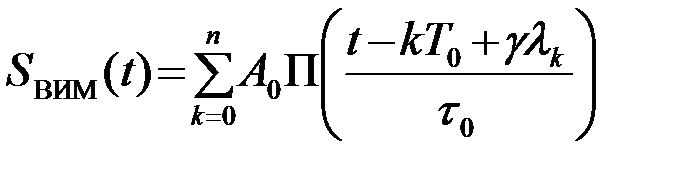 ,(2.9.15)
,(2.9.15)
где g - коэффициент, выбираемый для различных видов модуляции из различных условий. Для сигналов АИМ амплитуда импульсов во всех случаях должна быть положительной A0+glk ³ 0; для сигналов ДИМ длительность импульсов должна быть больше некоторой минимальнойвеличины t0 + glk ³ tmin; для сигналов ВИМ временной сдвиг импульсов не должен превосходить некоторую максимальную величину |glk| £ Dt.
На рис.2.14в,г,д показаны сигналы с первичной импульсной модуляцией: АИМ, ДИМ, ВИМ, соответствующие сообщению, изображаемому на рис.2.14б. Для передачи по радио видеосигнал накладывается на вторичный переносчик информации - высокочастотное гармоническое колебание. Излучаемые радиоимпульсы, соответствующие видео импульсам АИМ, ДИМ, ВИМ (рис.2.14), показаны на рис.2.15.
Скважность импульсных сигналов, равная отношению периода повторения к длительности импульса T0/t0, велика - порядка 103. Поэтому в промежутках между импульсами, отображающими одну программу, например l(t), в РТС можно передавать импульсы, отображающие другие программы m(t), n(t) и т.д. Импульсы различных программ разнесены по времени (не перекрываются) и могут быть разделены на приемной стороне. Эта возможность используется для построения многоканальных телеметрических и связных систем, предназначенных для передачи посредством одной РТС большого числа программ (каналов).

Рис 2.14

Рис 2.15
2.9.3. Цифровые радиосигналы. Объектами передачи являются целые числа {Nk, k=0,1,...,m-1}, следующие друг за другом с интервалом дискретностии T0 и отображающие квантованные отсчеты сообщения. Каждое из этих чисел может принимать одно из m значений NkÎ(0,1,...,m-1). Наибольшее распространение получили цифровые системы передачи информации с кодово-импульсной модуляцией (КИМ), используется также термин "имульсно-кодовая модуляция" - ИКМ, в которых целые числа Nk записываются и передаются в двоичной системе счисления Nk=ak,ℓ ak, ℓ-1...ak,1, где ak,i- двоичные числа i-го разряда при передаче k-го отсчета Nk: ak,iÎ(0,1), ℓ - число двоичных разрядов.
Обычно число возможных значений квантованного элементарного сообщения выбирают целой степенью 2 (25=32, 27=128, 28=256 и т.д.), так что число двоичных разрядов ℓ =log2m. На рис.2.16 показано преобразование цифрового сообщения (ℓ =6, m=64) Nk=44=101100 в видеосигнал КИМ. Интервал длительностью Tc, отводимый для передачи отсчета Nk, разбивается на ℓ подынтервалов длительностью D=Tc/ ℓ. На каждом подынтервале передается двоичное число aÎ(0,1). Единицам соответствует импульс положительной полярности, нулям - отсутствие импульса на подынтервале (рис.2.16а) или импульс отрицательной полярности (рис.2.16б).

Видео-сигнал КИМ накладывается на переносчик информации - высокочастотное гармоническое колебание. В зависимости от того, какой параметр переносчика принят в качестве информационного и изменяется в процессе модуляции, различают три вида радиосигналов КИМ: с амплитудной м




 (2.6.1)
(2.6.1)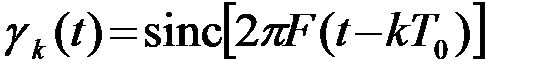 , а g0(t) - нулевая функция отсчетов (2.2.20).
, а g0(t) - нулевая функция отсчетов (2.2.20). , (2.6.2
, (2.6.2 процесса
процесса 
 (2.6.3)
(2.6.3) (рис.2.9а) не перекрываются и исходный процесс x(t) может быть выделен из дискретизированного
(рис.2.9а) не перекрываются и исходный процесс x(t) может быть выделен из дискретизированного 
 посредством пропускания последнего через фильтр с коеффициентом передачи (рис.2.9б)
посредством пропускания последнего через фильтр с коеффициентом передачи (рис.2.9б)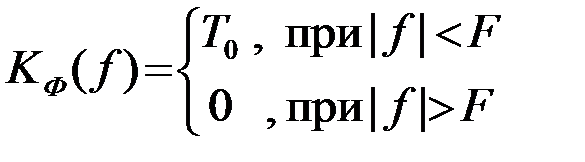 (2.6.4)
(2.6.4) .(2.6.5)
.(2.6.5) . (2.6.6)
. (2.6.6) . (2.6.7)
. (2.6.7) равен спектру исходного процесса x(t). Следовательно
равен спектру исходного процесса x(t). Следовательно .(2.6.8)
.(2.6.8)


 (2.6.9)
(2.6.9) или обратное
или обратное  преобразование этих функций отлично от нуля на конечном интервале. Например, если x(t)=0 при |t|> T /2, то спектр gx(f)=F{x(t)} определяется последовательностью своих отсчетов {gx(k/T), k=0,±1,..}, взятых с интервалом дискретности 1/T (заменяется t на f, 2F на T)
преобразование этих функций отлично от нуля на конечном интервале. Например, если x(t)=0 при |t|> T /2, то спектр gx(f)=F{x(t)} определяется последовательностью своих отсчетов {gx(k/T), k=0,±1,..}, взятых с интервалом дискретности 1/T (заменяется t на f, 2F на T) .(2.6.10)
.(2.6.10) .(2.6.11)
.(2.6.11) .(2.6.12)
.(2.6.12) .(2.6.13)
.(2.6.13)
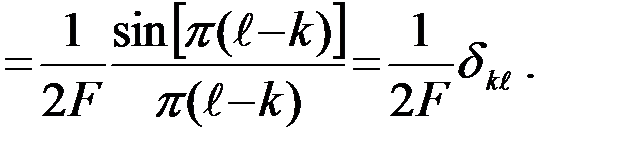 (2.6.14 )
(2.6.14 ) , функции отсчета обладают фильтрующим свойством
, функции отсчета обладают фильтрующим свойством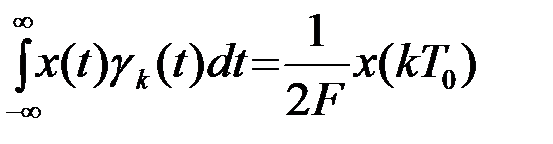 , (2.6.15)
, (2.6.15) (2.6.16)
(2.6.16) .(2.6.17)
.(2.6.17) . Соответствующая импульсная характеристика h Ф (t) фильтра, равная нулевой функции отсчета, будет
. Соответствующая импульсная характеристика h Ф (t) фильтра, равная нулевой функции отсчета, будет и
и 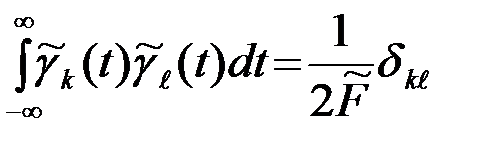 .
.
 .(2.6.18)
.(2.6.18)
 .(2.6.19)
.(2.6.19) (2.6.20)
(2.6.20) , (2.6.21)
, (2.6.21) .(2.6.22)
.(2.6.22) не совпадет со спектром исходного сигнала x( t). Формальное применение теоремы отсчетов к рассматриваемому случаю дает для периода дискретизации неоправданно малую величину
не совпадет со спектром исходного сигнала x( t). Формальное применение теоремы отсчетов к рассматриваемому случаю дает для периода дискретизации неоправданно малую величину  .
. с последующим выделением после дискретизации вещественной части
с последующим выделением после дискретизации вещественной части  . Так как спектр аналитического сигнала отличен от нуля только в полосе fÎ(f0-F, f0+F) (рис.2.6), рассуждения и преобразования при выводе формулы дискретизации аналитического сигнала
. Так как спектр аналитического сигнала отличен от нуля только в полосе fÎ(f0-F, f0+F) (рис.2.6), рассуждения и преобразования при выводе формулы дискретизации аналитического сигнала  не отличаются от приведенных в основной теореме. При дискретизации сигнала
не отличаются от приведенных в основной теореме. При дискретизации сигнала  с периодом T0=1/2F периодически повторяющиеся спектральные полосы не перекрываются. Поэтому исходный сигнал
с периодом T0=1/2F периодически повторяющиеся спектральные полосы не перекрываются. Поэтому исходный сигнал  может быть восстановлен из дискретизированного
может быть восстановлен из дискретизированного  пропусканием последнего через фильтр с частотной характеристикой
пропусканием последнего через фильтр с частотной характеристикой (2.6.23)
(2.6.23) .(2.6.24)
.(2.6.24) , (2.6.25)
, (2.6.25)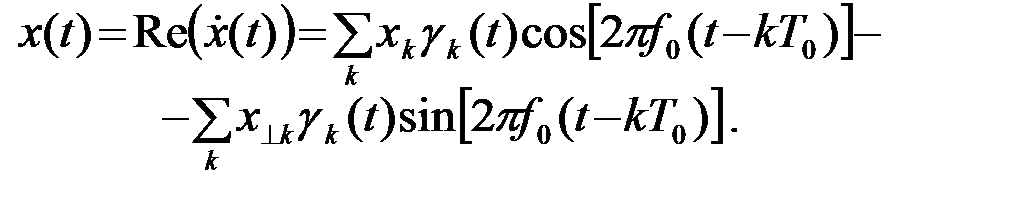 (2.6.26)
(2.6.26) . В этом случае цифровая обработка включает в себя временную дискретизацию комплексной огибающей
. В этом случае цифровая обработка включает в себя временную дискретизацию комплексной огибающей  . Если
. Если  удовлетворяет условиям теоремы отсчетов
удовлетворяет условиям теоремы отсчетов  при | f| > F, то
при | f| > F, то .(2.6.27)
.(2.6.27) равноценна обработке с использованием комплексной огибающей
равноценна обработке с использованием комплексной огибающей  . С практической точки зрения последняя предпочтительней. Значительно легче точно отсчитать мгновенные значения низкочастотных процессов Xc(t) и Xs(t), чем высокочастотных x(t) и x^(t), так как уменьшается требуемая точность фиксации отсчетных моментов t=kT0.
. С практической точки зрения последняя предпочтительней. Значительно легче точно отсчитать мгновенные значения низкочастотных процессов Xc(t) и Xs(t), чем высокочастотных x(t) и x^(t), так как уменьшается требуемая точность фиксации отсчетных моментов t=kT0. , где xk, yk Î R, k=1,...,n.
, где xk, yk Î R, k=1,...,n.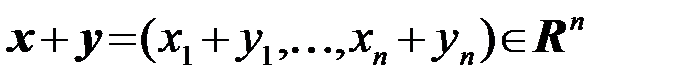 , (2.7.1)
, (2.7.1) , (2.7.2)
, (2.7.2) .(2.7.3)
.(2.7.3)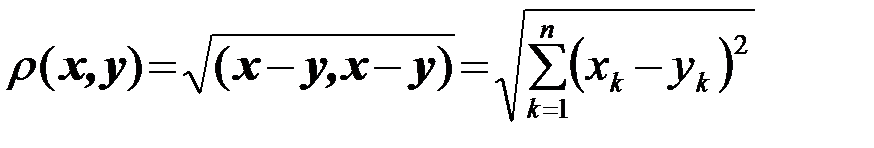 , (2.7.4)
, (2.7.4) (2.7.5)
(2.7.5) между векторами x и y
между векторами x и y . (2.7.6)
. (2.7.6) .(2.7.7)
.(2.7.7) , (2.7.8)
, (2.7.8) .(2.7.9)
.(2.7.9) .(2.7.10)
.(2.7.10) ,
, .(2.7.11)
.(2.7.11) базис пространства H, то любой элемент x=x(t) пространства H можно представить рядом (вместо k=0, ±1, ±2,... может быть другая бесконечная последовательность, например, k=0, 1, 2,...)
базис пространства H, то любой элемент x=x(t) пространства H можно представить рядом (вместо k=0, ±1, ±2,... может быть другая бесконечная последовательность, например, k=0, 1, 2,...) , (2.7.12)
, (2.7.12) ,
, . (2.7.13)
. (2.7.13) . Важно, что представление посредством ряда (12) устанавливает тождественность функции x(t), заданной на конечном или бесконечном интервале T, с дискретной последовательностью - вектором x =(..x-1, x0, x1,..) и, следовательно, возможность замены аналогового сигнала {x(t), tÎT} дискретным x ={xi, i=0, ±1, ±2,..}. Выбор базиса определяется соображениями удобства. Достоинством ряда Котельникова (базиса {gk}) применительно к сигналам с ограниченным спектром является простота определения коэффициентов ряда xk (компонент вектора x), равных мгновенным значениям x(kT0) сигнала x(t).
. Важно, что представление посредством ряда (12) устанавливает тождественность функции x(t), заданной на конечном или бесконечном интервале T, с дискретной последовательностью - вектором x =(..x-1, x0, x1,..) и, следовательно, возможность замены аналогового сигнала {x(t), tÎT} дискретным x ={xi, i=0, ±1, ±2,..}. Выбор базиса определяется соображениями удобства. Достоинством ряда Котельникова (базиса {gk}) применительно к сигналам с ограниченным спектром является простота определения коэффициентов ряда xk (компонент вектора x), равных мгновенным значениям x(kT0) сигнала x(t). (2.7.14)
(2.7.14) (2.7.15)
(2.7.15) .(2.7.16)
.(2.7.16)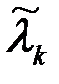 , то
, то

 элементарных сообщений lk, получаемые в РПрУ, отличаются на некоторую величину от истинного значения lk.
элементарных сообщений lk, получаемые в РПрУ, отличаются на некоторую величину от истинного значения lk. .(2.9.1)
.(2.9.1)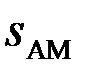 с амплитудной (АМ),
с амплитудной (АМ),  фазовой (ФМ),
фазовой (ФМ),  частотной (ЧМ) модуляцией.
частотной (ЧМ) модуляцией. .(2.9.2)
.(2.9.2) - коэффициент амплитудной модуляции.
- коэффициент амплитудной модуляции. ,(2.9.3)
,(2.9.3) - индекс ФМ (максимальное отклонение фазы от j0 в процессе ФМ).
- индекс ФМ (максимальное отклонение фазы от j0 в процессе ФМ). .(2.9.4)
.(2.9.4) ,(2.9.5)
,(2.9.5) - девиация частоты (максимальное отклонение частоты от f0 в процессе ЧМ). Полная фаза y(t) в ЧМ-сигнале (4) равна интегралу функции 2pf(t)
- девиация частоты (максимальное отклонение частоты от f0 в процессе ЧМ). Полная фаза y(t) в ЧМ-сигнале (4) равна интегралу функции 2pf(t) .(2.9.6)
.(2.9.6) ,(2.9.7)
,(2.9.7) ,(2.9.8)
,(2.9.8) .(2.9.9)
.(2.9.9) .(2.9.10)
.(2.9.10) .(2.9.11)
.(2.9.11) .(2.9.12)
.(2.9.12) ,(2.9.13)
,(2.9.13)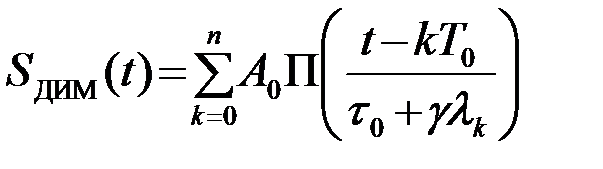 ,(2.9.14)
,(2.9.14)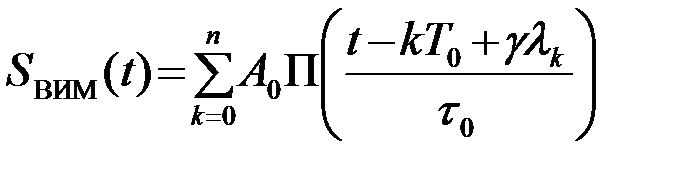 ,(2.9.15)
,(2.9.15)





