BВЕДЕНИЕ
Радиотехнические системы
Радиотехническими системами (РТС) или радиосистемами называются системы, в которых переносчиком или носителем полезной информации являются радиоволны. Различаются несколько типов РТС. Основными являются РТС связного типа (или РТС передачи информации - РТС ПИ) и РТС измерительного типа (или РТС извлечения информации - РТС ИИ), причем РТС ИИ делятся на активные и пассивные.
В РТС связного типа полезная информация, имеющаяся в одном пункте, именуемом передающим, накладывается на радиоволны и передается в другой пункт, именуемый приемным. К РТС связного типа относятся системы радиотелеметрии, радиосвязи и радиовещания, телевидения, радиотелеграфии и др.
Радиотелеметрия - передача по радио результатов измерений параметров различных физических систем. Обычно радиотелеметрия применяется для передачи данных измерений с движущихся или труднодоступных объектов. Например, на летательных аппаратах устанавливаются устройства для контроля режима работы бортовой аппаратуры, для научных исследований окружающего пространства и др. Результаты измерений посредством радио передаются на Землю в пункты, где они регистрируются и обрабатываются.
Радиосвязь и радиовещание - передача по радио речи и музыки.
Телевидение - передача по радио изображений.
Радиотелеграфия - передача по радио буквенных текстов.
В активных РТС измерительного типа полезная информация накладывается на излучаемые РТС радиоволны в процессе их распространения и взаимодействия с окружающей средой и с находящимися в ней объектами. В приемном пункте полезная информация извлекается из радиоволн посредством измерения соответствующих параметров электромагнитного поля. К активным РТС измерительного типа относятся системы: радиолокации, радионавигации, измерения параметров окружающей среды (Земли, ионосферы, тропосферы).
Радиолокация - обнаружение и классификация целей (самолетов, кораблей и т.д.), определение их координат и параметров движения с помощью радиосредств.
Радионавигация - определение местоположения подвижных объектов и обеспечение их движения по заданным траекториям с помощью радиосредств.
Пассивные (неизлучающие) РТС измерительного типа предназначены для измерения параметров собственного излучения окружающей среды. К РТС этого типа относятся системы: радиоастрономии (изучение в научных целях собственного излучения небесных тел), радиоразведки (обнаружение и измерение параметров радиотехнических средств противника), исследования природных ресурсов (посредством изучения собственного излучения Земли). Активные и пассивные РТС, предназначенные для измерения параметров отраженного и собственного излучения Земли и атмосферы, называют РТС дистанционного зондирования.
Несмотря на различие и многообразие перечисленных и не упомянутых РТС, всем им присущи общие закономерности, изучение которых представляет основное содержание учебника. Детальное изучение конкретных РТС, теоретической базой которых является статистическая теория, не входит в нашу задачу. Вместе с тем некоторые сведения о различных типах РТС, необходимые для понимания материала, будут приводиться по мере надобности при изложении.
Для того чтобы охарактеризовать структуру, цели и задачи пособия, а также ввести некоторые исходные определения, рассмотрим в общих чертах структурные схемы основных типов РТС.
Структурные схемы РТС
На рис.1.1 показана структурная схема РТС передачи информации. Она состоит из следующих элементов.
1. Источник сообщений (информации) - устройство, формирующее сообщения: речь, музыку, изображения, телеметрическую информацию (например, закон изменения давления в кабине летательного аппарата) и т.д. Обычно первичные сообщения представляют собой функции времени неэлектрической природы. Для передачи по каналу связи первичные сообщения преобразуются в электрический сигнал, т.е. в колебания электрического тока (или напряжения), изменения которого во времени воспроизводят передаваемое сообщение. Примерами такого преобразования является работа микрофона и телевизионной передающей трубки. В дальнейшем передаваемый электрический сигнал будем называть сообщением и обозначать l(t).
2. Радиопередающее устройство (РПУ) в общем случае выполняет следующие функции. Дискретизация - преобразование непрерывного сообщения - функцииl(t) в дискретную последовательность элементарных сообщений - чисел l. Кодирование элементарных сообщений. При этом сообщениеl преобразуется в комбинацию  сравнительно простых символов
сравнительно простых символов  , обычно двоичных
, обычно двоичных  . Кодирование преследует цель увеличить количество информации, передаваемой в единицу времени и повысить достоверность передачи сообщений. Генерирование высокочастотного колебания - переносчика информации. Модуляция - формирование радиосигнала (высокочастотного сигнала) посредством наложения сообщения l(t) или элементарного сообщения l на переносчик информации. Таким образом, на выходе радиопередатчика формируется радиосигнал, являющийся некоторой функцией s(Ч,Ч) времени tи передаваемого сообщения l(t) или l. При первичном изучении материала будем ориентироваться на передачу элементарных сообщений и соответственно радиосигналовs(t, l), содержащих эти сообщения. В аналоговых РТС дискретизация и кодирование отсутствуют. Функциями РПУ остаются генерирование высокочастотных колебаний и модуляция.
. Кодирование преследует цель увеличить количество информации, передаваемой в единицу времени и повысить достоверность передачи сообщений. Генерирование высокочастотного колебания - переносчика информации. Модуляция - формирование радиосигнала (высокочастотного сигнала) посредством наложения сообщения l(t) или элементарного сообщения l на переносчик информации. Таким образом, на выходе радиопередатчика формируется радиосигнал, являющийся некоторой функцией s(Ч,Ч) времени tи передаваемого сообщения l(t) или l. При первичном изучении материала будем ориентироваться на передачу элементарных сообщений и соответственно радиосигналовs(t, l), содержащих эти сообщения. В аналоговых РТС дискретизация и кодирование отсутствуют. Функциями РПУ остаются генерирование высокочастотных колебаний и модуляция.
3. Линия связи - это физическая среда, в которой распространяется радиосигнал. Колебание на выходе линии связи u(t), которое будем называть принимаемым колебанием или наблюдением, существенно отличается от излученного радиосигнала s(t,l). Во-первых, в процессе распространения радиосигнал ослабляется и приобретает фазовый сдвиг. При этом модель радиосигнала принимает вид es(t,l,j), где e - параметр интенсивности, а j - фазовый сдвиг или начальная фаза. Дополнительные параметры e и j имеют вероятностную природу и могут изменяться во времени - быть функциями e(t) и j(t). Во-вторых, в линии связи к сигналу добавляются помехи различного происхождения: промышленные, атмосферные, космические, от посторонних РТС, внутренние шумы радиоаппаратуры и др. Помехи пересчитываются к выходу линии связи и в дальнейшем обозначаются символом n(t). В результате принимаемое колебание имеет вид:  . Помехи n, суммируемые с сигналом s называют аддитивными в отличие от другого вида помех -мультипликативных, которые возникают в некоторых линиях связи и проявляются в виде произведения помехи, положим e (t), на сигнал: e(t)s(t,l).
. Помехи n, суммируемые с сигналом s называют аддитивными в отличие от другого вида помех -мультипликативных, которые возникают в некоторых линиях связи и проявляются в виде произведения помехи, положим e (t), на сигнал: e(t)s(t,l).
4. Радиоприемное устройство (РПрУ). Назначение РПрУ - с максимально возможной точностью по принятому колебанию u(t) воспроизвести на своем выходе переданное сообщение l или l(t). Принятое (воспроизведенное) сообщение из-за наличия помех в общем случае отличается от посланного. Принятое сообщение будем называть оценкой (имеется в виду оценкой сообщения) и обозначать тем же символом, что и посланное сообщение, но со знаком ^: 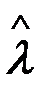 или
или 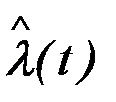 .
.
5. Потребитель - это человек, ЭВМ, какое либо исполнительное или другое устройство, которому предназначены передаваемые сообщения.
Совокупность РПУ, линии связи и РПрУ, ограниченная на рис.1.1 штриховыми линиями, называется каналом связи.
На рис.1.2 изображена структурная схема РТС извлечения информации, имеющая в своем составе излучающую подсистему - РПУ. Особенность ее по сравнению с РТС передачи информации состоит в том, что РПУ излучает в окружающую среду высокочастотные колебания s(t), которые не содержат полезной информации. Информация (сообщение) накладывается на радиоволны в процессе их распространения и взаимодействия с окружающей средой или с подвижными объектами, находящимися в окружающей среде. Так, например, информация о скорости объекта накладывается на переносчик - радиоволны (кодируется) в виде доплеровского сдвига несущей частоты колебаний. Информация о дальности до объекта кодируется в виде временного сдвига (запаздывания) между излученными и принимаемыми колебаниями. Полезную информацию в системах измерительного типа (скорость объектов, их координаты и т.д.) как и ранее обозначим символом l. Как и в РТС передачи информации в линии связи полезный сигнал (излученный сигнал s (t) с наложенной на него информацией – сообщением l) s(t,l) несколько изменяется: ослабляется в e раз и приобретает фазовый сдвиг j. Кроме того к сигналу добавляются упомянутые выше помехи n (t). В результате принимаемое колебание, поступающее на вход РПрУ, опять имеет вид суммы:  . РПрУ формирует
. РПрУ формирует  оценку измеряемого параметра l.
оценку измеряемого параметра l.
Пассивные РТС извлечения информации отличаются от активных (рис.1.2) тем, что они не имеют РПУ. Радиоволны, содержащие полезную информацию l, представляют собственное излучение, сторонних по отношению к РТС объектов. В остальном структурная схема повторяет рис.1.2.
Дельта-функция
Дельта-функцию часто определяют соотношением
 . (2.3.1)
. (2.3.1)
В инженерной практике дельта-функция используется в качестве асимптотической или идеализированной модели короткого импульса dD(t) с единичной площадью. Форма импульса длительности D произвольная. В большинстве случаев
 . (2.3.2)
. (2.3.2)
При этом
 . (2.3.3)
. (2.3.3)
Математически функция определяется своими значениями соответствующими каждому значению аргумента. Ни (1), ни (3) с этим определением не согласуется. Функции (1) и (3) везде равны нулю, кроме одной точки, в которой обращаются в бесконечность - задают величину не имеющую строгого определения. В настоящее время в математике используется широкий класс функций, называемых обобщенными функциями, которые определяются не их значениями, а тем, что они делают при воздействии на обычные функции (или на динамические системы). Функция d(t) является примером обобщенной функции.
Из (1) или (3) следует, что произведение d(t-t0) на произвольную непрерывную в t=t0 функцию j(t) равно:  и представляет собой модель короткого импульса с площадью j(t0). Поэтому
и представляет собой модель короткого импульса с площадью j(t0). Поэтому
 . (2.3.4)
. (2.3.4)
Формула (4) выражает фильтрующее свойство дельта-функции, которое является для нее определяющим. Таким образом, дельта-функция d(t) является обобщенной функцией, свертка которой с произвольной непрерывной функцией j(t) воспроизводит последнюю
 . (2.3.5)
. (2.3.5)
Спектр g(f) функции d(t) согласно (4)
 (2.3.6)
(2.3.6)
имеет постоянное значение, равное 1 при fÎ(-¥,¥).
Обратное преобразование
 .(2.3.7)
.(2.3.7)
Обобщая (7), можно записать
 .(2.3.8)
.(2.3.8)
Последнее выражение используется для определения спектральной плотности гармонических и периодических сигналов (сигналов с неограниченной энергией).
Гармонический сигнал tÎ(-¥,¥)
 . (2.3.9)
. (2.3.9)
Согласно (8)
 . (2.3.10)
. (2.3.10)
Положим, что функция с ограниченной энергией x0(t) равна нулю вне интервала tÎ(-0.5T, 0.5T), т.е. x0(t)=0 при |t|>0.5T. Периодический сигнал с периодом повторения T0 >T
 (2.3.11)
(2.3.11)
может быть представлен рядом Фурье
 .(2.3.12)
.(2.3.12)
Коеффициенты ряда равны
 (2.3.13)
(2.3.13)
где g0(f) - спектр сигнала x0(t): 
Спектральная плотность периодического процесса (12), (13) согласно (8) является дискретной функцией
 .(2.3.14)
.(2.3.14)
Заметим, что функция x0(t) с конечным носителем, т.е. отличная от нуля на конечном интервале |t|£0.5T, также может быть представлена на этом интервале рядом Фурье (12). При этом выражение (12) при подстановке в него (13) может рассматриваться как интегральная сумма, которая при  переходит в преобразование Фурье (2.2.2), а (13) - в (2.2.1).
переходит в преобразование Фурье (2.2.2), а (13) - в (2.2.1).
Пример 2.3.1. В теории сигналов широко используется дискретизирующая (или решетчатая) функция (рис.2.4)
 .(2.3.15)
.(2.3.15)

Определим преобразование Фурье дискретизирующего процесса  . Если принять в (11) x0(t)=d(t) и соответственно
. Если принять в (11) x0(t)=d(t) и соответственно  , то согласно (14)
, то согласно (14)
 (2.3.16)
(2.3.16)
или
 .(2.3.17)
.(2.3.17)
Дискретизирующий процесс во временной области с периодом T0 и дискретизирующий процесс в частотной области с периодом 1/T0 (с точностью до коэффициента 1/T0) являются парой преобразований Фурье. Закономерность (16), (17) можно было получить, представляя рядом Фурье (12) непосредственно дискретизирующую функцию Ш(t, T 0).
Аналитический сигнал
Модель узкополосного радиосигнала (ширина спектра сигнала значительно меньше несущей частоты f0) обычно представляют в виде квазигармонического колебния
 .(2.4.1)
.(2.4.1)
с медленно изменяющимися по сравнению с cos(2pf0t) огибающей A(t) и фазой j(t). Полная фаза колебаний обозначена y (t). Такое определение сигнала x(t) является неоднозначным без дополнительных условий. В (1) можно выбрать различные пары сомножителей A(t) и cos y (t), дающие одно и то же произведение x(t). Разумно потребовать, чтобы модель (1) была такой, при которой огибающая A(t) и сигнал x(t) не пересекались, а точки их касания имели общую касательную. В теоретических и прикладных исследованиях оказалось удобным использовать модель аналитического (комплексного) сигнала  . При этом физический (реальный) сигнал x(t) является вещественной частью аналитического
. При этом физический (реальный) сигнал x(t) является вещественной частью аналитического  . Мнимая часть аналитического сигнала
. Мнимая часть аналитического сигнала  задается преобразованием Гильберта реального сигнала
задается преобразованием Гильберта реального сигнала
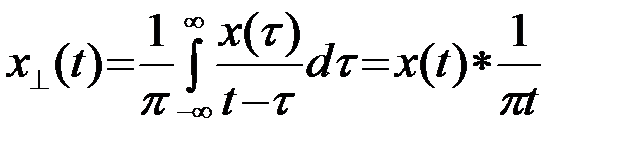 .(2.4.2)
.(2.4.2)
Это обеспечивает однозначное определение огибающей A(t) и полной фазы y(t)=2p¦0t+j(t) сигнала (1), соответствующее физическим представлениям о них
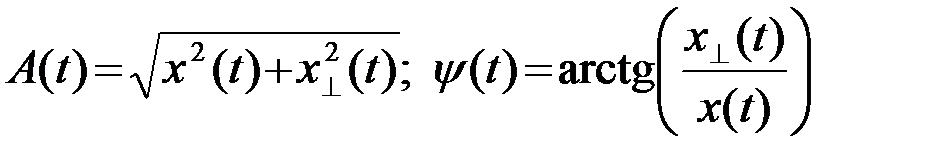 .(2.4.3)
.(2.4.3)
Аналитический сигнал при этом можно записать в показательной форме
 (2.4.4)
(2.4.4)
и представить на комплексной плоскости (рис.2.5) в виде вектора с переменной длиной A(t), вращающегося с переменной угловой скоростью w(t) [рад/с]
 .(2.4.5)
.(2.4.5)
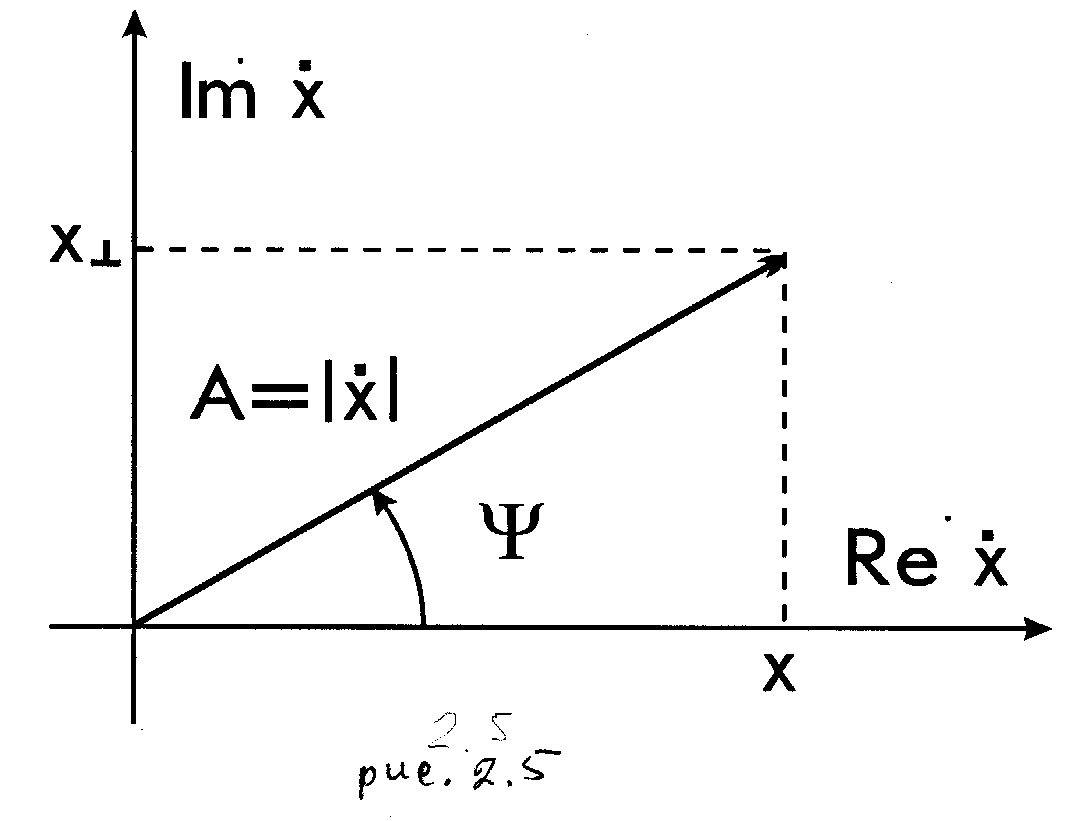
После неоднозначного в общем случае выбора несущей частоты f0 (выбор обсуждается ниже), однозначно определяется закон изменения начальной фазы
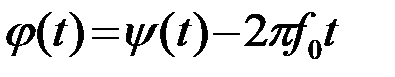 .(2.4.6)
.(2.4.6)
Рассматриваемые сигналы  (рис.2.5) выражаются при этом формулами: (1),
(рис.2.5) выражаются при этом формулами: (1),
 (2.4.7)
(2.4.7)
и
 , (2.4.8)
, (2.4.8)
где 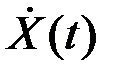 - комплексная огибающая сигнала
- комплексная огибающая сигнала
 .(2.4.9)
.(2.4.9)
Сопряженный (по Гильберту) сигнал x^(t) (7) сдвинут по фазе на p /2 по отношению к реальному сигналу x(t) (1) и называется квадратурным сигналом, а Xc(t) и Xs(t) - вещественная и мнимая составляющие комплексной огибающей  , называемые также квадратурными составляющими комплексной огибающей
, называемые также квадратурными составляющими комплексной огибающей  . Представление радиосигналов на комплексной плоскости (рис.2.5) широко используются при изучении модулированных сигналов (АМ, ФМ, ЧМ).
. Представление радиосигналов на комплексной плоскости (рис.2.5) широко используются при изучении модулированных сигналов (АМ, ФМ, ЧМ).
Рассмотрим еще представление аналитического сигнала  в частотной области. Положим спектр реального сигнала gx(f)=
в частотной области. Положим спектр реального сигнала gx(f)=  {x(t)} (точнее его модуль |gx(f)|) имеет вид, изображенный на рис.2.6а.
{x(t)} (точнее его модуль |gx(f)|) имеет вид, изображенный на рис.2.6а.

В соответствии с общей закономерностью его амплитудный спектр |gx(f)| симметричен относительно оси f=0. Спектр сопряженного x сигнала x^(t), являющегося во временной области сверткой (2), в частотной области будет равен произведению спектров  {x(t)} и (2.2.27)
{x(t)} и (2.2.27)
 .
.
Следовательно
 .(2.4.10)
.(2.4.10)
Амплитудные спектры сопряженных (квадратурных) сигналов x(t) и x^(t) совпадают. Соответственно спектр  совпадает с
совпадает с  , изображенным на рис. 2.6а.
, изображенным на рис. 2.6а.
Свойства функций отсчета.
- Функции отсчета отличаются друг от друга только временным сдвигом
 .(2.6.11)
.(2.6.11)
- В моменты времени t=kT0 gk(kT0)=1, t=ℓT0 gk(ℓT0)=0 при ℓ¹k, т.е.
 .(2.6.12)
.(2.6.12)
- Спектр функции отсчета gk(t) согласно (2.2.20) равен
 .(2.6.13)
.(2.6.13)
- Если интервал дискретности T0=1/2F, то функции отсчета представляют собой семейство взаимно-ортогональных функций с квадратом нормы (энергией) равным 1/2F

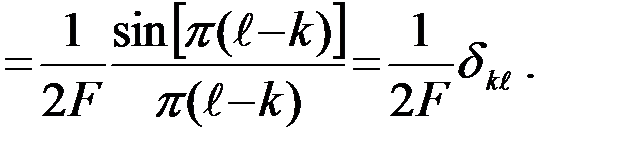 (2.6.14 )
(2.6.14 )
- По отношению к функциям x(t) со спектром, ограниченным частотой  , функции отсчета обладают фильтрующим свойством
, функции отсчета обладают фильтрующим свойством
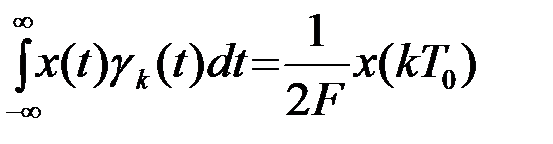 , (2.6.15)
, (2.6.15)
что непосредственно следует, если в (15) подставить (1) и воспользоваться ортогональностью функций отсчета.
- Энергия Э x процесса x(t) вследствие взаимной ортогональности функций отсчета равна
 (2.6.16)
(2.6.16)
Аналогично выражается взаимная энергия двух процессов x(t) и y(t) с ограниченным спектром
 .(2.6.17)
.(2.6.17)
- Иногда интервал дискретности выбирают с запасом T0<1/2F. При этом можно сохранить взаимную ортоганальность функций отсчета, если верхнюю частоту идеального выделяющего фильтра (4) несколько увеличить, приняв  . Соответствующая импульсная характеристика h Ф (t) фильтра, равная нулевой функции отсчета, будет
. Соответствующая импульсная характеристика h Ф (t) фильтра, равная нулевой функции отсчета, будет
 и
и 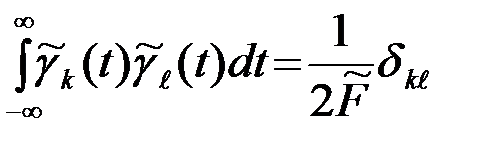 .
.

Рис. 2.10
2.6.3. Следствие теоремы Котельникова. На основании изложенного механизм передачи непрерывных функций x(t) с финитным спектром по каналам связи можно свеcти к следующим операциям (рис.2.10).
- Функция x(t) подвергается дискретизации по времени, т.е. заменяется последовательностью отсчетов {x(kT0)=xk}.
- Полученные числа xk, являющиеся элементарными сообщениями, любым способом передаются по каналу связи с интервалом дискретности T0=1/2F, где F - верхняя частота спектра сообщения x(t).
- На приемной стороне формируются короткие импульсы, площадь(или амплитуда при постоянной длительности) которых пропорциональна отсчетам - элементарным сообщениям. Приближенно формируется последовательность
 .(2.6.18)
.(2.6.18)
- Эта последовательность подается на фильтр нижних частот с частотой среза F. В результате каждый импульс, как показано на рис.2.10, преобразуется в колебание xkgk(t), а последовательность (18) - в сумму åxkgk(t), совпадающую с исходным процессом x(t).
2.6.4. Практические вопросы временной дискретизации. Сообщения, передаваемые по каналам связи (телеметрическая информация, речь, музыка, изображения и т.д.), практически действительно являются функциями с финитным спектром. Например, верхняя частота спектра F примерно равна: для речи 3.5 кГц, для музыки 8 кГц (удовлетворительное воспроизведение), для телевизионных изображений – 6мГц. Некоторая трудность состоит в том, что теорема отсчетов доказана для функций x(t), заданных на неограниченном интервале tÎ(-¥, ¥). Соответственно отсчеты {xk, k=0, ±1, ±2,..} представляют собой бесконечную последовательность. Однако в реальных условиях сообщения x(t)имеют начало и конец, а, следовательно, конечную длительность T<¥. Условия финитности спектра и конечной длительности сообщения, строго говоря, несовместимы. Спектр функции с конечной длительностью теоретически имеет значения, отличные от нуля, при tÎ(-¥, ¥). При любом выборе периода дискретизации T0 сообщения x(t) соседние боковые полосы спектра перекрываются (рис.2.11).

Рис 2.11
При этом выход фильтра с частотой среза F = 1/2T0 не точно воспроизводит исходный процесс x(t). Во-первых, отсекаются частотные составляющие спектра с |f|>F. Во-вторых, в полосу пропускания фильтра попадают "хвосты" соседних боковых полос. Вместе с тем всегда можно определить период дискретизацииT0(или верхнюю частоту спектра F=1/2T0) так, чтобы энергия dЭ x, сосредоточенная в отсекаемых "хвостах" спектра (на частотах f >1/2T0), была пренебрежимо мала по сравнению с энергией всего процесса Эx. Ошибка воспроизведения процесса x(t) на выходе фильтра зависит от отношения dЭ x / Эx и может быть выбором T0 (или F=1/2T0) сделана меньше любой заданной величины. Очевидно, если искажения сообщений, обусловленные временной дискретизацией, будут значительно меньше искажений, обусловленных помехами и допустимых техническими условиями (ТУ) для данной РТС, то такие искажения существенного значения не имеют и могут не учитываться.
Таким образом, приближенно можно принять, что реальные сообщения имеют конечную длительность T и одновременно ограничены по частоте величиной F. При этом бесконечный ряд Котельникова (1) преобразуется в конечный. Число ненулевых отсчетов n примерно равно отношению длительности сообщения к интервалу дискретности:
 .(2.6.19)
.(2.6.19)
Основные формулы теоремы Котельникова для процессов, отличных от нуля на конечном интервале tÎ(0, T), принимают вид:
 (2.6.20)
(2.6.20)
 , (2.6.21)
, (2.6.21)
 .(2.6.22)
.(2.6.22)
Когда процесс {x(t), tÎ(0,T)}определяется конечным числом отсчетов x(0), x(T0),.., x(nT0), в формулах (20)-(22) в отличие от соответствующих точных формул следовало бы писать знак приближенного равенства (@). Однако обычно это не делают. Практически сколько-нибудь заметные искажения появляются только на концах интервала tÎ(0,T).
2.6.5. Временная дискретизация узкополосных сигналов. Спектр gx(f) узкополосного сигнала (радиосигнала) состоит из двух боковых полос (рис.2.12 сплошная линия). Положим, что каждая из полос имеет конечную протяженность 2F. Особенность дискретизации таких сигналов состоит в следующем. Если период дискретизации принять T0=1/2F, то периодическое повторение полосы fÎ(-f0-F, -f0 +F) наложится на полосу fÎ(f0-F, f0+F) (рис.2.12 штриховая линия) и наоборот. В результате в области частот |f|Î(f0-F, f0+F), занятой сигналом x(t), спектр дискретизированного сигнала  не совпадет со спектром исходного сигнала x( t). Формальное применение теоремы отсчетов к рассматриваемому случаю дает для периода дискретизации неоправданно малую величину
не совпадет со спектром исходного сигнала x( t). Формальное применение теоремы отсчетов к рассматриваемому случаю дает для периода дискретизации неоправданно малую величину  .
.
Одной из возможностей осуществления дискретизации радиосигнала x(t) является предварительный переход к аналитическому сигналу  с последующим выделением после дискретизации вещественной части
с последующим выделением после дискретизации вещественной части  . Так как спектр аналитического сигнала отличен от нуля только в полосе fÎ(f0-F, f0+F) (рис.2.6), рассуждения и преобразования при выводе формулы дискретизации аналитического сигнала
. Так как спектр аналитического сигнала отличен от нуля только в полосе fÎ(f0-F, f0+F) (рис.2.6), рассуждения и преобразования при выводе формулы дискретизации аналитического сигнала  не отличаются от приведенных в основной теореме. При дискретизации сигнала
не отличаются от приведенных в основной теореме. При дискретизации сигнала  с периодом T0=1/2F периодически повторяющиеся спектральные полосы не перекрываются. Поэтому исходный сигнал
с периодом T0=1/2F периодически повторяющиеся спектральные полосы не перекрываются. Поэтому исходный сигнал  может быть восстановлен из дискретизированного
может быть восстановлен из дискретизированного  пропусканием последнего через фильтр с частотной характеристикой
пропусканием последнего через фильтр с частотной характеристикой
 (2.6.23)
(2.6.23)
и соответствующей импульсной характеристикой
 .(2.6.24)
.(2.6.24)
При этом
 , (2.6.25)
, (2.6.25)
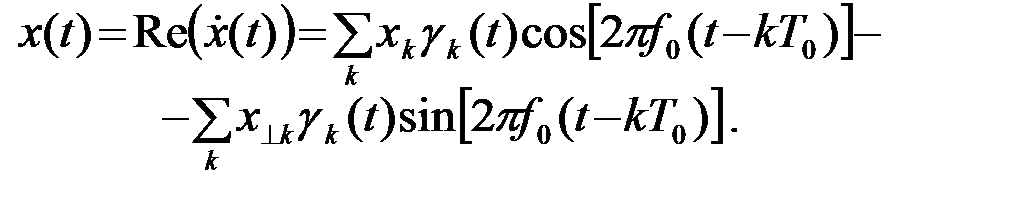 (2.6.26)
(2.6.26)
Особенность состоит в том, что при периодической дискретизации узкополосного сигнала x(t) нужно формировать отсчеты x(kT0) не только исходного процесса x(t), но и отсчеты x^(kT0) сопряженного процесса x^(t). Число отсчетов увеличивается в два раза (n=2×2FT).
В дальнейшем будет показано, что алгоритмы обработки принимаемых сигналов x(t) часто можно свести к обработке их комплексных огибающих  . В этом случае цифровая обработка включает в себя временную дискретизацию комплексной огибающей
. В этом случае цифровая обработка включает в себя временную дискретизацию комплексной огибающей  . Если
. Если  удовлетворяет условиям теоремы отсчетов
удовлетворяет условиям теоремы отсчетов  при | f| > F, то
при | f| > F, то
 .(2.6.27)
.(2.6.27)
Следовательно в этом случае должна быть произведена дискретизация двух квадратурных вещественных составляющих Xc(t) и Xs(t) комплексной огибающей  . Формирование квадратурных составляющих Xc(t) и Xs(t) осуществляется посредством фазового детектирования сигнала x(t) (§8.6).
. Формирование квадратурных составляющих Xc(t) и Xs(t) осуществляется посредством фазового детектирования сигнала x(t) (§8.6).
С теоретической точки зрения обработка с использованием аналитического сигнала  равноценна обработке с использованием комплексной огибающей
равноценна обработке с использованием комплексной огибающей  . С практической точки зрения последняя предпочтительней. Значительно легче точно отсчитать мгновенные значения низкочастотных процессов Xc(t) и Xs(t), чем высокочастотных x(t) и x^(t), так как уменьшается требуемая точность фиксации отсчетных моментов t=kT0.
. С практической точки зрения последняя предпочтительней. Значительно легче точно отсчитать мгновенные значения низкочастотных процессов Xc(t) и Xs(t), чем высокочастотных x(t) и x^(t), так как уменьшается требуемая точность фиксации отсчетных моментов t=kT0.
2.7. Геометрическое представление сигналов (элементы функционального анализа)
В теории РТС в последнее время все шире используются понятия и методы функционального анализа. Основным понятием при этом является множество элементов произвольной природы. Множество, между элементами которого определены некоторые количественные соотношения, называется пространством. Например, пространство, обозначаемое R, является множеством всех действительных чисел xÎ(-¥, ¥). Для дальнейшего наибольший интерес представляет многомерное евклидово пространство R n, имеющее конечное число измерений n. Многомерное пространство с числом измерений n>3 не имеет физического прообраза. Вместе с тем евклидово пространство R n с n>3 является удобной математической абстракцией, обобщающей геометрические закономерности и соотношения, имеющие место в реальном пространстве, на пространство с произвольным конечным числом измерений n.
Евклидово пространство R n представляет собой векторное, метрическое, нормированное пространство. Это значит, что элементами пространства являются n-мерные вектора 
 , где xk, yk Î R, k=1,...,n.
, где xk, yk Î R, k=1,...,n.
Определены операции: сложения векторов
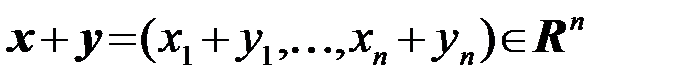 , (2.7.1)
, (2.7.1)
умножение вектора на число a Î R
 , (2.7.2)
, (2.7.2)
скалярного умножения векторов x и y
 .(2.7.3)
.(2.7.3)
В евклидовом пространстве скалярное произведение порождает: метрику пространства r(x,y) - расстояние между элементами пространства (векторами, точками) x и y
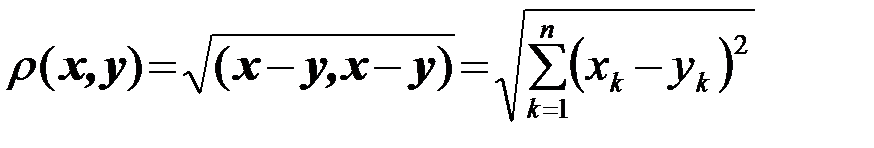 , (2.7.4)
, (2.7.4)
норму || x || - длину вектора x
 (2.7.5)
(2.7.5)
и косинус угла  между векторами x и y
между векторами x и y
 . (2.7.6)
. (2.7.6)
Дальнейшее обобщение - это евклидово пространство с бесконечным, но счетным числом измерений (n=¥), называемое гильбертовым пространством (H). Элементами такого гильбертова пространства являются вектора с бесконечным но счетным числом измерений x =(x1,x2...), y =(y1, y2...) или x =(.., x-2, x-1, x0, x1, x2,..), y=(.., y-2, y-1, y0, y1, y2,..). Все соотношения, приведенные для евклидова пространства, сохраняются для векторного гильбертова пространства при условии, что n=¥, kÎ(1,2...) или kÎ(0, ±1, ±2...).
Другим примером гильбертова пространства является функциональное пространство, элементами которого является множество функций x=x(t), y=y(t) и т.д., интегрируемых в квадрате на интервале T, конечном tÎ(0,T) или бесконечном tÎ(-¥, ¥), также рассматриваемые как вектора или точки пространства. В функциональном гильбертовом пространстве с элементами x=x(t), y=y(t) скалярное произведение выражается формулой
 .(2.7.7)
.(2.7.7)
Соответственно метрика пространства r(x,y) - расстояние между элементами x=x(t) и y=y(t) и норма ||x|| элемента x равны
 , (2.7.8)
, (2.7.8)
 .(2.7.9)
.(2.7.9)
Кроме рассмотренного вещественного пространства используется также комплексное гильбертово пространство, элементами которого являются комплексные функции x=x(t), y=y(t) или комплексные вектора x, y. Особенность состоит в некотором изменении определения скалярного произведения
 .(2.7.10)
.(2.7.10)
Соответственно изменяются выражения для порождаемых скалярным произведением метрики и нормы пространства. Косинус угла для комплексного пространства не определяется.
Наконец, в гильбертовом функциональном пространстве (а также векторном) может быть определено более сложное скалярное произведение - скалярное произведение с весом
 ,
,
где W (t 1, t 2), (W) – симметричная вещественная функция (матрица), например, корреляционная.
Равенство нулю скалярного произведения функций (или векторов) x=x(t) и y=y(t)
 .(2.7.11)
.(2.7.11)
означает их ортогональность.
Совокупность функций (сигналов) называется ортогональной, если две любые функции этой совокупности ортогональны. Если, кроме того, норма каждой функции равна единице, то совокупность называется ортонормированной. Максимальная совокупность взаимноортогональных функций в данном пространстве называется базисом пространства. Базис гильбертова пространства представляет собой бесконечную (но счетную) совокупность ортогональных функций. Как и в реальном пространстве, выбор базиса - системы ортогональных функций (координат), не однозначен.
Если  базис пространства H, то любой элемент x=x(t) пространства H можно представить рядом (вместо k=0, ±1, ±2,... может быть другая бесконечная последовательность, например, k=0, 1, 2,...)
базис пространства H, то любой элемент x=x(t) пространства H можно представить рядом (вместо k=0, ±1, ±2,... может быть другая бесконечная последовательность, например, k=0, 1, 2,...)
 , (2.7.12)
, (2.7.12)
где xk - коэффициенты ряда. Так как
 ,
,
то
 . (2.7.13)
. (2.7.13)
Ряд (12) называют обобщенным рядом Фурье. Он включает в себя традиционный ряд Фурье с базисом экспоненциальных или гармонических функций, а также ряд Котельникова (2.6.1) с базисом функций отсчета {gk(t), k=0, ±1,±2,...}, имеющим норму  . Важно, что представление посредством ряда (12) устанавливает тождественность функции x(t), заданной на конечном или бесконечном интервале T, с дискретной последовательностью - вектором x =(..x-1, x0, x1,..) и, следовательно, возможность замены аналогового сигнала {x(t), tÎT} дискретным x ={xi, i=0, ±1, ±2,..}. Выбор базиса определяется соображениями удобства. Достоинством ряда Котельникова (базиса {gk}) применительно к сигналам с ограниченным спектром является простота определения коэффициентов ряда xk (компонент вектора x), равных мгновенным значениям x(kT0) сигнала x(t).
. Важно, что представление посредством ряда (12) устанавливает тождественность функции x(t), заданной на конечном или бесконечном интервале T, с дискретной последовательностью - вектором x =(..x-1, x0, x1,..) и, следовательно, возможность замены аналогового сигнала {x(t), tÎT} дискретным x ={xi, i=0, ±1, ±2,..}. Выбор базиса определяется соображениями удобства. Достоинством ряда Котельникова (базиса {gk}) применительно к сигналам с ограниченным спектром является простота определения коэффициентов ряда xk (компонент вектора x), равных мгновенным значениям x(kT0) сигнала x(t).
Часто используется приближенное представление элементов (например, сигналов), принадлежащих гильбертову пространству H элементами евклидова пространства R n с той же структурой, т.е. с тем же ортогональным, но конечномерным базисом {yk(t), k=0, 1, 2,..., n}. В терминах обобщенного ряда Фурье бесконечномерный ряд приближается усеченным конечномерным рядом. При этом пространство R n рассматривают как подпространство пространства H. В геометрической интерпретации вектор x =(x1,x2,...)Î H заменяют вектором x =(x1, x2,...,xn)Î R n, который представляет собой проекцию вектора x Î H на подпространство R n.
Евклидово пространство имеет и самостоятельное значение при геометрическом представлении непрерывных функций посредством векторов, так как есть классы сигналов, представимые в конечном ортогональном базисе.
В заключение приводим полученные в §2.6 и широко используемые в дальнейшем приближенные соотношения, выражающие тождественность (взаимно однозначное соответствие) аналоговых сигналов {x(t), tÎ(0, T)} с практически ограниченным спектром и конечномерных векторов x =(x0,..., xn), y =(y0,..., yn).
 (2.7.14)
(2.7.14)
 (2.7.15)
(2.7.15)
шкале уровней.

|
|
|



 сравнительно простых символов
сравнительно простых символов  , обычно двоичных
, обычно двоичных  . Кодирование преследует цель увеличить количество информации, передаваемой в единицу времени и повысить достоверность передачи сообщений. Генерирование высокочастотного колебания - переносчика информации. Модуляция - формирование радиосигнала (высокочастотного сигнала) посредством наложения сообщения l(t) или элементарного сообщения l на переносчик информации. Таким образом, на выходе радиопередатчика формируется радиосигнал, являющийся некоторой функцией s(Ч,Ч) времени tи передаваемого сообщения l(t) или l. При первичном изучении материала будем ориентироваться на передачу элементарных сообщений и соответственно радиосигналовs(t, l), содержащих эти сообщения. В аналоговых РТС дискретизация и кодирование отсутствуют. Функциями РПУ остаются генерирование высокочастотных колебаний и модуляция.
. Кодирование преследует цель увеличить количество информации, передаваемой в единицу времени и повысить достоверность передачи сообщений. Генерирование высокочастотного колебания - переносчика информации. Модуляция - формирование радиосигнала (высокочастотного сигнала) посредством наложения сообщения l(t) или элементарного сообщения l на переносчик информации. Таким образом, на выходе радиопередатчика формируется радиосигнал, являющийся некоторой функцией s(Ч,Ч) времени tи передаваемого сообщения l(t) или l. При первичном изучении материала будем ориентироваться на передачу элементарных сообщений и соответственно радиосигналовs(t, l), содержащих эти сообщения. В аналоговых РТС дискретизация и кодирование отсутствуют. Функциями РПУ остаются генерирование высокочастотных колебаний и модуляция. . Помехи n, суммируемые с сигналом s называют аддитивными в отличие от другого вида помех -мультипликативных, которые возникают в некоторых линиях связи и проявляются в виде произведения помехи, положим e (t), на сигнал: e(t)s(t,l).
. Помехи n, суммируемые с сигналом s называют аддитивными в отличие от другого вида помех -мультипликативных, которые возникают в некоторых линиях связи и проявляются в виде произведения помехи, положим e (t), на сигнал: e(t)s(t,l).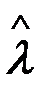 или
или 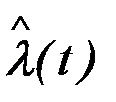 .
. . РПрУ формирует
. РПрУ формирует  оценку измеряемого параметра l.
оценку измеряемого параметра l. . (2.3.1)
. (2.3.1) . (2.3.2)
. (2.3.2) . (2.3.3)
. (2.3.3) и представляет собой модель короткого импульса с площадью j(t0). Поэтому
и представляет собой модель короткого импульса с площадью j(t0). Поэтому . (2.3.4)
. (2.3.4) . (2.3.5)
. (2.3.5) (2.3.6)
(2.3.6) .(2.3.7)
.(2.3.7) .(2.3.8)
.(2.3.8) . (2.3.9)
. (2.3.9) . (2.3.10)
. (2.3.10) (2.3.11)
(2.3.11) .(2.3.12)
.(2.3.12) (2.3.13)
(2.3.13)
 .(2.3.14)
.(2.3.14) переходит в преобразование Фурье (2.2.2), а (13) - в (2.2.1).
переходит в преобразование Фурье (2.2.2), а (13) - в (2.2.1). .(2.3.15)
.(2.3.15)
 . Если принять в (11) x0(t)=d(t) и соответственно
. Если принять в (11) x0(t)=d(t) и соответственно  , то согласно (14)
, то согласно (14) (2.3.16)
(2.3.16) .(2.3.17)
.(2.3.17) .(2.4.1)
.(2.4.1) . При этом физический (реальный) сигнал x(t) является вещественной частью аналитического
. При этом физический (реальный) сигнал x(t) является вещественной частью аналитического  . Мнимая часть аналитического сигнала
. Мнимая часть аналитического сигнала  задается преобразованием Гильберта реального сигнала
задается преобразованием Гильберта реального сигнала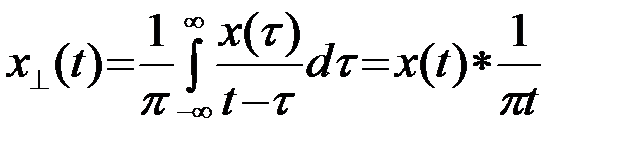 .(2.4.2)
.(2.4.2)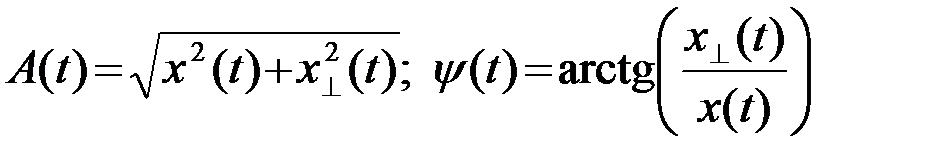 .(2.4.3)
.(2.4.3) (2.4.4)
(2.4.4) .(2.4.5)
.(2.4.5)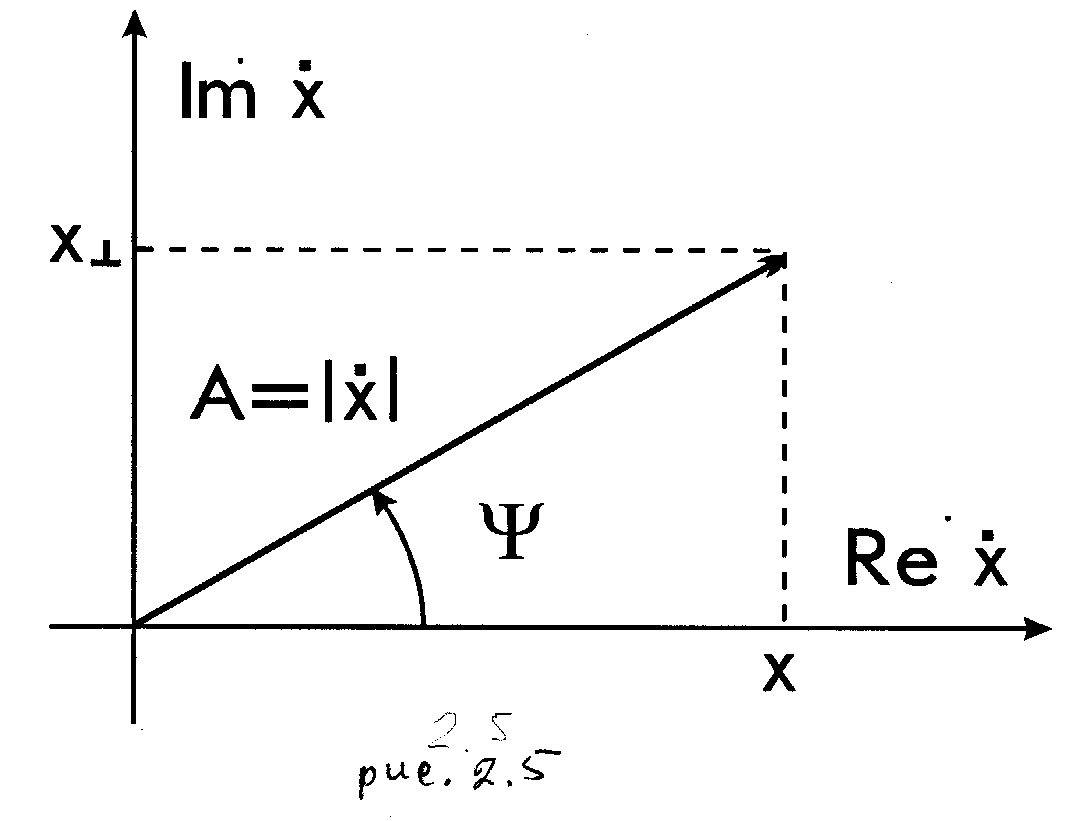
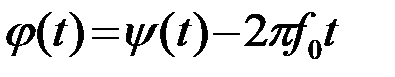 .(2.4.6)
.(2.4.6) (рис.2.5) выражаются при этом формулами: (1),
(рис.2.5) выражаются при этом формулами: (1), (2.4.7)
(2.4.7) , (2.4.8)
, (2.4.8)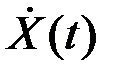 - комплексная огибающая сигнала
- комплексная огибающая сигнала .(2.4.9)
.(2.4.9) , называемые также квадратурными составляющими комплексной огибающей
, называемые также квадратурными составляющими комплексной огибающей  . Представление радиосигналов на комплексной плоскости (рис.2.5) широко используются при изучении модулированных сигналов (АМ, ФМ, ЧМ).
. Представление радиосигналов на комплексной плоскости (рис.2.5) широко используются при изучении модулированных сигналов (АМ, ФМ, ЧМ). {x(t)} (точнее его модуль |gx(f)|) имеет вид, изображенный на рис.2.6а.
{x(t)} (точнее его модуль |gx(f)|) имеет вид, изображенный на рис.2.6а.
 .
. .(2.4.10)
.(2.4.10) совпадает с
совпадает с  , изображенным на рис. 2.6а.
, изображенным на рис. 2.6а. .(2.6.11)
.(2.6.11) .(2.6.12)
.(2.6.12) .(2.6.13)
.(2.6.13)
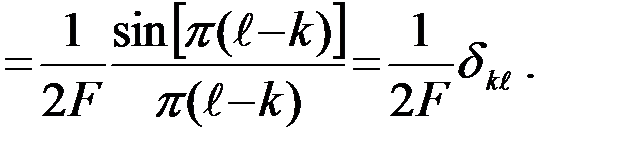 (2.6.14 )
(2.6.14 ) , функции отсчета обладают фильтрующим свойством
, функции отсчета обладают фильтрующим свойством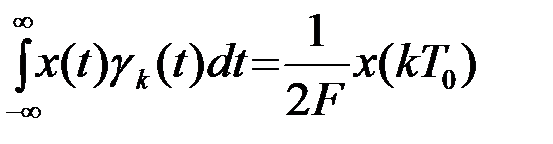 , (2.6.15)
, (2.6.15) (2.6.16)
(2.6.16) .(2.6.17)
.(2.6.17) . Соответствующая импульсная характеристика h Ф (t) фильтра, равная нулевой функции отсчета, будет
. Соответствующая импульсная характеристика h Ф (t) фильтра, равная нулевой функции отсчета, будет и
и 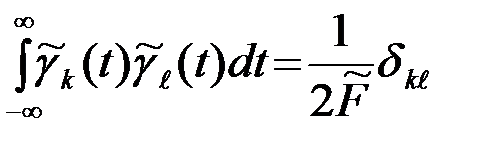 .
.
 .(2.6.18)
.(2.6.18)
 .(2.6.19)
.(2.6.19) (2.6.20)
(2.6.20) , (2.6.21)
, (2.6.21) .(2.6.22)
.(2.6.22) не совпадет со спектром исходного сигнала x( t). Формальное применение теоремы отсчетов к рассматриваемому случаю дает для периода дискретизации неоправданно малую величину
не совпадет со спектром исходного сигнала x( t). Формальное применение теоремы отсчетов к рассматриваемому случаю дает для периода дискретизации неоправданно малую величину  .
. с последующим выделением после дискретизации вещественной части
с последующим выделением после дискретизации вещественной части  . Так как спектр аналитического сигнала отличен от нуля только в полосе fÎ(f0-F, f0+F) (рис.2.6), рассуждения и преобразования при выводе формулы дискретизации аналитического сигнала
. Так как спектр аналитического сигнала отличен от нуля только в полосе fÎ(f0-F, f0+F) (рис.2.6), рассуждения и преобразования при выводе формулы дискретизации аналитического сигнала  не отличаются от приведенных в основной теореме. При дискретизации сигнала
не отличаются от приведенных в основной теореме. При дискретизации сигнала  с периодом T0=1/2F периодически повторяющиеся спектральные полосы не перекрываются. Поэтому исходный сигнал
с периодом T0=1/2F периодически повторяющиеся спектральные полосы не перекрываются. Поэтому исходный сигнал  может быть восстановлен из дискретизированного
может быть восстановлен из дискретизированного  пропусканием последнего через фильтр с частотной характеристикой
пропусканием последнего через фильтр с частотной характеристикой (2.6.23)
(2.6.23) .(2.6.24)
.(2.6.24) , (2.6.25)
, (2.6.25)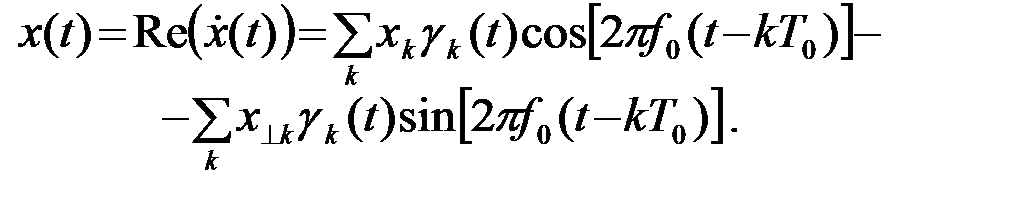 (2.6.26)
(2.6.26) . Если
. Если  удовлетворяет условиям теоремы отсчетов
удовлетворяет условиям теоремы отсчетов  при | f| > F, то
при | f| > F, то .(2.6.27)
.(2.6.27) равноценна обработке с использованием комплексной огибающей
равноценна обработке с использованием комплексной огибающей  . С практической точки зрения последняя предпочтительней. Значительно легче точно отсчитать мгновенные значения низкочастотных процессов Xc(t) и Xs(t), чем высокочастотных x(t) и x^(t), так как уменьшается требуемая точность фиксации отсчетных моментов t=kT0.
. С практической точки зрения последняя предпочтительней. Значительно легче точно отсчитать мгновенные значения низкочастотных процессов Xc(t) и Xs(t), чем высокочастотных x(t) и x^(t), так как уменьшается требуемая точность фиксации отсчетных моментов t=kT0.
 , где xk, yk Î R, k=1,...,n.
, где xk, yk Î R, k=1,...,n.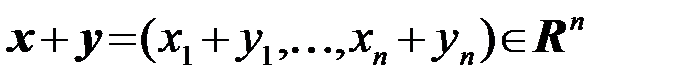 , (2.7.1)
, (2.7.1) , (2.7.2)
, (2.7.2) .(2.7.3)
.(2.7.3)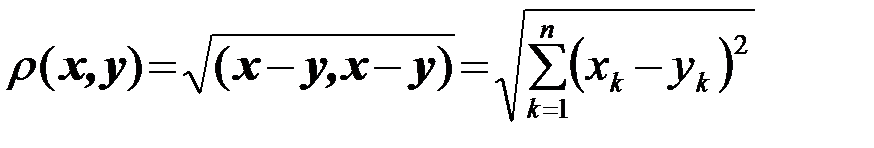 , (2.7.4)
, (2.7.4) (2.7.5)
(2.7.5) между векторами x и y
между векторами x и y . (2.7.6)
. (2.7.6) .(2.7.7)
.(2.7.7) , (2.7.8)
, (2.7.8) .(2.7.9)
.(2.7.9) .(2.7.10)
.(2.7.10) ,
, .(2.7.11)
.(2.7.11) базис пространства H, то любой элемент x=x(t) пространства H можно представить рядом (вместо k=0, ±1, ±2,... может быть другая бесконечная последовательность, например, k=0, 1, 2,...)
базис пространства H, то любой элемент x=x(t) пространства H можно представить рядом (вместо k=0, ±1, ±2,... может быть другая бесконечная последовательность, например, k=0, 1, 2,...) , (2.7.12)
, (2.7.12) ,
, . (2.7.13)
. (2.7.13) . Важно, что представление посредством ряда (12) устанавливает тождественность функции x(t), заданной на конечном или бесконечном интервале T, с дискретной последовательностью - вектором x =(..x-1, x0, x1,..) и, следовательно, возможность замены аналогового сигнала {x(t), tÎT} дискретным x ={xi, i=0, ±1, ±2,..}. Выбор базиса определяется соображениями удобства. Достоинством ряда Котельникова (базиса {gk}) применительно к сигналам с ограниченным спектром является простота определения коэффициентов ряда xk (компонент вектора x), равных мгновенным значениям x(kT0) сигнала x(t).
. Важно, что представление посредством ряда (12) устанавливает тождественность функции x(t), заданной на конечном или бесконечном интервале T, с дискретной последовательностью - вектором x =(..x-1, x0, x1,..) и, следовательно, возможность замены аналогового сигнала {x(t), tÎT} дискретным x ={xi, i=0, ±1, ±2,..}. Выбор базиса определяется соображениями удобства. Достоинством ряда Котельникова (базиса {gk}) применительно к сигналам с ограниченным спектром является простота определения коэффициентов ряда xk (компонент вектора x), равных мгновенным значениям x(kT0) сигнала x(t). (2.7.14)
(2.7.14) (2.7.15)
(2.7.15)


