

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Интересное:
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Пользуясь ЛЧХ, по номограмме (рис. 11) может быть определена вещественная частотная характеристика замкнутой системы.


Рис. 11. Номограмма для определения вещественной частотной характеристики замкнутой системы
Известны и алгебраические приемы, позволяющие сравнительно просто с достаточной точностью построить вещественную частотную характеристику (ВЧХ) замкнутой системы [5]. Для этого используется передаточная функция замкнутой системы, для статической системы с передаточной функцией (13)
 , (14)
, (14)
где  – коэффициент усиления разомкнутой системы.
– коэффициент усиления разомкнутой системы.
Ее частотная характеристика имеет следующий вид:
 . (15)
. (15)
После соответствующих преобразований

и, выделив действительную часть, получим выражение для вещественной частотной характеристики (ВЧХ) замкнутой системы
 (16)
(16)
Она позволяет оценить качество системы по характеристикам переходного процесса. Для рассматриваемого примера статической системы с передаточной функцией (13) и Кр =12 ВЧХ представлена на рис. 12.
|
|

Рис. 12. Вещественная частотная характеристика исходной замкнутой схемы
С ее помощью осуществляется оценка показателей качества переходного процесса: перерегулирования и длительности переходного процесса
 ;
;  , (17)
, (17)
где Р 0 – значение ВЧХ при w=0; Р max, wC – максимальная высота и частота основания низкочастотной трапеции ВЧХ. В данном случае Р max=1.22, wC=28с-1.
Таким образом, для рассматриваемого примера перерегулирование s=40% и длительности переходного процесса 0,12<tпп<0.45. На этапе анализа исходной САР такой точности оценки ее качества, как правило, бывает достаточно.
В тех случаях когда порядок системы не превышает 3-х и передаточная функция не имеет нулей, то достаточно эффективным средством оценки устойчивости и качества САР являются диаграммы Вышнеградского, которые позволяют с наименьшими затратами провести анализ таких систем.
|
|
Для астатических систем с типовым наклоном логарифмической амплитудно-частотной характеристики (ЛАЧХ) эффективным является применение номограмм качества, которые широко используются в инженерной практике.
Оценка точности САР от суммарного действия управляющих и возмущающих воздействий в установившемся режиме широко освещена в литературе [1-5].
Величина ошибок в установившемся режиме зависит от характера входных воздействий, порядка астатизма системы, ее коэффициента усиления и наибольшей постоянной времени. Таким образом, качество установившегося режима работы определяется параметрами низкочастотной части ЛАЧХ. Для того чтобы максимальные ошибки, возникающие в синтезируемой системе, не превышали заданных допустимых значений, необходимо правильно выбирать параметры низкочастотной части желаемой ЛАЧХ. В общем случае структурная схема любой САР, на которую действует входное воздействие u (t) и возмущение f (t), может быть представлена в виде схемы, показанной на рис. 13.

Рис. 13. Структурная схема системы автоматического регулирования
В этом случае изображение сигнала ошибки будет иметь следующий вид:
 , (18)
, (18)
где  - передаточная функция разомкнутой системы по задающему воздействию u (t);
- передаточная функция разомкнутой системы по задающему воздействию u (t);  – передаточная функция разомкнутой системы по возмущающему воздействию f (t).
– передаточная функция разомкнутой системы по возмущающему воздействию f (t).
В статическом режиме все воздействия постоянны во времени. Полагая 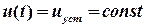 и
и 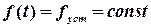 , получаем выражение установившейся ошибки
, получаем выражение установившейся ошибки
 . (19)
. (19)
Если передаточная функция W PU (p) содержит v интеграторов, а W F (p) имеет k интеграторов, то система обладает астатизмом v -го порядка по задающему воздействию и (v-k)-го порядка по возмущающему воздействию.
При v = k статическая ошибка равна нулю, то есть система является астатической по возмущающему и задающему воздействиям. Когда хотя бы одно из воздействий меняется с постоянной скоростью или постоянным ускорением, то возникает динамический установившийся режим.
|
|
Например, при  и
и 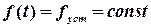 установившаяся динамическая ошибка
установившаяся динамическая ошибка
 . (20)
. (20)
Если  и
и 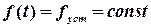 , то
, то
 . (21)
. (21)
При гармоническом входном воздействии (например, качке) возникает вынужденный установившийся гармонический режим работы. В этом режиме при  и
и 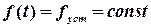 ошибка будет иметь вид:
ошибка будет иметь вид:

 ;
;  , (22)
, (22)
где e max - амплитудное значение ошибки; j- фаза сигнала ошибки.
При оформлении данного этапа КУРСОВОГО ПРОЕКТА необходимо:
–дать аргументированное обоснование выбора метода анализа;
–привести необходимые выкладки при исследовании устойчивости и оценке точности САР в установившемся режиме;
–произвести сравнительную оценку качества исходной САР с требуемыми показателями.
|
|
|

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!