Часть 2. О принципах кратчайшего времени и наименьшего действия

Юдин С. Ю. [email protected]

Как и обещано в статье, посвящённой двум мерам механической формы движения материи, чтобы завершить вопрос о двух мерах, рассмотрим, какое отношение имеет к этому вопросу такая физическая величина, как “действие”. Почему же такая величина, как “действие” претендует на роль ещё одной меры механического движения? И вот здесь получается просто «замкнутый круг». Претендует она потому, что среди множества различных вариационных принципов есть и такой, как принцип наименьшего действия, а он в свою очередь выделился из общей толпы различных величин, оптимизируемых при различных вариационных принципах потому, что есть квант действия, да ещё и имеющий официальный статус наименьшего действия в Природе - назвали эту величину (постоянную Планка) квантом действия, т.е. отмеренной порцией механического движения. Произошло это потому, что размерность этой величины совпала с размерностью величины, которую надо минимизировать в принципе наименьшего действия (и там, и там джоуль умножить на секунду), а не с какой-то другой величиной - например, с величиной наименьшего принуждения, которую надо минимизировать в принципе Гаусса и которая имеет размерность джоуль разделить на секунду в квадрате (впрочем, физический смысл и этой величины так же непонятен, как и первой). Давайте постараемся всё же отделить действие от кванта действия и рассмотреть обе этих величины, исходя не из их размерности, а из их физического смысла.

И начнём рассмотрение принципа наименьшего действия с того, что само название этого принципа как наименьшего действия неудачное, на что указывали все, кто занимался его разработкой (Эйлер, Лагранж и другие), так как, во-первых, величина действия при соблюдении этого принципа может быть не только минимальной, но и максимальной, т.е. имеет место не просто минимум, а экстремум функции, а во-вторых, само понятие “действия” не имеет никакого отношения не только к кванту действия как к какой-то минимальной величине, но и вообще к “действию” как таковому, т.е. к взаимодействию между телами. Поэтому с таким же успехом его можно было бы назвать принципом наименьшего зла, наименьших потрясений или наибольшей влюбленности, а уже исходя из того, что конкретный автор хочет получить, используя этот принцип, он и наполнял бы содержанием понятие зла, влюблённости или потрясений. И вообще, складывается такое впечатление, что каждый автор, излагая свой вариант этого принципа, как бы предлагает вам сыграть в карты, а после окончания игры, исходя из того что получилось, объявляет вам, что он выиграл, потому что мы играли в очко; или при другом раскладе всё равно говорит, что он выиграл, потому что мы играли в дурака.

А такое название этот принцип получил ещё в 1744 году, когда ещё даже не существовало таких понятий, как энергия, мощность и т.д., и именно исходя из того, что подразумевалось достижение какой-то цели - как, например, при игре в карты, а не исходя из физического смысла. Мопертюи дал это название, исходя из метафизических представлений о природе, где всё должно происходить из каких-то разумных соображений, как будто природа в своих действиях преследует какие-то цели, которые сама перед собою и ставит - т.е. имеется в виду наличие Бога, который осуществляет в природе только разумные процессы. А ведь, кроме разумности поведения, в этом принципе действительное движение в конкретное время приходится рассчитывать с помощью будущего движения, т.е. получается, что настоящее зависит от будущего, а следовательно, без божественного предвидения здесь никак не обойтись. Уже позже в этот принцип принесли математическое содержание великие геометры (читай математики) Эйлер и Лагранж, а затем и Гамильтон, но божественное начало так и продолжает витать над этим принципом. Правда, многие учёные отвергают божественное начало в этом принципе, но как-то не очень убедительно. Вот, например, Планк [5], который, естественно, после своего кванта действия просто обязан боготворить этот принцип, уже в ХХ веке пишет о его сущности так: “В связи с этим надо вспомнить о Теодице Лейбница, в которой выдвинут тезис о том, что истинным миром среди всех миров, которые могли бы быть сотворены, является тот мир, который наряду с неизбежным злом содержит в себе максимум добра. А этот тезис является ничем иным, как вариационным принципом, выраженным в такой же форме, как возникший позднее принцип наименьшего действия. Неизбежное сцепление добра и зла играет при этом роль предписанных условий, и ясно, что фактически из этого тезиса могли бы быть выведены все особенности действительного мира, если бы удалось математически точно сформулировать, с одной стороны, меру для количества добра, а с другой стороны – предписанные условия”. Я извиняюсь за такую длинную цитату, но вопрос действительно очень серьёзный, т.к. с помощью принципа наименьшего действия и сейчас пытаются получить “все особенности действительного мира”. Вначале этот принцип стараниями Гельмгольца перебрался из механики в термодинамику, а сейчас уже и в квантовую механику, и в биологию, и в экономику.

По молодости и Эйлер, величайший геометр всех времён и народов, который и заложил математические основы в этот принцип (рискну предположить, что и основы Русской математической школы), тоже придавал ему теологическое значение и очень много уделял ему внимания, но со временем его энтузиазм иссяк и он, также как и Лагранж, отвергал претензии этого принципа на всеобщую значимость и на звание основного общего закона природы. Но вот, например, уже в современном цитатнике [3] (считайте, официальном учебнике СССР, а теперь России) этот принцип именно основным законом Природы и объявляется, хотя я думаю, что это уже наверное больше относится не к науке, а к политике - ведь, как я уже указывал в предыдущей статье на примере с лагранжианом, главный проповедник этого принципа Ландау из коньюктурных соображений очень быстро меняет свои научные взгляды, исходя из “официальной” точки зрения в науке. И хотя формально вроде бы все современные ученые отвергают существование Бога, но используя этот принцип, они официально вносят Его в науку.

Да, история у этого принципа громкая (даже Вольтер руку приложил, как писатель), и исторически его идея была первой в ряду многих вариационных принципов, но вот практической пользы от него оказалось ещё меньше, чем от уравнений Лагранжа 2-го рода, возможности которых рассмотрены мною в [9]. Например, Пуассон назвал его “лишь бесполезным правилом”, а Планк писал, что он “не оказал никакого существенного практического влияния на научный прогресс” [5] (как Вы поняли, это высказывание конечно же относилось к прогрессу до появления его кванта действия).

Но попробуем всё же разобраться как в сущности самого принципа наименьшего действия, так и самой оптимизируемой величины, т.е. действия. Впервые похожая на этот принцип идея, использованная в принципе кратчайшего времени движения света, была высказана ещё Ферма [8] в 1662 г., а позже в 1682 г. и Лейбницем, исходя из коэффициента преломления света (это вообще удивительно, т.к. о природе света тогда было ещё более смутное представление, чем о законах механики). Тем ни менее, эта идея кратчайшего времени Ферма натолкнула И. Бернулли [2] в 1696 г., исходя только из этого голого принципа кратчайшего времени движения, на аналогичное решение задачи для движения механических тел в поле тяжести Земли - и что самое удивительное, так это то, что у него всё очень удачно получилось. К сожалению, задача Ферма решена геометрически, а в решении Бернулли хотя уже и используется дифференциальное исчисление, основы которого незадолго до этого заложили Лейбниц и Ньютон, но это решение сейчас тоже трудно воспринимается, т.к. тогда даже координатные оси располагались не так, как сейчас. На всякий случай напомню, что все задачи тогда решались геометрически - например, Ньютон в своих Началах, которые были написаны примерно в это же время, все задачи решал именно так, да и сама алгебраическая запись уравнений (причём самые её начала) была введена Виетом только за 100 лет до этого. Поэтому решение задачи Бернулли я дам в сокращении и в современных терминах, а современное математическое решение задачи Ферма приведу из работы [1].

На Рис.1 представлена задача о наименьшем времени Ферма, в которой доказывается, что луч света при движении сразу в двух средах с разным сопротивлением движению, которые на рисунке разделены горизонтальной линией (ось x) - например, из воздуха в воду, - пройдет не по прямой ACB, соединяющей две точки A и B, а по линии ADB, потому что время движения при этом будет минимальным. При этом отношение синусов углов alfa1 к alfa2 будет равно коэффициенту преломления между этими средами, т.е. отношению скоростей света в этих двух средах, которые можно считать величиной пропорциональной разряженности вещества. В качестве постулата при решении этой задачи Ферма принял, что Природа действует наиболее лёгкими и доступными путями и, исходя из этого, он доказывает, что наиболее лёгким путем, выйдя из точки A, свет достигнет точки B, если будет двигаться по пути ADB, т.к. при этом он затратит на это минимальное время – а следовательно, это и будет истинный путь света.

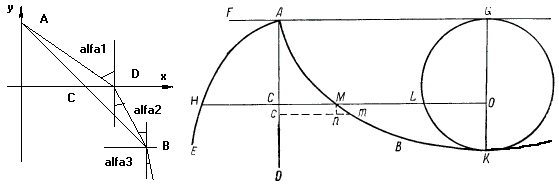
Рис.1 Задача кратчайшего времени движения луча света.

Рис.2. Задача кратчаишего времени движения тела в поле тяжести Земли.

Если у нас градиент скорости по оси x не будет изменяться, то мы легко найдём закон движения луча, чтобы он за минимальное время достиг точки B – как прямую. Исходя из геометрических соображений и зная скорость луча над осью абсцисс V1 и под ней V2, найдём общее время движения луча:

t = sqr(Ya^2+Xc^2)/V1 + sqr(Yb^2+(Xb-Xc)^2)/V2

Теперь возьмём производную dt/dx и приравняем её нулю, откуда получим:

sin(alfa1)/V1 = sin(alfa2)/V2

Это есть ничто иное, как закон преломления Снелиуса, только записанный в другой форме, где V1 = c/n1, V2 = c/n2 , c - скорость света в вакууме, n1 и n2 - абсолютные показатели преломления среды относительно вакуума. Тогда можно записать:

sin(alfa1)/sin(alfa2) = n2/n1 = n21

Здесь n21 – это привычное нам значение показателя преломления второй среды относительно первой. Если мы ниже точки B расположим третий слой среды с коэффициентом преломления n3, т.е. скоростью движения света в нём V3, то аналогично можно записать:

sin(alfa2)/V2 = sin(alfa3)/V3

Таким образом, мы видим, что для минимального времени движения луча света, переходящего последовательно из среды с одним коэффициентом преломления в среду с другим коэффициентом преломления, достаточно, чтобы соблюдался закон преломления Снелиуса - а он, естественно, будет соблюдаться, если не считать случая, когда происходит полное отражение света от одной из сред (при переходе из более плотной среды в менее плотную под большим углом). При этом, как Вы заметили, у нас отношение синуса угла преломления к скорости света в каждой среде всегда остаётся одним и тем же, т.е. константа.

Это соотношение и применил Бернулли для решения своей задачи. На Рис.2 представлен подлинник его рисунка к этой задаче, где надо найти вид кривой AMK, по которой должн двигаться луч света, чтобы за минимальное время пройти от точки A к точке K в слоистой среде. При этом слои среды располагаются параллельно линии AG, т.е. оси абсцисс, а плотность среды убывает сверху вниз вдоль оси ординат AD по произвольному закону с изменением скорости движения луча при уменьшении высоты (кривая AHE), т.е. увеличении ординаты. При ординате AC скорость равна HC. Выделяя элемент кривой ds (на рисунке отрезок Mm) и исходя из того, что отношение синуса угла преломления к скорости движения луча должно быть на всем пути постоянным, т.е. равным какой-то постоянной величине 1/a - Бернулли записал это как (dx/ds)/V = 1/a, что можно переписать a*dx = V*ds. Если левую и правую части возвести в квадрат и заменить ds^2 на dx^2 + dy^2, то получится общее дифференциальное уравнение:

dx = V*dy/sqr(a^2-V^2)

Это и есть уравнение движения луча света за минимальное время при заданном законе изменения скорости или коэффициента преломления в вертикальных слоях при заданной начальной скорости, которая вообще-то должна быть отличной от нуля, в отличии от закона изменения, заданного Бернулли. Здесь луч достигает точки K и вылетает из A - если закон изменения скорости света будет таким, что мы получим циклоиду. Если в точке K луч света ещё и отразится, то он сможет пройти и вторую половину дуги циклоиды. Но об этом позже, а сейчас давайте проведём аналогию с движением материальной точки в такой среде.

При этом точка может скользить по направляющей произвольной формы без трения и механического сопротивления среды (в смысле, при отсутствии сопротивления воздуха), а с увеличением ординаты (в координатах рисунка) скорость падающих тел будет увеличиваеться - мы можем это интерпретировать как уменьшение плотности в слоях нашей гипотетической среды. Взяв полученный Галилеем закон изменения скорости падающих тел в поле тяжести Земли, Бернулли подставил в свою формулу полученное из закона Галилея значение скорости V = sqr (a*Y) и окончательно получил уравнение циклоиды:

dx = dy * sqr ( y / ( a – y ))

Т.е. получается, что у нас механическая задача решена с помощью законов оптики, а следовательно, законы механики и оптики в своей основе похожи и имеют какие-то общие закономерности. Поэтому решение этой задачи после задачи Ферма с использованием критерия оптимизации укрепило веру многих учёных того времени в то, что все законы Природы действуют так, чтобы все процессы происходили с достижением какой-то цели. Если Вы ещё не представили себе значение этих двух задач для учёных того времени, то это примерно равноценно открытию ядерных реакций или гена человека в наше время, притом учёные того времени видели в этих решениях филосовский камень для открытия всех законов Природы, которые обязательно должны были действовать так, чтобы достичь какой-то цели и надо было только найти критерии, по которым Природа определяет достижение своей цели - т.е. как писал Планк в приведенной выше цитате, “надо математически точно сформулировать меру для количества добра”.

Надо сказать, что в то время, когда математика только становилась на ноги, вариационные принципы в механике развивались очень бурно, поэтому не изобрести что-нибудь новенькое в математическом плане тогда не мог только ленивый. Правда, все эти вариационные принципы являются ближайшими родственниками основного уравнения динамики, т.е. дифференциального вариационного принципа Даламбера-Лагранжа, и получены в основном только для консервативных систем, когда полная энергия в начальной и конечной точках движения системы равны, т.е. в них обязательно используется энергия как мера механической формы движения материи и при этом обязательно должен соблюдаться закон её сохранения. Но теперь на вариационные интегральные принципы стали возлагать ещё большие надежды и увидели в них не просто очередной закон Природы, а закон над законами, т.е. инструмент который позволит получить все остальные законы. Но с применением принципа наименьшего действия возникла одна очень большая проблема - а именно, трудность в “математической формулировке меры для количества добра”. Наиболее известны формулировки Мопертюи-Лагранжа и Гамильтона-Якоби: в первом случае критерий оптимизации вычисляется как интеграл по пути от произведения массы на скорость, т.е. количества движения, а во втором - как интеграл по времени от лагранжиана, т.е. разности кинетической и потенциальной энергий системы. Как в одном, так и в другом случае размерность критерия получается джоуль умножить на секунду, но физический смысл как мы видим здесь совершенно разный, и как раз физический смысл всех этих изобретаемых критериев оптимизации никак никому и не удалось понять.

Для Лагранжа, например, физический смысл принципа наименьшего действия заключался именно в конкретизации закона живых сил (читай закона сохранения энергии), и он даже писал: “его можно было бы с большим основанием назвать принципом наибольшей или наименьшей живой силы” [6], а Лаплас о механическом содержании этого принципа говорил так: “интеграл живой силы системы, умноженный на элемент времени, есть минимум, а следовательно, истинная экономия природы есть экономия живой силы” [6]. Но, как мне кажется, ближе всех к сущности этого принципа подошел Эддингтон, который очень остроумно заметил, что принцип наименьшего действия можно сравнить с утверждением: “если бы законы арифметики перестали быть верными, то 2+2 было бы больше или равно (но, наверное, не меньше) четырём” [6]. Забегая вперед, скажу, что, как будет показано далее, возможны случаи, когда будет и меньше четырех - иначе говоря, если бы законы механики перестали быть верными, то в каком-то приближении для некоторых случаев можно было бы воспользоваться принципом наименьшего действия.

Но прежде чем перейти к экспериментальной проверке принципа наименьшего действия на предмет “математической формулировки меры для количества добра”, давайте более подробно посмотрим, насколько верны полученные нами решения задач Ферма и Бернулли с физической точки зрения. И для начала просто посмотрим, как будет двигаться луч света в слоистой среде, для которой мы и решали наши задачи. На рис.3 и 4 изображено графическое окно программы Hrono1, которую можно скачать с моей домашней страницы http://ser.t-k.ru/, где мы видим 20 горизонтальных прозрачных слоев, расположенных через 1 метр с разными коэффициентами преломления, численные значения которых даны слева в виде гистограммы. Смоделированный луч света при проведении вычислительного эксперимента вылетает из левого верхнего угла и движется по 20-му (верхнему) слою до точки в начале 19-го слоя, абсциссу которой мы задаём, и далее уже в соответствии с законом преломления света. На рис. 3 плотность среды увеличивается, а на рис.4 уменьшается от верхних слоев к нижним по квадратичной зависимости. Аналогичная картина будет наблюдаться и при линейной зависимости на рис.5 и 6.

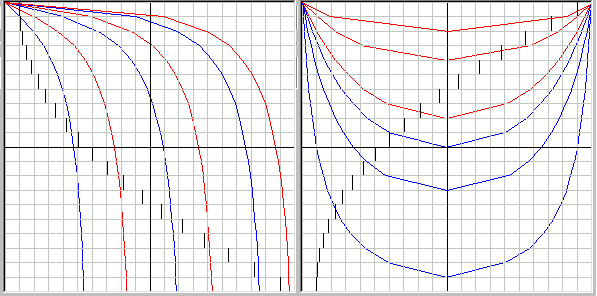
Рис.3 Движение луча света, когда коэффициент преломления изменяется по слоям по квадратичной зависимости и увеличивается сверху вниз.

Рис.4 Движение луча света, когда коэффициент преломления изменяется по слоям по квадратичной зависимости и увеличивается снизу вверх.

Честно говоря, мне эти кривые мало напоминают циклоиды, только первые две кривые на рис.3 очень похожи на циклоиды (начальный участок остальных сильно искажен из-за большой толщины первого слоя). Если принять, что это циклоиды, то при радиусе образующего круга 3…4 метра получается, что циклоида должна достичь точки K на рис. 2 на 9…12 слое, т.е. через расстояние AG = pi*R, а далее луч света должен начать отклоняться влево, хотя в эксперименте мы этого не наблюдаем. Более того, чтобы луч света стал двигаться строго вертикально, необходимо, чтобы скорость света была близка к нулю, т.к. только тогда будет соблюдаться соотношение sin (alfa1) / V1 = sin (alfa2) / V2 и, следовательно, в это соотношение надо внести какие-то поправки. Но самое интересное - это то, что, как видно из рис. 5, оказывается, луч света в одну и ту же точку пространства (там, где пересекутся лучи, вылетевшие из одной точки) может придти разными путями! Это происходит, если он движется из более плотных слоев в менее плотные, т.к. в какой-то момент он вынужден будет отразиться от одного из слоев и изменить градиент своей скорости, т.е. направление движения поперёк слоев (вдоль слоёв градиент измениться не может). А это отражение произойдёт в тот момент, когда при большом угле падения получится, что синус угла преломления окажется больше единицы – естественно, этого не может быть, поэтому свет просто полностью отразиться от этого слоя как от зеркала, изменив градиент своей скорости. Таким образом, возможно, что свет не всегда затрачивает минимум времени, чтобы из одной точки пространства попасть в другую, а значит, принцип кратчайшего времени Ферма будет справедлив не всегда, а только когда мы рассматриваем небольшие участки движения, где градиент скорости не меняет своего направления!

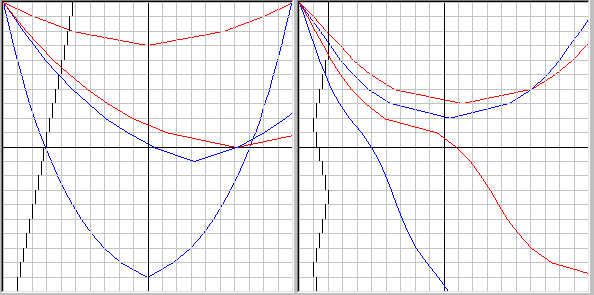
Рис.5 Движение луча света, когда коэффициент преломления изменяется по слоям по линейной зависимости и увеличивается снизу вверх.

Рис.6 Движение луча света, когда коэффициент преломления изменяется по слоям по произвольной зависимости.

Примем для простоты расчётов, что скорость света в вакууме равна 1 м/с, а т.к. она обратно пропорциональна коэффициенту преломления слоя, то например в слое, где коэффициент преломления будет равен 2, скорость света будет 0,5 м/с. В этом случае время движения по дальнему пути (синяя линия в средней части рис.5) до точки пересечения с соседним красным лучом будет 72,67 сек., что больше, чем по более короткому пути (красный луч) - 71,9 сек., что вполне естественно и не вызывает вопросов. Но если мы рассмотрим аналогичный случай, показанный на рис.6, то выяснится, что время движения луча по дальнему пути (синяя линия в верхней части рисунка) составляет 29,82 сек., что даже меньше, чем время движения по ближнему пути (красная линия) - 30,41 сек., т.е. мы получили результат, противоположный предыдущему опыту! А если посмотреть ещё и на две нижние траектории движения света, то видно, что траектория движения при различных условиях может быть очень сложной. Таким образом, свет не только может попасть из одной точки пространства в другую разными путями, но даже нельзя заранее сказать, при движении по какому из множества возможных путей - более короткому или более длинному - он достигнет этой точки за минимальное время! А следовательно, принцип кратчайшего времени является только частным случаем общего закона движения света, который имеет место на ограниченном пространстве только в том случае, когда свет не меняет градиента своей скорости.

Но тогда, может быть, это относится и к механическому движению, и тогда весь принцип наименьшего действия с его критериями оптимизации не имеет никакого отношения к науке, а является чистой метафизикой? Воспользуемся опять программой Hrono1 и смоделируем движение груза массой 1 кг в поле тяжести Земли по различным траекториям (1 - прямая линия, 2 - циклоида, 3 - парабола и 4 - дуга окружности), при этом трением скольжения груза по этим направляющим пренебрегаем (более подробно о том, как это происходит, можно прочитать в описании программы). Причём траектории движения могут быть как начинающимися с нулевой точки, когда в начальный момент они параллельны оси ординат (будем называть их нулевыми), так и начинающиеся с произвольного момента, когда движение начинается не строго вертикально (будем называть их произвольными). На рис. 7 показаны возможные траектории движения груза из начальной точки с координатами Xn = -9м и Yn = 9м в конечную точку с координатами Xk = 9м и Yk = -2,455м (начало координат находится в центре рисунка). Ордината конечной точки выбрана таким образом, чтобы угол поворота круга, образующего циклоиду при качении без скольжения по линии, параллельной оси абсцисс, был равен 3,14 радиана, т.е. чтобы у нас получилась ровно половина циклоиды (синяя линия). Если угол fiK будет меньше 3,14, то мы получим произвольную циклоиду с заданным fiK, т.е. только часть первой половины циклоиды. Точно также мы можем получить нулевую дугу окружности и произвольную, задав абсциссу центра окружности X40 (красные линии). При задании направляющих в виде параболы (жёлто-зелёные линии) мы для нулевой параболы задаём закон её изменения X3 = X30 + K3 * (Y30 - Y3) ^2, где X30 = Xn и Y30 = Yn, а коэффициент K3 вычисляется. Для произвольной параболы задаётся X30 в законе вычисления её ординат Y3 = Y30 + K3 * (X30 - X3) ^2, а остальные параметры вычисляются.

Но прежде чем начать проведение вычислительных экспериментов, проверим, насколько грамотно мы составили математическую модель, на основе которой будут проводиться вычислительные эксперименты, и насколько удачно мы задали параметры для численного решения - например, шаг решения или жёсткость направляющей. Для этого сравним несколько показателей полученных аналитически, с этими же показателями полученными с помощью вычислительного эксперимента при шаге решения 0,005 сек. Сравним, например, длину пути по прямой и по дуге окружности 21,34 и 25,39 метра - теория, и соответственно 21,37 и 25,45 – эксперимент, или время движения по прямой 2,848 сек. – теория, и 2,850 – эксперимент, или суммарную энергию тела в начальной и конечных точках движения при проведении эксперимента E01=88,154 и E1=88,154, E02=88,19 и E2=88,13, E03=88,188 и E3=88,183, E04=88,19 и E4=88,19 Дж. Полученные данные позволяют сделать вывод, что математическая модель адекватно описывает поведение нашей системы, а заданные нами параметры системы обеспечивают необходимую нам точность.

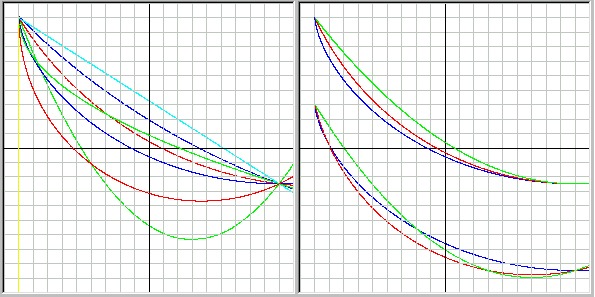
Рис.7. Возможные траектории движения тела в поле тяжести Земли.

Рис.8 Движение тела по траекториям близким к нулевой циклоиде.

Как и следовало ожидать, по экспериментальным данным (при шаге решения 0,002 сек) время движения по нулевой циклоиде t2 (0) = 2,406 сек. оказалось минимальным (здесь и далее индекс 2 опять относится к циклоиде, 1 - к прямой линии, 3 - к параболе и 4 - к дуге окружности, а в скобках указывается, нулевая это траектория или произвольная). Для сравнения привожу результаты по другим траекториям: t1 = 2,850 сек, t2 (fiK = 2,416) = 2,598 сек, t3 (0) = 2,428 сек, t3 (X30 = 3) = 2,602 сек, t4 (0) = 2,468 сек, t4 (X40 = 12) = 2,470 сек. Правда, этот результат справедлив только для консервативных систем, т.е. при отсутствии диссипации энергии, когда при движении груза на него не будет действовать сопротивление среды, но в программе предусмотрена возможность проведения эксперимента и с диссипацией, правда, только при линейной зависимости силы сопротивления от скорости движения. Например, при коэффициенте сопротивления Kj =1 время движения по вышеперечисленным траекториям будет следующее: t1= 5,052 сек, t2 (0) = 5,808 сек, t2 (fiK = 2,416) = 4,774 сек, t3 (0) = 4,990 сек, t3 (X30 = 3) = 4,908 сек, а движения t4 (0) и t4 (X40 = 12) вообще сошли с дистанции, т.к. не смогли преодолеть яму потенциальной энергии. Здесь в более выигрышном положении при прочих равных условиях оказываются траектории, где коэффициент вариации скорости при движении минимален - например, прямая, которая хоть и показала в этом забеге четвёртый результат, но при увеличении Kj обязательно займет первое место.

Теперь давайте проверим, нет ли каких-то кривых для идеальных систем, которые очень близко совпадают с циклоидой и у них время движения окажется меньше? Как показывают результаты экспериментов с различными параболами и дугами окружности на рис.8, как в тех случаях, когда кривые находятся выше циклоиды t3 (X30 = 9) = 2,506 сек и t4 (X40 = 9) = 2,432 сек, так и в тех случаях, когда кривые проходят ниже циклоиды t3 (X3 0= 6) = 2,474 сек и t4 (X40 = 6) = 2,418 сек, время движения по циклоиде всегда меньше.

Рис.9 Варианты движения тела в поле тяжести Земли, когда конечная точка траектории находится выше или ниже точки, получающейся при движении по половине полной нулевой циклоиды.

Рис.10 Несколько вариантов траекторий, направления движения по которым в начальной точке незначительно отличаются друг от друга.

А теперь посмотрим, не изменится ли результат, если конечную точку сместить выше или ниже. Как показывают результаты экспериментов на рис.9, и в этом случае время движения по циклоиде остается минимальным - как при сдвиге точки вверх (t2 (0) = 2,578 сек, t3 (0) = 2,928 сек и t4 (X40 = 2) = 2,608 сек), так и при сдвиге вниз (t2 (0) = 2,486 сек, t3 (0) = 2,490 сек и t4 (X40 = 15) = 2,494 сек). Таким образом высказывание Эддингтона о принципе наименьшего действия применительно к движению груза в поле тяжести Земли из одной точки в другую можно интерпретировать так, что время движения при этом будет быстрее всего или равно или больше времени движения по циклоиде.

Но вот если мы в начальный момент времени зададим нашему грузу какую-то начальную скорость, то здесь будет уже не всё так однозначно. Давайте возьмём несколько траекторий, которые в начальный момент расходятся под небольшими углами друг к другу, и зададим начальную скорость, направление которой совпадёт с начальным участком одной из них. Для траекторий, изображенных на рис.10, наихудший результат при начальной скорости равной нулю, как видно из таблицы 1, имеет прямая линия. Давайте теперь зададим различные значения начальной скорости, направление которой совпадет с траекторией прямой линии, и полученные результаты занесём в ту же таблицу - как видно, при небольшой скорости лучшие результаты у параболы и дуги за счёт более оптимальной траектории, но уже при средней скорости лучший результат у циклоиды, у которой траектория средней оптимальности, но угол отклонения от прямой меньше, чем у параболы и дуги; но при большой скорости лучшее время показывает прямая, хотя у неё самая неоптимальная траектория из четырех, и здесь главную роль играет уже начальная скорость. Таким образом, время движения груза по нулевой циклоиде будет всегда минимальным в поле тяжести Земли только в одном частном случае, когда начальная скорость равна нулю или её направление совпадает с начальным участком циклоиды. Ещё более запутанной становится ситуация, если при движении груза на него при наличии начальной скорости будет действовать сопротивление среды, т.е. у нас будет неконсервативная система, хотя в этом случае авторы этого принципа уже не претендуют на его применимость.

Табл.1

	V=0	V0=2,134	V0=10,67	V0=21,34
t1	2,850	2,472	1,470	0,902
t2(fiK=2,416)	2,596	2,312	1,462	0,920
t3(X30=9)	2,506	2,256	1,480	0,954
t4(X40=15)	2,506	2,260	1,484	0,954

Чтобы закончить с задачей Бернулли, нам осталось рассмотреть только случаи, когда напряженность силового поля, в котором движется груз, отличается от локального поля тяготения Земли, т.е. когда оно, например, изменяется в значительных интервалах в зависимости от расстояния между взаимодействующими телами, как в законах Ньютона или Кулона. И хотя мы именно в одном из таких полей и проводили наши вычислительные эксперименты, но разность как ординат, так и абсцисс в начальной и конечной точках движения груза была несоизмерима с расстоянием от груза до центра Земли, поэтому мы рассматривали движение груза практически в плоском постоянном поле, где его напряженность не меняется как при изменении ординаты, так и при изменении абсциссы, т.е. в любой точке на груз действовала почти постоянная сила m*g и при этом её вектор всегда был направлен почти вертикально вниз. Чтобы груз двигался действительно в сферическом поле, надо чтобы расстояние между начальной и конечной точками движения было соизмеримо с расстоянием до источника, создающего это поле. Здесь возможны два варианта: либо мы берём расстояния между точками, соизмеримые с расстоянием до Земли, либо оставляем точки на своих местах, а гравитационное поле заменяем электростатическим, которое может дать соизмеримые усилия при малых масштабах. Рассмотрим движение груза в электростатическом поле, когда наш груз и другое взаимодействующее с ним тело такой же массы, только жёстко прикрепленное к оси ординат инерциальной системы отсчета, зарядим их разноименными зарядами q1 = q2 = 0,0005 Кулона и разместим второе тело на оси ординат (также, как это было и с Землей) на расстоянии –10 м от оси абсцисс, что позволит получить время движения, соизмеримое с рассмотренными нами выше случаями. При этом влияние гравитационного поля Земли исключаем, задав массу второго тела равной 1 кг или вообще нулю. Итак, рассмотрим два варианта движения груза, как в обычном сферическом поле точечного заряда (будем обозначать его var2-, где 2- означает, что напряженность поля с ростом расстояния уменьшается во второй степени, рис.12), что является наиболее частым случаем, так и в плоском переменном поле с линейной обратной зависимостью от расстояния (будем обозначать это var1-, рис.11), когда, например, второй заряд (масса) равномерно распределён по горизонтальной линии, т.е. сила взаимодействия между телами изменяется с изменением ординаты, а направление действия силы остаётся постоянным (строго вниз). Вообще-то поле во втором случае будет строго var1- в том случае, если длинна этой линии будет равна бесконечности, но уже при длине этой линии как вправо так и влево от оси ординат на 10 размеров экрана и при её ординате –0,25 размера экрана ошибка, когда масса (заряд) 1 находится в верхней точке экрана, составит всего 0,28%.

При проведении этих экспериментов жёсткость груза увеличим в 10 раз, т.к. усилия в нижней точке параболы на порядок больше, чем в верхней как из-за увеличения силы притяжения между телами, так и из-за большой центробежной силы, что может на несколько сантиметров исказить траекторию движения при упругой деформации груза. Для наглядности, на рис.11-12 прямые коричневые линии показывают траектории свободного движения груза, т.е. не соединенного с направляющей, а в левом верхнем углу маленькая синяя линия отражает закон изменения напряжённости поля: если поле плоское, то нулевой уровень потенциальной энергии будет показан прямой линией совпадающей с осью абсцисс, а если сферическое - окружностью радиуса Rz вокруг 2-го груза. Согласно экспериментальным данным, при движении в поле var1- (t2 (0) = 1,998 сек, t3 (X30 = 5) = 2,036 сек, t4 (X40 = 5) = 1,984 сек) циклоида уже не является брахистохроной, а при движении в поле var2- (t2 (0) = 2,684 сек, t3 (X30 = 5) = 2,634 сек, t4 (X40 = 8) = 2,638 сек) получается, что время движения по циклоиде вообще самое большое. Т.е. циклоида в общем случае не является брахистохроной, что вполне естественно, т.к. уравнение циклоиды получено Бернулли из общего решения для очень частного случая, т.е. для плоского поля с постоянной напряженностью, а для других полей даже высказывание Эддингтона уже становится неверным применительно к принципу кратчайшего времени.

Рис.11 Движение груза по трём заданным траекториям в поле var1-.

Рис.12 Движение груза по трем заданным траекториям в поле var2-.

Если мы рассмотрим и движение груза в других полях (программа Hrono1 позволяет смоделировать 10 различных видов монополей), то мы лишний раз убедимся, что выводы сделанные из результатов движения в одном поле, могут полностью противоречить выводам сделанным для движения в другом поле. Например, движение по эллипсу осуществляется не только в поле var2- , но и в поле var1+, хотя сам характер движений при этом резко отличается (сравните траектории на рис. 13 и рис.14). Также возможно как бы комбинированное движение по гиперболо-эллипсу с образованием красивых розеточек как при движении в поле var2+ , так и в поле var1-, но характер этих движений опять-таки отличается (см. те же рисунки). Кстати, похожие розеточки получаются и в постоянном поле, а если закон изменения полей только немного отличается от строго линейной или квадратичной зависимости, то вариантов движения уже может быть бесконечное