

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Оснащения врачебно-сестринской бригады.
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Интересное:
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Разберем идею разностного метода решения .краевых задач на примере взаимодействия световых пучков (см. рис. 12.1), переобозначив в системе(12.1-1) интенсивность излучения вправо на Y, а интенсивность излучения влево на у (просто в целях удобства, чтобы не писать индекс).

рис 12.1
Суть метода заключается в покрытии расчетного интервала сеткой из N точек. Тем самым определяются (N-i) шагов (рис. 12.7). Затем надо заменить дифференциальные уравнения исходной краевой задачи аппроксимирующими их уравнениями в конечных разностях, выписав соответствующие разностные уравнения для каждого 1-го шага. В нашем случае достаточно просто заменить первые производные из (12.1-1) их разностными аналогами (такой метод называется еще методом Эйлера):

Рис. 12.7. Сетка, покрывающая расчетный интервал
Примечание
Существует множество способов аппроксимации дифференциальных уравнений разностными. От выбора конкретного варианта зависит не только простота, быстрота и удобство вычислений, но и сама возможность получения правильного ответа.
Получилась система (по числу шагов) 2-(м-1) разностных линейных алгебраических уравнений с 2-N неизвестными YI и yi. Для того чтобы она имела единственное решение, надо дополнить число уравнений до 2-м. Это можно сделать, записав в разностном виде оба граничных условия:
Y0=1O, yN=R-YN.
Сформированная полная система алгебраических уравнений называется разностной схемой, аппроксимирующей исходную краевую задачу. Обратите внимание, что правые части разностных уравнений системы на каждом шаге записаны для левой границы шага. Такие разностные схемы называют явными, т. к. все значения YI+I и yi+i находятся в левой части уравнений. Полученную явную разностную схему легко записать в матричной форме
|
|
A.Z=B,
где z - неизвестный вектор, получающийся объединением векторов Y и у. Решив систему (3), мы получим решение краевой задачи.
Примечание
На самом деле, все несколько сложнее, поскольку, вообще говоря, необходимо еще доказать, что, во-первых, разностная схема действительно аппроксимирует дифференциальные уравнения и, во-вторых, при м-*» разностное решение действительно сходится к дифференциальному.
22. Устойчивые и асимптотически устойчивые решения разностных уравнений
Рассмотрим дифференциальное уравнение
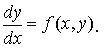
Пусть некоторое фиксированное решение y = φ(x) этого уравнения существует при всех x≥ x0 .
Решение y = φ(x) уравнения называется устойчивым по Ляпунову при x ≥ x0 , если для любого ε > 0 существует число δ > 0 (зависящее, вообще говоря, от ε ) такое, что:
— решение y = y(x) задачи Коши с начальным условием y(x0 ) , |y(x0) − φ(x0) | < δ , существует при всех x ≥ x0 ;
— для всех таких решений справедливо неравенство |y(x) − φ(x) | < ε , при всех x > x0 .
Геометрически это означает, что интегральные кривые y = y(x), близкие в момент x = x0 к интегральной кривой y = φ(x), остаются близкими к ней и на всем промежутке [x0, ∞) .
На рисунке красным изображено устойчивое решение задачи Коши y' = − y, y(1) = 1.
Видно, что все интегральные кривые, близкие к этому решению в начальный момент x = 1, остаются вблизи него и при x > 1 .

Решение y = φ(x) называется неустойчивым по Ляпунову при x ≥ x0 , если существует число ε > 0 такое, что для любого δ > 0
найдутся решения y = yδ(x) и значение x1 = x1(δ) > x0 такие, что хотя | yδ( x0) − φ( x0) | < δ , но |y( x1) − φ( x1) | ≥ ε .
На рисунке красным изображено неустойчивое решение y = 0 задачи Коши y' = sin2 y, y(0) = 0.

Видно, что интегральные кривые, близкие к y = 0 в начальный момент x0 = 0, удаляются от y = 0 с ростом x > 1 .
|
|
2f(n+2)-2f(n+1)+f(n)=0
2л^2-2л+1=0
D= - 4
л(1)=(2+2i)/4=(1+i)/2
л(2)=(2-2i)/4=(1-i)/2
y=(e)^0.5x*(C1*cos0.5x+C2*sin0.5x)
(0.5)^n*(C1*cos(n*pi)/4+C2*sin(n*pi)/4)
л=a+ib
л=sqr(a*a+b*b)>=1
1) Если л1 и л2 <1, то решение устойчиво
2) Если л1 и л2 >1, то решение неустойчиво
3) Если л1 и л2 =1, то решение устойчиво (но не ассимптотически)
4) Если хотя бы одно л>1, то неустойчиво
Размещено на Allbest.ru
|
|
|

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!