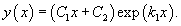Уравнение F(x, y, y ') = 0,
где y = y(x) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.
Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y '(x)) ≡ 0 для всех x из (a,b) .
График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.
Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.
Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x0) = y0, называется задачей Коши (или начальной задачей).
Условие y(x0) = y0 — начальное условие.
Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.
Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.
Пример ДУ 1-го порядка.
Найти общее и частное решение дифференциального уравнения 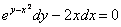 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . Выполнить проверку.
. Выполнить проверку.
Решение: Сначала найдем общее решение. Разделяем переменные:

Интегрируем уравнение:

Интеграл слева – табличный, интеграл справа – берем методом подведения функции под знак дифференциала:
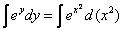
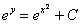
Выражаем общее решение:

Итак, общее решение:
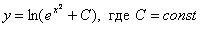
Найдем частное решение, соответствующее заданному начальному условию  . В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
. В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
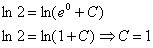
Более привычное оформление:
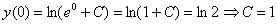
Подставляем найденное значение константы 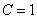 в общее решение.
в общее решение.
частное решение:

Теорема существования и единственности.
Рассмотрим обыкновенное дифференциальное уравнение 1–го порядка, записанное в нормальной форме:
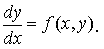
Областью определения уравнения называется область D определения правой части уравнения f(x, y), D ⊂ R2 .
Функция y = y(x) является решением задачи Коши
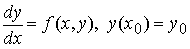
если y = y(x) дифференцируема на [a, b] , (x, y(x)) ∈ D для всех x из [a, b] , y(x0) = y0 , x0∈[a, b], и при подстановке в уравнение обращает его в тождество:
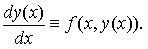
Фундаментальным результатом теории обыкновенных дифференциальных уравнений является теорема существования и единственности решения задачи Коши:
Пусть функция f(x, y) и ее частная производная fy(x, y) непрерывны в некоторой области D плоскости x0y и точка (x0, y0) принадлежит области D.
Тогда :
— в некоторой окрестности (x0 − δ, x0 + δ) точки x0 существует решение задачи Коши
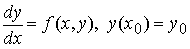
— если y = φ1(x) и y = φ2(x) два решения задачи Коши, то φ1(x) = φ2(x) на (x0 − δ, x0 + δ) .
Геометрически это означает, что если условия теоремы выполнены, то через каждую точку (x0, y0) области D проходит единственная интегральная кривая уравнения.
Бесконечное множество решений уравнения
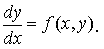
можно рассматривать как однопараметрическое семейство функций y = φ(x; x0) — семейство решений задачи Коши
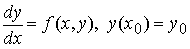
элементы которого различны для разных значений x0 . Иными словами область D "расслаивается" на интегральные кривые y = φ(x; x0) .
Важно понимать, что результат теоремы имеет локальный характер — существование и единственность решения гарантированы, вообще говоря, только в малой окрестности точки x0 . Важно также понимать, что условия теоремы существования и единственности достаточные условия. Нарушение условий теоремы не означает, что решение задачи не существует либо что оно не единственно.
3. Интегрирование некоторых типов ОДУ первого порядка:
a. с разделяющимися переменными
b. однородные
c. линейные
d. Бернулли
e. в полных дифференциалах
а) Уравнения с разделяющимися переменными
Так называются уравнения вида

 или(11)
или(11)
f1(x) g1(y) dx + f2(x) g2(y) dy = 0  (12)
(12)
Примеры: 1.
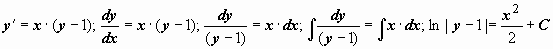 .
.
При такой форме записи общего интеграла решение y = 1 потеряно. Можно преобразовать общее решение к виду, который содержит это решение. Переобозначим постоянную C как ln|C1|:
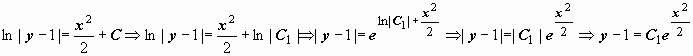
Вернёмся к обозначению постоянной интегрирования C; общее решение 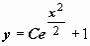 содержит частное решение y = 1 при C = 0.
содержит частное решение y = 1 при C = 0.
Пример:
 .
. 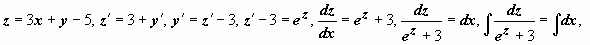


b) Однородные уравнения
 .(13)
.(13)
Это уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции u(x) заменой  , или
, или  . Подставляя в (13) y = u,
. Подставляя в (13) y = u, 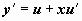 , получим
, получим  (это - уравнение с разделяющимися переменными),
(это - уравнение с разделяющимися переменными),  - это общий интеграл уравнения относительно переменных x, u.
- это общий интеграл уравнения относительно переменных x, u.
Пример:

 -
-
общее решение уравнения.  Примеры: 1. (y2 - 2xy)dx + x2dy = 0. Здесь коэффициенты при дифференциалах - однородные функции второй степени, т.е. уравнение должно приводиться к виду (13). Решаем уравнение относительно производной:
Примеры: 1. (y2 - 2xy)dx + x2dy = 0. Здесь коэффициенты при дифференциалах - однородные функции второй степени, т.е. уравнение должно приводиться к виду (13). Решаем уравнение относительно производной:  делим числитель и знаменатель правой части на x2:
делим числитель и знаменатель правой части на x2: 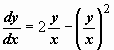 - это уравнении с однородной правой частью.
- это уравнении с однородной правой частью.
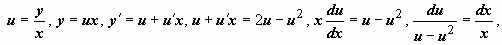
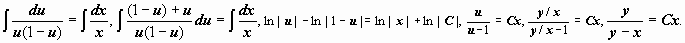
Это общий интеграл уравнения.
c) Линейные уравнения
ДУ первого порядка называется линейным, если неизвестная функция y(x) и её производная  входят в уравнение в первой степени:
входят в уравнение в первой степени:
 .(14)
.(14)
Здесь p(x), q(x) - непрерывные функции.
Для решения уравнения (14) представим y(x) в виде произведения двух новых неизвестных функций u(x) и v(x): y(x) = u(x) v(x). Тогда
 ,
,
и уравнение приводится к виду
 , или
, или 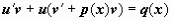 .
.
Пример:
 .
.
Решение:
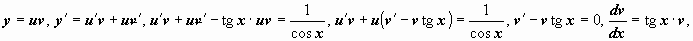
 .
.
Теперь для u(x) получим:  , и общее решение уравнения
, и общее решение уравнения  . Для нахождения частного решения, соответствующего начальным условиям задачи Коши, подставим в общее решение
. Для нахождения частного решения, соответствующего начальным условиям задачи Коши, подставим в общее решение 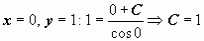 . Решение задачи:
. Решение задачи: 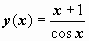 .
.
d) Бернулли
 .(15)
.(15)
где  (при m = 0 уравнение линейно, при m = 1 - с разделяющимися переменными).
(при m = 0 уравнение линейно, при m = 1 - с разделяющимися переменными).
Уравнение Бернулли сводится к линейному подстановкой z = y1-m (при m>1 может быть потеряно решение y = 0). Действительно, 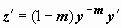 ,
, 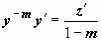 ; после деления уравнения (15) на ym получим
; после деления уравнения (15) на ym получим 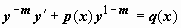 , или
, или 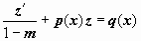 - линейное уравнение.
- линейное уравнение.
Пример: 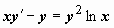 (уравнение Бернулли, m = 2). Подстановка
(уравнение Бернулли, m = 2). Подстановка  . Решаем полученное линейное уравнение:
. Решаем полученное линейное уравнение:
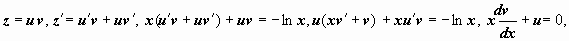
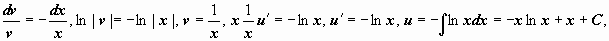
 .
.
e) В полных дифференциалах
P(x, y) dx + Q(x, y) dy = 0.(16)
(P(x, y), Q(x, y) - непрерывно дифференцируемы) в случае, если его левая часть является полным дифференциалом некоторой функции u(x, y), т.е. если существует такая функция u(x, y), что 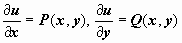 . Необходимым и достаточным условием существования такой функции является условие
. Необходимым и достаточным условием существования такой функции является условие  . Если (16) - уравнение в полных дифференциалах, то его правая часть равна
. Если (16) - уравнение в полных дифференциалах, то его правая часть равна 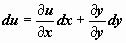 , т.е. (16) принимает вид du(x, y) = 0. На решении y(x) получим du(x, y(x)) = 0, следовательно, u(x, y(x)) = C, где C - произвольная постоянная. Соотношение u(x, y) = C и есть общее решение уравнения в полных дифференциалах.
, т.е. (16) принимает вид du(x, y) = 0. На решении y(x) получим du(x, y(x)) = 0, следовательно, u(x, y(x)) = C, где C - произвольная постоянная. Соотношение u(x, y) = C и есть общее решение уравнения в полных дифференциалах.
 Для нахождения функции u(x, y) решается система уравнений
Для нахождения функции u(x, y) решается система уравнений

Из первого уравнения этой системы находим  с точностью до произвольной дифференцируемой по y функции
с точностью до произвольной дифференцируемой по y функции  (эта функция играет роль постоянной интегрирования; так как интегрирование ведётся по переменной x); затем из второго уравнения определяется
(эта функция играет роль постоянной интегрирования; так как интегрирование ведётся по переменной x); затем из второго уравнения определяется  .
.
Пример: найти общее решение уравнения
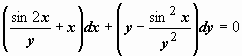 .
.
Убедимся, что это - уравнение в полных дифференциалах. Здесь
 ;
;
 ,
,
т.е. это действительно уравнение рассматриваемого типа. Ищем функцию u(x, y) такую, что  Из первого уравнения
Из первого уравнения
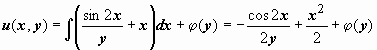 .
.
Дифференцируем эту функцию по y и приравниваем выражению, стоящему во втором уравнении системы:
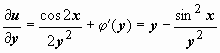 .
.
Если мы правильно решаем это уравнение (т.е. правильно определили его тип и правильно выполнили предыдущие действия), то в полученном уравнении для  должны остаться только члены, зависящие от y. Действительно, представляя
должны остаться только члены, зависящие от y. Действительно, представляя 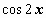 как
как  , получим
, получим

Следовательно,  , и общее решение уравнения имеет вид
, и общее решение уравнения имеет вид  .
.
4. ОДУ высших порядков, допускающих понижение порядка
Опр. Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).
Некоторые типы уравнений, допускающие понижение порядка.
1) Уравнение вида  решается последовательным n-кратным интегрированием. Пример:
решается последовательным n-кратным интегрированием. Пример:

Переобозначив постояные, общее решение запишем в виде y = cos x + C1x3 + C2x2 + C3x + C4.
2) Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные. Порядок уравнения вида F(x, y(k), y(k+1), y(k+2), …,y(n)) = 0, не содержащего функции y(x) и k - 1 младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z(x) = y(k)(x). Тогда  z(n-k) = y(n)(x), и относительно z(x) уравнение примет вид
z(n-k) = y(n)(x), и относительно z(x) уравнение примет вид 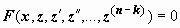 , т.е. будет уравнением n - k-го порядка. После нахождения z(x)последовательным интегрированием решается уравнение y(k) = z(x).
, т.е. будет уравнением n - k-го порядка. После нахождения z(x)последовательным интегрированием решается уравнение y(k) = z(x).
 Пример: решить задачу Коши:
Пример: решить задачу Коши:
 .
.
Младшая производная, входящая в явной форме в уравнения, - вторая, поэтому делаем замену искомой функции  . Тогда
. Тогда 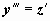 , и уравнение примет вид
, и уравнение примет вид  . Это - уравнение Бернулли; пусть
. Это - уравнение Бернулли; пусть
z = uv,
тогда
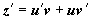 ,
,
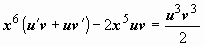
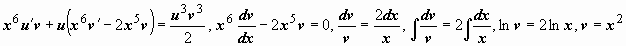
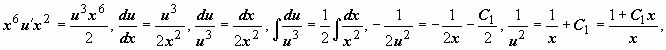
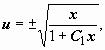
следовательно,
 .
.
Относительно y(x) - это уравнение
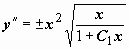 .
.
Мы можем последовательно находить
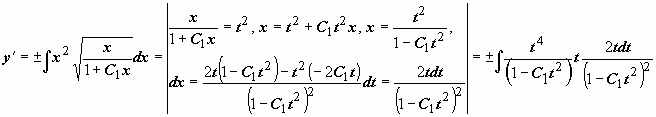
и так далее, однако в этом нет необходимости. Так как мы решаем задачу Коши, то из начального условия 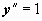 при x = 1 можно определить и знак частного решения, и значение постоянной C1:
при x = 1 можно определить и знак частного решения, и значение постоянной C1:  . Теперь
. Теперь 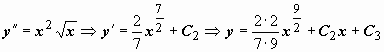 . Из условия
. Из условия 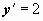 при x = 1 находим C2:
при x = 1 находим C2: 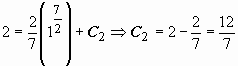 ; из условия y = 3 при x = 1 находим C3:
; из условия y = 3 при x = 1 находим C3:
 .
.
Окончательный ответ: 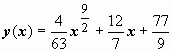 .
.
 3)Уравнение, не содержащее в явном виде независимую переменную x. Порядок уравнения
3)Уравнение, не содержащее в явном виде независимую переменную x. Порядок уравнения  , не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость
, не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость 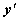 от y:
от y:  . Старшие производные y по x вычисляются по правилу дифференцирования сложной функции:
. Старшие производные y по x вычисляются по правилу дифференцирования сложной функции:
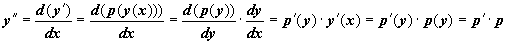 .
.
Аналогично,

Также находятся следующие производные, и всегда k -ая производная y по x выражается через k-1 -ую производную p по y. В случае уравнения второго порядка  в результате таких преобразований получим
в результате таких преобразований получим  , т.е. уравнение первого порядка (в котором y выступает как аргумент, p(y) - как неизвестная функция). После нахождения решения p = p(y, C1)этого уравнения решается уравнение
, т.е. уравнение первого порядка (в котором y выступает как аргумент, p(y) - как неизвестная функция). После нахождения решения p = p(y, C1)этого уравнения решается уравнение 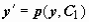 , решение которого y = y(x, C1, C2) будет общим решением исходного уравнения.
, решение которого y = y(x, C1, C2) будет общим решением исходного уравнения.
Пример.
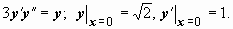
Решение:
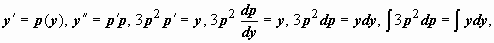
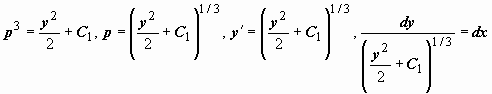 .
.
Интеграл от дифференциала в левой части этого равенства вообще не берётся, поэтому проверим, не упростится ли задача, если использовать начальные условия. Так как при x = 0 должно быть  , то получим
, то получим
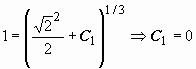 .
.
Поэтому частное решение должно удовлетворять уравнению
 .
.
Находим  :
:  . Ответ: решение задачи Коши
. Ответ: решение задачи Коши  .
.
4) Применение интегрируемых комбинаций. Иногда удаётся заметить, что в уравнении 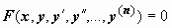 правая часть является производной некоторой функции
правая часть является производной некоторой функции  , т.е. уравнение имеет вид
, т.е. уравнение имеет вид 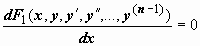 . Интегрируя по x, получим уравнение, порядок которого на единицу меньше порядка исходного уравнения (так называемый первый интеграл уравнения):
. Интегрируя по x, получим уравнение, порядок которого на единицу меньше порядка исходного уравнения (так называемый первый интеграл уравнения):  .
.
 Пример:
Пример:  . Если переписать это уравнение в виде
. Если переписать это уравнение в виде 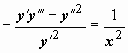 и сообразить, что справа стоит производная функции
и сообразить, что справа стоит производная функции 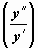 , то получим
, то получим  , откуда
, откуда 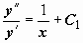 . Это уравнение не содержит явно y, поэтому
. Это уравнение не содержит явно y, поэтому

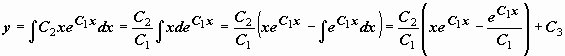 .
.
5. Линейные однородные ОДУ второго порядка
a. линейная зависимость и независимость функций
b. критерий линейной зависимости двух решений линейного однородного ОДУ второго порядка в терминах определителя Вронского
c. теорема о структуре общего решения
ЛДУ 2-го порядка называется ДУ 2-го порядка, линейное относительно у, у', у ", т.е.
 (21.3)
(21.3)
Дифференциальное уравнение
 (21.4)
(21.4)
получающееся из (21.3) при b(х) = О, называется линейным однородным ДУ 2-го порядка (ЛОДУ 2п). Если b(х)  О, то уравнение называется линейным неоднородным (ЛНДУ 2п).
О, то уравнение называется линейным неоднородным (ЛНДУ 2п).
Из теоремы Коши следует, что при непрерывности функций  в окрестности т.
в окрестности т.  при
при  уравнение (21.3) имеет в окрестности т.
уравнение (21.3) имеет в окрестности т. 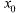 единственное решение.
единственное решение.
Определение. Система функций f1(x), f2(x), …, fn(x) называется линейно зависимой, если существуют система постоянных c1, c2, … , cn, такая, что  , и для которой будет выполнено соотношение
, и для которой будет выполнено соотношение  . В противном случае система функций будет называться линейно независимой.
. В противном случае система функций будет называться линейно независимой.
Определение. Определитель вида
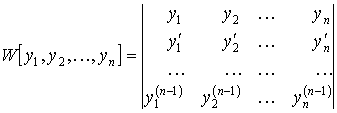
называется определителем Вронского.
Теорема. Если система функций линейно зависима, то определитель Вронского равен тождественно нулю.
Доказательство. Пусть система функций f1(x), f2(x), …, fn(x) линейно зависима, то есть не для всех одновременно равных нулю c1, c2, … , cn выполняется соотношение
c1 ·f1(x) + c2 ·f2(x) + … + cn·fn(x) ≡ 0. (4)
Дифференцируя соотношение (4) n - 1 раз, составим систему алгебраических уравнений относительно c1, c2, … , cn
 (5)
(5)
Так как однородная система линейных алгебраических уравнений имеет нетривиальное решение, то её главный определитель тождественно равен нулю. Поскольку для системы (5) главный определитель совпадает с определителем Вронского, то отсюда и вытекает справедливость теоремы.
Теорема структуре общего решения: Пусть  непрерывны на
непрерывны на  Если решения уравнения
Если решения уравнения 
(21.4) образуют фундаментальную систему решений,  то
то  является общим решением
является общим решением
уравнения (21.4) на 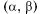 Проверим выполнение условий из определения общего решения. По теореме о линейной комбинации решений
Проверим выполнение условий из определения общего решения. По теореме о линейной комбинации решений 
 является решением уравнения (21.4). Возьмем начальные условия
является решением уравнения (21.4). Возьмем начальные условия  Подставляя их в
Подставляя их в 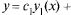
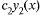 для определения
для определения 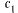 и
и 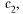 получаем систему
получаем систему
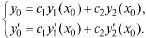 (21.5)
(21.5)
Ее определитель 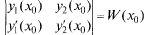 является определите-
является определите-
лем Вронского, вычисленным в т. 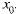 Он не равен нулю по условию теоремы, поэтому система имеет единственное решение
Он не равен нулю по условию теоремы, поэтому система имеет единственное решение 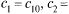
 которое может быть записано по формулам Крамера. Таким образом, выполнены оба условия определения общего решения
которое может быть записано по формулам Крамера. Таким образом, выполнены оба условия определения общего решения
6. Линейные однородные ОДУ второго порядка с постоянными коэффициентами
d. характеристическое уравнение, характеристические числа
e. общее решение при  и
и  (вещ.)
(вещ.)
f. общее решение при комплексно-сопряженных корнях характеристического уравнения, его вещественная форма
Рассмотрим линейное дифференциальное уравнение вида
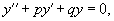
где p, q − постоянные коэффициенты.
А. характеристическое уравнение:
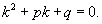
при помощи замены
 - через
- через  ,
,  - через
- через 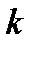 ,
, 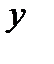 - через 1
- через 1
составляется характеристическое уравнение, соответствующее данному ЛОДУ; решается характеристическое уравнение, находятся корни:  устанавливается характер корней (действительные или комплексные, различные или кратные) и определяется соответствующая этим корням фундаментальная система решений
устанавливается характер корней (действительные или комплексные, различные или кратные) и определяется соответствующая этим корням фундаментальная система решений  ;составляется общее решение ЛОДУ:
;составляется общее решение ЛОДУ: 
Б. Обшее решение OДУ зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением.След. случаи:
1.Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения r1 и r2 действительны и различны. В этом случае общее решение описывается функцией
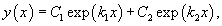 где C1 и C2 − произвольные действительные числа
где C1 и C2 − произвольные действительные числа
2 . Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид: 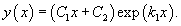
B. Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде



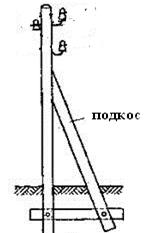
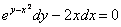 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . Выполнить проверку.
. Выполнить проверку.

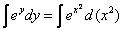
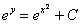

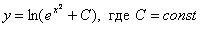
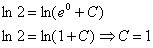
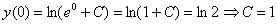
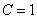 в общее решение.
в общее решение.
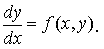
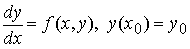
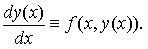

 или(11)
или(11)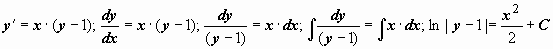 .
.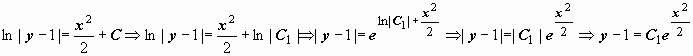
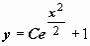 содержит частное решение y = 1 при C = 0.
содержит частное решение y = 1 при C = 0. .
. 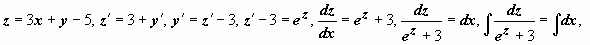


 .(13)
.(13) , или
, или  . Подставляя в (13) y = u,
. Подставляя в (13) y = u, 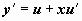 , получим
, получим  (это - уравнение с разделяющимися переменными),
(это - уравнение с разделяющимися переменными),  - это общий интеграл уравнения относительно переменных x, u.
- это общий интеграл уравнения относительно переменных x, u.
 -
- делим числитель и знаменатель правой части на x2:
делим числитель и знаменатель правой части на x2: 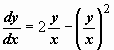 - это уравнении с однородной правой частью.
- это уравнении с однородной правой частью.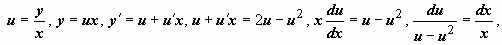
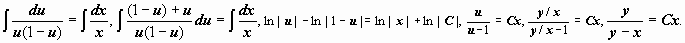
 входят в уравнение в первой степени:
входят в уравнение в первой степени: .(14)
.(14) ,
, , или
, или 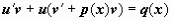 .
. .
.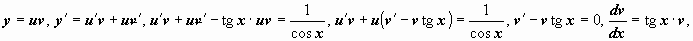
 .
. , и общее решение уравнения
, и общее решение уравнения  . Для нахождения частного решения, соответствующего начальным условиям задачи Коши, подставим в общее решение
. Для нахождения частного решения, соответствующего начальным условиям задачи Коши, подставим в общее решение 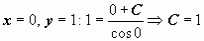 . Решение задачи:
. Решение задачи: 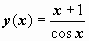 .
. .(15)
.(15) (при m = 0 уравнение линейно, при m = 1 - с разделяющимися переменными).
(при m = 0 уравнение линейно, при m = 1 - с разделяющимися переменными).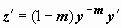 ,
, 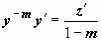 ; после деления уравнения (15) на ym получим
; после деления уравнения (15) на ym получим 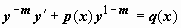 , или
, или 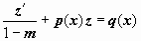 - линейное уравнение.
- линейное уравнение.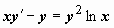 (уравнение Бернулли, m = 2). Подстановка
(уравнение Бернулли, m = 2). Подстановка  . Решаем полученное линейное уравнение:
. Решаем полученное линейное уравнение: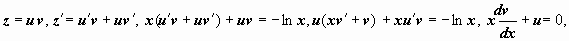
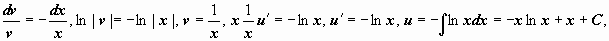
 .
.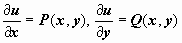 . Необходимым и достаточным условием существования такой функции является условие
. Необходимым и достаточным условием существования такой функции является условие  . Если (16) - уравнение в полных дифференциалах, то его правая часть равна
. Если (16) - уравнение в полных дифференциалах, то его правая часть равна 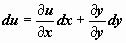 , т.е. (16) принимает вид du(x, y) = 0. На решении y(x) получим du(x, y(x)) = 0, следовательно, u(x, y(x)) = C, где C - произвольная постоянная. Соотношение u(x, y) = C и есть общее решение уравнения в полных дифференциалах.
, т.е. (16) принимает вид du(x, y) = 0. На решении y(x) получим du(x, y(x)) = 0, следовательно, u(x, y(x)) = C, где C - произвольная постоянная. Соотношение u(x, y) = C и есть общее решение уравнения в полных дифференциалах.
 с точностью до произвольной дифференцируемой по y функции
с точностью до произвольной дифференцируемой по y функции  (эта функция играет роль постоянной интегрирования; так как интегрирование ведётся по переменной x); затем из второго уравнения определяется
(эта функция играет роль постоянной интегрирования; так как интегрирование ведётся по переменной x); затем из второго уравнения определяется 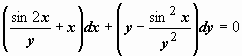 .
. ;
; ,
, Из первого уравнения
Из первого уравнения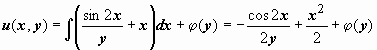 .
.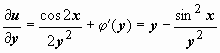 .
. должны остаться только члены, зависящие от y. Действительно, представляя
должны остаться только члены, зависящие от y. Действительно, представляя 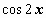 как
как  , получим
, получим
 , и общее решение уравнения имеет вид
, и общее решение уравнения имеет вид  .
. решается последовательным n-кратным интегрированием. Пример:
решается последовательным n-кратным интегрированием. Пример:
 z(n-k) = y(n)(x), и относительно z(x) уравнение примет вид
z(n-k) = y(n)(x), и относительно z(x) уравнение примет вид 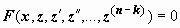 , т.е. будет уравнением n - k-го порядка. После нахождения z(x)последовательным интегрированием решается уравнение y(k) = z(x).
, т.е. будет уравнением n - k-го порядка. После нахождения z(x)последовательным интегрированием решается уравнение y(k) = z(x). .
. . Тогда
. Тогда 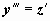 , и уравнение примет вид
, и уравнение примет вид  . Это - уравнение Бернулли; пусть
. Это - уравнение Бернулли; пусть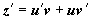 ,
,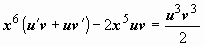
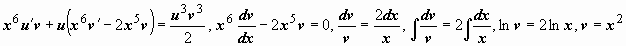
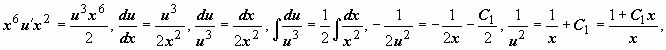
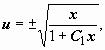
 .
.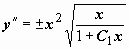 .
.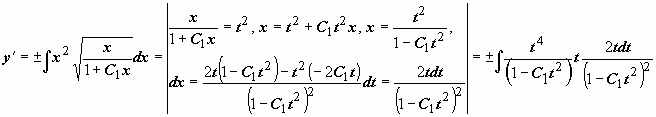
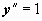 при x = 1 можно определить и знак частного решения, и значение постоянной C1:
при x = 1 можно определить и знак частного решения, и значение постоянной C1:  . Теперь
. Теперь 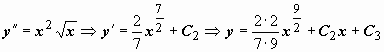 . Из условия
. Из условия 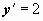 при x = 1 находим C2:
при x = 1 находим C2: 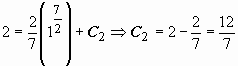 ; из условия y = 3 при x = 1 находим C3:
; из условия y = 3 при x = 1 находим C3: .
.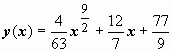 .
. , не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость
, не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость 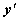 от y:
от y:  . Старшие производные y по x вычисляются по правилу дифференцирования сложной функции:
. Старшие производные y по x вычисляются по правилу дифференцирования сложной функции: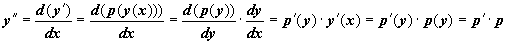 .
.
 в результате таких преобразований получим
в результате таких преобразований получим  , т.е. уравнение первого порядка (в котором y выступает как аргумент, p(y) - как неизвестная функция). После нахождения решения p = p(y, C1)этого уравнения решается уравнение
, т.е. уравнение первого порядка (в котором y выступает как аргумент, p(y) - как неизвестная функция). После нахождения решения p = p(y, C1)этого уравнения решается уравнение 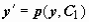 , решение которого y = y(x, C1, C2) будет общим решением исходного уравнения.
, решение которого y = y(x, C1, C2) будет общим решением исходного уравнения.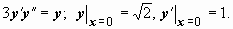
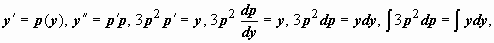
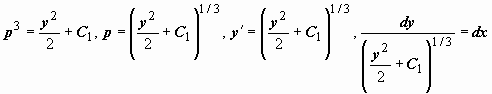 .
. , то получим
, то получим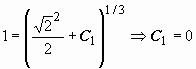 .
. .
. :
:  . Ответ: решение задачи Коши
. Ответ: решение задачи Коши  .
.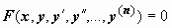 правая часть является производной некоторой функции
правая часть является производной некоторой функции  , т.е. уравнение имеет вид
, т.е. уравнение имеет вид 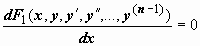 . Интегрируя по x, получим уравнение, порядок которого на единицу меньше порядка исходного уравнения (так называемый первый интеграл уравнения):
. Интегрируя по x, получим уравнение, порядок которого на единицу меньше порядка исходного уравнения (так называемый первый интеграл уравнения):  .
.  . Если переписать это уравнение в виде
. Если переписать это уравнение в виде 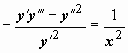 и сообразить, что справа стоит производная функции
и сообразить, что справа стоит производная функции 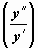 , то получим
, то получим  , откуда
, откуда 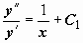 . Это уравнение не содержит явно y, поэтому
. Это уравнение не содержит явно y, поэтому
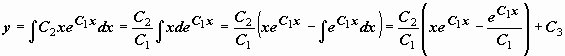 .
. (21.3)
(21.3) (21.4)
(21.4) О, то уравнение называется линейным неоднородным (ЛНДУ 2п).
О, то уравнение называется линейным неоднородным (ЛНДУ 2п). в окрестности т.
в окрестности т.  при
при  уравнение (21.3) имеет в окрестности т.
уравнение (21.3) имеет в окрестности т.  единственное решение.
единственное решение. , и для которой будет выполнено соотношение
, и для которой будет выполнено соотношение  . В противном случае система функций будет называться линейно независимой.
. В противном случае система функций будет называться линейно независимой.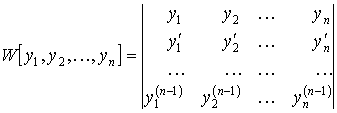
 (5)
(5)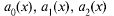 непрерывны на
непрерывны на  Если решения уравнения
Если решения уравнения 
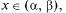 то
то  является общим решением
является общим решением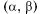 Проверим выполнение условий из определения общего решения. По теореме о линейной комбинации решений
Проверим выполнение условий из определения общего решения. По теореме о линейной комбинации решений 
 является решением уравнения (21.4). Возьмем начальные условия
является решением уравнения (21.4). Возьмем начальные условия  Подставляя их в
Подставляя их в 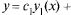
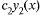 для определения
для определения 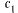 и
и 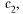 получаем систему
получаем систему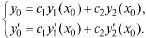 (21.5)
(21.5)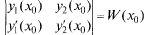 является определите-
является определите-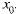 Он не равен нулю по условию теоремы, поэтому система имеет единственное решение
Он не равен нулю по условию теоремы, поэтому система имеет единственное решение 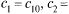
 которое может быть записано по формулам Крамера. Таким образом, выполнены оба условия определения общего решения
которое может быть записано по формулам Крамера. Таким образом, выполнены оба условия определения общего решения и
и  (вещ.)
(вещ.)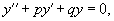
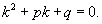
 - через
- через  ,
,  - через
- через 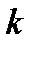 ,
, 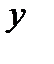 - через 1
- через 1 устанавливается характер корней (действительные или комплексные, различные или кратные) и определяется соответствующая этим корням фундаментальная система решений
устанавливается характер корней (действительные или комплексные, различные или кратные) и определяется соответствующая этим корням фундаментальная система решений  ;составляется общее решение ЛОДУ:
;составляется общее решение ЛОДУ: 
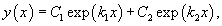 где C1 и C2 − произвольные действительные числа
где C1 и C2 − произвольные действительные числа