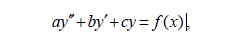
Дифференциальные уравнения вида
где a,b,c – числа, называют линейными неоднородными дифференциальными уравнениями 2-го порядка с постоянными коэффициентами.
Общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами имеет вид:
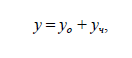
где yо – общее решение однородного уравнения, а yч – какое-нибудь решение неоднородного уравнения (частное решение).
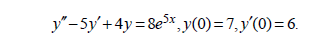
Пример 7. Решить задачу Коши
Решение. Найдем сначала общее решение однородного уравнения
Для этого составим характеристическое уравнение:
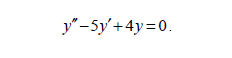


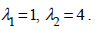
Это уравнение имеет два различных вещественных корня:
Следовательно, общим решением однородного уравнения является функция
Найдем теперь какое-нибудь частное решение неоднородного уравнения
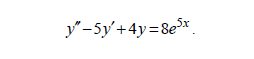
Будем искать его в виде
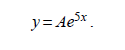
Тогда

Подставив эти выражения в уравнение, получим:


Теперь можно выписать общее решение неоднородного уравнения:
Вычислим производную:
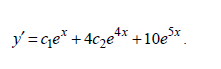
Воспользовавшись начальными условиями, получим систему уравнений:
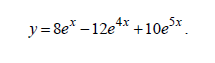
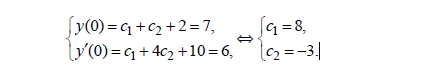
Искомое решение задачи Коши имеет вид:
(Как мне кажется, в последней строчке здесь ошибка, т.к. наши найденные C1 и C2 здесь подставили в y’, а не в y)
10. Отыскание частного решения линейных неоднородных ОДУ для правой части специального вида методом неопределенных коэффициентов
Рассмотрим решение линейных неоднородных уравнений второго порядка с постоянными коэффициентами, т.е. уравнений вида
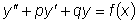 ,
,
где p и q - действительные числа.
Нам уже известно, что общее решение линейного неоднородного уравнения представляется как сумма какого-нибудь частного решения этого уравнения и общего решения Y соответствующего однородного уравнения. Частное решение неоднородного уравнения ищем в форме квадратного трехчлена. В случае уравнения с постоянными коэффициентами общее решение линейного однородного уравнения, как мы уже знаем, находится легко. Остановимся теперь на проблеме отыскания частного решения y* линейного неоднородного уравнения.
а)  .
.
Если  , то частное решение неоднородного уравнения ищем также в форме квадратного трехчлена:
, то частное решение неоднородного уравнения ищем также в форме квадратного трехчлена:
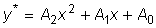 ,
,
где
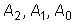 - неопределенные коэффициенты.
- неопределенные коэффициенты.
Отсюда
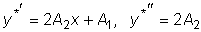 .
.
Подставляя эти выражения в исходное уравнение, мы получим тождество
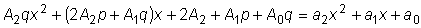 ,
,
Откуда
 .
.
Так как  , то из последней системы для коэффициентов
, то из последней системы для коэффициентов 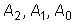 получаются определенные числовые значения. Тем самым частное решение y* будет вполне определено.
получаются определенные числовые значения. Тем самым частное решение y* будет вполне определено.
Если 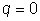 , то частное решение y* ищем в виде
, то частное решение y* ищем в виде 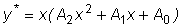 , когда один из корней характеристического уравнения равен нулю, и в виде
, когда один из корней характеристического уравнения равен нулю, и в виде
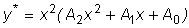 ,
,
когда оба корня характеристического уравнения нули. Аналогично обстоит дело, если f(x) - многочлен P(x) произвольной степени.
б) 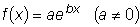 .
.
Частное решение ищем в виде
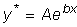 ,
,
где A - неопределенный коэффициент.
Отсюда
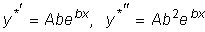 .
.
Подставляя эти выражения в исходное уравнение, после сокращения на e bx будем иметь
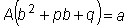 .
.
Отсюда видно, что если b не является корнем характеристического уравнения, то
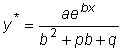 .
.
Если b - корень характеристического уравнения, то частное решение ищем в виде y* = Axebx , когда b - однократный корень, и в виде y* = P(x) ebx , когда b - двукратный корень.
Аналогично будет, если f(x) = P(x) ebx , где P(x) - многочлен.
в)  . (a и b не нули одновременно).
. (a и b не нули одновременно).
В этом случае частное решение y* ищем также в форме тригонометрического двучлена
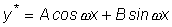 ,
,
где A и B - неопределенные коэффициенты.
Отсюда
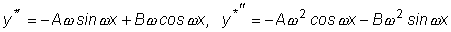 .
.
Подставляя эти выражения в исходное уравнение, получим:
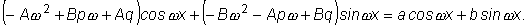 .
.
Так как последнее равенство представляет собой тождество, то коэффициенты при 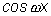 и
и  в левой и правой частях этого равенства должны быть соответственно равны друг другу. Поэтому
в левой и правой частях этого равенства должны быть соответственно равны друг другу. Поэтому
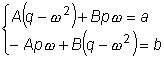 .
.
Эти уравнения определяют коэффициенты A и B , кроме случая, когда
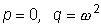
(или когда 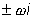 - корни характеристического уравнения).
- корни характеристического уравнения).
В последнем случае частное решение исходного уравнения ищем в виде
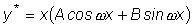 .
.



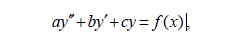
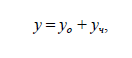
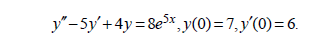
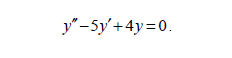


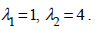
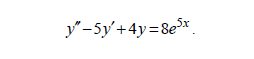
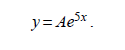



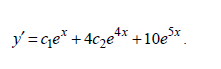
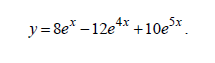
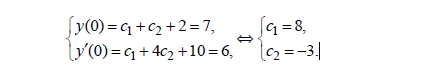
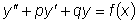 ,
, .
. , то частное решение неоднородного уравнения ищем также в форме квадратного трехчлена:
, то частное решение неоднородного уравнения ищем также в форме квадратного трехчлена: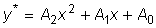 ,
,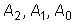 - неопределенные коэффициенты.
- неопределенные коэффициенты.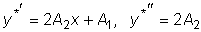 .
.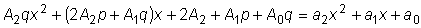 ,
, .
.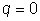 , то частное решение y* ищем в виде
, то частное решение y* ищем в виде 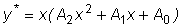 , когда один из корней характеристического уравнения равен нулю, и в виде
, когда один из корней характеристического уравнения равен нулю, и в виде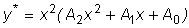 ,
,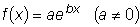 .
.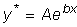 ,
,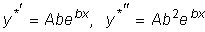 .
.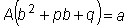 .
.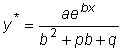 .
. . (a и b не нули одновременно).
. (a и b не нули одновременно).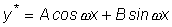 ,
,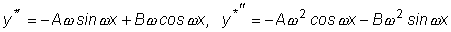 .
.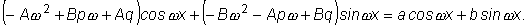 .
.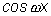 и
и  в левой и правой частях этого равенства должны быть соответственно равны друг другу. Поэтому
в левой и правой частях этого равенства должны быть соответственно равны друг другу. Поэтому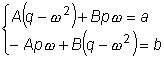 .
.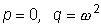
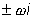 - корни характеристического уравнения).
- корни характеристического уравнения).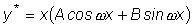 .
.


