Предположим, что для исследуемых социально-экономических переменных 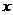 и
и 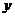 имеется
имеется 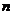 выборочных наблюдений
выборочных наблюдений 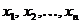 ,
, 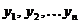 . На рисунке в системе прямоугольных координат нанесено поле рассеяния, точки которого соответствуют парам чисел (
. На рисунке в системе прямоугольных координат нанесено поле рассеяния, точки которого соответствуют парам чисел (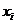 ,
,  ),
),
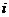 =1,…,
=1,…, 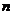 . На основе анализа поля рассеяния выдвигаем гипотезу о том, что зависимость
. На основе анализа поля рассеяния выдвигаем гипотезу о том, что зависимость 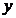 от
от 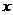 описывается линейной моделью вида:
описывается линейной моделью вида: 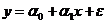 , где
, где 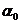 и
и 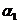 - неизвестные постоянные коэффициенты, а ε – случайная переменная (случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерений. Для модели
- неизвестные постоянные коэффициенты, а ε – случайная переменная (случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерений. Для модели  задача состоит в получении уравнения регрессии
задача состоит в получении уравнения регрессии 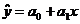 (прямая на рисунке), в котором коэффициенты
(прямая на рисунке), в котором коэффициенты 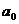 и
и 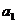 есть оценки неизвестных параметров
есть оценки неизвестных параметров 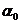 и
и 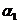 . Нахождение оценок
. Нахождение оценок 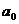 и
и 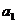 основывается на применении метода наименьших квадратов (МНК), суть которого состоит в следующем.
основывается на применении метода наименьших квадратов (МНК), суть которого состоит в следующем.
Рассмотрим точки A, B, C, изображенные на рисунке. Тогда |OC|= 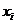 , |AC|=
, |AC|=  , |BC|=
, |BC|= 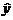 i=
i= 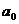 +
+ 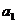
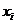 . Отклонение точки A от искомой прямой
. Отклонение точки A от искомой прямой  , измеренное по вертикали, будет равно
, измеренное по вертикали, будет равно 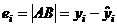 . Это отклонение может быть как положительным, так и отрицательным. Если все отклонения возвести в квадрат и сложить, то полученная величина будет непосредственно зависеть от разброса точек наблюдения от искомой линии.
. Это отклонение может быть как положительным, так и отрицательным. Если все отклонения возвести в квадрат и сложить, то полученная величина будет непосредственно зависеть от разброса точек наблюдения от искомой линии.
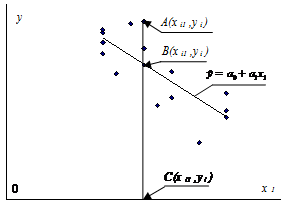
Различные значения 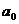 и
и 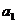 определяют различные линии, и им будут соответствовать различные суммы квадратов. Таким образом, сумма квадратов отклонений
определяют различные линии, и им будут соответствовать различные суммы квадратов. Таким образом, сумма квадратов отклонений 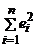 есть некоторая функция от
есть некоторая функция от 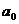 и
и 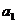 , т.е.
, т.е. 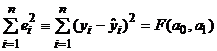 .
.
Далее пределы суммирования предполагаются такими же, и для упрощения записи будут опущены. Метод наименьших квадратов заключается в выборе таких значений 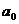 и
и 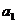 , для которых сумма квадратов отклонений
, для которых сумма квадратов отклонений 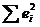 становится минимальной. Эта сумма является функцией оценок параметров
становится минимальной. Эта сумма является функцией оценок параметров 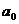 ,
, 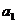 :
:  .
.
Поэтому нахождение оценок 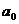 ,
, 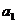 неизвестных параметров
неизвестных параметров 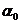 и
и 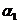 сводится к экстремальной задаче функции двух переменных F(
сводится к экстремальной задаче функции двух переменных F(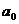 ,
, 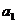 ):
):
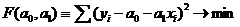 .
.
Необходимые условия минимума функции F(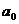 ,
, 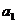 ) – равенство нулю частных производных:
) – равенство нулю частных производных:
 ,
,
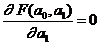 .
.
Вычислим эти частные производные:
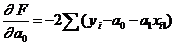 .
.
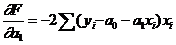 .
.
Приравняем их нулю и после элементарных преобразований получим систему двух линейных уравнений с двумя неизвестными 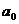 и
и 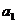 :
:
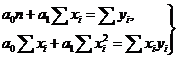
Эту систему уравнений называют системой нормальных уравнений. Ее решение может быть получено, например, по правилу Крамера:
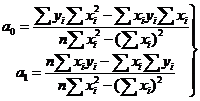
Для оценки качества полученного уравнения регрессии существует ряд характеристик, одной из которых является коэффициент парной корреляции.
Коэффициент парной корреляции 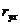 характеризует тесноту линейной зависимости между x и y. Он находится по формуле:
характеризует тесноту линейной зависимости между x и y. Он находится по формуле:  .
.
Для коэффициента парной корреляции выполняется соотношение:
- 1£ 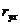 £ 1. Чем ближе значение |
£ 1. Чем ближе значение | 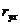 | к единице, тем теснее линейная связь между x и y. Если
| к единице, тем теснее линейная связь между x и y. Если
| 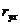 | =1, то между x и y существует функциональная зависимость вида
| =1, то между x и y существует функциональная зависимость вида 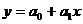 . Если величина |
. Если величина | 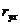 | близка к нулю, то это свидетельствует об отсутствии линейной зависимости между x и y, что не исключает возможность наличия нелинейной взаимосвязи между x и y. Близость значения коэффициента корреляции к нулю или единице носит относительный характер. Действительно, если
| близка к нулю, то это свидетельствует об отсутствии линейной зависимости между x и y, что не исключает возможность наличия нелинейной взаимосвязи между x и y. Близость значения коэффициента корреляции к нулю или единице носит относительный характер. Действительно, если 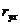 =0,99, то можно с уверенностью говорить о близости значения к единице и достаточно сильной линейной взаимосвязи между x и y. Но если
=0,99, то можно с уверенностью говорить о близости значения к единице и достаточно сильной линейной взаимосвязи между x и y. Но если 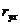 равен, например, 0,7, то говорить о его близости к единице оснований значительно меньше, а если
равен, например, 0,7, то говорить о его близости к единице оснований значительно меньше, а если 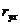 =0,5, то можно с равными основаниями говорить как о близости к нулю, так и о близости к единице.
=0,5, то можно с равными основаниями говорить как о близости к нулю, так и о близости к единице.
Для того чтобы с большей уверенностью полагаться на значение коэффициента корреляции, т.е. с большей уверенностью делать вывод о наличии или отсутствии линейной взаимосвязи между переменными y и x, разработан критерий проверки того, существенно ли отличие коэффициента корреляции от нуля или, как говорят, значимо ли значение коэффициента корреляции. Если в результате проверки выясняется, что коэффициент корреляции существенно отличается от нуля, то, несмотря даже на не очень близкое значение коэффициента к единице, делается вывод о наличии линейной взаимосвязи между переменными y и x. Если же подтверждается несущественное отличие 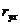 от нуля, то, несмотря на возможно достаточно большое значение коэффициента, делается вывод об отсутствии линейной взаимосвязи между переменными.
от нуля, то, несмотря на возможно достаточно большое значение коэффициента, делается вывод об отсутствии линейной взаимосвязи между переменными.
Проверка существенности отличия коэффициента парной корреляции от нуля (его значимости) проводится по схеме проверки статистических гипотез. Выдвигается нулевая гипотеза − коэффициент парной корреляции не является статистически значимым (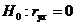 ). Вместе с ней выдвигается альтернативная гипотеза − существует положительная корреляционная зависимость (
). Вместе с ней выдвигается альтернативная гипотеза − существует положительная корреляционная зависимость (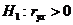 ). Для проверки гипотезы в качестве статистического критерия используется статистика t −Стьюдента с
). Для проверки гипотезы в качестве статистического критерия используется статистика t −Стьюдента с  степенями свободы:
степенями свободы:  Если
Если  , то гипотеза о существенном отличии коэффициента парной корреляции от нуля принимается, в противном случае − отвергается. В формуле
, то гипотеза о существенном отличии коэффициента парной корреляции от нуля принимается, в противном случае − отвергается. В формуле 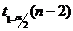 - квантиль порядка (1-a/2) распределения Стьюдента с (
- квантиль порядка (1-a/2) распределения Стьюдента с (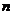 -2) степенями свободы (см. таблицу 2).
-2) степенями свободы (см. таблицу 2).
Коэффициентпарной корреляции  связан с коэффициентом
связан с коэффициентом 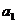 уравнения регрессии
уравнения регрессии 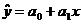 следующим образом:
следующим образом:  , где
, где  ,
,  − выборочные среднеквадратические отклонения случайных переменных x и y соответственно, рассчитывающиеся по формулам:
− выборочные среднеквадратические отклонения случайных переменных x и y соответственно, рассчитывающиеся по формулам:
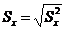 ,
,  ,
,
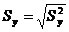 ,
,  .
.
Следующей важной характеристикой качества подбора уравнения регрессии является коэффициент детерминации, обозначаемый  . Определение
. Определение  и его содержательный смысл основан на следующей формуле:
и его содержательный смысл основан на следующей формуле:  ,
,
где 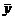 - выборочное среднее,
- выборочное среднее,  − выборочные значения зависимой переменной y,
− выборочные значения зависимой переменной y, 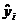 - значения зависимой переменной, вычисленные по уравнению регрессии
- значения зависимой переменной, вычисленные по уравнению регрессии 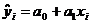 . Приведенная формула имеет глубокий содержательный смысл. Действительно, левая ее часть, т.е.
. Приведенная формула имеет глубокий содержательный смысл. Действительно, левая ее часть, т.е. 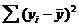 интерпретируется как мера общего разброса или рассеивания переменной y относительно ее среднего значения
интерпретируется как мера общего разброса или рассеивания переменной y относительно ее среднего значения  . Эта мера раскладывается на две составляющие. Первая часть
. Эта мера раскладывается на две составляющие. Первая часть  − это мера разброса, «объясненная» с помощью уравнения регрессии. Вторая часть
− это мера разброса, «объясненная» с помощью уравнения регрессии. Вторая часть 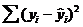 − это мера разброса, «не объясненного» уравнением регрессии. Слова «объясненный» и «не объясненный» взяты в кавычки, так как объяснение, в сущности, может оказаться мнимым. В действительности y может зависеть от какой-то другой переменной z, и x может действовать как величина, заменяющая z.
− это мера разброса, «не объясненного» уравнением регрессии. Слова «объясненный» и «не объясненный» взяты в кавычки, так как объяснение, в сущности, может оказаться мнимым. В действительности y может зависеть от какой-то другой переменной z, и x может действовать как величина, заменяющая z.
Коэффициент детерминации  определяется по формуле:
определяется по формуле:
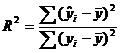 , или
, или 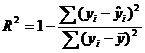 .
.
Очевидно, что 0 £  £ 1. Значение
£ 1. Значение  характеризует ту долю дисперсии переменной y, которая обуславливается, или которую можно «объяснить» уравнением регрессии
характеризует ту долю дисперсии переменной y, которая обуславливается, или которую можно «объяснить» уравнением регрессии 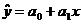 . Таким образом, чем ближе значение
. Таким образом, чем ближе значение  к единице, тем точнее уравнение регрессии отражает имеющуюся зависимость между переменными y и x. Максимальное значение коэффициента детерминации, равное единице, достигается, когда линия регрессии точно соответствует всем наблюдениям, так что
к единице, тем точнее уравнение регрессии отражает имеющуюся зависимость между переменными y и x. Максимальное значение коэффициента детерминации, равное единице, достигается, когда линия регрессии точно соответствует всем наблюдениям, так что 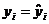 для всех наблюдений, и все остатки равны нулю. Если же в выборке отсутствует видимая связь между y и x, то
для всех наблюдений, и все остатки равны нулю. Если же в выборке отсутствует видимая связь между y и x, то  будет близок к нулю. Коэффициенты корреляции и детерминации для уравнения парной регрессии связаны между собой простым соотношением:
будет близок к нулю. Коэффициенты корреляции и детерминации для уравнения парной регрессии связаны между собой простым соотношением: 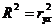 .
.
Качество уравнения регрессии оценивает F -тест. Он основан на проверке гипотезы  о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fнаб и критического (табличного) Fтаб значений F-статистики Фишера. Если Fтаб < Fнаб то гипотеза
о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fнаб и критического (табличного) Fтаб значений F-статистики Фишера. Если Fтаб < Fнаб то гипотеза  отклоняется и признается статистическая значимость уравнения регрессии. Если Fтаб > Fнаб то гипотеза
отклоняется и признается статистическая значимость уравнения регрессии. Если Fтаб > Fнаб то гипотеза  не отклоняется, и признается статистическая незначимость, ненадежность уравнения регрессии. Fнаб определяется как отношение объясненной суммы квадратов в расчете на одну независимую переменную к остаточной сумме квадратов в расчете на одну степень свободы:
не отклоняется, и признается статистическая незначимость, ненадежность уравнения регрессии. Fнаб определяется как отношение объясненной суммы квадратов в расчете на одну независимую переменную к остаточной сумме квадратов в расчете на одну степень свободы:
 .
.
Для парной регрессии 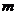 =1, поэтому
=1, поэтому
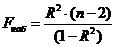 .
.
F-распределение Фишера зависит от степеней свободы df1 и df2 и от уровня значимости α. Количество степеней свободы df1 равно числу 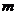 объясняющих переменных модели. Количество степеней свободы df2 определяется объемом выборки
объясняющих переменных модели. Количество степеней свободы df2 определяется объемом выборки 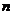 за вычетом числа объясняющих переменных модели df1 минус единица: df2 =
за вычетом числа объясняющих переменных модели df1 минус единица: df2 = 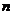 - df1 - 1. Значение Fтаб можно вычислить как по статистической таблице (см. таблицу 3), так и с помощью статистической функции из приложения MS Excel.
- df1 - 1. Значение Fтаб можно вычислить как по статистической таблице (см. таблицу 3), так и с помощью статистической функции из приложения MS Excel.



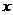 и
и 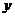 имеется
имеется 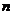 выборочных наблюдений
выборочных наблюдений 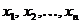 ,
, 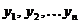 . На рисунке в системе прямоугольных координат нанесено поле рассеяния, точки которого соответствуют парам чисел (
. На рисунке в системе прямоугольных координат нанесено поле рассеяния, точки которого соответствуют парам чисел (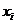 ,
,  ),
), 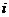 =1,…,
=1,…, 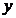 от
от 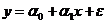 , где
, где 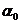 и
и 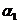 - неизвестные постоянные коэффициенты, а ε – случайная переменная (случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерений. Для модели
- неизвестные постоянные коэффициенты, а ε – случайная переменная (случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерений. Для модели  задача состоит в получении уравнения регрессии
задача состоит в получении уравнения регрессии 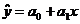 (прямая на рисунке), в котором коэффициенты
(прямая на рисунке), в котором коэффициенты 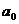 и
и 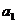 есть оценки неизвестных параметров
есть оценки неизвестных параметров 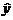 i=
i=  , измеренное по вертикали, будет равно
, измеренное по вертикали, будет равно 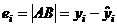 . Это отклонение может быть как положительным, так и отрицательным. Если все отклонения возвести в квадрат и сложить, то полученная величина будет непосредственно зависеть от разброса точек наблюдения от искомой линии.
. Это отклонение может быть как положительным, так и отрицательным. Если все отклонения возвести в квадрат и сложить, то полученная величина будет непосредственно зависеть от разброса точек наблюдения от искомой линии.
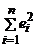 есть некоторая функция от
есть некоторая функция от 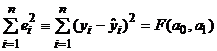 .
.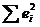 становится минимальной. Эта сумма является функцией оценок параметров
становится минимальной. Эта сумма является функцией оценок параметров  .
.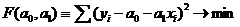 .
. ,
,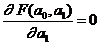 .
.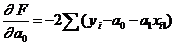 .
. 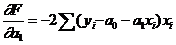 .
.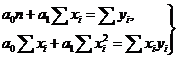
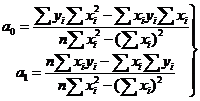
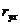 характеризует тесноту линейной зависимости между x и y. Он находится по формуле:
характеризует тесноту линейной зависимости между x и y. Он находится по формуле:  .
.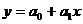 . Если величина |
. Если величина | 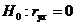 ). Вместе с ней выдвигается альтернативная гипотеза − существует положительная корреляционная зависимость (
). Вместе с ней выдвигается альтернативная гипотеза − существует положительная корреляционная зависимость (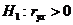 ). Для проверки гипотезы в качестве статистического критерия используется статистика t −Стьюдента с
). Для проверки гипотезы в качестве статистического критерия используется статистика t −Стьюдента с  степенями свободы:
степенями свободы:  Если
Если  , то гипотеза о существенном отличии коэффициента парной корреляции от нуля принимается, в противном случае − отвергается. В формуле
, то гипотеза о существенном отличии коэффициента парной корреляции от нуля принимается, в противном случае − отвергается. В формуле 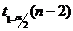 - квантиль порядка (1-a/2) распределения Стьюдента с (
- квантиль порядка (1-a/2) распределения Стьюдента с ( связан с коэффициентом
связан с коэффициентом 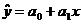 следующим образом:
следующим образом:  , где
, где  ,
,  − выборочные среднеквадратические отклонения случайных переменных x и y соответственно, рассчитывающиеся по формулам:
− выборочные среднеквадратические отклонения случайных переменных x и y соответственно, рассчитывающиеся по формулам: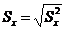 ,
,  ,
,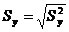 ,
,  .
. . Определение
. Определение  ,
,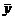 - выборочное среднее,
- выборочное среднее, 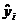 - значения зависимой переменной, вычисленные по уравнению регрессии
- значения зависимой переменной, вычисленные по уравнению регрессии 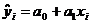 . Приведенная формула имеет глубокий содержательный смысл. Действительно, левая ее часть, т.е.
. Приведенная формула имеет глубокий содержательный смысл. Действительно, левая ее часть, т.е. 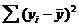 интерпретируется как мера общего разброса или рассеивания переменной y относительно ее среднего значения
интерпретируется как мера общего разброса или рассеивания переменной y относительно ее среднего значения  . Эта мера раскладывается на две составляющие. Первая часть
. Эта мера раскладывается на две составляющие. Первая часть  − это мера разброса, «объясненная» с помощью уравнения регрессии. Вторая часть
− это мера разброса, «объясненная» с помощью уравнения регрессии. Вторая часть 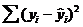 − это мера разброса, «не объясненного» уравнением регрессии. Слова «объясненный» и «не объясненный» взяты в кавычки, так как объяснение, в сущности, может оказаться мнимым. В действительности y может зависеть от какой-то другой переменной z, и x может действовать как величина, заменяющая z.
− это мера разброса, «не объясненного» уравнением регрессии. Слова «объясненный» и «не объясненный» взяты в кавычки, так как объяснение, в сущности, может оказаться мнимым. В действительности y может зависеть от какой-то другой переменной z, и x может действовать как величина, заменяющая z.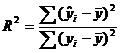 , или
, или 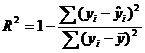 .
.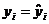 для всех наблюдений, и все остатки равны нулю. Если же в выборке отсутствует видимая связь между y и x, то
для всех наблюдений, и все остатки равны нулю. Если же в выборке отсутствует видимая связь между y и x, то 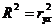 .
. о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fнаб и критического (табличного) Fтаб значений F-статистики Фишера. Если Fтаб < Fнаб то гипотеза
о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fнаб и критического (табличного) Fтаб значений F-статистики Фишера. Если Fтаб < Fнаб то гипотеза  .
.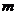 =1, поэтому
=1, поэтому 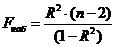 .
.


