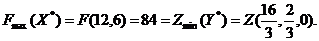1.1. Формулировка классической з адачи линейного программирования
Если все ограничения на переменные в математической модели представляют из себя линейные алгебраические неравенства (равенства), а целевая функция является линейным функционалом относительно переменных модели, то такая математическая модель относится по классификации к теории линейного программирования.
В задачах линейного программирования требуется найти экстремум (максимум или минимум в зависимости от содержательной постановки задачи) линейной функции
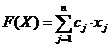
Эта функция, называемая целевой, неограниченна, и поэтому искать ее максимум или минимум, не налагая никаких ограничений на область изменения вектора Х с компонентами 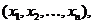 бессмысленно. Интерес представляет задача максимизации этой функции при условии, что вектор Х принадлежит некоторому множеству, причем выбор значений вектора Х определяется условиями типа линейных неравенств.
бессмысленно. Интерес представляет задача максимизации этой функции при условии, что вектор Х принадлежит некоторому множеству, причем выбор значений вектора Х определяется условиями типа линейных неравенств.
В общем случае задача линейного программирования формулируется следующим образом: найти величину вектора Х, доставляющего максимум линейной функции 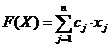
на множестве значений  удовлетворяющих ограничениям вида
удовлетворяющих ограничениям вида
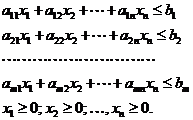
В более компактной форме:
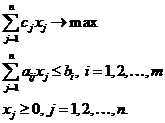
Вектор  называется вектором ограничений для задачи линейного программирования. Вектор
называется вектором ограничений для задачи линейного программирования. Вектор 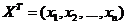

, удовлетворяющий линейным ограничениям, называется допустимым решением задачи линейного программирования. Допустимый вектор Х, доставляющий максимум целевой функции, называется оптимальным решением задачи линейного программирования. Коэффициенты  составляют условия задачи и трактуются исходя из содержательной постановки проблемы.
составляют условия задачи и трактуются исходя из содержательной постановки проблемы.
1. 2. Задача о выпуске продукции
Рассмотрим некоторую производственную систему, в которой m ресурсов S1, S2,…, Sm участвуют в производственном процессе (сырье, топливо, материалы, инструменты и т.д.). Продукты производятся или потребляются с помощью линейных или технологических процессов. Линейная модель производства, в которой участвуют m ресурсов, состоит из набора технологических процессов P1, P2,…, Pn. Она полностью описывается числами aij, где aij – количество ресурса Si, потребляемого при aij> 0 или производимого при aij< 0 при единичной интенсивности использования процесса Pj. Под интенсивностью процесса Pj понимается такое число xj, если в результате работы этого процесса потреблено aij xj единиц ресурса Si. Через cj обозначим доход от реализации единицы продукции, получаемой при использовании процесса Pj с единичной интенсивностью. В более простой интерпретации в качестве P1, P2,…, Pn можно рассматривать список производимой продукции. Запасы ресурсов каждого вида ограничены и равны b1, b2,…, bm. Требуется определить, в каком количестве выпускать продукцию каждого вида, чтобы доход от реализации этой продукции был максимален с учетом ограничений на ресурсы. Другими словами нужно определить производственный план. Общий доход от реализации выпущенной продукции будет равен 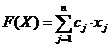 .
.
Ограничениями в этой задаче являются требования, чтобы расход ресурсов вида Si на выпуск всех видов продукции не превышал имеющихся запасов 
Пример 1. Некоторому заводу требуется составить оптимальный производственный план выпуска двух видов изделий при определенных возможностях трех типов машин. План выпуска должен быть таким, чтобы от реализации выпущенной по этому плану продукции завод получил бы наибольшую прибыль. Оба вида изделий последовательно обрабатываются этими машинами (см. таб.1). Завод от реализации одного изделия первого вида получает 4 тыс. рублей, а от реализации одного изделия второго вида 6 тыс. рублей прибыли.
Таблица 1
| Виды машин
Виды изделий
| Первый
| Второй
| Третий
|
| Первое изделие
| 0,5
| 2
| 0
|
| Второе изделие
| 1
| 1
| 1
|
| Время работы машин
| 12
| 30
| 9
|
Построим математическую модель этой задачи. Пусть х1число изделий первого вида, а х2– число изделий второго вида.
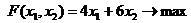
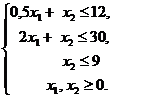
Вместе с исходной (прямой) задачей рассматривается двойственная к ней задача, которую можно сформулировать следующим образом.
Предположим, что некоторая организация решила закупить ресурсы S1, S2,…, Sm фирмы и необходимо определить цены на эти ресурсы у1, у2,…, у m. Естественно, что покупающая организация заинтересована в том, чтобы затраты на покупку ресурсов в объеме b 1, b 2,…, bm по ценам у1, у2,…, у m были минимальны, то есть
Z = b1y1 + b2y2 + … +bmym ® min.
Предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не меньше той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции j-го вида расходуется сырье S1 в объеме а1 j, сырье S2 в объеме а2 j …, сырье Sm в объеме а mj по цене у1, у2,…, у m соответственно, то есть затраты на изготовление продукции Pj должны быть не меньше, чем цена ее реализации. Приходим к ограничениям следующего вида:
а1 j у1 + а2 j у2 + … + а mj у m ≥ с j, j =1,2,..., n.
Учитывая условия неотрицательности цены единицы i-го ресурса, приходим к следующей задаче:
Найти такой вектор Y = (у1, у2 ,..., у m) – цен ресурсов, удовлетворяющий системе неравенств
 a11 у 1 + a21 у 2 + … + am1 у m ≥ c1,
a11 у 1 + a21 у 2 + … + am1 у m ≥ c1,
a12y1 + a22y2 + … + am2ym ≥ c2,
… … … … … … …
a1jy1 + a2jy2 + … + amjym ≥ cj,
… … … … … … …
a1ny1 + a2ny2 + … + amnym ≥ cn,
yi ³ 0, i = 1, 2, …, m,
при котором функция Z (Y) = b 1 y 1 + b 2 y 2 + …+ bmym принимает минимальное значение.
Цены ресурсов в экономической литературе имеют различные названия: учетные, неявные, теневые, объективно-обусловленные оценки (о-о оценки). Смысл этих названий состоит в том, что это условные (ненастоящие) цены. Эти цены определяются в ходе решения задачи, их называют еще ценностью ресурсов.
Пример 2. Построим двойственную задачу к прямой задаче из примера 1.
Пусть y 1 – ценность первого ресурса, y 2 – ценность второго ресурса, а y 3 – ценность третьего ресурса. Тогда
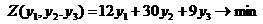
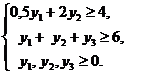
Сопоставим общие представления прямой и двойственной задач в табл. 2, причем прямая задача – это задача модели распределения ограниченных ресурсов.
Таблица 2
| Прямая задача
| Двойственная задача
|
Максимизировать F = 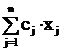 при ограничениях
при ограничениях
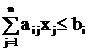 ; i=1,2,...,m
xj ³ 0, j = 1, 2, …, n, ; i=1,2,...,m
xj ³ 0, j = 1, 2, …, n,
| Минимизировать Z = 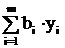 при ограничениях
при ограничениях
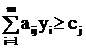 ; j = 1, 2, …, n
yi ³ 0, i=1,2,...,m ; j = 1, 2, …, n
yi ³ 0, i=1,2,...,m
|
Сравнивая рассмотренные примеры видно, что двойственная задача по отношению к исходной составляется согласно следующим правилам:
1. Если первая задача имеет размеры  (m–ограничений с n неизвестными), то вторая – размеры
(m–ограничений с n неизвестными), то вторая – размеры 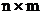 .
.
2. Матрицы из коэффициентов при неизвестных в левых частях ограничений обеих задач являются взаимно транспонированными.
3. В правых частях ограничений в каждой задаче стоят коэффициенты при неизвестных в целевой функции другой задачи.
4. В прямой задаче все ограничения представляют собой неравенства типа « », причем в этой задаче требуется достичь
», причем в этой задаче требуется достичь 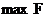 . Напротив, в двойственной задаче все ограничения суть неравенства типа «
. Напротив, в двойственной задаче все ограничения суть неравенства типа « », причем требуется достичь
», причем требуется достичь  .
.
Если в задаче линейного программирования число переменных равно двум, то ее можно решить графическим методом. Суть метода состоит в следующем. Решением системы ограничений задачи является совокупность точек плоскости, координаты которых удовлетворяют каждому из неравенств системы. Эта совокупность может образовывать некоторую фигуру на плоскости, в качестве которой может быть некоторый многоугольник, либо некоторая неограниченная область, либо вообще пустое множество. Она называется допустимой областью. На этой области мы должны найти экстремум целевой функции. Известно, что этот экстремум достигается на границе области. Поиск этой граничной точки и составляет суть метода. Поясним это на примере.
Пример 3. Решим графическим методом задачу ЛП из примера 1.
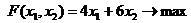
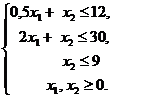
Решением линейного алгебраического неравенства относительно двух переменных является совокупность точек плоскости, координаты которых удовлетворяют этому неравенству. Графически – это полуплоскость. Решением системы таких неравенств является их пересечение. Для нахождения такой полуплоскости необходимо знак неравенства заменить на знак равенства, построить соответствующую этому уравнению прямую на плоскости и выбрать из двух образовавшихся полуплоскостей нужную.
В прямоугольной декартовой системе координат (рис. 1.1.) строим прямую 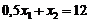 , соответствующую ограничению (1) по двум точкам, например, (24; 0) и (0; 12). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая не проходит через начало координат, подставляем координаты точки
, соответствующую ограничению (1) по двум точкам, например, (24; 0) и (0; 12). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая не проходит через начало координат, подставляем координаты точки  в первое ограничение
в первое ограничение 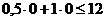 . Получаем строгое неравенство
. Получаем строгое неравенство 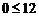 . Следовательно, точка О лежит в полуплоскости решений. Штриховкой отмечаем полуплоскость, содержащую точку О. Аналогично строим прямую
. Следовательно, точка О лежит в полуплоскости решений. Штриховкой отмечаем полуплоскость, содержащую точку О. Аналогично строим прямую  по двум точкам (0;30) и (15; 0) и определяем область решений ограничения (2). Третья прямая будет параллельна оси
по двум точкам (0;30) и (15; 0) и определяем область решений ограничения (2). Третья прямая будет параллельна оси 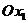 .
.
Построим на плоскости область допустимых решений. Находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности переменных.
х2



 D C
D C


 B
B



 A
A
 O F=0 15 24 х1
O F=0 15 24 х1
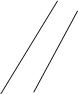
Рис. 1.1. Графическое решение задачи
Множество допустимых решений представляет собой многоугольник ОАВСD (рис. 1.1). Среди точек многоугольника ОАВСD найдем оптимальную.
Строим нормаль линий уровня  . Так как решается задача на отыскание максимума целевой функции, то линию уровня
. Так как решается задача на отыскание максимума целевой функции, то линию уровня 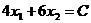 перемещаем в направлении нормали до угловой точки В, которая расположена на прямой, называемой опорной. Эта опорная прямая проходит через точку В пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (2), перпендикулярно нормали.
перемещаем в направлении нормали до угловой точки В, которая расположена на прямой, называемой опорной. Эта опорная прямая проходит через точку В пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (2), перпендикулярно нормали.
В этой точке пересекаются две прямые:
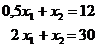
Найдем координаты точки В:


Полученное решение будет оптимальным производственным планом, дающим заводу максимальную прибыль, а именно, 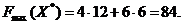
В двойственной задаче из примера 2 уже три неизвестных величины. Поэтому такую задачу ЛП мы уде не модем решить графическим методом. В этом случае, так как у нас есть уже решение прямой задачи, мы можем воспользоваться следующей теоремой.
Теорема равновесия. Пусть Х* – какое-нибудь допустимое решение прямой задачи, а Y * – какое-нибудь допустимое решение двойственной задачи. Для одновременной оптимальности этих решений необходимо и достаточно выполнение равенств:
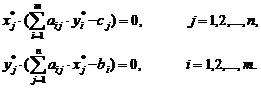
Величины, стоящие в скобках сформулированной теоремы, равны разности между левой и правой частями ограничения одной из двойственных задач на соответствующую переменную другой задачи.
Применим теорему равновесия для решения задачи из примера 2.
Пример 4. Запишем прямую и двойственную задачу в таблицу
| Прямая задача
| Двойственная задача
|
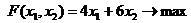 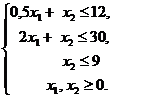
| 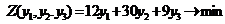 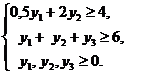
|
Тогда теорема равновесия запишется в виде:
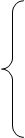
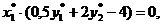


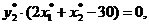
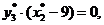
Третье ограничение прямой задачи на оптимальном плане выполняется как строгое неравенство, следовательно, соответствующая переменная двойственной задачи равна нулю: y3*= 0.
Первое и второе ограничение прямой задачи обращается в точное равенство, следовательно, соответствующие переменные двойственной задачи положительны: y1* > 0 и y2* > 0.
Условия равновесия можно записать в виде равенств:

Подставляя y3*=0 в последнюю систему уравнений, получим систему:
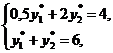
откуда получаем, что y1* =  , y2*=
, y2*= 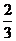 .
.
Оптимальное решение двойственной задачи Y * = ( ;
; 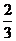 ; 0), при этом минимум целевой функции двойственной задачи: Zmin = Z(Y*) = 12·
; 0), при этом минимум целевой функции двойственной задачи: Zmin = Z(Y*) = 12·  +30·
+30· 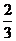 =84.
=84.
Существует определенная связь между значениями целевых функций прямой и двойственной задачи на допустимых решениях. Она определяется следующими теоремами теории двойственности:
Теорема (основное неравенство). Пусть Х – какое-нибудь допустимое решение прямой задачи, а Y – какое-нибудь допустимое решение двойственной задачи. Тогда справедливо неравенство 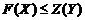 .
.
Следствие 1 (достаточный признак оптимальности). Если для каких-то допустимых решений 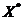 и
и  соответственно прямой и двойственной задач выполняется равенство
соответственно прямой и двойственной задач выполняется равенство 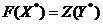 , то
, то 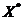 есть оптимальное решение прямой задачи, а
есть оптимальное решение прямой задачи, а  – оптимальное решение двойственной задачи.
– оптимальное решение двойственной задачи.
Следствие 2. Если в одной из пары двойственных задач целевая функция не ограничена с соответствующей стороны (т.е. 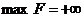 в прямой задаче или
в прямой задаче или 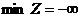 в двойственной задаче), то другая задача не имеет допустимых решений.
в двойственной задаче), то другая задача не имеет допустимых решений.
Основная теорема. Если разрешима одна из пары двойственных задач, то разрешима и другая задача, причем  .
.
Действительно, для разобранных в примерах задачах мы получили соотношение
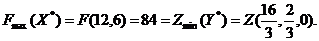



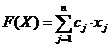
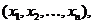 бессмысленно. Интерес представляет задача максимизации этой функции при условии, что вектор Х принадлежит некоторому множеству, причем выбор значений вектора Х определяется условиями типа линейных неравенств.
бессмысленно. Интерес представляет задача максимизации этой функции при условии, что вектор Х принадлежит некоторому множеству, причем выбор значений вектора Х определяется условиями типа линейных неравенств. удовлетворяющих ограничениям вида
удовлетворяющих ограничениям вида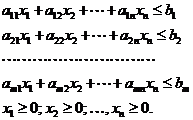
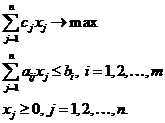
 называется вектором ограничений для задачи линейного программирования. Вектор
называется вектором ограничений для задачи линейного программирования. Вектор 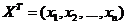

 составляют условия задачи и трактуются исходя из содержательной постановки проблемы.
составляют условия задачи и трактуются исходя из содержательной постановки проблемы.
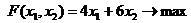
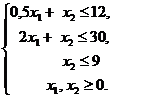
 a11 у 1 + a21 у 2 + … + am1 у m ≥ c1,
a11 у 1 + a21 у 2 + … + am1 у m ≥ c1,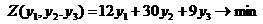
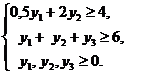
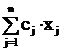 при ограничениях
при ограничениях
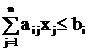 ; i=1,2,...,m
xj ³ 0, j = 1, 2, …, n,
; i=1,2,...,m
xj ³ 0, j = 1, 2, …, n,
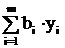 при ограничениях
при ограничениях
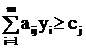 ; j = 1, 2, …, n
yi ³ 0, i=1,2,...,m
; j = 1, 2, …, n
yi ³ 0, i=1,2,...,m
 (m–ограничений с n неизвестными), то вторая – размеры
(m–ограничений с n неизвестными), то вторая – размеры 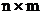 .
. », причем в этой задаче требуется достичь
», причем в этой задаче требуется достичь 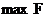 . Напротив, в двойственной задаче все ограничения суть неравенства типа «
. Напротив, в двойственной задаче все ограничения суть неравенства типа « », причем требуется достичь
», причем требуется достичь  .
.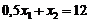 , соответствующую ограничению (1) по двум точкам, например, (24; 0) и (0; 12). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая не проходит через начало координат, подставляем координаты точки
, соответствующую ограничению (1) по двум точкам, например, (24; 0) и (0; 12). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая не проходит через начало координат, подставляем координаты точки  в первое ограничение
в первое ограничение 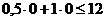 . Получаем строгое неравенство
. Получаем строгое неравенство 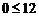 . Следовательно, точка О лежит в полуплоскости решений. Штриховкой отмечаем полуплоскость, содержащую точку О. Аналогично строим прямую
. Следовательно, точка О лежит в полуплоскости решений. Штриховкой отмечаем полуплоскость, содержащую точку О. Аналогично строим прямую  по двум точкам (0;30) и (15; 0) и определяем область решений ограничения (2). Третья прямая будет параллельна оси
по двум точкам (0;30) и (15; 0) и определяем область решений ограничения (2). Третья прямая будет параллельна оси 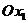 .
.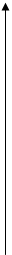




 D C
D C


 B
B


 A
A O F=0 15 24 х1
O F=0 15 24 х1 . Так как решается задача на отыскание максимума целевой функции, то линию уровня
. Так как решается задача на отыскание максимума целевой функции, то линию уровня 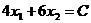 перемещаем в направлении нормали до угловой точки В, которая расположена на прямой, называемой опорной. Эта опорная прямая проходит через точку В пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (2), перпендикулярно нормали.
перемещаем в направлении нормали до угловой точки В, которая расположена на прямой, называемой опорной. Эта опорная прямая проходит через точку В пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (2), перпендикулярно нормали.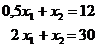


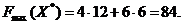
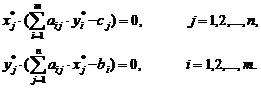
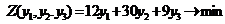
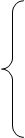
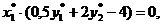


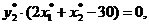
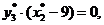

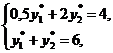
 , y2*=
, y2*= 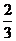 .
.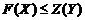 .
.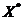 и
и  соответственно прямой и двойственной задач выполняется равенство
соответственно прямой и двойственной задач выполняется равенство 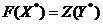 , то
, то 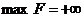 в прямой задаче или
в прямой задаче или 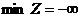 в двойственной задаче), то другая задача не имеет допустимых решений.
в двойственной задаче), то другая задача не имеет допустимых решений. .
.