Генерация СЛАУ для глобальной задачи

После получения всех многомасштабных базисных функций (локальных на каждом макроэлементе) согласно алгоритму многомасштабного метода [10] необходимо построить общую вариационную формулировку и вычислить элементы матрицы жесткости.

С учетом перепишем глобальную постановку в виде системы линейных алгебраических уравнений:

 

   

 

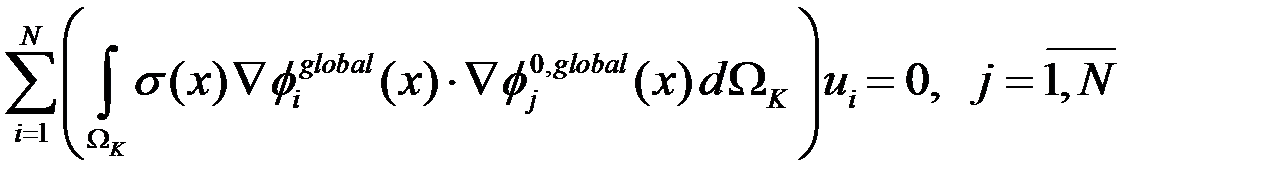
Если записать СЛАУ в матричном виде, то получим аналогично -:

 

                                                                            

 

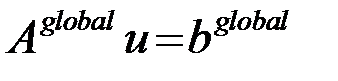
Компоненты матрицы и правая часть могут быть определены следующим образом:

 

,   

                          ,                            

 

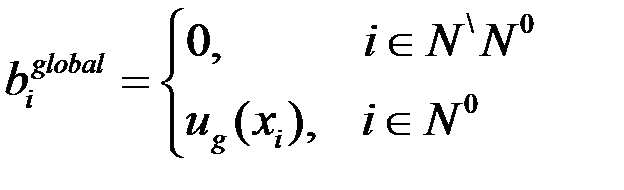где 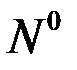 - узлы грубой сетки, в которых заданы первые краевые условия. Под  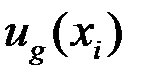будем понимать значение искомой функции на границе области моделирования, где задано первое краевой условие.

Рассмотрим более подробно 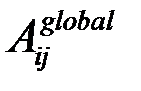, когда .

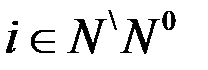С учетом конечноэлементного разбиения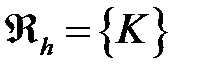

 

   

 

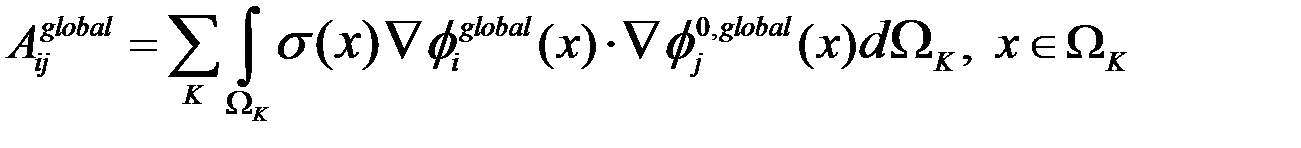
Введем матрицу 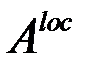как локальную матрицу, соответствующую конечному элементу 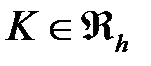. Для того, чтобы определить локальные функции на элементе введем локальную нумерацию, представленную на рисунке 7

                  

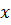
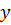
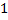
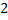
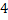
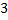
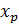
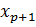
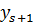
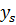
Рисунок 7 – Локальная нумерация узлов в конечном элементе.

 

Очевидно, что на элементе 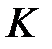 ненулевыми будут только четыре функции  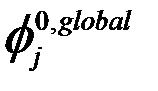и четыре 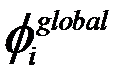. Обозначим их как  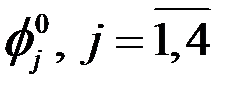 и 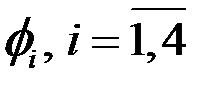, причем функция с номером i равна единице в i-ом узле и нулю во всех остальных. Запишем соотношение для одного конечного элемента, причем, будем считать, что на элементе электропроводность равна некоторому среднему значению :

 

                               

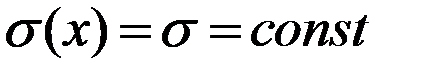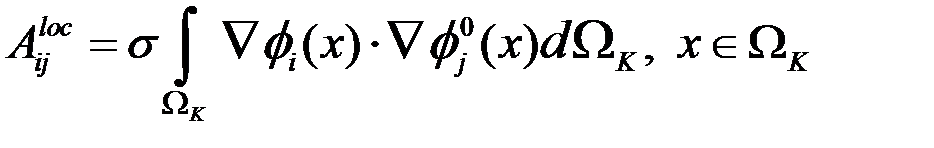
Вычисление элементов матрицы A будем проводить в идеологии двухуровневых методов [25, 27]. Каждая локальная функция 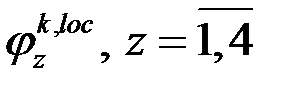, определенная на элементе  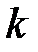мелкого разбиения текущего макроэлемента  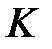может быть представлена в виде:

 

                            .                              

 

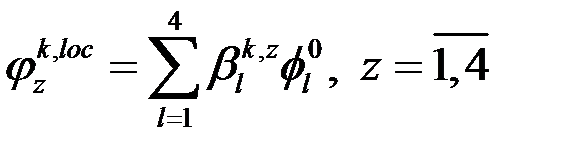Тогда и локальная многомасштабная функция 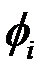 может быть определена как

                                                                    

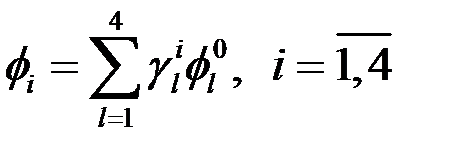
Введем обозначения, представленные на рисунке 8:

     

 

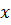
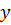
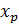
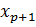
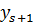
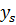
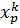
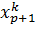
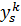
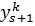
Рисунок 8 – Обозначения координат элемента 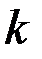 мелкого разбиения .

 

Заштрихованный прямоугольник соответствует элементу мелкого разбиения .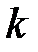

Для нахождения 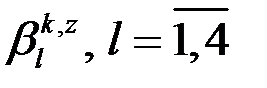 из необходимо решить СЛАУ вида:

 

                                                                                    

 

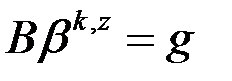
Матрица 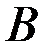 и вектор правой части  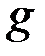в системе определены следующим образом:

 

 

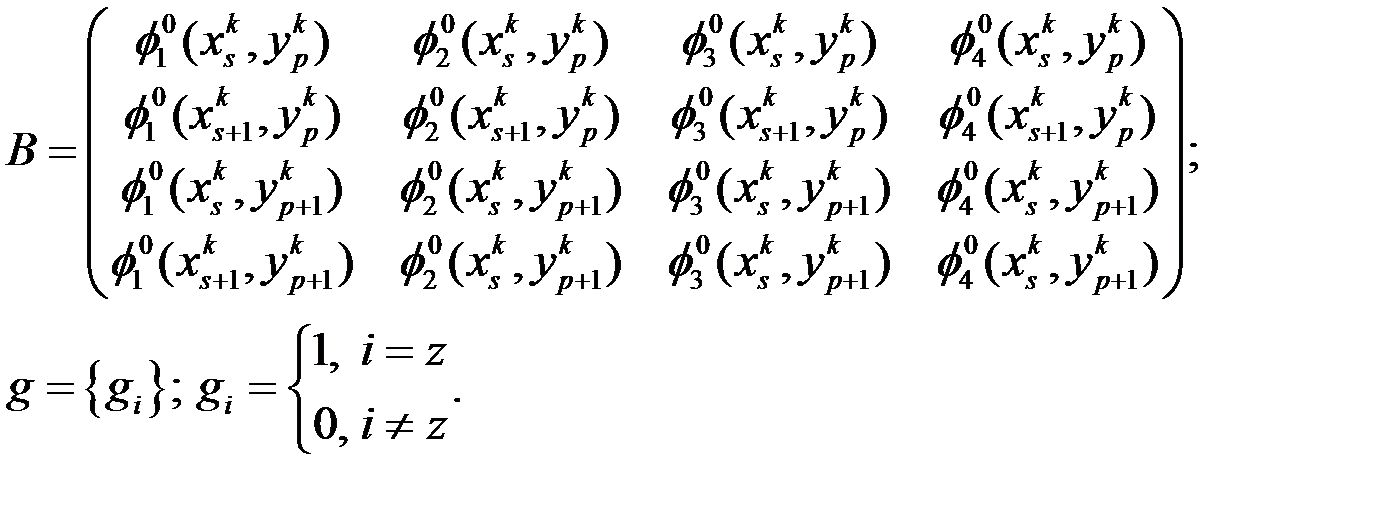
Для нахождения 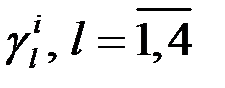  из подставим представление:

                

 

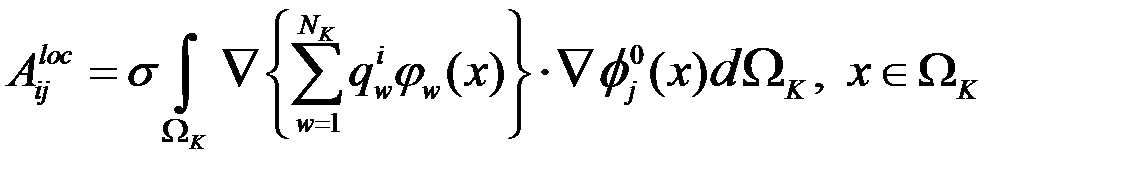
С учетом мелкого разбиения 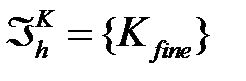 на макроэлементе:

 

 

 

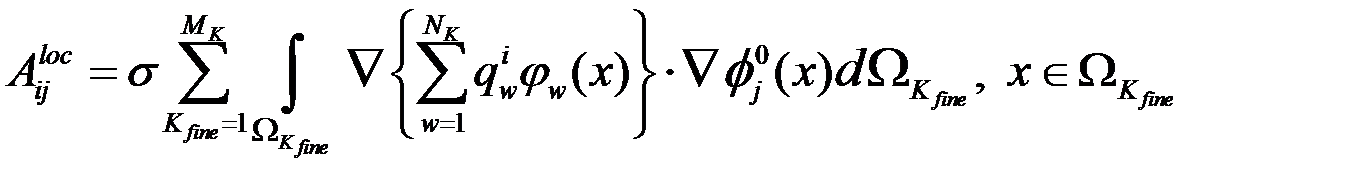
где 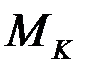 - количество элементов в разбиении .

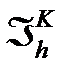Так как на каждом элементе 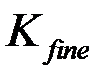 ненулевые только четыре базисные функции, то перепишем соотношение.

 

 

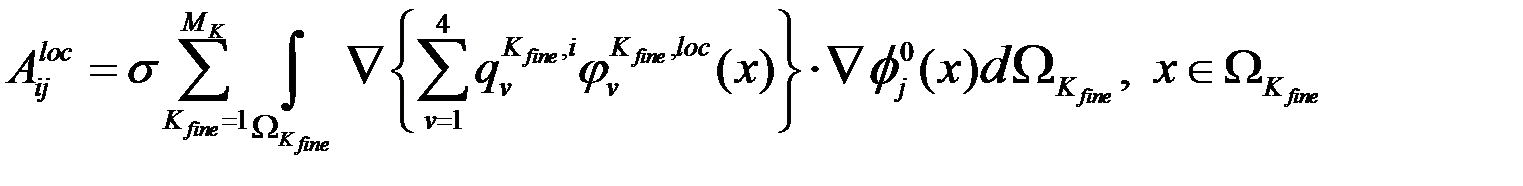
Учитывая представление:

 

 

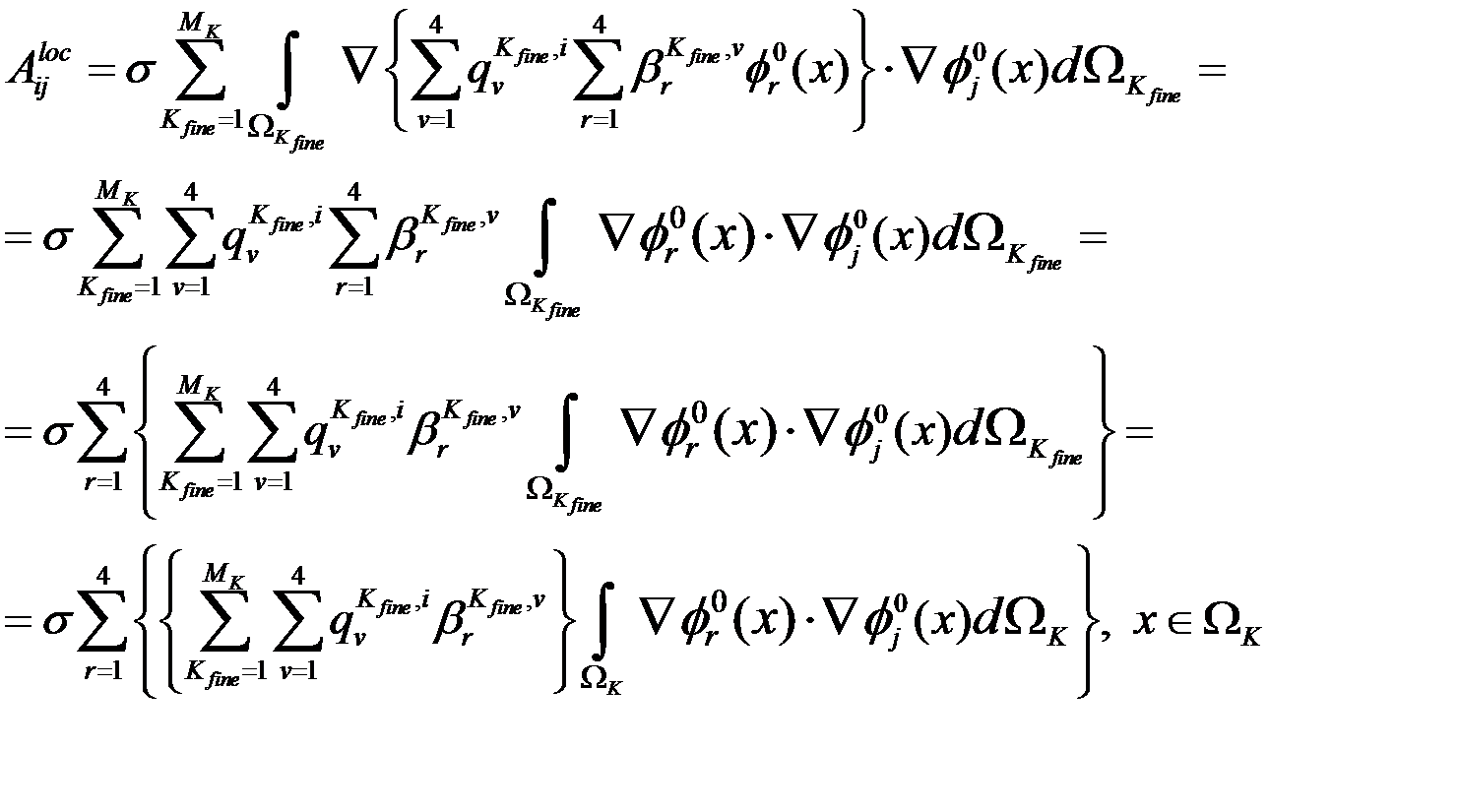
Таким образом получаем соотношение для нахождения 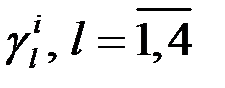  из:

 

                                    

 

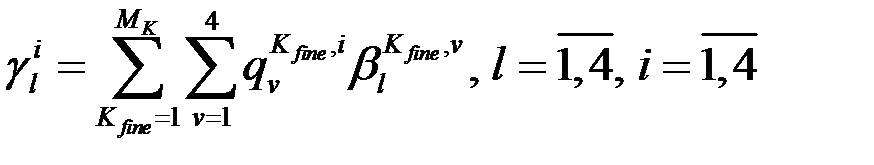
Как уже говорилось ранее, в качестве 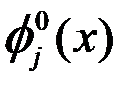 выбираются стандартные билинейные базисные функции, которые с учетом введенных обозначений на рисунках 7 и 8 имеют вид:

 

                 

 

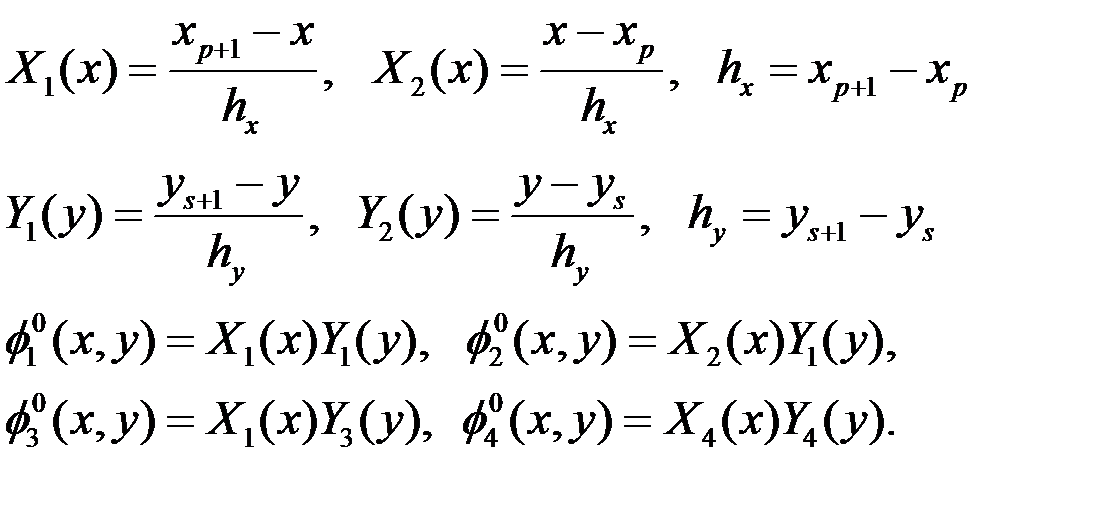
Так как получили, что матрица 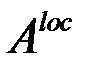 состоит из сумм интегралов от произведения градиентов стандартных базисных функций, то удобно воспользоваться уже известными соотношениями для матрицы жесткости [28]:

 

 

С учетом получаем выражение для вычисления матрицы :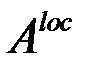

 

                                                                        

 

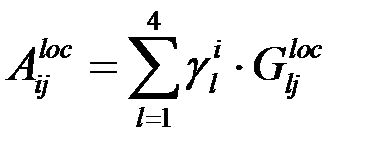
После вычисления локальных матриц используется стандартная процедура сборки глобальной матрицы 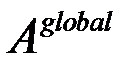 для СЛАУ, но в отличие от Галеркинской постановки получаем несимметричную матрицу. После учета краевых условий необходимо решить систему. Для этого в данной работе использовался метод BSGStab с LU предобуславливанием [17, 32].

Вывод решения.

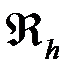
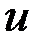Решив систему, получаем вектор   , компоненты которого являются значениями скалярного потенциала в узлах грубой сетки     . Однако чаще всего необходимо знать решение не только в узлах сетки, но и в каждой точке области моделирования.

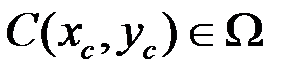Для того чтобы определить значение скалярного потенциала в точке           апрапрапаапра, можно воспользоваться следующим алгоритмом:

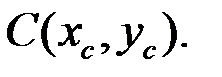
1. 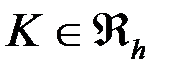Определить к какому элементу               принадлежит точка

 

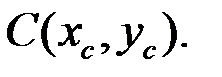
2. 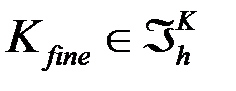Определить к какому элементу              принадлежит точка

 

3. 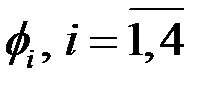Для каждой многомасштабной     функции найти: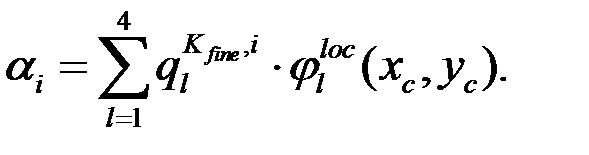

4. Вычислить значение потенциала по формуле: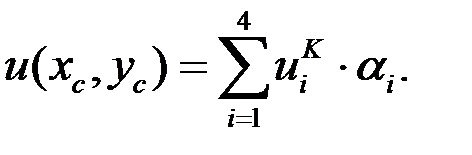

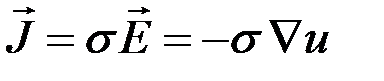Еще бывает необходимо знать значения векторных величин, например, плотности тока:                          . Найдем плотность тока в точке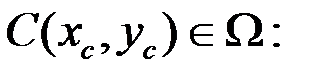

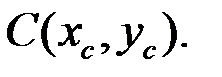
1. 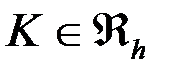Определить к какому элементу           принадлежит точка

 

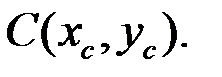
2. 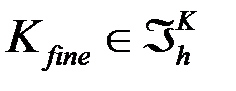Определить к какому элементу            принадлежит точка

 

3. 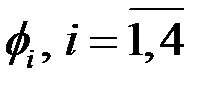Для каждой многомасштабной функции    найти: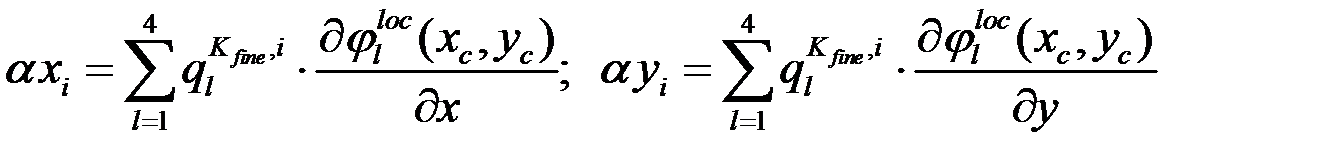

4.

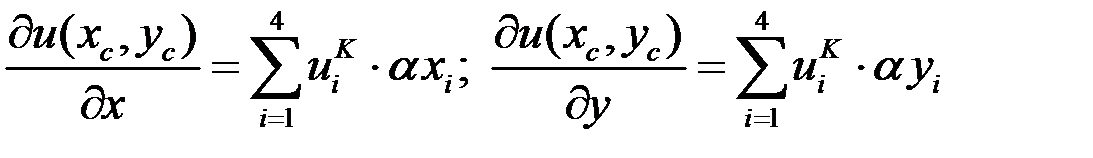
5. Отсюда получаем плотность тока:

 

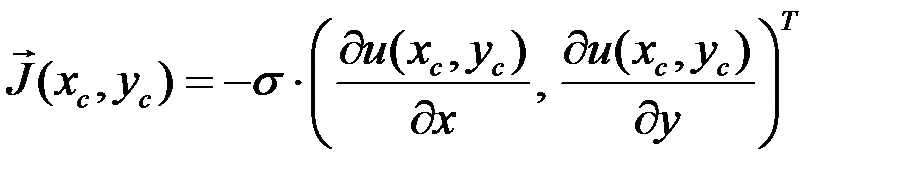
Эффективное сопротивление.

При исследовании гетерогенных сред было обнаружено, что в объемах превышающих объем одного включения проявляются устойчивые физические характеристики (например, теплопроводность электропроводность), в общем случае отличающимися от характеристик отдельных компонент. Такие характеристики среды называют эффективными [23,10,15].

Определение эффективного удельного электрического сопротивления гетерогенной среды осуществляется следующим образом [33]:

 

                                                    ,                                                        

 

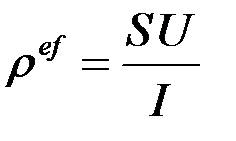где S  – площадь сечения, перпендикулярного течению тока исследуемого образца, U    – разность потенциалов, I  – полный ток в образце, определяемый по формуле

 

                                                                                                          

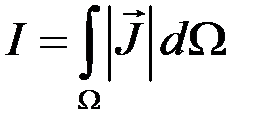
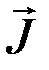
где – плотность тока.

Верификация

Верификацию программного комплекса будем производить в области с небольшим количеством включений.

Сформулируем задачу:

 

                                                                                                  

 

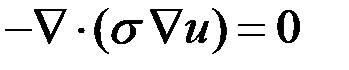
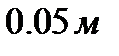В качестве расчетной области возьмем прямоугольную область  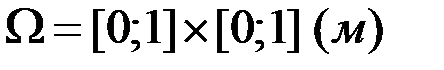  вапрапрапрапренгап(рисунок 9).

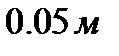
Рисунок 9 – Область моделирования      с грубой сеткой

 

На границах заданы краевые условия (рисунок 3):

                                                                                                  

 

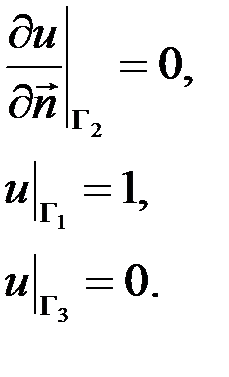
Электропроводность определяется следующим образом:

 

                                 

 

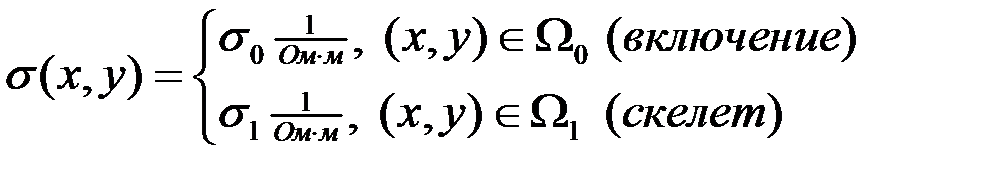
СЛАУ решается с фиксированной точность 10^-8.

Относительную погрешность будем оценивать по формуле:

 

                       ,                           

 

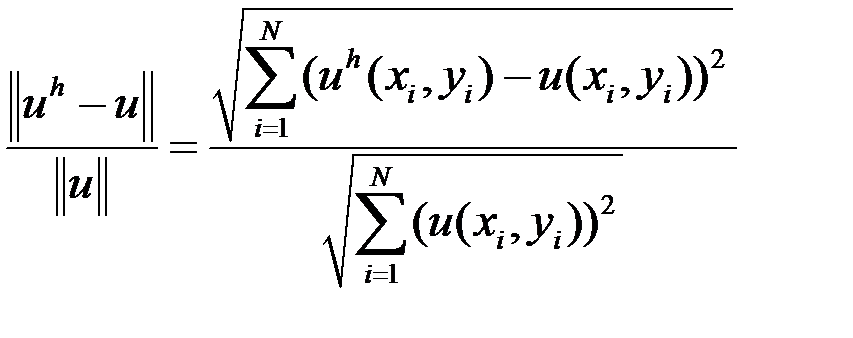где 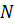 – количество рассматриваемых точек,  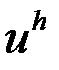– полученное решение,  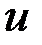– точное решение.

Пусть 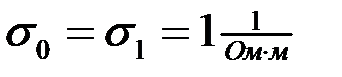, тогда задача с краевыми условиями имеет аналитическое решение

 

                                                                                                            

 

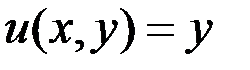
В таблице 1 приведены относительные погрешности решения, полученного МКЭ [28] и многомасштабным МКЭ.

 

 

Таблица 1 – Сравнение полученных решений и точного решения

По прямой  при	1.4200E-08	1.0443E-08

 

Если 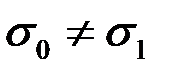, то задача с краевыми условиями не имеет аналитического решения и результаты, полученные многомасштабным МКЭ будем сравнивать с результатами классического МКЭ на подробной сетке. Пусть 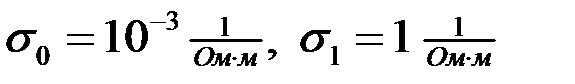, т.е. включения непроводящие. Результаты моделирования приведены на рисунке 10 и в таблице 2

 

 

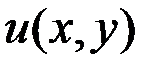
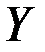
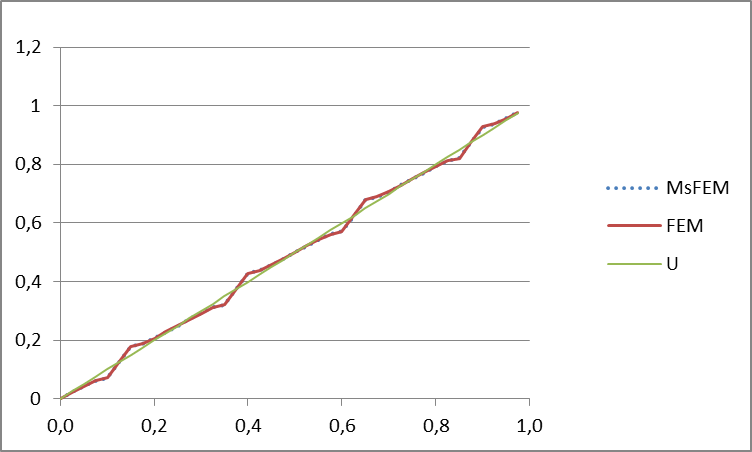
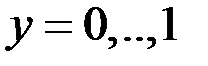
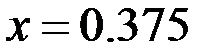Рисунок 10 – Значения скалярного потенциала на прямой               при   арварарр(проходит через центры включений)

 

Таблица 2 – Числовые характеристики решения на вложенных сетках

В узлах грубой сетки	2.51E-08	1.72E-08
На прямой x=0.375	8.51E-04	2.61E-04
На прямой y=0.375	4.98E-04	5.05E-04

 

На рисунке 11 изображено распределение скалярного потенциала. На рисунке 12 - векторное поле плотности тока.

 

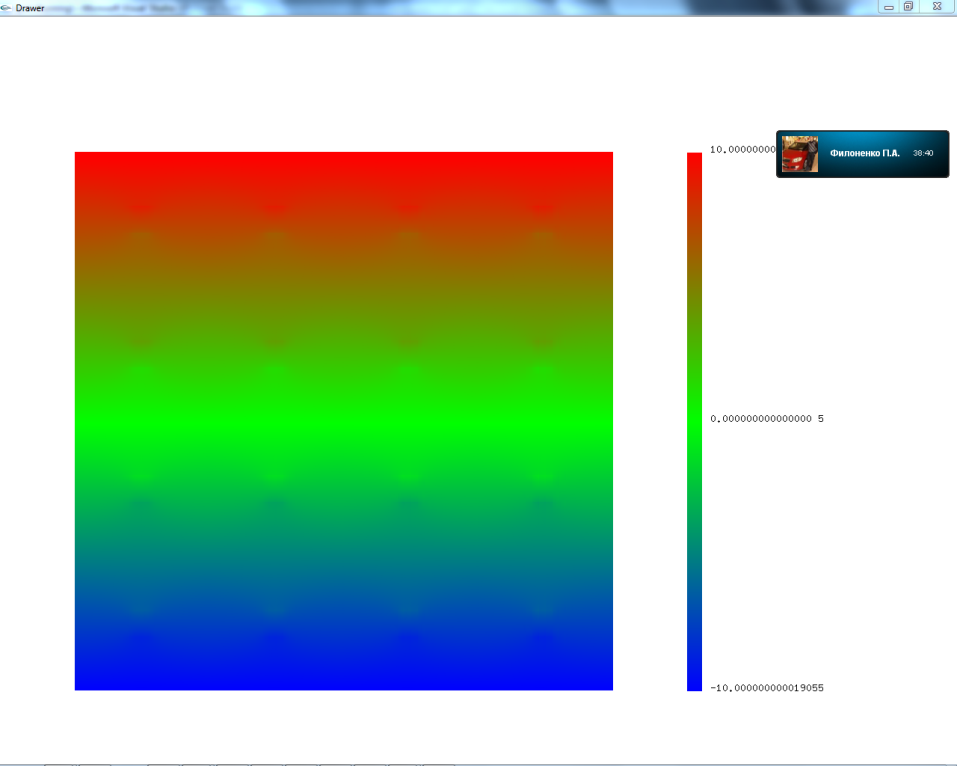
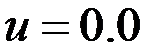
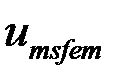
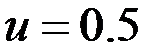
Рисунок 11– Распределение скалярного потенциала  апрапр

 

Рисунок 12 – Векторное поле плотности тока

 

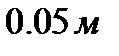
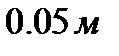
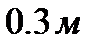Рассмотрим задачу - в области  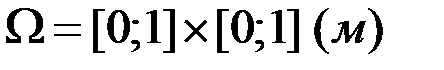                                   (рисунок 13)

 

 

Рисунок 13 – Область моделирования     с грубой сеткой

 

В данной области включения пересекают границы грубых элементов, поэтому необходимо использовать осциллирующие краевые условия. Вид базисной функции для данной области на рисунке 6. Причем в тех макроэлементах, где нет включений, можно многомасштабные базисные функции не строить.

Результаты моделирования приведены на рисунках 14 и 15.

 

 

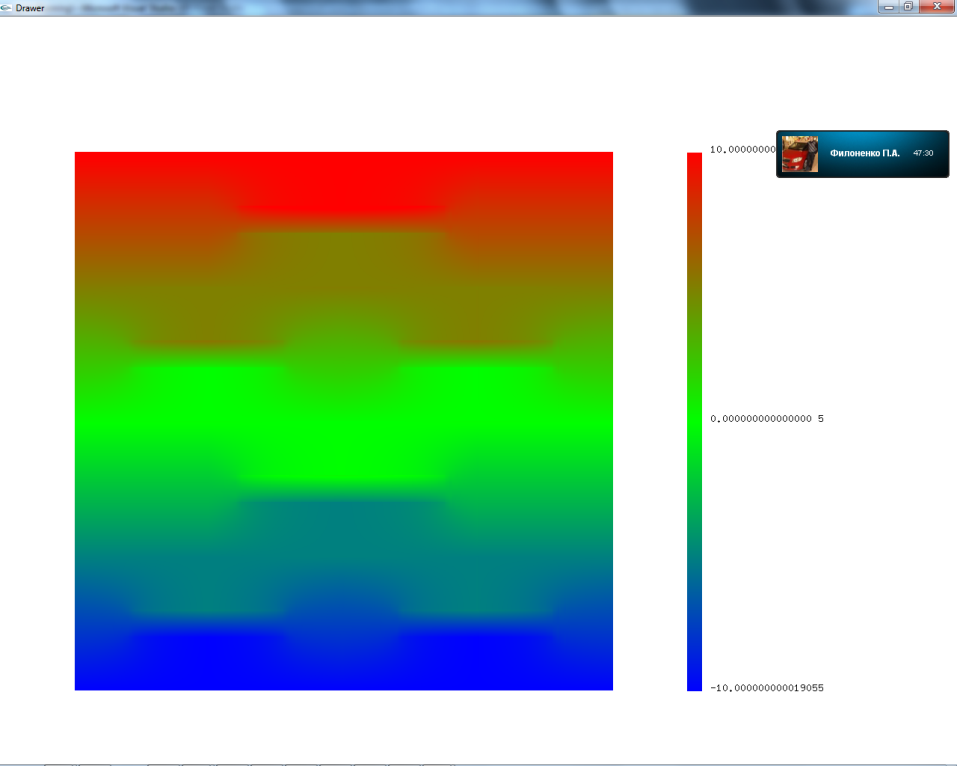
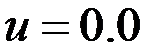
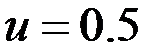
Рисунок 14 – Распределение скалярного потенциала

Рисунок 15 – Векторное поле плотности тока

Результаты моделирования