Аннотация
В данной работе исследуется многомасштабный метод конечных элементов и материалы с включениями, имеющими контрастные электрические свойства.
Целью работы является реализация алгоритма многомасштабного метода конечных элементов.
В процессе работы были рассмотрены различные вычислительные схемы на основе МКЭ и многомасштабного МКЭ и реализованы алгоритм многомасштабного МКЭ и визуализатор, для удобства анализа получаемых результатов.
В результате исследования было получено электрическое поле в прямоугольной расчетной области с включениями и были рассчитаны значения эффективного сопротивления для разных материалов.
Annotation
Text. Text. Text.
Содержание
Введение 5
1. Математическая модель 9
1.1. Уравнения Максвелла 9
1.2. Условия на контактных границах 11
2. Постановка задачи 12
3. Вариационная постановка 13
4. Дискретная вариационная постановка 15
5. Многомасштабный метод конечных элементов 16
5.1. Многомасштабные базисные функции 20
5.2. Краевые условия для многомасштабных базисных функций 23
5.3. Генерация СЛАУ для глобального решения 26
5.4. Вывод решения 32
6. Эффективное сопротивление 34
7. Верификация 35
8. Результаты моделирования 41
8.1. Изменение количества включений 41
8.2. Изменение количества макроэлементов 43
8.3. Расчет эффективного сопротивления 45
9. Экономический расчёт 47
Заключение 48
Список литературы 49
Приложение А. ММКЭ 52
Приложение Б. МКЭ 75
Приложение С. Визуализатор 78
Приложение D. Техника безопасности 80
Введение
Значительной части прикладных задач свойственна многомасштабность и многофизичность. Одним из примеров является исследование свойств сложных гетерогенных сред, например, композитных материалов, горных пород, смесей проводящих и непроводящих частиц и др.
Существует несколько способов исследования таких материалов: лабораторные эксперименты, аналитические оценки, численное моделирование. Существенным ограничением лабораторных экспериментов выступает сложность изготовления образцов и их высокая стоимость. Аналитические оценки достаточно просты и легко применимы, однако их использование возможно не для всех конфигураций сред. Традиционные численные методы также не всегда могут быть использованы, так как необходим учет особенностей гетерогенных сред на всех масштабах, что приводит к значительному увеличению размеров дискретизации, что не всегда возможно в связи с ограниченностью вычислительных ресурсов. Другим путем является упрощение модели, например, рассмотрение задачи меньшей размерности. Поэтому на сегодняшний день разработка численных методов, позволяющих моделировать процессы в таких областях с учетом всех многомасштабных свойств среды является актуальной задачей.
Целью данной работы разработка алгоритмов на базе гетерогенного многомасштабного метода конечных элементов для исследование электростатических свойств гетерогенных сред под действием постоянного тока; Для реализации поставленной цели сформулированы следующие задачи:
1. Разработать алгоритмы для решения задачи о распределении скалярного потенциала под действием постоянного тока;
2. Разработать комплекс программ, реализующих решение однородного эллиптического уравнения в двумерных и трехмерных областях для неструктурированных дискретизаций на прямоугольные, треугольные, паралелепипедальные, тетраэдральные суперэлементы;
3. Провести тестирование разработанного программного комплекса;
4. Сравнить точность и скорость решения задачи различными методами: гетерогенным методом, многомасштабным методом конечных элементов, классическим методом конечных элементов;
5. Исследовать влияние электрофизических и геометрических свойств включений удельное эффективное электрическое сопротивление гетерогенных материалов.
В рамках диссертационных исследований получены следующие результаты:
1. Исследованы особенности построения многомасштабных базисных функций на различных типах макроэлементов;
2. Исследована масштабируемость гетерогенного метода;
3. Произведено сравнение гетерогенного и многомасштабного методов;
4. Исследовано влияние расположения, геометрии и свойств включений на удельное эффективное электрическое сопротивление сред в том числе возникновение преколяции;
5. Создан комплекс программ для решения однородного эллиптического уравнения с краевыми условиями Дирихле и Неймана для гетерогенных сред различной геометрии.
Структура и объем магистерской диссертации
Магистерская диссертация состоит из 5 глав, введения и заключения:
Во введение показана актуальность темы, сформулированы цель и задачи работы.
В главе 1 описана система уравнений Максвелла, приведено эллиптическое уравнение и условия на контактных границах (границах раздела сред).
В главе 2 рассматриваются основные процедуры осреднения гетерогенных сред, приводятся основные аналитические соотношения и рассматривается численный подход, основанный на нахождении распределения скалярного потенциала в области моделирования под действием постоянного тока.
В главе 3 приводится описание и результаты физических экспериментов по нахождению удельного электрического сопротивления гетерогенных сред.
В главе 4 дается обзор существующих методов решения задач электростатики в гетерогенных средах, обосновывается выбор гетерогенного многомасштабного метода на базе метода конечных элементов. Рассматриваются структура метода, особенности построения эффективной матрицы жесткости. Производится сравнение с многомасштабным методом конечных элементов. Так же приводится краткое описание программного комплекса.
В главе 5 приводятся результаты верификации и валидации (сравнение с физическими экспериментами) программного комплекса; исследования о влиянии конфигурации и свойств включений на эффективные свойства гетерогенных материалов.
Заключение содержит основные результаты работы.
Работа содержит 93 страницы, включая 32 рисунка, 16 таблиц и 3 приложения.
Апробация работы
По материалам диссертации опубликованы две статьи [1], [2].
Основные положения диссертации докладывались и были одобрены на следующих конференциях [3-9] [3] [4] [5] [6] [7] [8] [9]:
1. XIII Всероссийская конференция молодых ученых по математическому моделированию и информационным технологиям (Новосибирск, 2012). Тезисы опубликованы.
2. Всероссийская научная студенческая конференция молодых ученых “Наука. Технологии. Инновации” (Новосибирск, 2012). Тезисы опубликованы.
3. Научная студенческая конференция “Дни науки НГТУ” (Новосибирск, 2013). Присужден диплом I степени. Тезисы опубликованы.
4. 51-ая международная научная студенческая конференция “Студент и научно-технический прогресс” (Новосибирск, 2013). Присужден диплом I степени. Тезисы опубликованы.
5. Новосибирская межвузовская научная студенческая конференция “Студент и научно-технический прогресс” (Новосибирск, 2013). Присужден диплом II степени. Тезисы опубликованы.
6. XIV Всероссийская конференция молодых ученых по математическому моделированию и информационным технологиям (Томск, 2013). Тезисы опубликованы.
7. Всероссийская научная студенческая конференция молодых ученых “Наука. Технологии. Инновации” (Новосибирск, 2013). Присужден диплом I степени. Тезисы опубликованы.
8. Конференции молодых ученых и студентов «Актуальные проблемы геологии нефти и газа Сибири», посвященная 80-летию академика А.Э. Конторовича. (Новосибирск, 2014). Тезисы опубликованы.
9. Российская научно-техническая конференция «Инновации и научно-техническое творчество молодежи» (Новосибирск, 2014). Тезисы опубликованы.
10. Научная студенческая стендовая конференция “Дни науки НГТУ” (Новосибирск, 2014).
11. 52-ая международная научная студенческая конференция “Студент и научно-технический прогресс” (Новосибирск, 2014). Тезисы опубликованы.
Работа выполнена при поддержке интеграционного проекта №98 СО РАН.
Математическая модель
Широкий диапазон научных и инженерных задач предполагает многомасштабность (например, среды с мелкими включениями). Традиционные подходы, как известно, применимы для ограниченных пространственных и временных масштабов.
Прямое численное решение в условиях многомасштабности остается трудоемким даже с появлением суперкомпьютеров. Основной проблемой прямого решения является большой объем вычислений. Требуется много процессорного времени. Ситуация может быть несколько улучшена с использованием параллельных вычислительных технологий, однако это не снизит размеры дискретной задачи. При этом прямые методы обеспечивают получение информации о физических процессах на всех масштабах. Но в конкретных задачах часто бывает достаточно предсказать макроскопические свойства многомасштабной системы. Таким образом нужен метод, который улавливает мелкие влияния на больших масштабах, но не требует разрешения всех мелких особенностей.
Активное развитие многомасштабных методов началось с середины 1990-х годов после выхода работы [16]. Многомасштабные методы численного моделирования являются молодой отраслью вычислительной математики, поэтому исследования в этой области очень актуальны. Многие статьи по данной тематике или носят теоретический характер [3, 8, 16] или посвящены решению модельных задач [1, 15, 18]. Среди приложений можно выделить задачи течения жидкости в пористых средах [4, 11], определения электромагнитных [2], тепловых [6, 12, 30], упругих [26] характеристик композитных материалов, молекулярной динамики [9], гомогенизации кристаллов [13].
Многомасштабные задачи могут быть разделены на два класса:
· определение эффективных характеристик среды [10, 15, 23, 30] (решение обратной задачи),
· решение задачи с микровключениями [14] (оценка решения, учитывающего микроособености задачи).
В настоящее время при исследовании физических свойств гетерогенных сред используются гетерогенные многомасштабные методы [20,21,24] и многомасштабные конечноэлементные методы [1,7,9,10,15,29], построенные на декомпозиции пространства решений на сумму двух подпространств: «грубого», отвечающего за эффективные свойства среды, и «мелкого», позволяющего достаточно точно учесть свойства включений.
Гетерогенной средой (или системой) называется макроскопическая неоднородная система, состоящая из однородных компонент, разграниченных поверхностями раздела [22]. Все многообразие композитных материалов можно разбить на несколько групп:
· структура с вкраплениями (рисунок 1.а) состоит из связующего материала 1, в котором хаотически или упорядоченно распределены неконтактирующие между собой включения одной или нескольких компонент 2;
· структура с взаимопроникающими компонентами (например, нефте-, водо- и газоносные грунты, волокнистые материалы и тд.) (рисунок 1.б)

Рисунок 1 – Гетерогенные среды с различной структурой: а – структура с вкраплениями; б – структура с взаимопроникающими компонентами; в, г – комбинированные структуры с взаимопроникающими компонентами и краплениями; д – структура зернистого материала в состоянии свободной засыпки
Структуры, изображенные на рисунке 1, принято называть хаотическими [22]. Такой вид характерен для большинства естественных материалов (например, горные породы). Неупорядоченные структуры довольно сложно исследовать. Если построить упорядоченную систему, которая при этом сохранит основные черты хаотической (например, объемное соотношение компонент), то при исследованиях можно последнюю заметить адекватной ей упорядоченной структурой [20, 22].
Эффективные характеристики систем с упорядоченной и хаотической структурой равны друг другу, если эти структуры адекватны, а свойства компонент и их объемные концентрации одинаковы [22].
Все объекты моделирования можно разделить на две группы:
· естественные материалы (например, горные породы),
· искусственные материалы.
Естественные материалы, как правило, обладают сложной структурой (например, хаотической), которая заранее не известна. Поэтому на начальном этапе переходят к исследованиям искусственных материалов, свойства и структура которых уже известна. Чаще всего в качестве таких искусственных материалов выбирается упорядоченная, периодическая структура [30, 33].
В данной работе качестве гетерогенной среды будем рассматривать искусственный материал, состоящий из основной среды и мелкомасштабных включений разной геометрии с контрастными электрическими свойствами.
Уравнения Максвелла
В теории электромагнитного поля взаимодействие между зарядами описывается уравнениями Максвелла: системой связанных дифференциальных уравнений в частных производных. В большинстве работ по электромагнетизму уравнения записывают в следующем виде [5, 15]:
Закон Фарадея:
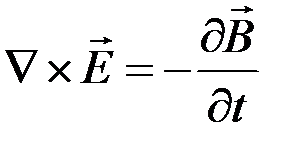
Закон Ампера:
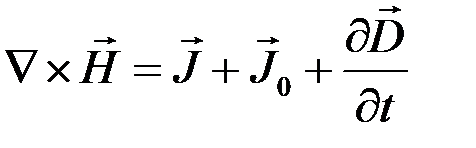
Уравнение Пуассона:

Магнитная индукция соленоида:
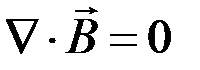
где 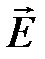 - напряженность электрического поля,
- напряженность электрического поля, 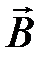 - магнитная индукция,
- магнитная индукция,  - напряженность магнитного поля,
- напряженность магнитного поля,  - электрическая индукция,
- электрическая индукция, 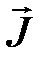 - плотность тока,
- плотность тока,  - плотность сторонних токов (возбуждающих электрическое поле),
- плотность сторонних токов (возбуждающих электрическое поле),  - плотность электрических зарядов,
- плотность электрических зарядов,
Запишем соотношения, связывающие величины  ,
, 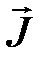 с
с 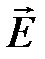 ,
,  с
с 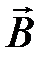 и учитывающие индивидуальные свойства среды:
и учитывающие индивидуальные свойства среды:
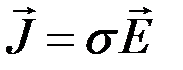
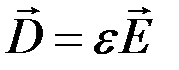
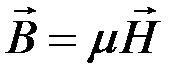
где 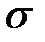 - электропроводность,
- электропроводность,  - диэлектрическая проницаемость,
- диэлектрическая проницаемость, 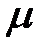 - магнитная проницаемость.
- магнитная проницаемость.
Перепишем систему - с учетом материальных уравнений -:



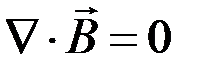
Далее в работе будет рассматриваться только стационарная задача.
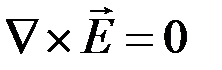
В этом случае вектор-функцию 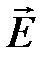 можно искать в виде градиента скалярной функции
можно искать в виде градиента скалярной функции 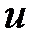 (электрический потенциал):
(электрический потенциал):
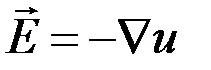
Тогда с учетом представления получаем:
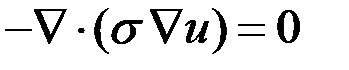
Таким образом, математической моделью рассматриваемого процесса является однородное уравнение эллиптического типа с краевыми условиями первого и второго рода.
Постановка задачи
Область моделирования, рисунок 3. При этом размеры и количество включений могут меняться.
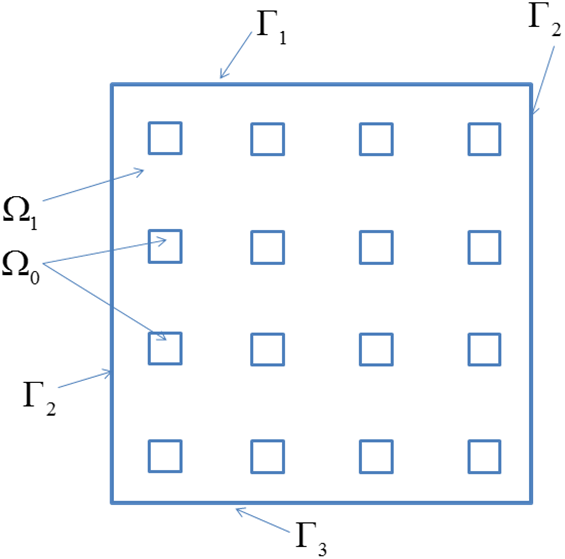
Рисунок 3 – Область моделирования
Решается однородное эллиптическое уравнение в  .
.
Полагаем, что на границах 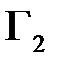 заданы однородные вторые краевые условия; на границах
заданы однородные вторые краевые условия; на границах  заданы значения потенциалов, т.е. первые краевые условия:
заданы значения потенциалов, т.е. первые краевые условия:
 ,
,
 ,
,
 ,
,
где 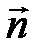 - единичная внешняя нормаль.
- единичная внешняя нормаль.
Вариационная постановка
Введем следующие гильбертовы пространства:

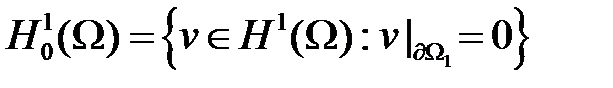
Абстрактная вариационная постановка выглядит следующим образом.
Определить 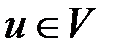 такую, что
такую, что
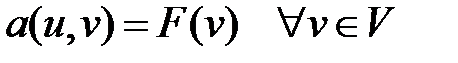 ,
,
где 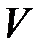 - гильбертово пространство,
- гильбертово пространство, 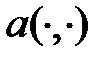 - непрерывная, коэрцитивная билинейная форма на пространстве
- непрерывная, коэрцитивная билинейная форма на пространстве 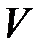 ,
, 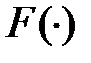 - непрерывная линейная форма на
- непрерывная линейная форма на 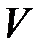 .
.
Тогда для эллиптической краевой задачи с краевыми условиями - вариационная постановка примет вид:
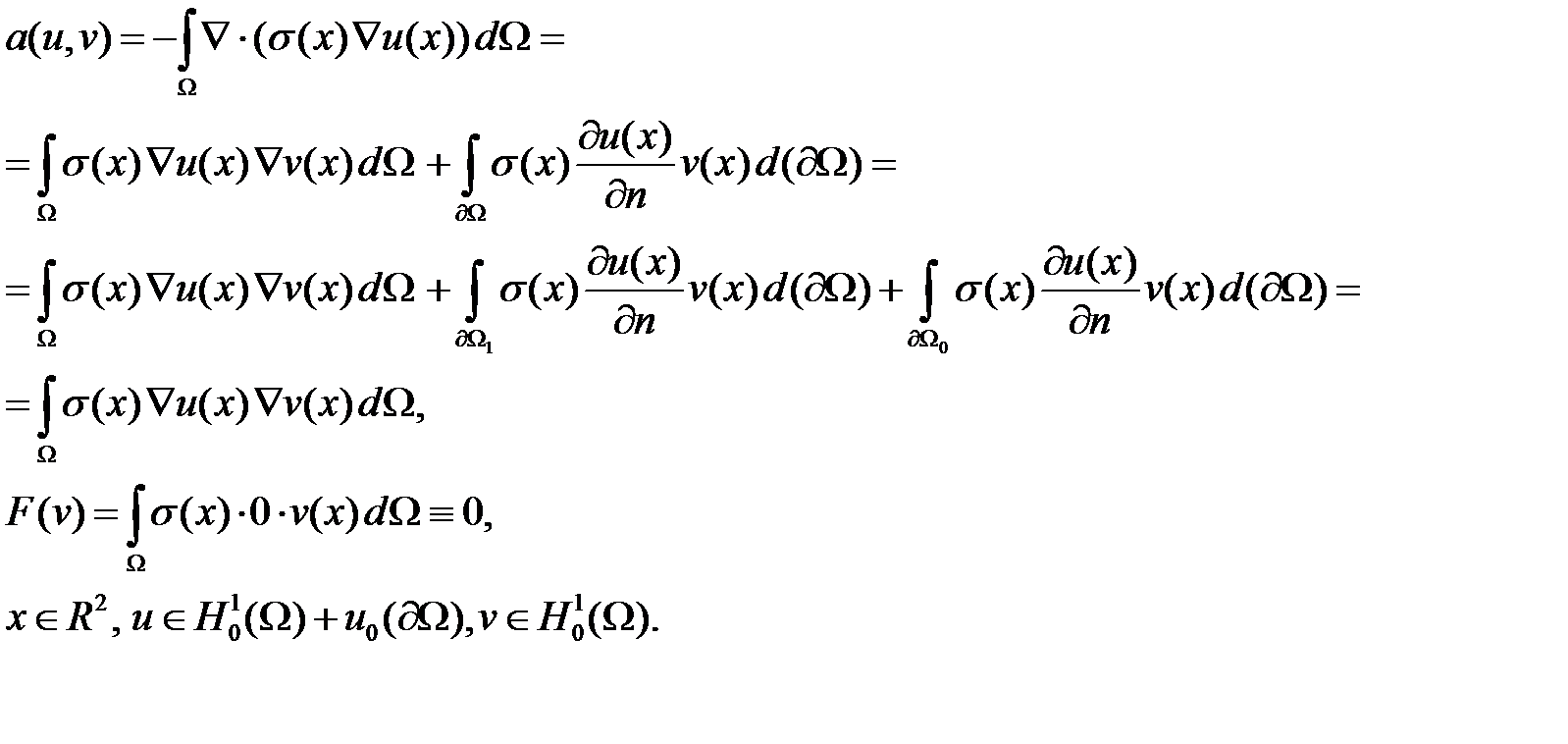
То есть:
Найти 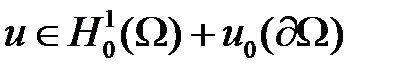 такую, что
такую, что  выполняется
выполняется
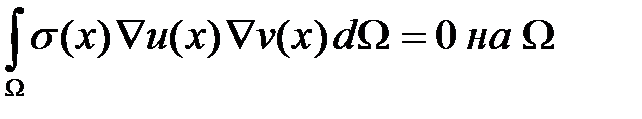
Вывод решения.
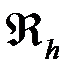
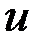 Решив систему, получаем вектор , компоненты которого являются значениями скалярного потенциала в узлах грубой сетки . Однако чаще всего необходимо знать решение не только в узлах сетки, но и в каждой точке области моделирования.
Решив систему, получаем вектор , компоненты которого являются значениями скалярного потенциала в узлах грубой сетки . Однако чаще всего необходимо знать решение не только в узлах сетки, но и в каждой точке области моделирования.
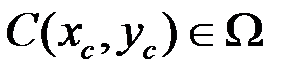 Для того чтобы определить значение скалярного потенциала в точке апрапрапаапра, можно воспользоваться следующим алгоритмом:
Для того чтобы определить значение скалярного потенциала в точке апрапрапаапра, можно воспользоваться следующим алгоритмом:
1. 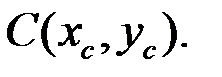
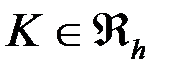 Определить к какому элементу принадлежит точка
Определить к какому элементу принадлежит точка
2. 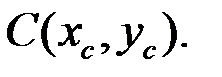
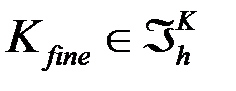 Определить к какому элементу принадлежит точка
Определить к какому элементу принадлежит точка
3. 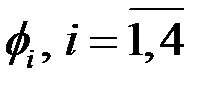 Для каждой многомасштабной функции найти:
Для каждой многомасштабной функции найти: 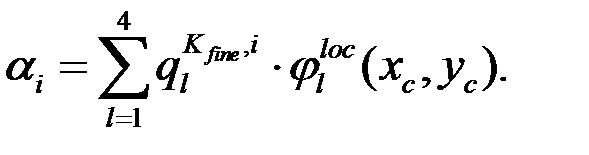
4. Вычислить значение потенциала по формуле: 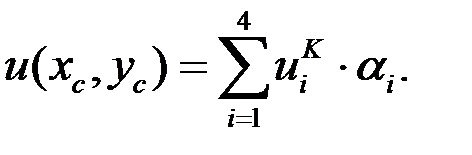
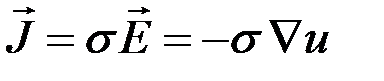 Еще бывает необходимо знать значения векторных величин, например, плотности тока: . Найдем плотность тока в точке
Еще бывает необходимо знать значения векторных величин, например, плотности тока: . Найдем плотность тока в точке 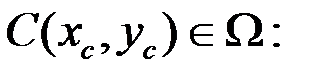
1. 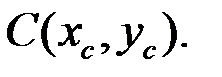
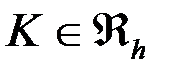 Определить к какому элементу принадлежит точка
Определить к какому элементу принадлежит точка
2. 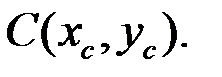
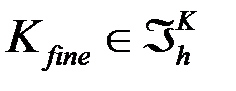 Определить к какому элементу принадлежит точка
Определить к какому элементу принадлежит точка
3. 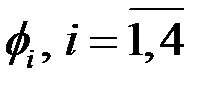 Для каждой многомасштабной функции найти:
Для каждой многомасштабной функции найти: 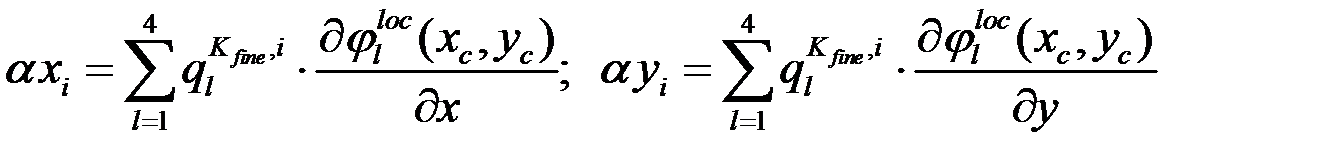
4. 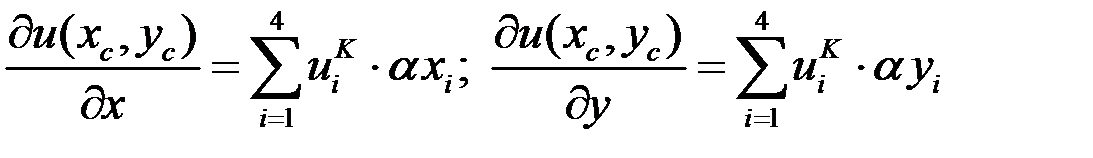
5. Отсюда получаем плотность тока:
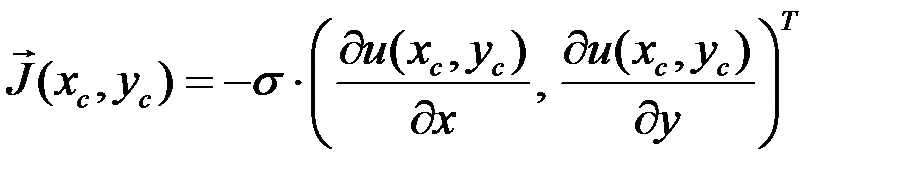
Эффективное сопротивление.
При исследовании гетерогенных сред было обнаружено, что в объемах превышающих объем одного включения проявляются устойчивые физические характеристики (например, теплопроводность электропроводность), в общем случае отличающимися от характеристик отдельных компонент. Такие характеристики среды называют эффективными [23,10,15].
Определение эффективного удельного электрического сопротивления гетерогенной среды осуществляется следующим образом [33]:
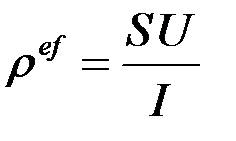 ,
,
где S – площадь сечения, перпендикулярного течению тока исследуемого образца, U – разность потенциалов, I – полный ток в образце, определяемый по формуле
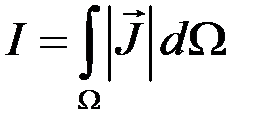
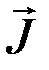
где – плотность тока.
Верификация
Верификацию программного комплекса будем производить в области с небольшим количеством включений.
Сформулируем задачу:
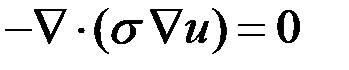
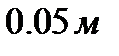 В качестве расчетной области возьмем прямоугольную область
В качестве расчетной области возьмем прямоугольную область 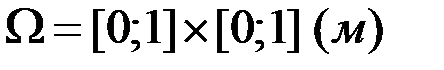 вапрапрапрапренгап(рисунок 9).
вапрапрапрапренгап(рисунок 9).

Рисунок 9 – Область моделирования  с грубой сеткой
с грубой сеткой
На границах заданы краевые условия (рисунок 3):
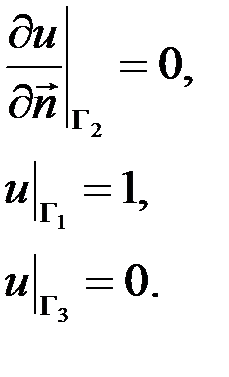
Электропроводность определяется следующим образом:
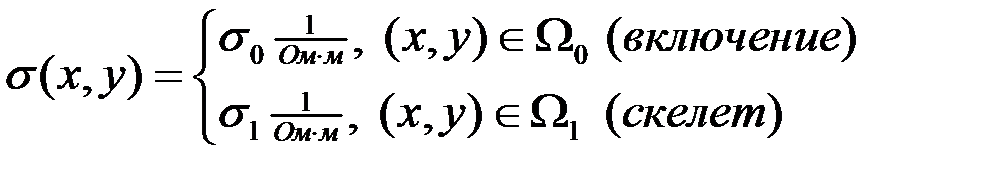
СЛАУ решается с фиксированной точность 10-8.
Относительную погрешность будем оценивать по формуле:
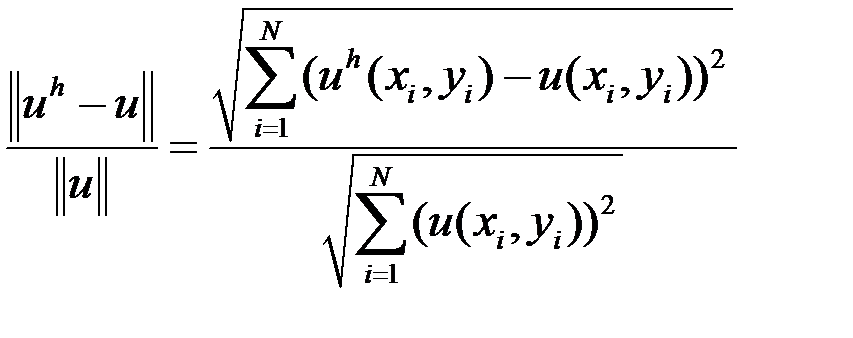 ,
,
где 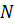 – количество рассматриваемых точек,
– количество рассматриваемых точек, 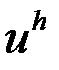 – полученное решение,
– полученное решение, 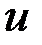 – точное решение.
– точное решение.
Пусть 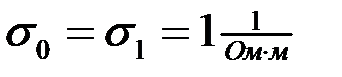 , тогда задача с краевыми условиями имеет аналитическое решение
, тогда задача с краевыми условиями имеет аналитическое решение
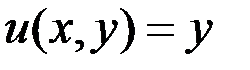
В таблице 1 приведены относительные погрешности решения, полученного МКЭ [28] и многомасштабным МКЭ.
Таблица 1 – Сравнение полученных решений и точного решения
|
| 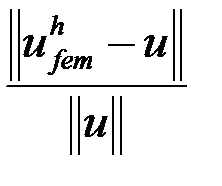
| 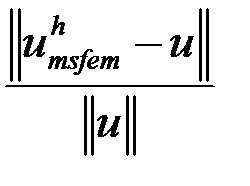
|
| По прямой 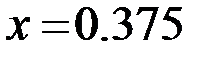 при при 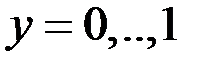
| 1.4200E-08
| 1.0443E-08
|
Если 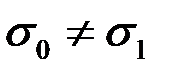 , то задача с краевыми условиями не имеет аналитического решения и результаты, полученные многомасштабным МКЭ будем сравнивать с результатами классического МКЭ на подробной сетке. Пусть
, то задача с краевыми условиями не имеет аналитического решения и результаты, полученные многомасштабным МКЭ будем сравнивать с результатами классического МКЭ на подробной сетке. Пусть 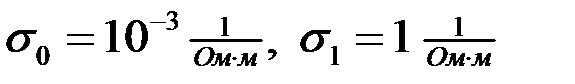 , т.е. включения непроводящие. Результаты моделирования приведены на рисунке 10 и в таблице 2
, т.е. включения непроводящие. Результаты моделирования приведены на рисунке 10 и в таблице 2
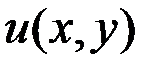
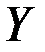
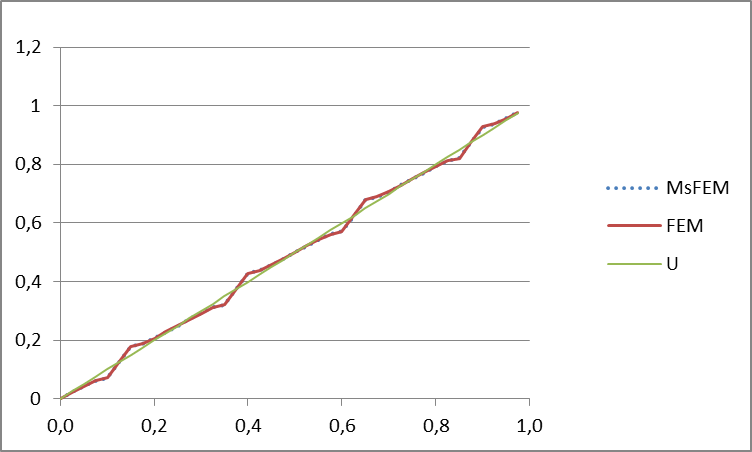
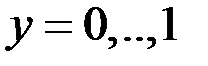
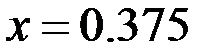 Рисунок 10 – Значения скалярного потенциала на прямой при арварарр(проходит через центры включений)
Рисунок 10 – Значения скалярного потенциала на прямой при арварарр(проходит через центры включений)
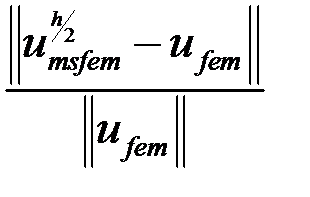
Таблица 2 – Числовые характеристики решения на вложенных сетках
|
| 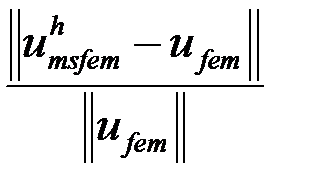
| 
|
| В узлах грубой сетки
| 2.51E-08
| 1.72E-08
|
| На прямой x=0.375
| 8.51E-04
| 2.61E-04
|
| На прямой y=0.375
| 4.98E-04
| 5.05E-04
|
На рисунке 11 изображено распределение скалярного потенциала. На рисунке 12 - векторное поле плотности тока.
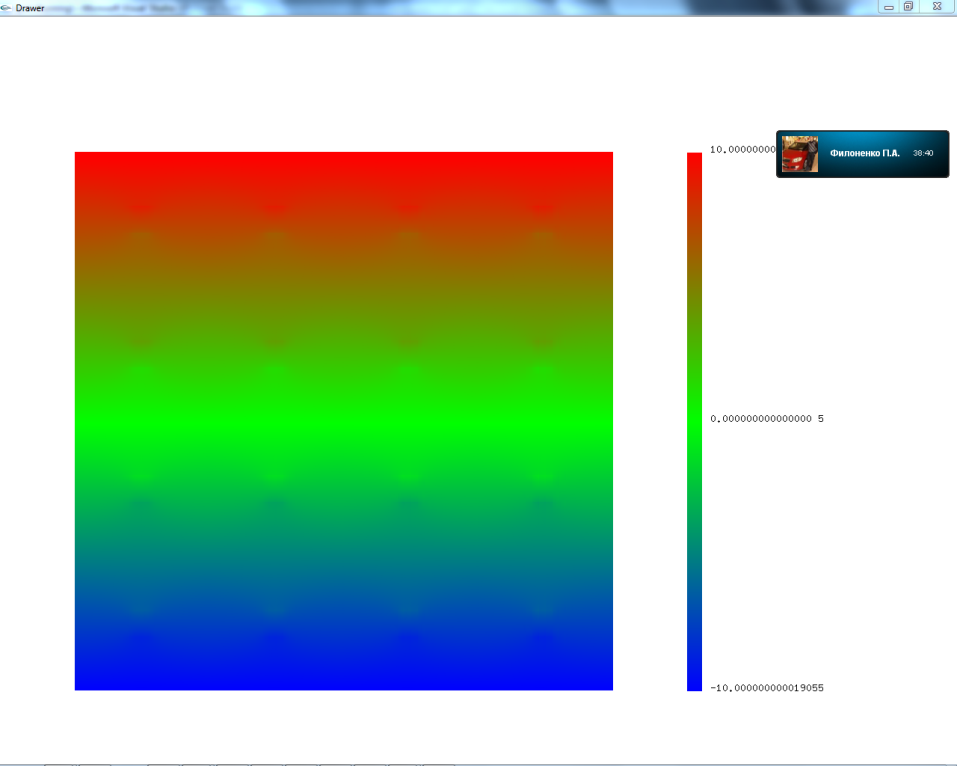

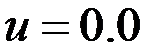

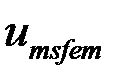
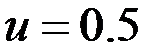

Рисунок 11– Распределение скалярного потенциала апрапр

Рисунок 12 – Векторное поле плотности тока


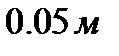
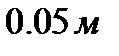
 Рассмотрим задачу - в области
Рассмотрим задачу - в области 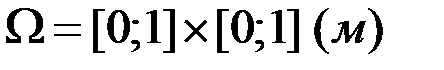 (рисунок 13)
(рисунок 13)
 Рисунок 13 – Область моделирования с грубой сеткой
Рисунок 13 – Область моделирования с грубой сеткой
В данной области включения пересекают границы грубых элементов, поэтому необходимо использовать осциллирующие краевые условия. Вид базисной функции для данной области на рисунке 6. Причем в тех макроэлементах, где нет включений, можно многомасштабные базисные функции не строить.
Результаты моделирования приведены на рисунках 14 и 15.

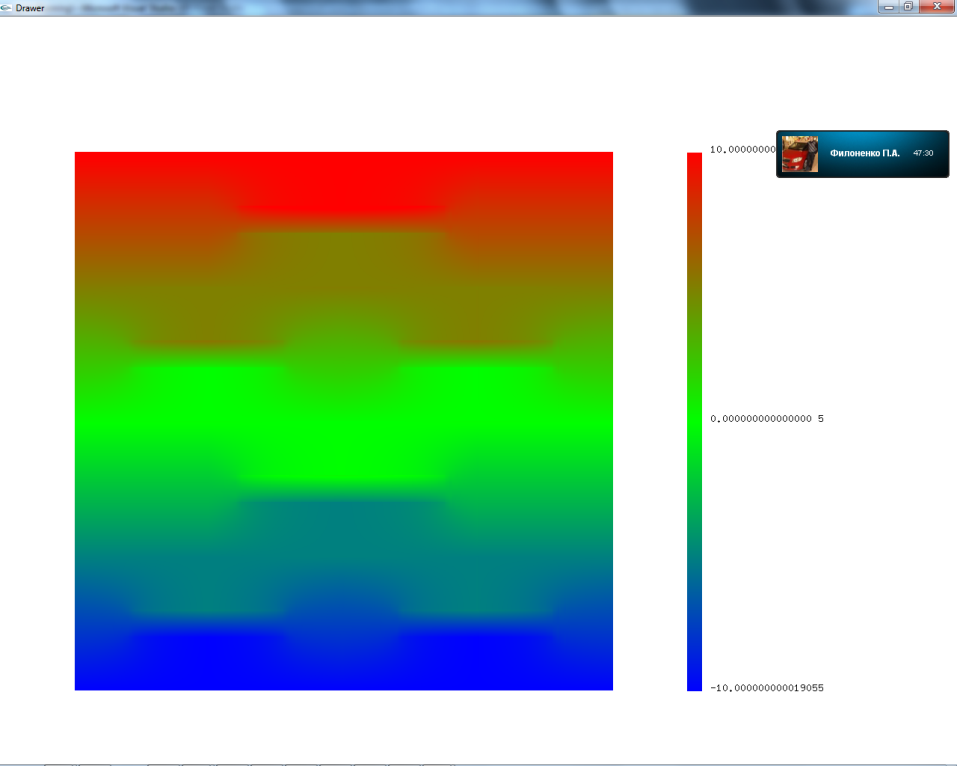


Рисунок 14 – Распределение скалярного потенциала

Рисунок 15 – Векторное поле плотности тока
Результаты моделирования
Экономический расчёт
Что-то тут пишем
Заключение
В работе было рассмотрено решение двумерной эллиптической краевой задачи с контрастными коэффициентами многомасштабным методом конечных элементов. Для решения задачи был реализован алгоритм многомасштабного метода конечных элементов [10]. Для проверки результатов задача так же решалась с помощью классического метода конечных элементов [28]. Найденное обоими методами распределение скалярного потенциала практически совпадают (с точностью до 10-5). Однако многомасштабный метод позволяет решать задачи с более мелкими включениями за счет независимого построения сетки в каждом макроэлементе. Это так же позволяет эффективно распараллеливать метод (получено почти линейное ускорение).
Реализованный алгоритм не предполагает периодичности решения или мелкомасштабных включений и может быть использован при моделировании как геометрически неоднородных, так и разномасштабных включений. Для удобства анализа результатов моделирования был реализован визуализатор, позволяющий по полученному решению получить вид распределения скалярного потенциала (рисунки 11, 12) и векторного поля плотности тока (рисунки 12, 15).
Работа была представлена на студенческой научной конференции ФПМИ, где получила второе место, и на новосибирской межвузовской студенческой конференции «Интелектуальный потенциал Сибири», а так же была опубликована [34].
Список литературы
1. Allaire, G. A multiscale finite element method for numerical homogenization / G. Allaire, R. Brizzi // SIAM MMS. – 2005. – 4. – С. 790-812.
2. Banks, H.T. Homogenization of Periodically Varying Coefficients in Electromagnetic Materials / H.T. Banks [и др.] // SAMSI: Technical Report. – 2005. – N2005-2. – С. 1-20.
3. Bensoussan, A. Asymptotic analysis for periodic structures / A. Bensoussan, J.L. Lions, G. Paranicolaou. – Noth-Holland: New York, 1978. – 721 с.
4. Bochev, P. A Mathematical Framework for Multiscale Science and Engineering: The Variational Multiscale Method and Interscale Transfer Operators / P. Bochev [и др.] // SAND REPORT. – 2004. – 2004-2871. – С. 1-20.
5. Bondeson, A. Computational Electromagnetics / A. Bondeson, T. Rylander, P. Ingelström. – B.: Springer, 2000. – 231 с.
6. Durmaz, S. A numerical study on the effective thermal conductivity of composite materials / S. Durmaz. – IZMIR, 2004. – 240 с.
7. E, W. Multiscale modeling and computation / W. E, B. Engquist // Notices Amer. Math. Soc.. – 2003. – V. 50: № 9. – С. 1062-1070.
8. E, W. Analysis of the heterogeneous multiscale method for ellpiptic homogenization problems / W. E, P. Ming, P. Zhang // J. Am. Math. Soc.. – 2003. – vol. 18. – С. 121-156.
9. E, W. The heterogeneous multiscale methods / W. E, B. Engquist // Comm. Math. Sci. – 2003. – vol. 1, no. 1. – С. 87-132.
10. Efendiev Y. Multiscale Finite Element Methods: Theory and Applications / Efendiev Y., Hou T. Y. – B.: Springer, 2009. – 241 с.
11. Efendiev, Y. Accurate multiscale finite element methods for two-phase flow simulations / Y. Efendiev, V. Ginting, T. Hou // Journal of Computational Physics. – 2006. – vol. 220, no.1. – С. 155-174.
12. Gilbert, A.C. A Comparison of Multiresolution and Classical One-dimensional Homogenoztion Schemes / A.C. Gilbert // Applied and Computational Hamonic Analysis. – 1998. – vol. 5, no. 1. – С. 1-35.
13. Guenneau, S. Homogenization of 3D finite chiral photonic crystals / S. Guenneau, F. Zolla // Phisica B. – 2007. – vol. 394. – С. 145-147.
14. Jiang, P.-X. Experimental research on convection heat transfer in sintered porous plate channels / Pei-Xue Jiang // International Journal of Heat and Mass Transfer. – 2004. – №47. – С. 2086-2096.
15. Hou. T. Y. A Multiscale Finite Element Method for Elliptic Problems in Composite Materials and Porous Media / Hou. T. Y., X.-H. Wu // Journal of computational physics. – 1997. – 134. – С. 169-189.
16. Hou, T. Convergence of a multiscale finite element method for elliptic problems with rapidly oscillating coefficients / T. Hou, X.-H. Wu, Z. Cai // Mathematics of Computation. – 1999. – vol. 68: no. 227. – С. 913-943.
17. Saad, Y. Iterative Methods for Sparse Linear Systems / Y. Saad. – 2nd edition. – B.: SIAM Society for Industrial & Applied Mathematics, 2003. – 477 с.
18. Sangalli, G. Capturing small scales in elliptic problems using a residual-free bubbles finite element method [Электронный ресурс] / G. Sangalli. – Режим доступа: http://www.siam.org/journals/mms/x-x/41140.html.
19. Weinan, E. Principles of Multiscale Modeling / E. Weinan. – New Jersey: Princeton University, 2011. – 488 с.
20. Бахвалов, Н.С. Осреднение процессов в периодических средах. / Н.С. Бахвалов, Г.П. Панасенко. – М.: Наука, 1984. – 352 с.
21. Бахвалов, Н.С. Осреднение дифференциальных уравнений с частными производными с быстро осциллирующими коэффициентами. / Н.С. Бахвалов // ДАН. – 1975. – Т.221: №3. – С. 516-519.
22. Дульнев, Г.Н. Теплопроводность смесей и композитных материалов: Справочная книга / Г.Н. Дульнев, Ю.П. Заричняк. – Л.: Энергия, 1974. – 264 с.
23. Жиков, В.В. Усреднение дифференциальных операторов / В.В. Жиков, С.М. Козлов, О.А. Олейник. – М.: Физматлит, 1993. – 464 с.
24. Жиков, В.В. Усреднение и перколяция / В.В. Жиков, С.М. Козлов // УМН. – 1988. – Т.43: №4. – С. 169-170.
25. Иткина, Н.Б. Использования многомасштабного метода для моделирования процесса диффузии гетерогенных средах / Н.Б. Иткина, Э.П. Шурина, Ю.И. Шокин. – Новосибирск: Изд-во НГТУ, 2009. – 10 с.
26. Копысов, С.П. Об одном методе определения эффективных характеристик композитов с помощью вейвлет-преобразования / С.П. Копысов, Ю.А. Сагдеева // Интеллектуальные системы в производстве. – 2007. – номер 1. – С. 49-62.
27. Ольшанский, М.А. Лекции и упражнения по многосеточным методам / М.А. Ольшанский. – М.: Физматлит, 2005. – 168 с.
28. Соловейчик, Ю.Г. Метод конечных элементов для решения скалярных и векторных задач: учеб. пособие / Ю.Г. Соловейчик, М.Э. Рояк, М.Г. Персова. – Новосибирск: Изд-во НГТУ, 2007. – 896 с.
29. Федоренко, Р.П. Введение в вычислительную физику / Р.П. Федоренко. – М.: Изд-во МФТИ, 1994. – 528 с.
30. Чишкала, В.А. Теплопроводность композиционных материалов на основе гидрида алюминия и терморасширенного графита. / В.А. Чишкала [и др.] // Вестник Харьковского университета. – 2008. – № 794. – С. 81-84.
31. Шокин, Ю.И. Многомасштабные методы: учеб. пособие / Ю.И. Шокин, Э.П. Шурина, Н.Б. Иткина. – Новосибирск: Изд-во НГТУ, 2010. – 68 с. – (Современные многосеточные методы; Часть I).
32. Шурина, Э.П. Методы решения СЛАУ большой рзмерности / Э.П. Шурина, М.Ю. Баландин. – Новосибирск: Изд-во НГТУ, 2000. – 70 с.
33. Эпов, М.И. Численная гомогенизация электрических характеристик сред с контрастными мелкомасштабными включениями / М.И. Эпов, Э.П. Шурина, М.К. Артемьев // Доклады академии наук. – 2011. – том 442: №1. – С. 1-3.
34. Кутищева, А.Ю. Решение эллиптической краевой задачи с контрастными коэффициентами многомасштабным методом конечных элементов: тезисы доклада / А.Ю. Кутищева // Современные проблемы технических наук. – 2012. – Часть 1. – С. 11.
Приложение А. ММКЭ
class MultiscaleFiniteElementMethods
{
private:
char direct[50];
std::vector<int> _use; //нужна для предотващени записи в один участок памяти
int TEST;
void input(double sig);
double func(double x, double y, int EL, int el);
double gauss (double a, double b, double c, double d, int EL, int el);
void enter_kraev4(int number, int El, int bf, double value, RarefiedMatrix A_fine[]);
void MFE_fine_elem(int current_elem, RarefiedMatrix A_fine[]);
double mult(std::vector<double>&x, std::vector<double>&y);
void local_matrix(int elem, int El, double koef[4][4], double G_loc[4][4], double b_loc[4]);
void MMFE_local_matrix(int elem, RarefiedMatrix A_fine[], int size);
void MMFE();
protected:
std::vector <grid> all_grids; //хранит все сетки. Первый элемент: coarse-grid. Остальные fine-grid в порядке их глобальной нумерации
std::vector <EnterTheBoundaryConditions> all_edges; //все краевые
int G_1[2][2], M_1[2][2]; //матрицы одномерных элементов
/*блок функций, отвечающих за генерацию портрета матрицы*/
struct spisok //для формировании портрета матрицы
{
int elem;
spisok *next;
};
void add(int min, int max, spisok *j);
void AssembiyPortrait(int el, RarefiedMatrix *Matrix, spisok *j);
void CreationPortrait(int el, RarefiedMatrix *Matrix);
void dimensional_matrix();
void global(int number_elem, int El, RarefiedMatrix *Matrix, double G_loc[4][4], double b_loc[4]);
void local_kraev3(int number, int El, RarefiedMatrix *Matrix);
void local_kraev2(int number, int El, RarefiedMatrix *Matrix);
void enter_kraev1(int number, int El, RarefiedMatrix *Matrix);
double X1(double x, double xmin, double xmax);
double X2(double x, double xmin, double xmax);
double Y1(double y, double ymin, double ymax);
double Y2(double y, double ymin, double ymax);
double dX(int i, double hx);
double dY(int i, double hy);
public:
bool _print;
bool _oscillating;
bool _parallel;
RarefiedMatrix A_coarse;//глобальная матрица coarse grid
double sigma[2];
MultiscaleFiniteElementMethods();
void PrintFullMatrix(char *file, int I, RarefiedMatrix A);
void PrintGl(char *file1, char *file2, RarefiedMatrix A, int I, int nX, int nY);
double PrintXY(double x, double y, std::vector<double> U, int El);
double PrintMsXY(double x, double y, std::vector<double> U);
std::vector <double> MultiscaleFiniteElementMethods::PrintJ(double x, double y, int El, int el);
double EffectiveResistance();




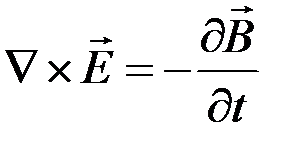
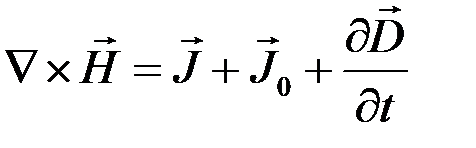

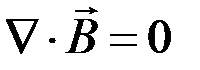
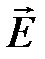 - напряженность электрического поля,
- напряженность электрического поля, 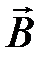 - магнитная индукция,
- магнитная индукция,  - напряженность магнитного поля,
- напряженность магнитного поля,  - электрическая индукция,
- электрическая индукция, 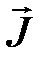 - плотность тока,
- плотность тока,  - плотность сторонних токов (возбуждающих электрическое поле),
- плотность сторонних токов (возбуждающих электрическое поле),  - плотность электрических зарядов,
- плотность электрических зарядов,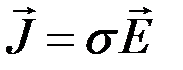
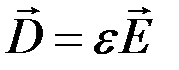
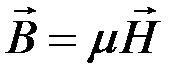
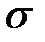 - электропроводность,
- электропроводность,  - диэлектрическая проницаемость,
- диэлектрическая проницаемость, 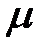 - магнитная проницаемость.
- магнитная проницаемость.


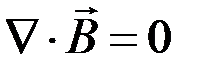
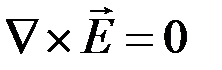
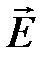 можно искать в виде градиента скалярной функции
можно искать в виде градиента скалярной функции 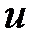 (электрический потенциал):
(электрический потенциал):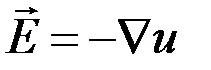
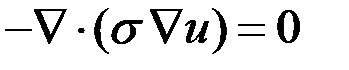

 .
.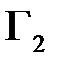 заданы однородные вторые краевые условия; на границах
заданы однородные вторые краевые условия; на границах  заданы значения потенциалов, т.е. первые краевые условия:
заданы значения потенциалов, т.е. первые краевые условия: ,
,  ,
,  ,
, 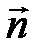 - единичная внешняя нормаль.
- единичная внешняя нормаль.
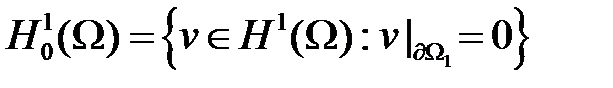
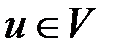 такую, что
такую, что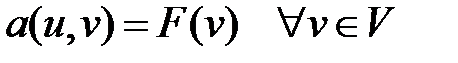 ,
, 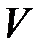 - гильбертово пространство,
- гильбертово пространство, 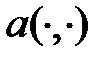 - непрерывная, коэрцитивная билинейная форма на пространстве
- непрерывная, коэрцитивная билинейная форма на пространстве 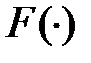 - непрерывная линейная форма на
- непрерывная линейная форма на 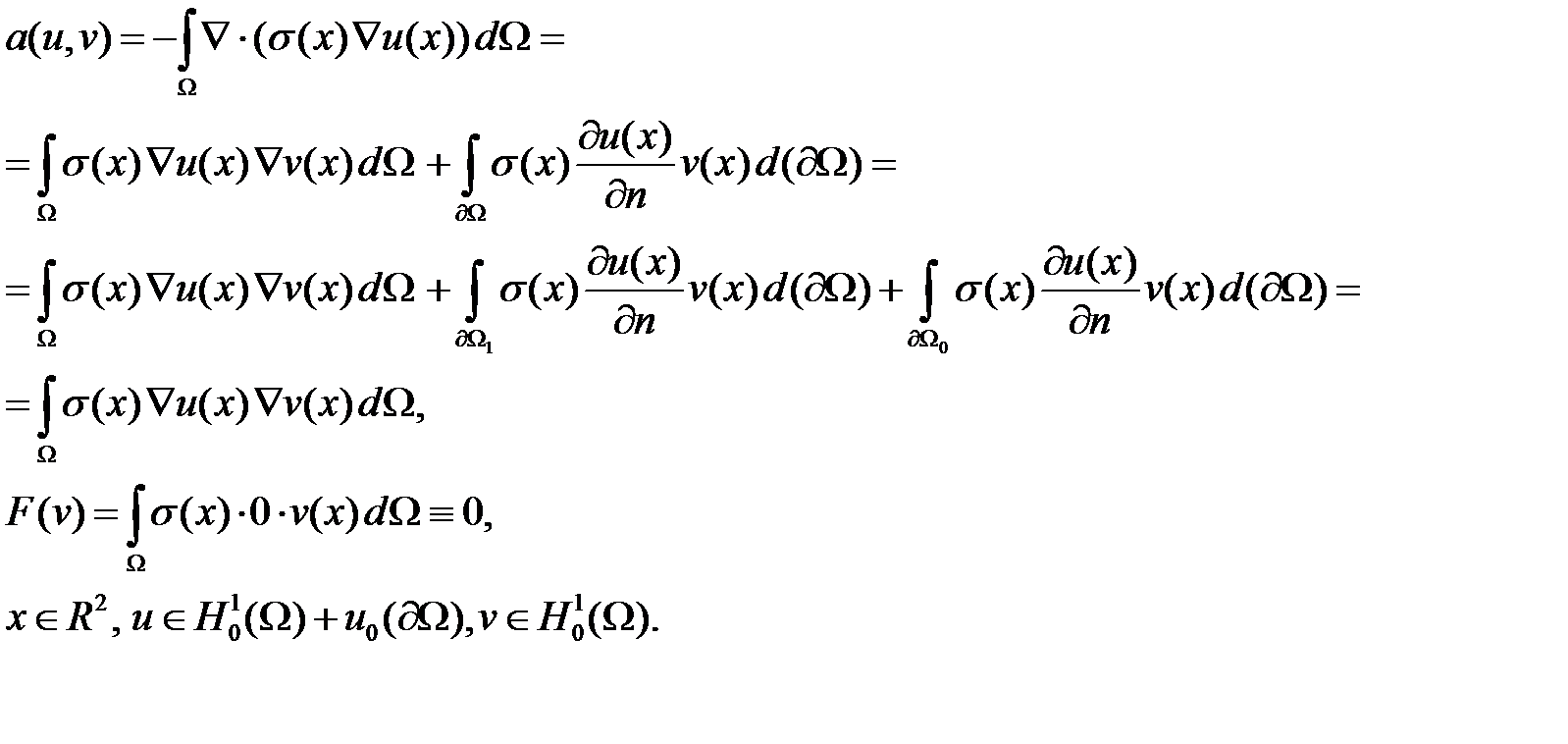
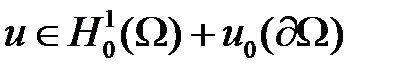 такую, что
такую, что  выполняется
выполняется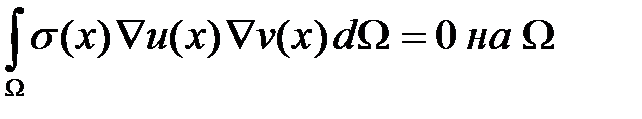
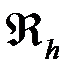
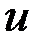 Решив систему, получаем вектор , компоненты которого являются значениями скалярного потенциала в узлах грубой сетки . Однако чаще всего необходимо знать решение не только в узлах сетки, но и в каждой точке области моделирования.
Решив систему, получаем вектор , компоненты которого являются значениями скалярного потенциала в узлах грубой сетки . Однако чаще всего необходимо знать решение не только в узлах сетки, но и в каждой точке области моделирования.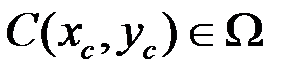 Для того чтобы определить значение скалярного потенциала в точке апрапрапаапра, можно воспользоваться следующим алгоритмом:
Для того чтобы определить значение скалярного потенциала в точке апрапрапаапра, можно воспользоваться следующим алгоритмом: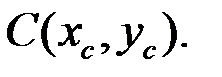
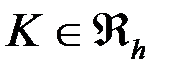 Определить к какому элементу принадлежит точка
Определить к какому элементу принадлежит точка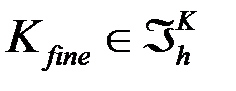 Определить к какому элементу принадлежит точка
Определить к какому элементу принадлежит точка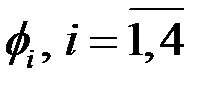 Для каждой многомасштабной функции найти:
Для каждой многомасштабной функции найти: 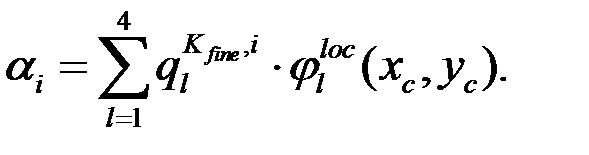
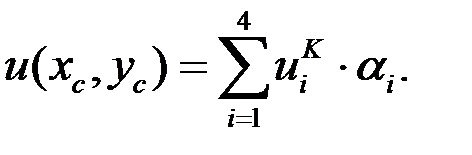
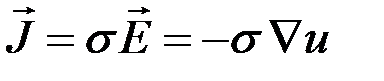 Еще бывает необходимо знать значения векторных величин, например, плотности тока: . Найдем плотность тока в точке
Еще бывает необходимо знать значения векторных величин, например, плотности тока: . Найдем плотность тока в точке 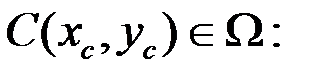
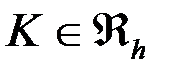 Определить к какому элементу принадлежит точка
Определить к какому элементу принадлежит точка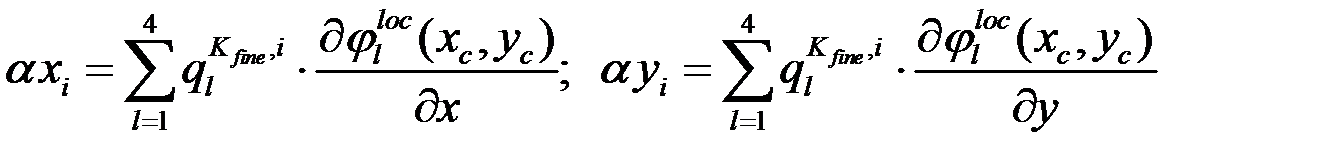
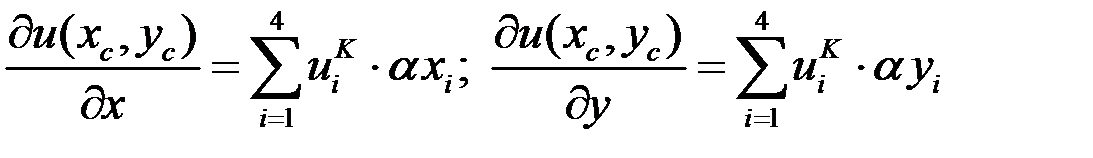
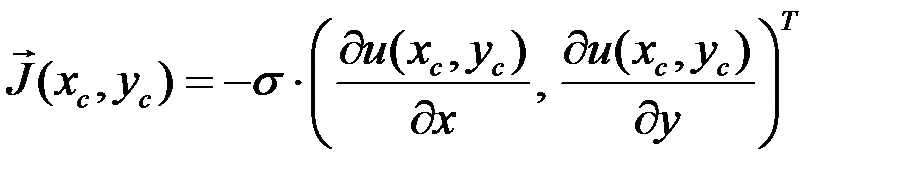
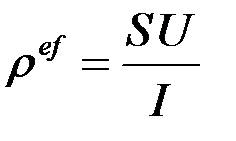 ,
, 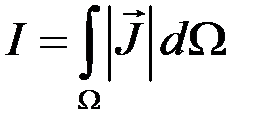
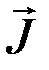
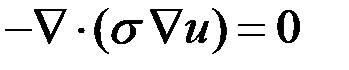
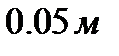 В качестве расчетной области возьмем прямоугольную область
В качестве расчетной области возьмем прямоугольную область 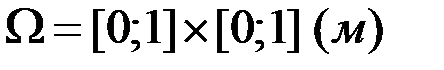 вапрапрапрапренгап(рисунок 9).
вапрапрапрапренгап(рисунок 9).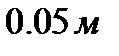

 с грубой сеткой
с грубой сеткой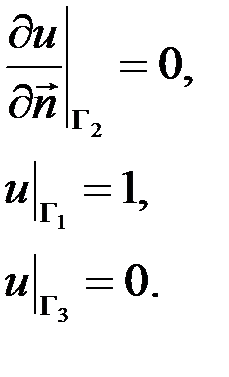
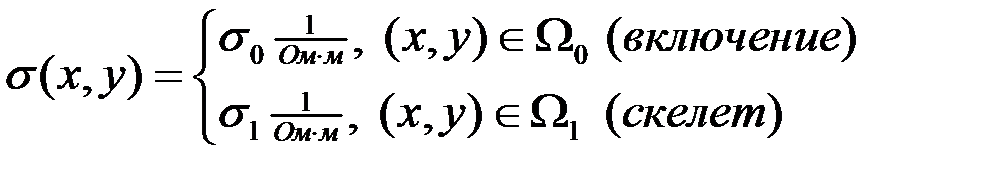
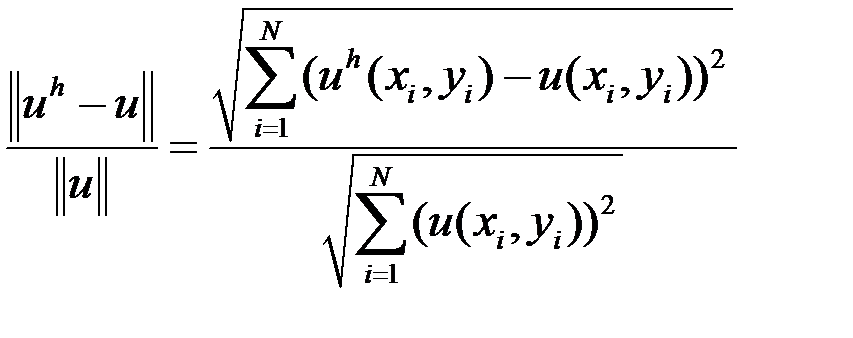 ,
, 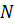 – количество рассматриваемых точек,
– количество рассматриваемых точек, 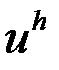 – полученное решение,
– полученное решение, 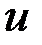 – точное решение.
– точное решение.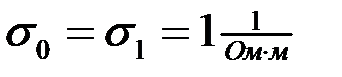 , тогда задача с краевыми условиями имеет аналитическое решение
, тогда задача с краевыми условиями имеет аналитическое решение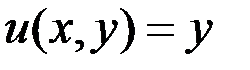
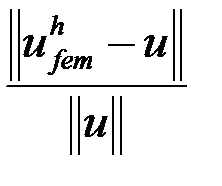
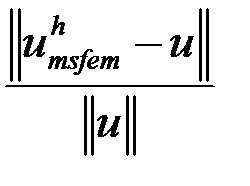
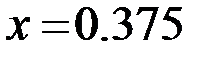 при
при 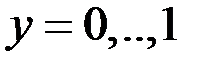
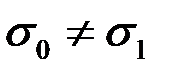 , то задача с краевыми условиями не имеет аналитического решения и результаты, полученные многомасштабным МКЭ будем сравнивать с результатами классического МКЭ на подробной сетке. Пусть
, то задача с краевыми условиями не имеет аналитического решения и результаты, полученные многомасштабным МКЭ будем сравнивать с результатами классического МКЭ на подробной сетке. Пусть 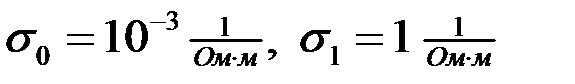 , т.е. включения непроводящие. Результаты моделирования приведены на рисунке 10 и в таблице 2
, т.е. включения непроводящие. Результаты моделирования приведены на рисунке 10 и в таблице 2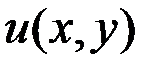
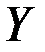

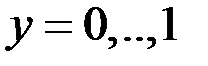
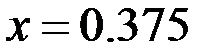 Рисунок 10 – Значения скалярного потенциала на прямой при арварарр(проходит через центры включений)
Рисунок 10 – Значения скалярного потенциала на прямой при арварарр(проходит через центры включений)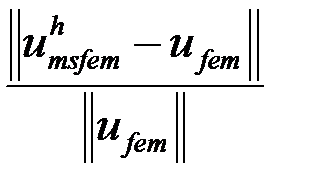



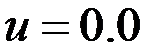

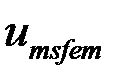
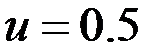



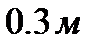 Рассмотрим задачу - в области
Рассмотрим задачу - в области 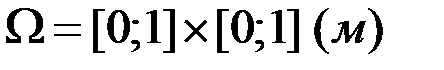 (рисунок 13)
(рисунок 13) Рисунок 13 – Область моделирования с грубой сеткой
Рисунок 13 – Область моделирования с грубой сеткой




