Рассмотрим на плоскости  , на которой введена прямоугольная декартова система координат
, на которой введена прямоугольная декартова система координат 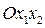 , общее уравнение кривой второго порядка:
, общее уравнение кривой второго порядка:
 , (1.14)
, (1.14)
где  - заданные действительные числа, для которых выполняется неравенство:
- заданные действительные числа, для которых выполняется неравенство:
 , (2.14)
, (2.14)
Из (1.14) и (2.14) следует, что уравнение (1.14) можно представить в виде
 , (3.14)
, (3.14)
где
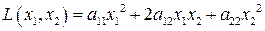 (4.14)
(4.14)
- квадратичная форма от переменных  .Из аналитической геометрии известно,что основными невырожденными кривыми второго порядка на плоскости
.Из аналитической геометрии известно,что основными невырожденными кривыми второго порядка на плоскости  являются эллипс, гипербола и парабола.
являются эллипс, гипербола и парабола.
Эллипс – этогеометрическое место точек на плоскости, сумма расстояний от которых до двух фиксированных точек плоскости  и
и 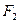 , называмых фокусами эллипса, есть величина постоянная, равная 2 a.
, называмых фокусами эллипса, есть величина постоянная, равная 2 a.
Если фокусы эллипса поместить в точках  и
и 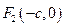 на координатной оси
на координатной оси 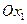 , то получим простейшее (каноническое) уравнение эллипса:
, то получим простейшее (каноническое) уравнение эллипса:
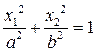 , (5.14)
, (5.14)
где большая и меньшая полуоси a и b эллипса связаны соотношением b 2 =
= a 2 - c 2 . При a = b уравнение (5.14) переходит в уранение окружности с центром в точке О и радиуса r = a.
Гипербола - множество точек на плоскости, абсолютная величина разности расстояний которых от двух фиксированных точек плоскости  и
и 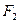 , называмых фокусами гиперболы, есть величина постоянная, равная 2 a.
, называмых фокусами гиперболы, есть величина постоянная, равная 2 a.
Если фокусы гиперболы поместить в точках  и
и 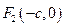 на координатной оси
на координатной оси 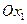 , то получим простейшее (каноническое) уравнение гиперболы:
, то получим простейшее (каноническое) уравнение гиперболы:
 (6.14)
(6.14)
где полуоси a и b гиперболы связаны соотношением b 2 = c 2 - a 2 .
Парабола - множество точек плоскость, равноудалённых от данной точки F (фокуса параболы) и данной прямой (директрисы).
Если фокус параболы поместить в точке  координатой оси
координатой оси 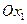 , где
, где
число p называется параметром параболы и по абсолютной величине равно расстоянию между фокусом и прямой 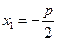 - директрисой параболы, то получим каноническое уравнение параболы:
- директрисой параболы, то получим каноническое уравнение параболы:
 (7.14)
(7.14)
Введём в рассморение величину
 , (8.14)
, (8.14)
которая является определителем матрицы 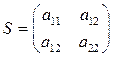 квадратичной формы
квадратичной формы
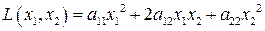 , входящей в общее уравнение (3.14) кривой второго порядка. Эта величина
, входящей в общее уравнение (3.14) кривой второго порядка. Эта величина 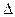 не меняется при преобразовании координат на плоскости, поэтому её называют инвариантом кривой второго порядка..
не меняется при преобразовании координат на плоскости, поэтому её называют инвариантом кривой второго порядка..
При линейном ортогональном преобразовании переменных на плоскости  , соотвествующем переходу от ортонормированного базиса
, соотвествующем переходу от ортонормированного базиса  к ортонормированному базису, состоящему из собственных векторов
к ортонормированному базису, состоящему из собственных векторов  матрицы S,
матрицы S,
совершается переход по формуле (9.13) от матрицы S к диагональной матрице
 , где
, где  - собственные числа матрицы S. Этот переход совершается с помощью ортогональной матрицы
- собственные числа матрицы S. Этот переход совершается с помощью ортогональной матрицы 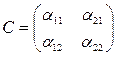 ,
,  , преобразования переменных:
, преобразования переменных: 
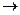
 . В результате этого квадратичная форма
. В результате этого квадратичная форма 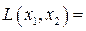 =
= 
 приводится к каноническому виду
приводится к каноническому виду 
 +
+ 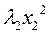 . При переходе от матрицы S к диагональной матрице B величина
. При переходе от матрицы S к диагональной матрице B величина 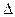 запишется в виде:
запишется в виде: 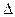 =
= 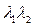 . На основании этого имеет место
. На основании этого имеет место
Теорема 1.14. Уравнение (1.14) всегда определяет либо окружность при  =
=  , либо эллипс при
, либо эллипс при 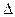 >0, либо гиперболу при
>0, либо гиперболу при 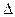 <0, либо параболу при
<0, либо параболу при
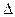 =0. При этом воможно вырождение для эллипса (окружности) в точку или мнимый эллипс, для гиперболы возможно вырождение в пару пересекающихся прямых, а для параболы - в пару параллельных прямых.
=0. При этом воможно вырождение для эллипса (окружности) в точку или мнимый эллипс, для гиперболы возможно вырождение в пару пересекающихся прямых, а для параболы - в пару параллельных прямых.
Эта теорема позволяет установить тип кривой второго порядка, не ипользуя переход к её каноническому виду. А само преобразование кривой второго порядка к каноническому виду производят по следующему общему правилу:1) находят то линейное преобазование координат, которое позволяет привести квадратичную форму 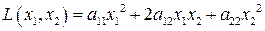 старших членов уравнения кривой к каноническому виду, и выполняют затем в уравнении кривой соответствующую замену переменных. В результате этого преобразования из уравнения кривой исчезают члены с произведениями координат;
старших членов уравнения кривой к каноническому виду, и выполняют затем в уравнении кривой соответствующую замену переменных. В результате этого преобразования из уравнения кривой исчезают члены с произведениями координат;
2) совершая после этого параллельный перенос новых осей координот  , приводят в итоге уравнение кривой к требуемому каноническому виду.
, приводят в итоге уравнение кривой к требуемому каноническому виду.
Пример1.14. Установить тип кривой и привести её уравнение

Решение. В данном случае, согласно формуле (8.14), 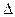 =5
=5  8 -
8 -  =36>0, т.е. это кривая эллиптического типа. Здесь матрица
=36>0, т.е. это кривая эллиптического типа. Здесь матрица  . Приведём её к диагональному виду. Для этого составим характеристическое уравнение этой матрицы:
. Приведём её к диагональному виду. Для этого составим характеристическое уравнение этой матрицы:
 , т.е.
, т.е.  .
.
Вычисляем её собственные числа  Для нахождения соответствующих им собственных векторов запишем ОСЛАУ:
Для нахождения соответствующих им собственных векторов запишем ОСЛАУ:
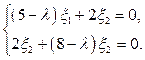
Полагая здесь  для определения соответствующего собственного вектора
для определения соответствующего собственного вектора  получаем систему уравнений
получаем систему уравнений
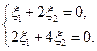
Отсюда  . Полагая
. Полагая  находим
находим  и
и  =
= 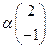 .Нормируя этот вектор, получим его орт-вектор
.Нормируя этот вектор, получим его орт-вектор  . Полагая
. Полагая 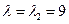 , получаем из ОСЛАУ для определения второго собственного вектора
, получаем из ОСЛАУ для определения второго собственного вектора  систему уравнений
систему уравнений

Отсюда имеем 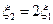 . Полагая
. Полагая 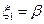 , находим
, находим  =
=  . Нормируя
. Нормируя  ,
,
получим его орт-вектор  .
.
Векторы 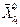 и
и  ортогональные, т.к. их скалярное произведение (
ортогональные, т.к. их скалярное произведение (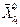

 )=0.
)=0.
Используем ортонормальные собственные векторы 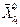 и
и  для построенияортогональной матрицы
для построенияортогональной матрицы 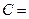 (
(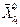 ,
,  ) преобразования координат:
) преобразования координат:

Отсюда получаем формулы ортогонального преобразования в координатной форме при переходе в Е2 к ортонормированному базису из собственных векторов матрицы S:
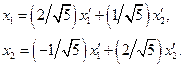
Найденные для  и
и  выражения, подставим в общее уравнение кривой:
выражения, подставим в общее уравнение кривой:
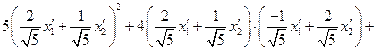
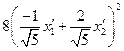 -
-
-32 
Откуда после раскрытия скобок и приведения подобных членов получим
4 
Дополним до полных квадратов выражения в скобках:

или 
Окончательно получим

Произведём параллельный перенос осей координт  , полагая
, полагая
 .
.
Получим в результате каноническое уравнение кривой в системе координаи  с началом в точке
с началом в точке  :
:
4  ,
,
где коэффициенты при квадратах переменных есть собственные числа матрицы
S. Разделив обе части этого уравнения на 36 получим в итоге каноническое уравнение эллипса в системе координат  :
:

с полуосями a =3 и b =2, как это следует из уранения (5.14) эллипса.
Пример2.14 выяснить характер кривой:


Решение. Здесь с учётом формулы (8.14) нахдим 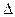 =9
=9  16 -
16 -  =0,т.е. это кривая параболического типа. Матрица из коэффициентов квадратичной формы
=0,т.е. это кривая параболического типа. Матрица из коэффициентов квадратичной формы  . Составляем характеристическое уравнение этой матрицы:
. Составляем характеристическое уравнение этой матрицы:
 или
или  т.е.
т.е.  - собственные числа.
- собственные числа.
Для нахождения соответствующих этим числам собственных векторов матрицы S запишем ОСЛАУ вида:

Полагая 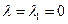 , получаем систему уранений
, получаем систему уранений

Решая эту систему, находим собственный вектор  матрицы S, а при
матрицы S, а при  получаем из ОСЛАУ систему уравнений
получаем из ОСЛАУ систему уравнений

Из этой системы находим второй собственный вектор  .Нормируя эти собственные векторы получим ортонормированный базис в Е2 из ортов-векторов
.Нормируя эти собственные векторы получим ортонормированный базис в Е2 из ортов-векторов  и
и  ,т.к. скалярное произведение их (
,т.к. скалярное произведение их (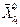

 )=0.
)=0.
Ортогональная матрица 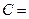 (
(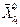 ,
,  ) преобразования координат при переходе к этому базису имеет вид
) преобразования координат при переходе к этому базису имеет вид  ,
,  .Поэтому формулы преобразования координат запишутся в виде:
.Поэтому формулы преобразования координат запишутся в виде:

Перепишем данное уравнение кривой в виде

Подставляя полученные значения 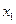 и
и 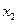 в это уравнение, найдём уравнение кривой отнсительно прямоугольной декартовой системы координат
в это уравнение, найдём уравнение кривой отнсительно прямоугольной декартовой системы координат  в Е2 :
в Е2 :
25 
Приведя подобные члены и сократив на 25, приходим к уравнению

Перепишем это уравнение в виде  . Для этого произведём па-
. Для этого произведём па-
параллельный перенос системы координат  , приняв за новое начало коор-
, приняв за новое начало коор-
динт точку  В итоге получим каноническое уравнение заданной кривой
В итоге получим каноническое уравнение заданной кривой
:  .
.
в новой системе координат  . Это есть каноническое уравнение (7.14) в системе координат
. Это есть каноническое уравнение (7.14) в системе координат  параболы с параметром p =5.
параболы с параметром p =5.



 , на которой введена прямоугольная декартова система координат
, на которой введена прямоугольная декартова система координат 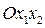 , общее уравнение кривой второго порядка:
, общее уравнение кривой второго порядка: , (1.14)
, (1.14) - заданные действительные числа, для которых выполняется неравенство:
- заданные действительные числа, для которых выполняется неравенство: , (2.14)
, (2.14) , (3.14)
, (3.14)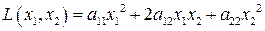 (4.14)
(4.14) .Из аналитической геометрии известно,что основными невырожденными кривыми второго порядка на плоскости
.Из аналитической геометрии известно,что основными невырожденными кривыми второго порядка на плоскости  и
и 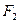 , называмых фокусами эллипса, есть величина постоянная, равная 2 a.
, называмых фокусами эллипса, есть величина постоянная, равная 2 a. и
и 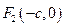 на координатной оси
на координатной оси 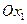 , то получим простейшее (каноническое) уравнение эллипса:
, то получим простейшее (каноническое) уравнение эллипса: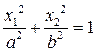 , (5.14)
, (5.14) (6.14)
(6.14) координатой оси
координатой оси 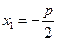 - директрисой параболы, то получим каноническое уравнение параболы:
- директрисой параболы, то получим каноническое уравнение параболы: (7.14)
(7.14) , (8.14)
, (8.14)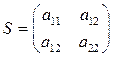 квадратичной формы
квадратичной формы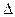 не меняется при преобразовании координат на плоскости, поэтому её называют инвариантом кривой второго порядка..
не меняется при преобразовании координат на плоскости, поэтому её называют инвариантом кривой второго порядка.. к ортонормированному базису, состоящему из собственных векторов
к ортонормированному базису, состоящему из собственных векторов  матрицы S,
матрицы S, , где
, где  - собственные числа матрицы S. Этот переход совершается с помощью ортогональной матрицы
- собственные числа матрицы S. Этот переход совершается с помощью ортогональной матрицы 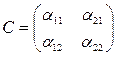 ,
,  , преобразования переменных:
, преобразования переменных: 
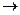
 . В результате этого квадратичная форма
. В результате этого квадратичная форма 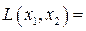 =
= 
 приводится к каноническому виду
приводится к каноническому виду 
 +
+ 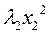 . При переходе от матрицы S к диагональной матрице B величина
. При переходе от матрицы S к диагональной матрице B величина 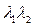 . На основании этого имеет место
. На основании этого имеет место =
=  , либо эллипс при
, либо эллипс при  , приводят в итоге уравнение кривой к требуемому каноническому виду.
, приводят в итоге уравнение кривой к требуемому каноническому виду.
 8 -
8 -  =36>0, т.е. это кривая эллиптического типа. Здесь матрица
=36>0, т.е. это кривая эллиптического типа. Здесь матрица  . Приведём её к диагональному виду. Для этого составим характеристическое уравнение этой матрицы:
. Приведём её к диагональному виду. Для этого составим характеристическое уравнение этой матрицы: , т.е.
, т.е.  .
. Для нахождения соответствующих им собственных векторов запишем ОСЛАУ:
Для нахождения соответствующих им собственных векторов запишем ОСЛАУ: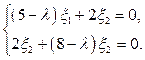
 для определения соответствующего собственного вектора
для определения соответствующего собственного вектора  получаем систему уравнений
получаем систему уравнений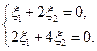
 . Полагая
. Полагая  находим
находим  и
и 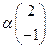 .Нормируя этот вектор, получим его орт-вектор
.Нормируя этот вектор, получим его орт-вектор  . Полагая
. Полагая 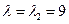 , получаем из ОСЛАУ для определения второго собственного вектора
, получаем из ОСЛАУ для определения второго собственного вектора  систему уравнений
систему уравнений
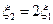 . Полагая
. Полагая 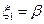 , находим
, находим  . Нормируя
. Нормируя  .
.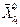 и
и  ортогональные, т.к. их скалярное произведение (
ортогональные, т.к. их скалярное произведение (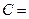 (
(
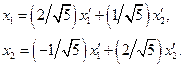
 и
и  выражения, подставим в общее уравнение кривой:
выражения, подставим в общее уравнение кривой: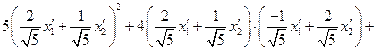
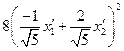 -
-




 , полагая
, полагая .
. с началом в точке
с началом в точке  :
: ,
,


 =0,т.е. это кривая параболического типа. Матрица из коэффициентов квадратичной формы
=0,т.е. это кривая параболического типа. Матрица из коэффициентов квадратичной формы  . Составляем характеристическое уравнение этой матрицы:
. Составляем характеристическое уравнение этой матрицы: или
или  т.е.
т.е.  - собственные числа.
- собственные числа.
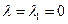 , получаем систему уранений
, получаем систему уранений
 матрицы S, а при
матрицы S, а при  получаем из ОСЛАУ систему уравнений
получаем из ОСЛАУ систему уравнений
 .Нормируя эти собственные векторы получим ортонормированный базис в Е2 из ортов-векторов
.Нормируя эти собственные векторы получим ортонормированный базис в Е2 из ортов-векторов  и
и  ,т.к. скалярное произведение их (
,т.к. скалярное произведение их ( ,
, 

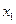 и
и 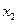 в это уравнение, найдём уравнение кривой отнсительно прямоугольной декартовой системы координат
в это уравнение, найдём уравнение кривой отнсительно прямоугольной декартовой системы координат  в Е2 :
в Е2 :

 . Для этого произведём па-
. Для этого произведём па- В итоге получим каноническое уравнение заданной кривой
В итоге получим каноническое уравнение заданной кривой .
.


