Согласно определения6.1.. матрица А =  =
= 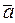 называется вектором-строкой. Действительные (вещественные) числа
называется вектором-строкой. Действительные (вещественные) числа 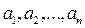 называют координатами вектора
называют координатами вектора 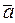 , а число n - его размерностью. Множество А n всех n – мерных векторов называется n – мерным векторным (арифметическим или числовым) пространством. Над векторами, как и над матрицами, можно производить линейные операции:1) сложение двух векторов
, а число n - его размерностью. Множество А n всех n – мерных векторов называется n – мерным векторным (арифметическим или числовым) пространством. Над векторами, как и над матрицами, можно производить линейные операции:1) сложение двух векторов  = (a 1 + b 1 , a 2 + b 2 ,…, an + b n) и 2) умножение вектора
= (a 1 + b 1 , a 2 + b 2 ,…, an + b n) и 2) умножение вектора 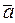 на вещественное число
на вещественное число 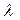 ÎR, т.е.
ÎR, т.е. 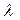
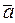 =
= 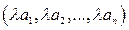 , которые обладают свойствами линейности (1.1) для матриц. Поэтому векторное пространство А n называют также линейным пространством. При этом существует единственный нулевой вектор
, которые обладают свойствами линейности (1.1) для матриц. Поэтому векторное пространство А n называют также линейным пространством. При этом существует единственный нулевой вектор  , удовлетворяющий условию
, удовлетворяющий условию 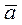 + (-
+ (- 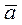 ) =
) = 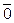 .
.
Имеются многие типы математических объектов различной природы, для которых можно тоже каким либо способом ввести операции сложения их элементов и умножения на число, не выводящие за пределы исходного множества. С учётом этого даётся следующее
Определения1.6. Множество X элементов 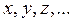 , в котором 1)для любых двух элементов
, в котором 1)для любых двух элементов  и
и  определены операция сложения
определены операция сложения 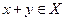 и 2)для любого элемента
и 2)для любого элемента  и любого действительного числа
и любого действительного числа 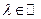 определено произведение
определено произведение  , обладающие свойством линейности:
, обладающие свойством линейности:
1.  ;
;
2.  ;
;
3.существует такой элемент 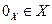 (нуль-элемент), что
(нуль-элемент), что  для любого
для любого  ;
;
4.для каждого элемента  существует элемент
существует элемент  такой, что
такой, что 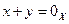 ,т.е.
,т.е. 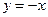 -противоположный элемент для
-противоположный элемент для  ;
;
5.1 
 =
=  ;
;
6. 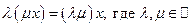 ;
;
7. 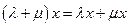 ;
;
8. 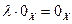

называется линейным (абстрактным) векторным пространством. Элементы из  называют также векторами,а числа из вещественного множества
называют также векторами,а числа из вещественного множества  - скалярами.
- скалярами.
На основании этих свойств получаются непосредственно следующие следствия:
1.В каждом линейном пространстве Х существует только один нуль- элемент 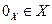 .
.
2.Для каждого элемента  существует только один противоположный элемент
существует только один противоположный элемент 
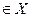 .
.
3.Для каждого элемента  выполняется равенство
выполняется равенство  .
.
4.Для любого 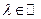 и
и 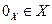 выполняется равенство
выполняется равенство 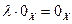 .
.
5.Из равенства 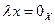 следует либо
следует либо  или
или 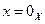 .
.
6.Элемент  является противоположным для элемента
является противоположным для элемента  .
.
Покажем, например, справедливость свойства 2.Допустим, что имеется другой противоположный элемент t 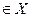 для элемента
для элемента  , т.е.
, т.е.  . Тогда,прибавляя к обеим частям этого равенствавектор
. Тогда,прибавляя к обеим частям этого равенствавектор  , получим:
, получим:
 или
или 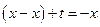 , откуда вытекает, что
, откуда вытекает, что 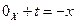 и, следовательно,
и, следовательно,  .
.
Пример1.6. Многочлены 1-ой степени Р  = ax + b, где
= ax + b, где  образуют линейное пространство Х, для которого
образуют линейное пространство Х, для которого 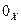 =
= 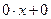
Пример2.6 Множество матриц 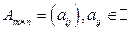 , относительно операций сложения и умножения на число образует линейное пространство в силу свойства линейности этих операций (1.1).
, относительно операций сложения и умножения на число образует линейное пространство в силу свойства линейности этих операций (1.1).
Пример3.6 Пространство R, элементами которого являются всевозможные дифференцируемые функции  обращающиеся в нуль при t =0, и пространство
обращающиеся в нуль при t =0, и пространство 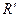 , элементами которого являются производные функций, принадлежащих пространству R, т.е
, элементами которого являются производные функций, принадлежащих пространству R, т.е 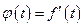 , где
, где  , являются линейными пространствами.
, являются линейными пространствами.
В векторном пространстве А n можно ввести, на основе правила умножения матриц, правило умножения двух векторов 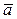 и
и 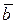 по формуле:
по формуле:
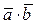 =
= 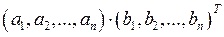 =
= 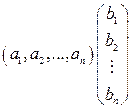 = =
= = 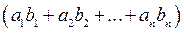 .
.
Отсюда в силу определения 7.1 одноэлементной матрицы получаем формулу вида:
(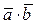 ) =
) = 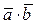 =
= 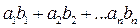 , (1.6)
, (1.6)
которую называют скалярным произведением двух векторов в А n. Из формулы (1.6) вытекают свойства скалярного произведения:
1. (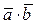 ) = (
) = (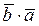 );
);
2.  , где
, где 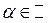 ;
;
3.  ;
;
4.  >0;
>0;
5. 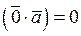 для любого вектора
для любого вектора 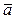 .
.
Определение2.6. Векторы  и
и  называют ортогональными, если их скалярное произведение равно нулю:
называют ортогональными, если их скалярное произведение равно нулю: 

 = 0.
= 0.
Определение3.6. Длиной или модулем вектора  называется величина
называется величина
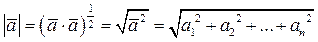 (2.6)
(2.6)
Если 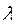 - любое вещественное число, то
- любое вещественное число, то  для любого
для любого  .
.
Определение4.6. Вектор  называется нормированным или вектором единичной длины, если его модуль
называется нормированным или вектором единичной длины, если его модуль  = 1.
= 1.
Чтобы нормировать вектор  достаточно умножить его на вещественное число
достаточно умножить его на вещественное число  . В результате получим орт-вектор
. В результате получим орт-вектор  0 для вектора
0 для вектора  .
.
Определение5.6. Попарно ортогональные и нормированные векторы называют ортонормированными.
Например, такими являются векторы 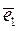 =
=  ,
,  =
=  ,…,
,…,  = =
= = 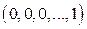 .
.
В пространстве А n по формуле
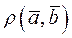 =
= 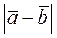 =
=  (3.6)
(3.6)
можно ввести расстояние между векторами 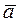 и
и  или евклидову метрику, которое удовлетворяет трём аксиомам метрического пространства:
или евклидову метрику, которое удовлетворяет трём аксиомам метрического пространства:
1. 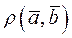 = 0 тогда и только тогда, когда
= 0 тогда и только тогда, когда  =
=  ;
;
2. 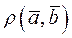 =
= 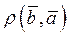 - свойство симметрии;
- свойство симметрии;
3. 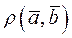
 - неравенство треугольника.
- неравенство треугольника.
Определение6.6. Векторное пространство А n с евклидовой метрикой (3.6) называется n – мерным евклидовым пространством E n.
Замечание1.6. По формуле (3.6) находится расстояние между точками M 1 (a 1, a 2 …, a n) и M 2 (b 1 , b 2 ,…, b n) в евклидовом пространстве E n, в котором введена прямоугольная декартова система координат Ox 1 x 2 … x n и, в частности, вычисляется расстояние между точками на обычной плоскости E 2 или в трёхмерном пространстве E 3 .Из форму (2.6) и (3.6) следует также, что  -
- 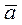 =
=  , где вектор
, где вектор  геометрически представляет собой направленный отрезок прямой с началом в точке M 1 (a 1, a 2, …, a n) и с концом в точке M 2 (b 1 , b 2 ,…, b n) в евклидовом пространстве E n, а сам вектор
геометрически представляет собой направленный отрезок прямой с началом в точке M 1 (a 1, a 2, …, a n) и с концом в точке M 2 (b 1 , b 2 ,…, b n) в евклидовом пространстве E n, а сам вектор 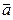 =
=  есть радиус – вектор точки М1 В частности, если начало и конец вектора
есть радиус – вектор точки М1 В частности, если начало и конец вектора  совпадают, то имеем нуль-вектор
совпадают, то имеем нуль-вектор  =
= 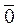 = (0,0,…,0).
= (0,0,…,0).
Замечание2.6. Рассмотрим справедливое при любом 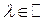 неравенство
неравенство 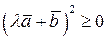 , где
, где  и
и 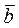 векторы евклидова пространства E n. Возводя левую часть его в квадрат, получим неравенство вида
векторы евклидова пространства E n. Возводя левую часть его в квадрат, получим неравенство вида
 . (4.6)
. (4.6)
Для того, чтобы неравенство (4.6) имело место, необходимо и достаточно чтобы выполнялось условие  или
или
 . (5.6)
. (5.6)
Неравенство (5.6) называется неравенством Коши - Буняковского. Оно выполняется для любых векторов пространства E n, в котором введено скалярное произведение двух векторов. Из неравенств (2.6) и (5.6) следует, что  . На основании этого неравенства вводится угол
. На основании этого неравенства вводится угол  между векторами
между векторами 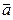 и
и 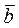 евклидова пространства E n по формуле
евклидова пространства E n по формуле
 , (6.6)
, (6.6)
где 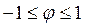 . Если
. Если 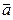 и
и 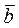 - ненулевые векторы, т.е.
- ненулевые векторы, т.е. 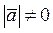 и
и 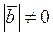 , а
, а 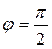 ,
,
то из (6.6) вытекает, что скалярное произведение  = 0. Поэтому говорят, что векторы
= 0. Поэтому говорят, что векторы 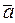 и
и 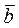 ортогональны в евклидовом пространстве E n и пишут
ортогональны в евклидовом пространстве E n и пишут  .
.
Пример4.6 Даны векторы 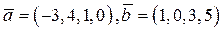 в евклидовом 4-мерном пространстве E 4 .Найти скалярное произведение этих векторов, длины их, расстояние
в евклидовом 4-мерном пространстве E 4 .Найти скалярное произведение этих векторов, длины их, расстояние 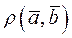 , угол
, угол 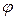 между ними и орт – вектор
между ними и орт – вектор  0 для вектора
0 для вектора  .. Решение. На основании выше данных определений в §6 находим:
.. Решение. На основании выше данных определений в §6 находим:
1).скалярное произведение 

 =
= 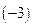
 1+4
1+4  0+1
0+1  3+0
3+0  5=5;
5=5;
2)длины 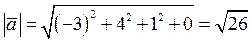 и
и 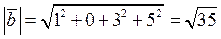 векторов
векторов
 и
и  ;
;
3) расстояние 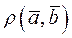 =
= 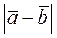 =
=  ;
;
4) по формуле (6.6)полчаем, что 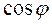 =
= 
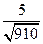 ,т.е.
,т.е. 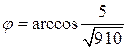 ;
;
4)орт-вектор  0 =
0 = 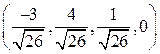 .
.
Пример5.6 Найти в пространстве E 3 вектор с началом в точке M 1 (2,-4, 3) и концом в точке M 2 (3,7,1).
Решение. На основании Замечания 1.6. получаем в E 3 вектор  = (2- 3, -4-7, 3-5)= (-1,-11, 2).
= (2- 3, -4-7, 3-5)= (-1,-11, 2).



 =
= 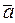 называется вектором-строкой. Действительные (вещественные) числа
называется вектором-строкой. Действительные (вещественные) числа 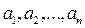 называют координатами вектора
называют координатами вектора  = (a 1 + b 1 , a 2 + b 2 ,…, an + b n) и 2) умножение вектора
= (a 1 + b 1 , a 2 + b 2 ,…, an + b n) и 2) умножение вектора 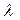 ÎR, т.е.
ÎR, т.е. 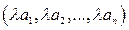 , которые обладают свойствами линейности (1.1) для матриц. Поэтому векторное пространство А n называют также линейным пространством. При этом существует единственный нулевой вектор
, которые обладают свойствами линейности (1.1) для матриц. Поэтому векторное пространство А n называют также линейным пространством. При этом существует единственный нулевой вектор  , удовлетворяющий условию
, удовлетворяющий условию 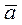 + (-
+ (- 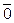 .
.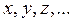 , в котором 1)для любых двух элементов
, в котором 1)для любых двух элементов  и
и  определены операция сложения
определены операция сложения 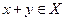 и 2)для любого элемента
и 2)для любого элемента 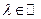 определено произведение
определено произведение  , обладающие свойством линейности:
, обладающие свойством линейности: ;
; ;
;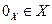 (нуль-элемент), что
(нуль-элемент), что  для любого
для любого 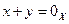 ,т.е.
,т.е. 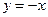 -противоположный элемент для
-противоположный элемент для 
 =
= 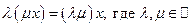 ;
;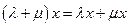 ;
;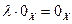

 называют также векторами,а числа из вещественного множества
называют также векторами,а числа из вещественного множества  - скалярами.
- скалярами.
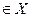 .
. .
.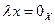 следует либо
следует либо  или
или 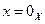 .
. является противоположным для элемента
является противоположным для элемента  . Тогда,прибавляя к обеим частям этого равенствавектор
. Тогда,прибавляя к обеим частям этого равенствавектор  , получим:
, получим: или
или 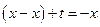 , откуда вытекает, что
, откуда вытекает, что 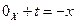 и, следовательно,
и, следовательно,  .
. = ax + b, где
= ax + b, где  образуют линейное пространство Х, для которого
образуют линейное пространство Х, для которого 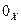 =
= 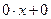
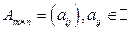 , относительно операций сложения и умножения на число образует линейное пространство в силу свойства линейности этих операций (1.1).
, относительно операций сложения и умножения на число образует линейное пространство в силу свойства линейности этих операций (1.1). обращающиеся в нуль при t =0, и пространство
обращающиеся в нуль при t =0, и пространство 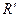 , элементами которого являются производные функций, принадлежащих пространству R, т.е
, элементами которого являются производные функций, принадлежащих пространству R, т.е 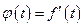 , где
, где  , являются линейными пространствами.
, являются линейными пространствами.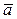 и
и 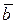 по формуле:
по формуле: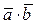 =
= 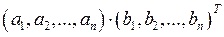 =
= 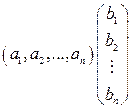 = =
= = 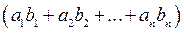 .
.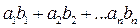 , (1.6)
, (1.6)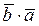 );
); , где
, где 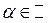 ;
; ;
; >0;
>0;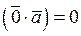 для любого вектора
для любого вектора 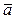 .
. и
и  называют ортогональными, если их скалярное произведение равно нулю:
называют ортогональными, если их скалярное произведение равно нулю: 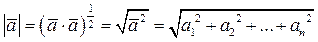 (2.6)
(2.6)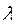 - любое вещественное число, то
- любое вещественное число, то  для любого
для любого  = 1.
= 1. . В результате получим орт-вектор
. В результате получим орт-вектор 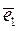 =
=  ,
,  =
=  ,…,
,…,  = =
= = 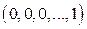 .
.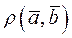 =
= 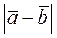 =
=  (3.6)
(3.6)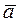 и
и 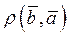 - свойство симметрии;
- свойство симметрии; - неравенство треугольника.
- неравенство треугольника. , где вектор
, где вектор 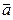 =
=  есть радиус – вектор точки М1 В частности, если начало и конец вектора
есть радиус – вектор точки М1 В частности, если начало и конец вектора 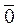 = (0,0,…,0).
= (0,0,…,0).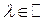 неравенство
неравенство 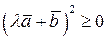 , где
, где  и
и 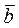 векторы евклидова пространства E n. Возводя левую часть его в квадрат, получим неравенство вида
векторы евклидова пространства E n. Возводя левую часть его в квадрат, получим неравенство вида . (4.6)
. (4.6) или
или . (5.6)
. (5.6) . На основании этого неравенства вводится угол
. На основании этого неравенства вводится угол  между векторами
между векторами  , (6.6)
, (6.6)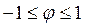 . Если
. Если 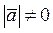 и
и 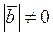 , а
, а 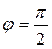 ,
, = 0. Поэтому говорят, что векторы
= 0. Поэтому говорят, что векторы  .
.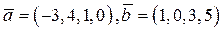 в евклидовом 4-мерном пространстве E 4 .Найти скалярное произведение этих векторов, длины их, расстояние
в евклидовом 4-мерном пространстве E 4 .Найти скалярное произведение этих векторов, длины их, расстояние 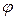 между ними и орт – вектор
между ними и орт – вектор 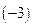
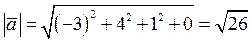 и
и 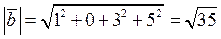 векторов
векторов ;
;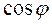 =
= 
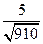 ,т.е.
,т.е. 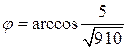 ;
;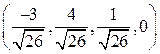 .
.

