

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Определение1.3. Системой из m линейных алгебраических уравнений с n неизвестными  называется система вида
называется система вида
 , (1.3)
, (1.3)
Числа  ,
,  -называют коэффициентами системы, а числа
-называют коэффициентами системы, а числа 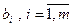 - её свободными членами. Систему (1.3) называют кратко иногда СЛАУ.
- её свободными членами. Систему (1.3) называют кратко иногда СЛАУ.
Определение2.3. Решением СЛАУ (1.3) называется n значений неизвестных 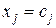 ,
, 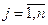 , при подстановке которых в систему (1.3) все её уравнения обращаются в верные числовые равенства
, при подстановке которых в систему (1.3) все её уравнения обращаются в верные числовые равенства 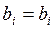 ,
,  .
.
Определение3.3.. СЛАУ (1.3) называется совместной, если она имеет хотя бы одно решение.
Определение4.3. СЛАУ (1.3.) называется несовместной, если она не имеет ни одного решения.
Определение 5.3. Если СЛАУ (1.3) имеет более одного решения, то каждое ее решение называют частным.
Определение 6.3. Совокупность всех частных решений называется общим решением СЛАУ (1.3).
Решит ь СЛАУ (1.3) это значит
1) выяснить совместна она или нет;
2) найти общее решение в случае, когда СЛАУ (1.3) – совместна.
Рассмотрим основные методы решения СЛАУ. Изучим сначала матричный метод решения СЛАУ.
Возьмем матрицу  , составленную из коэффициентов
, составленную из коэффициентов  системы (1.3), т.е.
системы (1.3), т.е.
 ,
,
затем вектор-столбец

из неизвестных 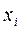 ,
, 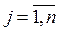 , этой системы и вектор-столбец
, этой системы и вектор-столбец
 ,
,
состоящий из её свободных членов bi, 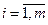 . Тогда данную СЛАУ (1.3) с учетом правила умножения матриц можно записать коротко в матричном виде
. Тогда данную СЛАУ (1.3) с учетом правила умножения матриц можно записать коротко в матричном виде
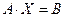 . (2.3)
. (2.3)
.
Определение7.3. Если  , то СЛАУ (1.3) называют квадратно й, а если
, то СЛАУ (1.3) называют квадратно й, а если  , то однородной или ОСЛАУ.
, то однородной или ОСЛАУ.
Пусть А - квадратная матрица, для которой  , т.е. существует обратная матрица А -1. Тогда, умножая обе части матричного равенства (2.3) слева на А -1, получим
, т.е. существует обратная матрица А -1. Тогда, умножая обе части матричного равенства (2.3) слева на А -1, получим
|
|
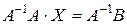 .
.
Так как  и
и 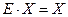 , то имеем отсюда, что
, то имеем отсюда, что
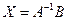 (3.3)
(3.3)
Это решение квадратной системы (1.3) в матричной форме, когда  .
.
Пример.1.3. Найти решение СЛАУ
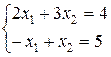 .
.
Решение. Здесь  . Следовательно, на основании фор-
. Следовательно, на основании фор-
мулы (3.3) получим
 , т.е.
, т.е. 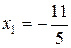 ;
; 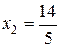 .
.
Рассмотрим затем метод Крамера для нахождения решения квадратной СЛАУ. Для этого запишем формулу (3.3) в развёрнутом матричном виде:
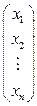 =
= 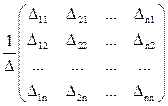 .
. 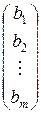 , (4.3)
, (4.3)
где  - алгебраические дополнения для элементов а ij, i, j =1,2,…, п, матрицы A = (a ij) квадратной СЛАУ. Применяя правило умножения матриц и правило умножения матрицы на число, получим из (4.3.), что
- алгебраические дополнения для элементов а ij, i, j =1,2,…, п, матрицы A = (a ij) квадратной СЛАУ. Применяя правило умножения матриц и правило умножения матрицы на число, получим из (4.3.), что
 =
= 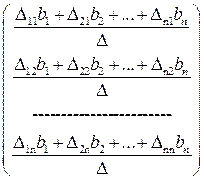 (5.3)
(5.3)
и, следовательно, на основании определения равенства матриц находим из (5.3)

где! i, i = 1,2,…, n, - определители вида
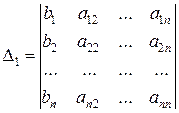 ,
, 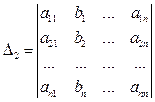 , …,
, …, 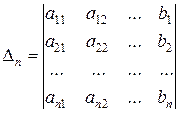 ,
,
которые получаются из определителя 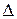 матрицы А n ‰ n путем замены его i -го столбца
матрицы А n ‰ n путем замены его i -го столбца  вектором-столбцом свободных членов
вектором-столбцом свободных членов 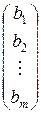 .Таким образом, по-
.Таким образом, по-
лучаем формулы Крамера для решения квадратной СЛАУ:
 , i = 1,2,…, n. (6.3)
, i = 1,2,…, n. (6.3)
Пример2.3. Решить СЛАУ  , применяя метод Крамера.
, применяя метод Крамера.
Решение. На основании формул (6.3) находим в данном случае, что
 ;
;
 ;
;  ;
;
т.е. 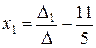 ;
; 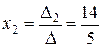 .
.
Замечание1. 3. Метод Крамера применим в общем случае и для СЛАУ вида (1.3), когда матрица  из её коэффициентов – прямоугольная. В этом случае следует найти какой-либо базисный минор
из её коэффициентов – прямоугольная. В этом случае следует найти какой-либо базисный минор 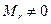 порядка r
порядка r  матрицы
матрицы 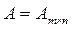 , состоящей из коэффициентов системы (1.3), и взять r её уравнений, которые содержат коэффициенты, входящие в минор
, состоящей из коэффициентов системы (1.3), и взять r её уравнений, которые содержат коэффициенты, входящие в минор 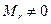 , а остальные уравнения из (1.3) отбросить. Неизвестные
, а остальные уравнения из (1.3) отбросить. Неизвестные  , вместе с коэффициентами, входящими в
, вместе с коэффициентами, входящими в 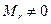 оставляют слева, а остальные неизвестные
оставляют слева, а остальные неизвестные 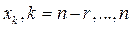 , вместе с коэффициентами перед ними переносят в правые части полученных r уравнений. Например, рассмотрим СЛАУ вида:
, вместе с коэффициентами перед ними переносят в правые части полученных r уравнений. Например, рассмотрим СЛАУ вида:
|
|
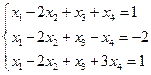
Запишем прямоугольную матрицу  из коэффициентов этой системы. Для неё все миноры третьего порядка
из коэффициентов этой системы. Для неё все миноры третьего порядка  равны нулю, т.к. они имеют пропорциональные столбцы, и значит ранг этой матрицы
равны нулю, т.к. они имеют пропорциональные столбцы, и значит ранг этой матрицы  < 3.Среди миноров второго порядка этой матрицы А имеются отличные от нуля, например, минор второго порядка
< 3.Среди миноров второго порядка этой матрицы А имеются отличные от нуля, например, минор второго порядка  , составленный из коэффициентов перед неизвестными
, составленный из коэффициентов перед неизвестными  и x 4. Принимая этот минор M 2 за базисный, перепишем данную СЛАУ в виде:
и x 4. Принимая этот минор M 2 за базисный, перепишем данную СЛАУ в виде:
 или
или  .
.
Отсюда получаем общее решение
системы вида  , которое зависит от произвольных неизвестных
, которое зависит от произвольных неизвестных
x 1 и x 2. Полагая, например, x 1 = 0, x 2 = 0, получим одно из частных решений этой системы: x1 =0, x2 =0, x3 = 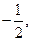
 .
.
Определение8.3. Матрица вида
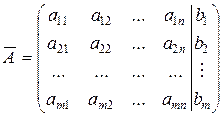
называется расширенной матрицей системы линейных алгебраических уравнений (1.3).Она получается путём добавления к матрице  системы (1.3) вектора-столбца
системы (1.3) вектора-столбца 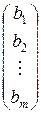 свободных членов этой СЛАУ (1.3).
свободных членов этой СЛАУ (1.3).
Ответ в общем случае на вопрос о совместности СЛАУ (1.3) дает
Теорема 1.3. (Кронекера-Капелли ). Система линейных алгебраических уравнений (1.3) совместна тогда и только тогда, когда  , т.е. ранг расширенной матрицы
, т.е. ранг расширенной матрицы  системы (1.3) равен рангу основной матрицы А этой системы.
системы (1.3) равен рангу основной матрицы А этой системы.
Определение. 9.3.. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Теорема.2.3. Если система (1.3) совместна и  , где n –число её неизвестных
, где n –число её неизвестных  ,
,  , то она имеет единственное решение, т.е. является определенной.
, то она имеет единственное решение, т.е. является определенной.
Теорема 3. 3.. Если система (1.3) совместна, а 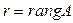 < n, то она имеет бесконечное множество решений, т.е. является неопределенной.
< n, то она имеет бесконечное множество решений, т.е. является неопределенной.
Замечание2.3. Однородная система (ОСЛАУ) всегда совместна, так как для неё  , и потому она имеет единственное тривиальное (нулевое) решение
, и потому она имеет единственное тривиальное (нулевое) решение 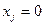 ,
, 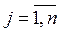 , когда
, когда  .
.
Определение 10.3. Две системы СЛАУ (1.3) называют эквивалентными, если они имеют одно и то же решение.
Эквивалентные СЛАУ в частности получаются при элементарных преобразованиях данной системы (1.3) при условии, что эти преобразования выполняются лишь над строками расширенной матрицы  этой системы.
этой системы.
Примечание. Нахождение решения СЛАУ (1.3) как по методу обратной матрицы (3.3) так и по методу Крамера (6.3) являются очень трудоёмкими операциями, когда 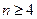 . Для их выполнения требуется порядка n 2 n! арифметических действий. Например, при n =5 получается около 3000 действий, а при n =10 требуется выполнить 3,6
. Для их выполнения требуется порядка n 2 n! арифметических действий. Например, при n =5 получается около 3000 действий, а при n =10 требуется выполнить 3,6  108 действий. При n =100 потребуется потратить очень много времени даже суперкомпьютерам для вычисления решения СЛАУ. Помимо этого погрешности компьютерного округления приводят в итоге к большим ошибкам в численных расчётах для СЛАУ большого порядка.
108 действий. При n =100 потребуется потратить очень много времени даже суперкомпьютерам для вычисления решения СЛАУ. Помимо этого погрешности компьютерного округления приводят в итоге к большим ошибкам в численных расчётах для СЛАУ большого порядка.
|
|
Более экономичным методом решения СЛАУ является метод Гаусса, основанный на приведении расширенной матрицы  для СЛАУ (1.3) путем элементарных преобразований над её строками к ступенчатому виду (в частности к треугольному). Поэтому метод Гаусса является предпочтительным при нахождении решения СЛАУ, которые имеют большой порядок n. При этом, когда расширенную матрицу
для СЛАУ (1.3) путем элементарных преобразований над её строками к ступенчатому виду (в частности к треугольному). Поэтому метод Гаусса является предпочтительным при нахождении решения СЛАУ, которые имеют большой порядок n. При этом, когда расширенную матрицу  приводят к ступенчатому виду, удобно, чтобы
приводят к ступенчатому виду, удобно, чтобы 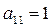 . Для этого следует либо переставить местами уравнения в (1.3), либо разделить обе части первого уравнения на
. Для этого следует либо переставить местами уравнения в (1.3), либо разделить обе части первого уравнения на  . Если в процессе приведения матрицы
. Если в процессе приведения матрицы 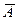 к ступенчатому виду при элементарных преобразованиях над ее строками появятся нулевые строки, то соответствующие им равенства
к ступенчатому виду при элементарных преобразованиях над ее строками появятся нулевые строки, то соответствующие им равенства 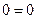 в СЛАУ (1.3) отбрасывают. Если же появятся уравнения вида
в СЛАУ (1.3) отбрасывают. Если же появятся уравнения вида  , где
, где 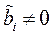 , то это говорит в силу теоремы 1.3 (Кронекера-Капелли) о несовместности системы (1.3), так как в этом случае
, то это говорит в силу теоремы 1.3 (Кронекера-Капелли) о несовместности системы (1.3), так как в этом случае 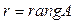 <
< 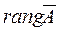 .
.
Замечание3.3. Если r < n и СЛАУ (1.3) совместна, то общее решение СЛАУ (1.3) содержит  неизвестных
неизвестных 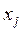 ,
,  , которые выбираются произвольно, и они являются параметрами решения, а остальные r неизвестных
, которые выбираются произвольно, и они являются параметрами решения, а остальные r неизвестных 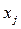 ,
, 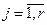 , определяются единственным образом через эти свободные неизвестные. Их число r равно рангу матрицы А системы и потому они являются базисными.
, определяются единственным образом через эти свободные неизвестные. Их число r равно рангу матрицы А системы и потому они являются базисными.
Процесс решения СЛАУ (1.3) по методу Гаусса состоит из двух этапов. На первом этапе СЛАУ (1.3) приводят путём элементарных преобразований её расширенной матрицы  к ступенчатому виду:
к ступенчатому виду:

 (7.3)
(7.3)
где k £ m, а 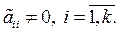 Здесь
Здесь 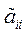 являются главными элементами системы (7.3). Так как при этом
являются главными элементами системы (7.3). Так как при этом 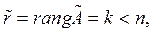 где
где  - ступенчатая матрица, составленная из элементов
- ступенчатая матрица, составленная из элементов  системы (7.3), то неизвестные
системы (7.3), то неизвестные 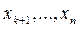 объявляются свободными, а неизвестные
объявляются свободными, а неизвестные  - базисными. Тогда систему (7.3) относительно этих базисных неизвестных
- базисными. Тогда систему (7.3) относительно этих базисных неизвестных  можно записать в виде:
можно записать в виде:
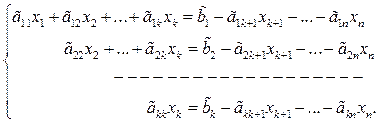 (7.4)
(7.4)
На втором этапе (обратный ход) идёт последовательное нахождение базисных неизвестных из системы (7.4)., т.е. вначале вычисляют из последнего уравнения системы (7.4) неизвестное  , а затем и все остальные базисные неизвестные
, а затем и все остальные базисные неизвестные 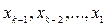 . Они выражаются через свободные неизвестные
. Они выражаются через свободные неизвестные  . Придавая этим свободным неизвестным произвольные числовые значения, будем получать частные решения системы (1.3).
. Придавая этим свободным неизвестным произвольные числовые значения, будем получать частные решения системы (1.3).
|
|
Если ступенчатая система (7.3) окажется треугольной, т.е. k = n, то исходная система (1.3) имеет единственное решение.
Пример3.3 Решить методом Гаусса СЛАУ вида

Здесь число неизвестных n = 4.
Решение. Приведём расширенную матрицу  этой СЛАУ путём элементарных преобразований нал её строками к ступенчатому виду
этой СЛАУ путём элементарных преобразований нал её строками к ступенчатому виду

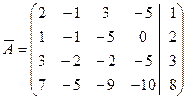 ~
~ 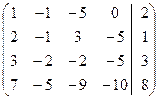 ~
~
~ 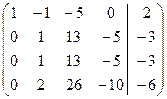 ~
~ 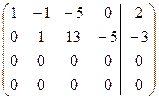
На основании этого СЛАУ запишется в эквивалентном ступенчатом виде:
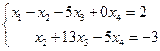
Так как для матрицы A данной системы её ранг 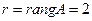 < 4, то эта система имеет бесконечное множество решений, из которых 2 являются базисными. Положим
< 4, то эта система имеет бесконечное множество решений, из которых 2 являются базисными. Положим 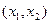 за базисное решение, так как в матрице A системы имеется соответствующий им базисный минор
за базисное решение, так как в матрице A системы имеется соответствующий им базисный минор  ¹.0. Тогда полученную систему запишем в эквивалентном виде:
¹.0. Тогда полученную систему запишем в эквивалентном виде:
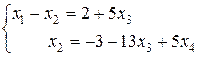 .
.
Из этой системы обратным ходом находим базисные неизвестные
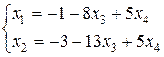 .
.
Здесь 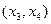 - свободные неизвестные или параметры. Если положить
- свободные неизвестные или параметры. Если положить  , то получим соответствующее частное решение системы
, то получим соответствующее частное решение системы
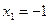 ;
; 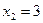 ;
;  ;
;  .
.
Пример4.3. Решить методом Гаусса СЛАУ

Решение. Приведём расширенную матрицу  этой СЛАУ с помощью элементарных преобразований над её строками к ступенчатому виду:
этой СЛАУ с помощью элементарных преобразований над её строками к ступенчатому виду:
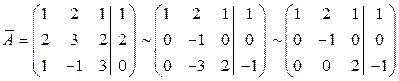 .
.
На основании этого СЛАУ запишется в эквивалентном треугольном виде:

Отсюда методом обратного хода получаем её единственное решение:
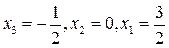 .
.
|
|
|

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!