Изучим методы решения сравнений:  ,
,
где 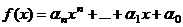 .
.
Если  удовлетворяет сравнению, то оно называется его решением.
удовлетворяет сравнению, то оно называется его решением.
Лемма. Если 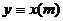 и
и  , то
, то  , то есть всякое число, сравнимое с
, то есть всякое число, сравнимое с 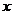 по модулю
по модулю  , тоже является решением сравнения.
, тоже является решением сравнения.
Доказательство.  означает, что
означает, что  .
.
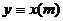

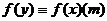 , так как разность
, так как разность  состоит из слагаемых вида
состоит из слагаемых вида 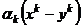 , каждое из которых обязательно делится на
, каждое из которых обязательно делится на 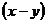 , которое в свою очередь, делится на
, которое в свою очередь, делится на  .
.
Не всякое сравнение разрешимо. Так, при малых  можно проверить непосредственно:
можно проверить непосредственно: 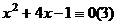 . Переформулируем иначе: Существует ли такое целое
. Переформулируем иначе: Существует ли такое целое 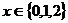 , что
, что  ?
?
Согласно лемме (см. выше), достаточно рассмотреть только 3 числа 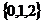 (в общем случае
(в общем случае  ).
).
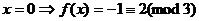 ,
,
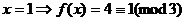 ,
,
 .
.
Рассмотрим сравнения вида  .
.
Теорема 1.
1) Если  , то сравнение
, то сравнение  имеет решение, причём единственное.
имеет решение, причём единственное.
2) Если 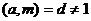 , и
, и 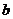 не делится на
не делится на  , то сравнение
, то сравнение  неразрешимо.
неразрешимо.
3) Если 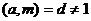 , и
, и  , то сравнение
, то сравнение  имеет
имеет  решений.
решений.
Доказательство.
1) Пусть 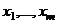 полная система наименьших неотрицательных вычетов по модулю
полная система наименьших неотрицательных вычетов по модулю  , среди них есть одно число, сравнимое с
, среди них есть одно число, сравнимое с 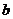 :
:  . Но
. Но  тоже полная система вычетов (теорема 1 см. в прошлом §). Тогда среди них есть ровно одно число, сравнимое с
тоже полная система вычетов (теорема 1 см. в прошлом §). Тогда среди них есть ровно одно число, сравнимое с  из множества
из множества 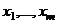 , и тогда
, и тогда  .
.
2) Пусть 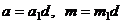 . Тогда
. Тогда  . Пусть сравнение разрешимо, тогда
. Пусть сравнение разрешимо, тогда  , т.е.
, т.е. 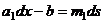

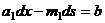

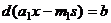

 , противоречие с тем, что
, противоречие с тем, что 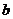 не делится на
не делится на  .
.
Пример.  НОД (a,m)= 5.
НОД (a,m)= 5.
 , неразрешимо: 5x (напр, 5,10,15,20,…) не дают остаток 8 при делении на 10.
, неразрешимо: 5x (напр, 5,10,15,20,…) не дают остаток 8 при делении на 10.
3)  , и при этом
, и при этом  , т.е.
, т.е. 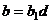 .
.
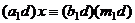



 , сократим на
, сократим на 



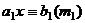 .
.
Здесь уже вынесли НОД, т.е. как в п.1. 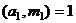 , значит, это сравнение имеет единственное решение,
, значит, это сравнение имеет единственное решение, 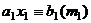 . Оно же является решением и для сравнения
. Оно же является решением и для сравнения  , так как
, так как


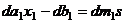 .
.
Перейдём к сравнениям по модулю  . Есть
. Есть  чисел вида
чисел вида  , меньших
, меньших  , они попарно несравнимы по модулю
, они попарно несравнимы по модулю  (все меньше чем
(все меньше чем  ) и тоже являются решениями для
) и тоже являются решениями для  .
.
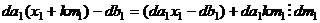 , добавляется величина, содержащая
, добавляется величина, содержащая 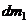 .
.
Что этот п.3 в теореме означает, простыми словами на примере:
Пример. 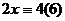 , НОД чисел
, НОД чисел  равен 2, и среди чисел
равен 2, и среди чисел  есть 2 числа, таких что
есть 2 числа, таких что  делится на 6 с остатком 4.
делится на 6 с остатком 4.
Это 2 и 5. Результаты 4 и 10. Пара чисел, т.к. d=2.
ЛЕКЦИЯ 12. 20.3.2021.
Пусть 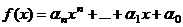 , рассмотрим сравнение
, рассмотрим сравнение  .
.
Если  то b можно перенести влево и вычесть из
то b можно перенести влево и вычесть из 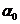 .
.
Теорема 2. Если  - решение сравнения
- решение сравнения  , то это сравнение равносильно
, то это сравнение равносильно  , где
, где  - неполное частное от деления
- неполное частное от деления 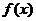 на
на  .
.
Доказательство.
 , где остаток
, где остаток 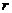 степени, меньшей чем 1, ведь делили на многочлен
степени, меньшей чем 1, ведь делили на многочлен  степени 1. При этом заметим, что
степени 1. При этом заметим, что
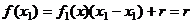 , то есть остаток
, то есть остаток  . По условию,
. По условию,  - это решение сравнения
- это решение сравнения  , то есть
, то есть  .
.
 означает
означает  , где остаток делится на
, где остаток делится на  , значит, и
, значит, и 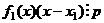 , что и означает
, что и означает  .
.
Следствие. Если  - решения сравнения
- решения сравнения  , то оно равносильно сравнению
, то оно равносильно сравнению  , где
, где  - некоторый многочлен степени
- некоторый многочлен степени 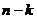 с тем же старшим коэффициентом, который был у
с тем же старшим коэффициентом, который был у 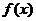 .
.
Теорема 3. Теорема Вильсона.
Число  является простым
является простым 
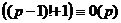 .
.
Доказательство.
Необходимость. Пусть  простое. Тогда по малой теореме Ферма,
простое. Тогда по малой теореме Ферма, 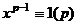 , то есть
, то есть 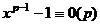 , то есть
, то есть  . Так как есть
. Так как есть  таких чисел
таких чисел 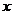 , взаимно простых с
, взаимно простых с  , то сравнение
, то сравнение 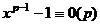 имеет
имеет  решений:
решений:  .
.
Значит, 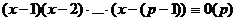 .
.
Кроме того, было 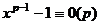 .
.
Рассмотрим разность:  .
.
Если раскрыть скобки, получим многочлен степени меньшей, чем  , и оно имеет
, и оно имеет  решений. Это может быть, только если все коэффициенты делятся на
решений. Это может быть, только если все коэффициенты делятся на  , в частности свободный член уравнения, равный
, в частности свободный член уравнения, равный  =
= 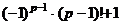 . Однако среди простых чисел, больших 2, нет чётных, так что
. Однако среди простых чисел, больших 2, нет чётных, так что  нечётное, а
нечётное, а  чётное, поэтому
чётное, поэтому 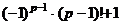 =
= 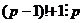 .
.
Отдельно рассмотрим при 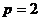 , в том случае вид такой:
, в том случае вид такой:
 , что очевидно и так 0. Впрочем,
, что очевидно и так 0. Впрочем, 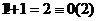 .
.
Достаточность.
Пусть для числа  верно
верно 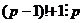 ,и пусть оно не простое,
,и пусть оно не простое,  , где
, где 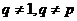 . Тогда
. Тогда 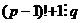 , т.е.
, т.е.  .
.
Но в таком случае 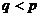 , значит, число
, значит, число  присутствует в факториале:
присутствует в факториале:
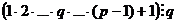 , факториал
, факториал  делится на
делится на  , но тогда должно быть и
, но тогда должно быть и  , что приводит к противоречию, так как 1 не делится на
, что приводит к противоречию, так как 1 не делится на  . Значит, такого числа
. Значит, такого числа  не существует, и
не существует, и  простое.
простое.
Примеры.
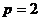


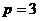
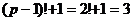

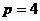
 не делится на 4.
не делится на 4.
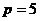
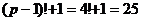

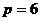
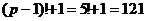 не делится на 6.
не делится на 6.


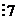 ,
,
здесь вспомним признак делимости: 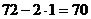
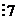 .
.
и так далее.
Теорема 4.
Всякое сравнение 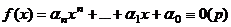 степени
степени  равносильно некоторому сравнению степени не выше
равносильно некоторому сравнению степени не выше  .
.
Доказательство.
По малой теореме Ферма, 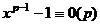 , тогда
, тогда 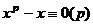 .
.
Поделим многочлен на 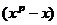 с остатком:
с остатком: 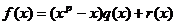 .
.
 делится на
делится на  по условию, первое слагаемое по малой теореме Ферма, значит, остаток
по условию, первое слагаемое по малой теореме Ферма, значит, остаток 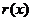 делится на
делится на  . Таким образом, можно перейти к сравнению
. Таким образом, можно перейти к сравнению  , где степень многочлена
, где степень многочлена 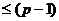 .
.
Определение. Число  называется квадратичным вычетом по модулю
называется квадратичным вычетом по модулю  , если разрешимо сравнение:
, если разрешимо сравнение: 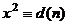 .
.
Теорема 5. Критерий Эйлера.
Число  является квадратичным вычетом по простому нечётному модулю
является квадратичным вычетом по простому нечётному модулю 

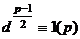 , и не является квадратичным вычетом
, и не является квадратичным вычетом 
 .
.
Доказательство.
Лемма 1. Если  - простое нечётное число, то возможны две ситуации: либо
- простое нечётное число, то возможны две ситуации: либо 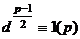 , либо
, либо  .
.
Доказательство. Так как  нечётное, то
нечётное, то  чётное, поэтому
чётное, поэтому 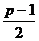 целое. Поделим
целое. Поделим 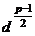 на
на  , и остаток обозначим через
, и остаток обозначим через 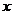 . Так как в этом случае
. Так как в этом случае  , то
, то  , но по малой теореме Ферма
, но по малой теореме Ферма 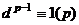 , так что
, так что 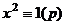 . Это значит,
. Это значит, 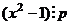 , то есть
, то есть 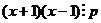 , таким образом,
, таким образом, 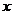 может быть сравнимым только с 1 или
может быть сравнимым только с 1 или 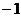 . Напомним, что это был остаток от деления
. Напомним, что это был остаток от деления 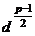 на
на  , так что
, так что 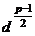 сравнимо только с 1 или
сравнимо только с 1 или 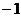 по модулю
по модулю  .
.
Лемма 2. Существует ровно 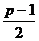 квадратичных вычетов по простому нечётному модулю
квадратичных вычетов по простому нечётному модулю  .
.
Доказательство. Рассмотрим все числа, взаимно простые с  и меньшие чем
и меньшие чем  , это
, это  . Возведём их в квадраты.
. Возведём их в квадраты.
 . Докажем, что
. Докажем, что  .
.
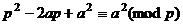 , так как все слагаемые, кроме
, так как все слагаемые, кроме 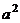 , делятся на
, делятся на  . В таком случае, среди
. В таком случае, среди  квадратов вторая половина даёт те же самые остатки, что и первая (симметрично, см. пример ниже), и существует не более чем
квадратов вторая половина даёт те же самые остатки, что и первая (симметрично, см. пример ниже), и существует не более чем 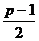 квадратичных вычетов по модулю
квадратичных вычетов по модулю  .
.
Допустим, что их меньше, то есть какие-то из этих вычетов  совпадающие,
совпадающие, 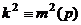 . Но тогда
. Но тогда 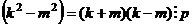 , при этом как сумма, так и разность меньше
, при этом как сумма, так и разность меньше  и делиться на
и делиться на  не может. Сумма, так как оба числа меньше половины
не может. Сумма, так как оба числа меньше половины  , разность тем более. Противоречие, в итоге вывод, что совпадающих среди этих
, разность тем более. Противоречие, в итоге вывод, что совпадающих среди этих 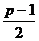 вычетов нет.
вычетов нет.
Пример.  , рассмотрим
, рассмотрим  чисел 1,2,3,4,5,6.
чисел 1,2,3,4,5,6.
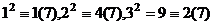 ;
;
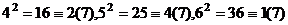 .
.
Вывод: только 1,2,4 могут быть квадратами чего-либо в поле вычетов  . Это 3 числа, что как раз и равно
. Это 3 числа, что как раз и равно 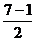 .
.
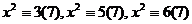 эти 3 сравнения неразрешимы.
эти 3 сравнения неразрешимы.
Итак,
 ;
;  .
.
Рассмотрим теперь все  и установим, какие из них сравнимы с 1, а какие с
и установим, какие из них сравнимы с 1, а какие с 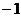 .
.
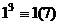
 (
(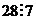 )
)

 (
(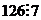 )
)

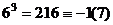 (
(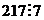 ).
).
Кубы именно тех чисел, которые являются квадратами чего-либо, сравнимы с 1, другие с 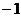 .
.
Доказательство. Теперь докажем критерий Эйлера, с учётом информации из двух лемм. Пусть  является квадратичным вычетом по модулю
является квадратичным вычетом по модулю  , то есть существует
, то есть существует 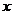 , такое что
, такое что  . В этом случае
. В этом случае 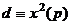 , тогда, возводя в степень
, тогда, возводя в степень 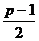 , получим:
, получим:  , а по малой теореме Ферма
, а по малой теореме Ферма 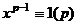 . Следовательно, из-за транзитивности
. Следовательно, из-за транзитивности  .
.
Итак, любой квадратичный вычет является корнем уравнения 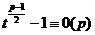 степени
степени 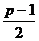 . При этом ранее доказано, что существует
. При этом ранее доказано, что существует 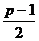 разных квадратичных вычетов. Так как
разных квадратичных вычетов. Так как 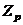 поле, то количество корней не может быть больше cтепени многочлена, и как раз эти
поле, то количество корней не может быть больше cтепени многочлена, и как раз эти 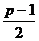 квадратичных вычетов и являются корнями. Оставшиеся
квадратичных вычетов и являются корнями. Оставшиеся 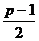 чисел и являются квадратичными невычетами, для них
чисел и являются квадратичными невычетами, для них  .
.



 ,
,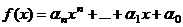 .
.  удовлетворяет сравнению, то оно называется его решением.
удовлетворяет сравнению, то оно называется его решением.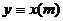 и
и  , то есть всякое число, сравнимое с
, то есть всякое число, сравнимое с 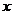 по модулю
по модулю  , тоже является решением сравнения.
, тоже является решением сравнения. .
. 
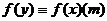 , так как разность
, так как разность  состоит из слагаемых вида
состоит из слагаемых вида 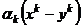 , каждое из которых обязательно делится на
, каждое из которых обязательно делится на 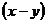 , которое в свою очередь, делится на
, которое в свою очередь, делится на 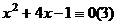 . Переформулируем иначе: Существует ли такое целое
. Переформулируем иначе: Существует ли такое целое 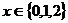 , что
, что  ?
? 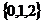 (в общем случае
(в общем случае  ).
). 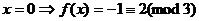 ,
, 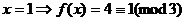 ,
, .
.  .
. , то сравнение
, то сравнение 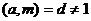 , и
, и 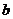 не делится на
не делится на  , то сравнение
, то сравнение  , то сравнение
, то сравнение 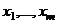 полная система наименьших неотрицательных вычетов по модулю
полная система наименьших неотрицательных вычетов по модулю  . Но
. Но  тоже полная система вычетов (теорема 1 см. в прошлом §). Тогда среди них есть ровно одно число, сравнимое с
тоже полная система вычетов (теорема 1 см. в прошлом §). Тогда среди них есть ровно одно число, сравнимое с  из множества
из множества  .
. 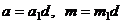 . Тогда
. Тогда  . Пусть сравнение разрешимо, тогда
. Пусть сравнение разрешимо, тогда  , т.е.
, т.е. 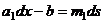
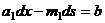
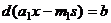
 НОД (a,m)= 5.
НОД (a,m)= 5. , неразрешимо: 5x (напр, 5,10,15,20,…) не дают остаток 8 при делении на 10.
, неразрешимо: 5x (напр, 5,10,15,20,…) не дают остаток 8 при делении на 10.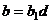 .
. 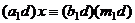

 , сократим на
, сократим на 
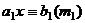 .
. 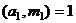 , значит, это сравнение имеет единственное решение,
, значит, это сравнение имеет единственное решение, 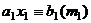 . Оно же является решением и для сравнения
. Оно же является решением и для сравнения 
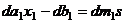 .
.  , меньших
, меньших 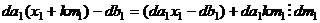 , добавляется величина, содержащая
, добавляется величина, содержащая 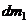 .
. 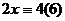 , НОД чисел
, НОД чисел  равен 2, и среди чисел
равен 2, и среди чисел  есть 2 числа, таких что
есть 2 числа, таких что  делится на 6 с остатком 4.
делится на 6 с остатком 4.  .
. то b можно перенести влево и вычесть из
то b можно перенести влево и вычесть из 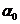 .
. - решение сравнения
- решение сравнения  , где
, где  - неполное частное от деления
- неполное частное от деления 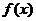 на
на  .
.  , где остаток
, где остаток 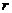 степени, меньшей чем 1, ведь делили на многочлен
степени, меньшей чем 1, ведь делили на многочлен 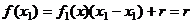 , то есть остаток
, то есть остаток  . По условию,
. По условию,  .
.  , где остаток делится на
, где остаток делится на  , значит, и
, значит, и 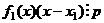 , что и означает
, что и означает  - решения сравнения
- решения сравнения  , где
, где  - некоторый многочлен степени
- некоторый многочлен степени 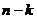 с тем же старшим коэффициентом, который был у
с тем же старшим коэффициентом, который был у 
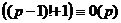 .
. 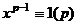 , то есть
, то есть 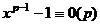 , то есть
, то есть  . Так как есть
. Так как есть  таких чисел
таких чисел  .
. 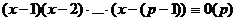 .
. 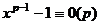 .
. .
. =
= 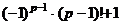 . Однако среди простых чисел, больших 2, нет чётных, так что
. Однако среди простых чисел, больших 2, нет чётных, так что 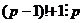 .
. 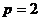 , в том случае вид такой:
, в том случае вид такой: , что очевидно и так 0. Впрочем,
, что очевидно и так 0. Впрочем, 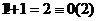 .
. , где
, где 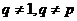 . Тогда
. Тогда 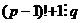 , т.е.
, т.е.  .
. 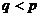 , значит, число
, значит, число  присутствует в факториале:
присутствует в факториале: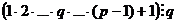 , факториал
, факториал  делится на
делится на  , что приводит к противоречию, так как 1 не делится на
, что приводит к противоречию, так как 1 не делится на 

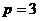
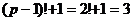

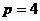
 не делится на 4.
не делится на 4. 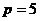
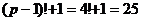

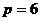
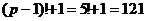 не делится на 6.
не делится на 6. 

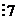 ,
,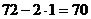
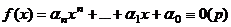 степени
степени  равносильно некоторому сравнению степени не выше
равносильно некоторому сравнению степени не выше 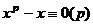 .
.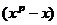 с остатком:
с остатком: 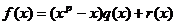 .
. делится на
делится на 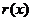 делится на
делится на  , где степень многочлена
, где степень многочлена 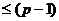 .
.  , если разрешимо сравнение:
, если разрешимо сравнение: 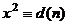 .
. 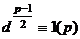 , и не является квадратичным вычетом
, и не является квадратичным вычетом  .
.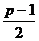 целое. Поделим
целое. Поделим 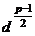 на
на  , то
, то  , но по малой теореме Ферма
, но по малой теореме Ферма 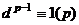 , так что
, так что 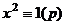 . Это значит,
. Это значит, 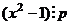 , то есть
, то есть 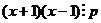 , таким образом,
, таким образом, 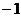 . Напомним, что это был остаток от деления
. Напомним, что это был остаток от деления  . Докажем, что
. Докажем, что  .
.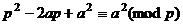 , так как все слагаемые, кроме
, так как все слагаемые, кроме 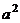 , делятся на
, делятся на  совпадающие,
совпадающие, 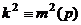 . Но тогда
. Но тогда 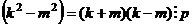 , при этом как сумма, так и разность меньше
, при этом как сумма, так и разность меньше 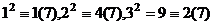 ;
; 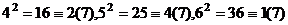 .
.  . Это 3 числа, что как раз и равно
. Это 3 числа, что как раз и равно 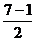 .
.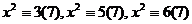 эти 3 сравнения неразрешимы.
эти 3 сравнения неразрешимы. ;
;  .
.  и установим, какие из них сравнимы с 1, а какие с
и установим, какие из них сравнимы с 1, а какие с 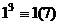
 (
(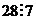 )
)
 (
(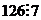 )
)
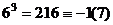 (
(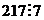 ).
). . В этом случае
. В этом случае 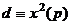 , тогда, возводя в степень
, тогда, возводя в степень  , а по малой теореме Ферма
, а по малой теореме Ферма  .
.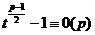 степени
степени 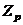 поле, то количество корней не может быть больше cтепени многочлена, и как раз эти
поле, то количество корней не может быть больше cтепени многочлена, и как раз эти 


