Лемма. Если два числа представлены в виде разложений:  ,
, 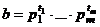 (где некоторые
(где некоторые  или
или 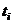 могут быть равны 0, если соответствующего простого числа нет в разложении), то
могут быть равны 0, если соответствующего простого числа нет в разложении), то
НОД (a,b) = 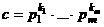 , где
, где  ,
,
НОК (a,b) = 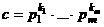 , где
, где  .
.
Лемма. НОД (НОД (a,b),c)= НОД (a,b,c).
Доказательство.
 делит
делит 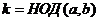 , которое делит
, которое делит  , значит,
, значит,  делит
делит  .
.
Если  не наибольший, и существует
не наибольший, и существует  , на который, в свою очередь делятся все эти числа
, на который, в свою очередь делятся все эти числа 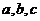 , то
, то  , противоречие.
, противоречие.
Пусть  , тогда
, тогда 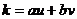 .
.
Пусть  , тогда
, тогда 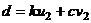 =
= 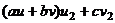 =
=
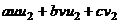 . Итак, если
. Итак, если  , значит, существует разложение
, значит, существует разложение  .
.
Взаимно простые числа: в совокупности и попарно.
Числа  называются взаимно простыми в совокупности, если не существует
называются взаимно простыми в совокупности, если не существует  , которое делит все
, которое делит все  .
.
Числа  называются попарно взаимно простыми, если для каждой пары
называются попарно взаимно простыми, если для каждой пары  , их НОД равен 1.
, их НОД равен 1.
Если числа попарно взаимно просты, то они взаимно просты в совокупности, обратное неверно.
Пример. 6,10,35. 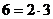
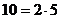
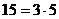
НОД (6,10) = 2, НОД (10,15) = 5, НОД (6,15) = 3.
Общего делителя, на который бы делились все 3 числа, не существует.
НОД (a,b) взаимно прост с c, НОД (a,b,c) = 1.
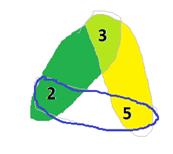
Пересечение каждой пары множеств непусто, а пересечение всех трёх пустое множество.
Лемма. О вынесении общего множителя за знак НОД.
Пусть 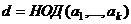 . Тогда
. Тогда  .
.
Доказательство. 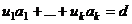

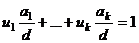 .
.
Теорема. (О взаимосвязи НОД и НОК).
 , т.е.
, т.е.  .
.
Доказательство 1. Разложим a,b в произведение простых множителей, НОК определяется объединением, НОД пересечением. По формуле включений и исключений,  . Когда делим на пересечение, то этим самым исключаем множители, входящие в НОД, ведь в произведении они изначально учитываются по два раза.
. Когда делим на пересечение, то этим самым исключаем множители, входящие в НОД, ведь в произведении они изначально учитываются по два раза.
ЛЕКЦИЯ 10. 13.3.2021.
Доказательство 2. Во-первых,  является общим кратным для
является общим кратным для  :
: 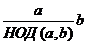 делится на
делится на 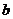 ,
,  делится на
делится на 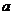 .
.
Покажем теперь, что это именно наименьшее общее кратное. Пусть существует ещё одно кратное, 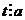 ,
, 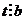 .
.
Тогда 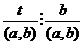 . Пусть
. Пусть  . Тогда
. Тогда  .
.
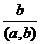 делит левую часть этого равенства, но оно взаимно просто с
делит левую часть этого равенства, но оно взаимно просто с 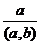 , поэтому делит
, поэтому делит 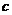 . Тогда
. Тогда  . Тогда
. Тогда 

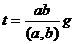 , то есть
, то есть 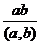 наименьшее общее кратное.
наименьшее общее кратное.
Признаки делимости на 2,3,4,5,6,7,8,9.
Пусть число в десятичной записи имеет вид  , т.е.
, т.е.  .
.
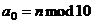 (последняя цифра),
(последняя цифра), 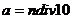 (число, получающееся вычёркиванием последней цифры, т.е.
(число, получающееся вычёркиванием последней цифры, т.е.  ).
).
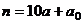 . В этом случае верны признаки делимости на
. В этом случае верны признаки делимости на  (необходимые и достаточные условия):
(необходимые и достаточные условия):

| Условие
|
| 2
|  (последняя цифра 0,2,4,6,8). (последняя цифра 0,2,4,6,8).
|
| 3
| 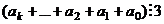
|
| 4
| 
|
| 5
| 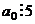 (последняя цифра 0 или 5) (последняя цифра 0 или 5)
|
| 6
|  делится на 2 и 3. делится на 2 и 3.
|
| 7
|  , , 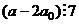 , , 
|
| 8
| 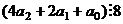
|
| 9
| 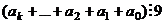
|
Докажем все эти признаки.
Для 2 и 5.
Наиболее просто установить делимость на 2 или 5. Так как 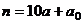 , а
, а  делится на 2 и на 5, то делимость
делится на 2 и на 5, то делимость  на 2 или 5 эквивалентна делимости
на 2 или 5 эквивалентна делимости  на 2 или 5.
на 2 или 5.
Для 3 и 9.
 , вычтем
, вычтем 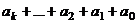 , получится число вида
, получится число вида  , которое делится и на 3, и на 9. Поэтому делимость
, которое делится и на 3, и на 9. Поэтому делимость  на 3 или 9 эквивалентна делимости суммы цифр на то же самое.
на 3 или 9 эквивалентна делимости суммы цифр на то же самое.
n = s + m где s делится на 3, в этом случае делимость n и m экв.
Для 4. Число 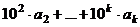 кратно 100, поэтому делится на 4. Разность между ним и
кратно 100, поэтому делится на 4. Разность между ним и  равна
равна  , делимость этого числа на 4 эквивалентна делимости
, делимость этого числа на 4 эквивалентна делимости  на 4.
на 4.
 =
=  , где первая компонента делится на 4, поэтому делимость
, где первая компонента делится на 4, поэтому делимость  на 4 эквивалентна
на 4 эквивалентна  .
.
Для 6. Очевидно, объединение двух свойств делимости, на 2 и 3: последняя цифра чётная и сумма цифр делится на 3.
Для 7.  , где первое слагаемое делится на 7, тогда делимость числа
, где первое слагаемое делится на 7, тогда делимость числа  на 7 эквивалентна
на 7 эквивалентна  .
.
То есть, нужно записать число без последней цифры, утроить его и прибавить  . Мы получаем меньшее число, по которому вывод сделать легче.
. Мы получаем меньшее число, по которому вывод сделать легче.
Но наилучший признак это 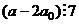 (число без последней цифры, вычесть удвоенную последнюю цифру). Это сильно уменьшает исследуемое число, в 10 раз, причём можно делать несколько шагов, пока не получим какое-нибудь двузначное число, делимость которого на 7 легко выясняется.
(число без последней цифры, вычесть удвоенную последнюю цифру). Это сильно уменьшает исследуемое число, в 10 раз, причём можно делать несколько шагов, пока не получим какое-нибудь двузначное число, делимость которого на 7 легко выясняется.
Докажем его. Рассмотрим  .
.
Так как  , то делимость
, то делимость  эквивалентна делимости
эквивалентна делимости  .
.
При этом  , но так как 10 не делится на 7, то делимость целиком зависит от множителя
, но так как 10 не делится на 7, то делимость целиком зависит от множителя 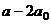 , что и требовалось доказать.
, что и требовалось доказать.
Для доказательства признака  нужно аналогичным образом рассмотреть
нужно аналогичным образом рассмотреть  .
.
Примеры.
Выяснить, делится ли на 7 число  .
.
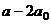 =
= 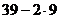 =
=  . 21 делится на 7, поэтому 399 тоже.
. 21 делится на 7, поэтому 399 тоже.
Выяснить, делится ли на 7 число 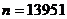 .
.
1) 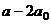 =
= 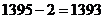 .
.
2) 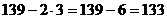 .
.
3)  , делится на 7.
, делится на 7.
Для 8. Так как 1000 делится на 8 (частное 125), то для делимости на 8 достаточно проверять число, состоящее из последних 3 цифр, то есть 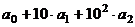 =
=  .
.
 =
=  , где первое слагаемое делится на 8, поэтому делимость на 8 эквивалентна
, где первое слагаемое делится на 8, поэтому делимость на 8 эквивалентна 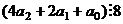 .
.
Остатки и сравнимость по модулю. Вспомним из 1 семестра:
Определение. Два целых числа называются сравнимыми по модулю n, если при делении на n они дают одинаковые остатки, т.е. если их разность делится на n:  . Обозначается
. Обозначается 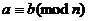 .
.
Таким образом, множество  распадается на n непересекающихся классов.
распадается на n непересекающихся классов. 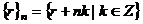 - класс вычетов по модулю n.
- класс вычетов по модулю n.
 означает, что
означает, что  .
.
Свойства сравнимости.
1. 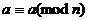 . Рефлексивность
. Рефлексивность
2. 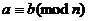

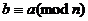 . Симметричность
. Симметричность
3. 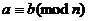 и
и 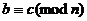

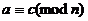 . Транзитивность
. Транзитивность
Свойство 4. 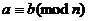 и
и 


Свойство 5. 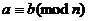 и
и 


(Доказывали в 1 семестре, когда вводили понятие кольца вычетов).
Следствие из свойства 5. 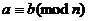

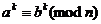 .
.
Пример. 6 и 11, в квадрате 36 и 121, остатки от деления на 5 всё равно 1.



 ,
, 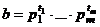 (где некоторые
(где некоторые  или
или 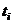 могут быть равны 0, если соответствующего простого числа нет в разложении), то
могут быть равны 0, если соответствующего простого числа нет в разложении), то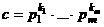 , где
, где  ,
,  .
.  делит
делит 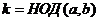 , которое делит
, которое делит  , значит,
, значит,  делит
делит  , на который, в свою очередь делятся все эти числа
, на который, в свою очередь делятся все эти числа 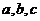 , то
, то  , противоречие.
, противоречие.  , тогда
, тогда 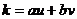 .
.  , тогда
, тогда 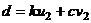 =
= 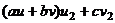 =
=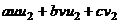 . Итак, если
. Итак, если  , значит, существует разложение
, значит, существует разложение  .
.  называются взаимно простыми в совокупности, если не существует
называются взаимно простыми в совокупности, если не существует  , которое делит все
, которое делит все  , их НОД равен 1.
, их НОД равен 1.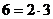
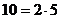
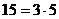

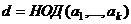 . Тогда
. Тогда  .
.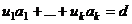

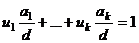 .
. , т.е.
, т.е.  .
. . Когда делим на пересечение, то этим самым исключаем множители, входящие в НОД, ведь в произведении они изначально учитываются по два раза.
. Когда делим на пересечение, то этим самым исключаем множители, входящие в НОД, ведь в произведении они изначально учитываются по два раза. является общим кратным для
является общим кратным для 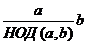 делится на
делится на 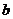 ,
,  делится на
делится на 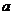 .
. 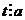 ,
, 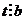 .
.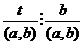 . Пусть
. Пусть  . Тогда
. Тогда  .
. 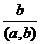 делит левую часть этого равенства, но оно взаимно просто с
делит левую часть этого равенства, но оно взаимно просто с 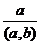 , поэтому делит
, поэтому делит 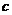 . Тогда
. Тогда  . Тогда
. Тогда 

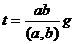 , то есть
, то есть 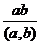 наименьшее общее кратное.
наименьшее общее кратное.  , т.е.
, т.е.  .
.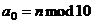 (последняя цифра),
(последняя цифра), 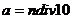 (число, получающееся вычёркиванием последней цифры, т.е.
(число, получающееся вычёркиванием последней цифры, т.е.  ).
).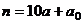 . В этом случае верны признаки делимости на
. В этом случае верны признаки делимости на  (необходимые и достаточные условия):
(необходимые и достаточные условия): (последняя цифра 0,2,4,6,8).
(последняя цифра 0,2,4,6,8).
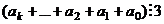

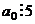 (последняя цифра 0 или 5)
(последняя цифра 0 или 5)
 делится на 2 и 3.
делится на 2 и 3.
 ,
, 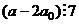 ,
, 
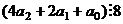
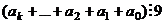
 делится на 2 и на 5, то делимость
делится на 2 и на 5, то делимость  на 2 или 5.
на 2 или 5. 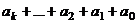 , получится число вида
, получится число вида  , которое делится и на 3, и на 9. Поэтому делимость
, которое делится и на 3, и на 9. Поэтому делимость 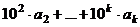 кратно 100, поэтому делится на 4. Разность между ним и
кратно 100, поэтому делится на 4. Разность между ним и  , делимость этого числа на 4 эквивалентна делимости
, делимость этого числа на 4 эквивалентна делимости  , где первая компонента делится на 4, поэтому делимость
, где первая компонента делится на 4, поэтому делимость  , где первое слагаемое делится на 7, тогда делимость числа
, где первое слагаемое делится на 7, тогда делимость числа  .
.  , то делимость
, то делимость  .
.  , но так как 10 не делится на 7, то делимость целиком зависит от множителя
, но так как 10 не делится на 7, то делимость целиком зависит от множителя 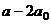 , что и требовалось доказать.
, что и требовалось доказать.  .
. .
. 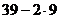 =
=  . 21 делится на 7, поэтому 399 тоже.
. 21 делится на 7, поэтому 399 тоже.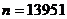 .
. 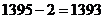 .
.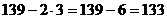 .
. , делится на 7.
, делится на 7.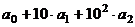 =
=  .
.  =
=  , где первое слагаемое делится на 8, поэтому делимость на 8 эквивалентна
, где первое слагаемое делится на 8, поэтому делимость на 8 эквивалентна  . Обозначается
. Обозначается 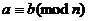 .
.  распадается на n непересекающихся классов.
распадается на n непересекающихся классов. 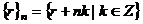 - класс вычетов по модулю n.
- класс вычетов по модулю n.  означает, что
означает, что  .
. 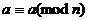 . Рефлексивность
. Рефлексивность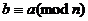 . Симметричность
. Симметричность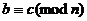
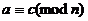 . Транзитивность
. Транзитивность


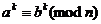 .
. 


