ЛЕКЦИЯ 9. 11.03.2021.
Лемма 6. Всякое натуральное число, большее 1, делится по крайней мере на одно простое число.
Доказательство. Пусть  . Если оно простое, то лемма верна, так как делится на себя (т.е. на простое). Если оно не простое, то оно делится на какое-то другое натуральное число, обозначим его
. Если оно простое, то лемма верна, так как делится на себя (т.е. на простое). Если оно не простое, то оно делится на какое-то другое натуральное число, обозначим его 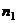 . Если
. Если 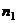 простое, лемма доказана. Если
простое, лемма доказана. Если 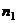 не простое, значит, оно делится на какое-то число
не простое, значит, оно делится на какое-то число  , и т.д.
, и т.д.  поэтому процесс оборвётся через конечное число шагов, и последнее
поэтому процесс оборвётся через конечное число шагов, и последнее  должно быть простым, а не единицей, так как если
должно быть простым, а не единицей, так как если  и
и  не простое, то оно делится на какое-то
не простое, то оно делится на какое-то 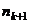 , значит, между
, значит, между  и 1 в этой последовательности было бы ещё какое-то число.
и 1 в этой последовательности было бы ещё какое-то число.
Теорема 7. (Евклид). Каково бы ни было конечное множество простых чисел 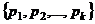 , всегда найдётся простое число, не принадлежащее этому множеству.
, всегда найдётся простое число, не принадлежащее этому множеству.
Доказательство. Рассмотрим число 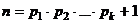 . В силу прошлой леммы, оно делится на некоторое простое число
. В силу прошлой леммы, оно делится на некоторое простое число  . Но это простое число не может совпадать ни с одним из простых чисел
. Но это простое число не может совпадать ни с одним из простых чисел 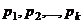 , иначе бы 1 делилась на какое-то
, иначе бы 1 делилась на какое-то  , как разность двух чисел, делящихся на
, как разность двух чисел, делящихся на  . Таким образом, существует какое-то ещё одно простое число, кроме этих, либо само
. Таким образом, существует какое-то ещё одно простое число, кроме этих, либо само 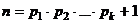 простое.
простое.
Примеры.
 ,
, 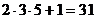 простое.
простое.
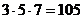 ,
,  , делится на 2, т.е. если
, делится на 2, т.е. если 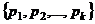 содержит на все по порядку начиная с меньшего, то
содержит на все по порядку начиная с меньшего, то 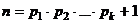 не обязательно простое, но делится на какое-то простое, не входящее в это множество.
не обязательно простое, но делится на какое-то простое, не входящее в это множество.
Предложение 8. Если произведение нескольких целых чисел делится на простое число, то на него делится хотя бы один из сомножителей.
Доказательство.
Докажем методом индукции по числу сомножителей  .
.
1) база индукции. Пусть 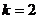 . Пусть
. Пусть 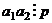 . Если
. Если  , то доказано. Если не делится, то
, то доказано. Если не делится, то  . Тогда по следствию 4,
. Тогда по следствию 4, 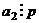 .
.
2) Индукционный шаг. Допустим, что этот факт верен для  сомножителей. Пусть
сомножителей. Пусть  . Рассмотрим
. Рассмотрим  исходных и новый как 2 сомножителя.
исходных и новый как 2 сомножителя.
 . Тогда либо
. Тогда либо  , либо
, либо  . Если последний не делится на
. Если последний не делится на  , то произведение
, то произведение  прочих делится, а для
прочих делится, а для  уже доказано, что если это произведение делится, то хотя бы один из сомножителей делится на
уже доказано, что если это произведение делится, то хотя бы один из сомножителей делится на  .
.
О нахождении НОД и НОК по разложению.
Лемма. Если два числа представлены в виде разложений:  ,
, 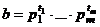 (где некоторые
(где некоторые  или
или 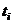 могут быть равны 0, если соответствующего простого числа нет в разложении), то
могут быть равны 0, если соответствующего простого числа нет в разложении), то
НОД (a,b) = 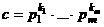 , где
, где  ,
,
НОК (a,b) = 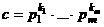 , где
, где  .
.
Лемма. НОД (НОД (a,b),c)= НОД (a,b,c).
Доказательство.
 делит
делит 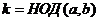 , которое делит
, которое делит  , значит,
, значит,  делит
делит  .
.
Если  не наибольший, и существует
не наибольший, и существует  , на который, в свою очередь делятся все эти числа
, на который, в свою очередь делятся все эти числа 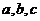 , то
, то  , противоречие.
, противоречие.
Пусть  , тогда
, тогда 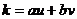 .
.
Пусть  , тогда
, тогда 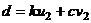 =
= 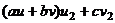 =
=
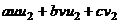 . Итак, если
. Итак, если  , значит, существует разложение
, значит, существует разложение  .
.
ЛЕКЦИЯ 10. 13.3.2021.
Доказательство 2. Во-первых,  является общим кратным для
является общим кратным для  :
: 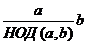 делится на
делится на 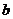 ,
,  делится на
делится на 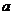 .
.
Покажем теперь, что это именно наименьшее общее кратное. Пусть существует ещё одно кратное, 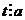 ,
, 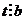 .
.
Тогда 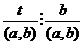 . Пусть
. Пусть  . Тогда
. Тогда  .
.
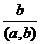 делит левую часть этого равенства, но оно взаимно просто с
делит левую часть этого равенства, но оно взаимно просто с 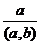 , поэтому делит
, поэтому делит 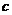 . Тогда
. Тогда  . Тогда
. Тогда 

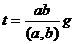 , то есть
, то есть 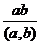 наименьшее общее кратное.
наименьшее общее кратное.
Для 2 и 5.
Наиболее просто установить делимость на 2 или 5. Так как 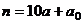 , а
, а  делится на 2 и на 5, то делимость
делится на 2 и на 5, то делимость  на 2 или 5 эквивалентна делимости
на 2 или 5 эквивалентна делимости  на 2 или 5.
на 2 или 5.
Для 3 и 9.
 , вычтем
, вычтем 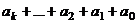 , получится число вида
, получится число вида  , которое делится и на 3, и на 9. Поэтому делимость
, которое делится и на 3, и на 9. Поэтому делимость  на 3 или 9 эквивалентна делимости суммы цифр на то же самое.
на 3 или 9 эквивалентна делимости суммы цифр на то же самое.
n = s + m где s делится на 3, в этом случае делимость n и m экв.
Для 4. Число 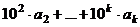 кратно 100, поэтому делится на 4. Разность между ним и
кратно 100, поэтому делится на 4. Разность между ним и  равна
равна  , делимость этого числа на 4 эквивалентна делимости
, делимость этого числа на 4 эквивалентна делимости  на 4.
на 4.
 =
=  , где первая компонента делится на 4, поэтому делимость
, где первая компонента делится на 4, поэтому делимость  на 4 эквивалентна
на 4 эквивалентна  .
.
Для 6. Очевидно, объединение двух свойств делимости, на 2 и 3: последняя цифра чётная и сумма цифр делится на 3.
Для 7.  , где первое слагаемое делится на 7, тогда делимость числа
, где первое слагаемое делится на 7, тогда делимость числа  на 7 эквивалентна
на 7 эквивалентна  .
.
То есть, нужно записать число без последней цифры, утроить его и прибавить  . Мы получаем меньшее число, по которому вывод сделать легче.
. Мы получаем меньшее число, по которому вывод сделать легче.
Но наилучший признак это 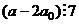 (число без последней цифры, вычесть удвоенную последнюю цифру). Это сильно уменьшает исследуемое число, в 10 раз, причём можно делать несколько шагов, пока не получим какое-нибудь двузначное число, делимость которого на 7 легко выясняется.
(число без последней цифры, вычесть удвоенную последнюю цифру). Это сильно уменьшает исследуемое число, в 10 раз, причём можно делать несколько шагов, пока не получим какое-нибудь двузначное число, делимость которого на 7 легко выясняется.
Докажем его. Рассмотрим  .
.
Так как  , то делимость
, то делимость  эквивалентна делимости
эквивалентна делимости  .
.
При этом  , но так как 10 не делится на 7, то делимость целиком зависит от множителя
, но так как 10 не делится на 7, то делимость целиком зависит от множителя 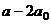 , что и требовалось доказать.
, что и требовалось доказать.
Для доказательства признака  нужно аналогичным образом рассмотреть
нужно аналогичным образом рассмотреть  .
.
Примеры.
Выяснить, делится ли на 7 число  .
.
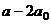 =
= 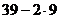 =
=  . 21 делится на 7, поэтому 399 тоже.
. 21 делится на 7, поэтому 399 тоже.
Выяснить, делится ли на 7 число 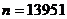 .
.
1) 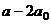 =
= 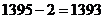 .
.
2) 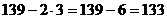 .
.
3)  , делится на 7.
, делится на 7.
Для 8. Так как 1000 делится на 8 (частное 125), то для делимости на 8 достаточно проверять число, состоящее из последних 3 цифр, то есть 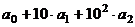 =
=  .
.
 =
=  , где первое слагаемое делится на 8, поэтому делимость на 8 эквивалентна
, где первое слагаемое делится на 8, поэтому делимость на 8 эквивалентна 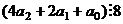 .
.
Остатки и сравнимость по модулю. Вспомним из 1 семестра:
Определение. Два целых числа называются сравнимыми по модулю n, если при делении на n они дают одинаковые остатки, т.е. если их разность делится на n:  . Обозначается
. Обозначается 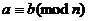 .
.
Таким образом, множество  распадается на n непересекающихся классов.
распадается на n непересекающихся классов. 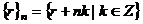 - класс вычетов по модулю n.
- класс вычетов по модулю n.
 означает, что
означает, что  .
.
Свойства сравнимости.
1. 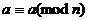 . Рефлексивность
. Рефлексивность
2. 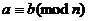

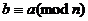 . Симметричность
. Симметричность
3. 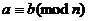 и
и 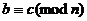

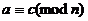 . Транзитивность
. Транзитивность
Свойство 4. 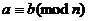 и
и 


Свойство 5. 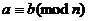 и
и 


(Доказывали в 1 семестре, когда вводили понятие кольца вычетов).
Следствие из свойства 5. 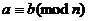

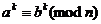 .
.
Пример. 6 и 11, в квадрате 36 и 121, остатки от деления на 5 всё равно 1.
Доказательство.
 =
=
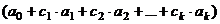 +
+  ,
,
при этом  , то есть
, то есть  . Второе слагаемое делится на
. Второе слагаемое делится на  , тогда остаток от деления первого такой же, как и от деления числа
, тогда остаток от деления первого такой же, как и от деления числа  на
на  .
.
Пример. Выяснить, делится ли 1365 на 13.

 (рассм. 65,78,91,104)
(рассм. 65,78,91,104)
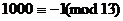 (рассм. 130, 650, 780, 910, 1040, 1001).
(рассм. 130, 650, 780, 910, 1040, 1001).
 =
= 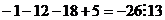 ,
,
проверка:  .
.
* Совершенные числа (ознакомительно).
Число называется совершенным, если оно равно сумме всех своих собственных делителей. Например, 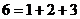 ,
,  .
.
Следующие числа 496, 8128,
До сих пор неизвестно, есть ли нечётные совершенные числа.
Если совершенное число чётно, то оно имеет вид 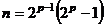 , где
, где  простое.
простое.
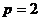 ,
, 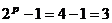 ,
,  .
.
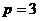 ,
,  ,
, 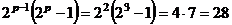 .
.
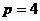 ,
, 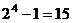 , не простое.
, не простое.
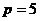 ,
,  ,
,  .
.
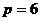 ,
,  не простое.
не простое.
 ,
,  .
.  .
.
ЛЕКЦИЯ 11. 18.3.2021.
Теорема 1. Если  ,
,  - полная система вычетов по модулю
- полная система вычетов по модулю  , то числа вида
, то числа вида  тоже есть полная система вычетов по модулю
тоже есть полная система вычетов по модулю  .
.
(При линейном преобразовании ax+b числа из разных классов вычетов не попадут в один класс, если a взаимно прост с m).
Доказательство.
Докажем, что если  в различных классах вычетов, то
в различных классах вычетов, то 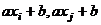 тоже. Если
тоже. Если 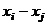 не делится на
не делится на  , то
, то
 =
= 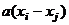 тоже не делится, так как
тоже не делится, так как  .
.
Обозначим 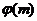 - число вычетов, взаимно простых с
- число вычетов, взаимно простых с  , получится так наз. «приведённая система вычетов».
, получится так наз. «приведённая система вычетов».
Функция Эйлера. 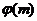 - количество натуральных чисел, не превышающих
- количество натуральных чисел, не превышающих  и взаимно простых с
и взаимно простых с  .
.
Для простого числа  ,
,  , так как множество чисел, с которыми НОД равен 1, это следующее множество:
, так как множество чисел, с которыми НОД равен 1, это следующее множество: 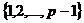 .
.
Теорема 2. Если  ,
, 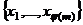 - приведённая система вычетов по модулю
- приведённая система вычетов по модулю  , то
, то  тоже образуют приведённую систему вычетов по модулю
тоже образуют приведённую систему вычетов по модулю  .
.
Доказательство. Если допустить что  то
то
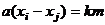 , но
, но 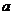 не делится на
не делится на  , значит
, значит  , противоречие, ведь тогда
, противоречие, ведь тогда 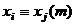 , а это была приведённая система вычетов.
, а это была приведённая система вычетов.
Пример.
1,3,5,7 взаимно просты с  . Умножим на
. Умножим на  .
.
Получим 3,9,15,21. Исследуем остатки при делении на 8.
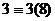 ,
,  ,
, 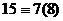 ,
,  .
.
Множество остатков получилось то же самое: 1,3,5,7, но в другом порядке.
Если умножить на 2, не взаимно простое с 8:
2,6,10,14. Остатки: 2,6,2,6 есть повторы, т.к. нарушено условие  .
.
Пример.
1,2,3,4,5,6 взаимно просты с 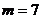 . Возьмём
. Возьмём  . Умножим:
. Умножим:
Получим 5,10,15,20,25,30. Исследуем множество остатков:
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
(как перестановка (5,3,1,6,4,2)).
Теорема 3. Теорема Эйлера. 

 .
.
Доказательство. Пусть 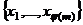 - приведённая система вычетов по модулю
- приведённая система вычетов по модулю  , тогда
, тогда  тоже образуют приведённую систему вычетов по модулю
тоже образуют приведённую систему вычетов по модулю  . Тогда существует какая-то перестановка
. Тогда существует какая-то перестановка  , такая, что:
, такая, что:
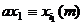 ,
,  ,...,
,..., 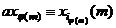 .
.
Сравнения можно умножать (было свойство), тогда
 , где в больших скобках одно и то же число, отличается лишь порядок множителей.
, где в больших скобках одно и то же число, отличается лишь порядок множителей.
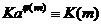

 .
.
Пример. Найти остаток от деления 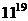 на 7.
на 7.
Заметим, что 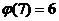 , тогда
, тогда  , и
, и 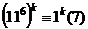 , т.е.
, т.е.  .
.
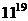 =
= 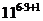 =
= 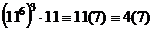 , тогда
, тогда  .
.
Ответ: остаток равен 4, а число 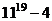 делится на 7.
делится на 7.
Аналогично,  ,
, 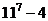 тоже делятся на 7.
тоже делятся на 7.
Теорема 4 (малая теорема Ферма).
Для любого простого числа  и
и  ,
, 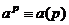 .
.
Доказательство. Пусть  , тогда по теореме Эйлера
, тогда по теореме Эйлера 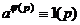 , что означает
, что означает  , тогда
, тогда 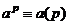 .
.
Пусть  , но
, но  простое, тогда
простое, тогда  , тогда
, тогда  , тогда и
, тогда и 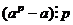 , что и означает
, что и означает 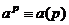 .
.
Замечание. Отличие т.Ферма от теоремы Эйлера:
1) вместо m простое p,
2) число а не должно быть взаимно простым с p.
Мы уже знаем, что  . Теперь рассмотрим, чему равно
. Теперь рассмотрим, чему равно  ,...,
,..., 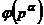 .
.
Лемма.  .
.
Доказательство. Для  : построим квадратную матрицу из чисел:
: построим квадратную матрицу из чисел:

не взаимно просты с  только числа:
только числа:  , это
, это  чисел.
чисел.
Таким образом,  .
.
Для  можно построить не квадратную, а кубическую матрицу, где не взаимно просты с
можно построить не квадратную, а кубическую матрицу, где не взаимно просты с  числа будут только в 2-мерном слое, который состоит из
числа будут только в 2-мерном слое, который состоит из  чисел. Таким образом,
чисел. Таким образом,  .
.
Аналогично,  .
.
Рассмотрим функцию Эйлера произведения двух взаимно простых чисел. Сначала наиболее понятный случай, пусть это будут два простых числа 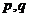 . (Они очевидно, взаимно просты).
. (Они очевидно, взаимно просты).
Лемма. Пусть 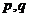 - два простых числа. Тогда
- два простых числа. Тогда  .
.
Доказательство.
Все числа от 1 до 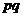 можно записать в виде прямоугольной матрицы:
можно записать в виде прямоугольной матрицы:

из которой видно, что не взаимно простых с 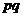 есть всего
есть всего  чисел:
чисел:
 .
.
Если сделать по  элементов в строке, то аналогично получится, что найдём
элементов в строке, то аналогично получится, что найдём  чисел, не взаимно простых с
чисел, не взаимно простых с 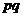 :
:  .
.
В пересечении этих двух множество лишь одно число 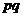 . По формуле включений-исключений, чисел, взаимно простых с
. По формуле включений-исключений, чисел, взаимно простых с 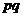 :
:
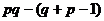 =
=  =
=  .
.
- - - Перерыв - - -
Теорема 5. Функция Эйлера мультипликативна, т.е. если  то
то  .
.
Доказательство (чуть ниже).
Пример. 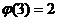 ,
, 

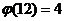 (все чётные и все кратные 3 не взаимно просты с 12, остальные отмечены красным).
(все чётные и все кратные 3 не взаимно просты с 12, остальные отмечены красным).
1 2 3
4 5 6
7 8 9
10 11 12
Доказательство.
Пусть  взаимно простые числа (но не обязательно простые).
взаимно простые числа (но не обязательно простые).
Рассмотрим полную систему вычетов по модулю  :
:
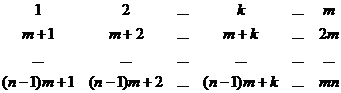
Здесь каждая строка - полная система вычетов по модулю  , а каждый столбец - полная система вычетов по модулю
, а каждый столбец - полная система вычетов по модулю  :
:
 (см. теорему 1).
(см. теорему 1).
Пусть 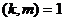 (в первой строке
(в первой строке 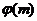 таких чисел). Тогда весь
таких чисел). Тогда весь  -й столбец тоже обладает свойством
-й столбец тоже обладает свойством  , иначе, учитывая
, иначе, учитывая  было бы
было бы 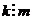 . Итак, есть
. Итак, есть 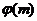 столбцов по
столбцов по  чисел, где все числа взаимно просты с
чисел, где все числа взаимно просты с  . Но каждый столбец представляет собой полную систему вычетов по модулю
. Но каждый столбец представляет собой полную систему вычетов по модулю  , значит, в каждом столбце
, значит, в каждом столбце  чисел, взаимно простых с
чисел, взаимно простых с  . Итак,
. Итак, 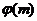 столбцов, где числа взаимно просты с
столбцов, где числа взаимно просты с  , и в каждом по
, и в каждом по  чисел, взаимно простых с
чисел, взаимно простых с  . Итого
. Итого  чисел, взаимно простых с
чисел, взаимно простых с  ,
,  одновременно. Теорема доказана.
одновременно. Теорема доказана.
Примечание. В разных столбцах множество чисел может быть со сдвигом, то есть это не обязательно подматрица из 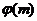 столбцов и
столбцов и  строк. В примере выше показано это (где числа выделены красным).
строк. В примере выше показано это (где числа выделены красным).
Теорема 6. О вычислении функции Эйлера
Пусть 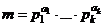 - разложение числа в произведение степеней простых сомножителей, тогда
- разложение числа в произведение степеней простых сомножителей, тогда  .
.
Доказательство.
Пусть 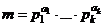 . Из-за мультипликативности функции Эйлера,
. Из-за мультипликативности функции Эйлера,
 . Кроме того, выше мы доказали лемму, что
. Кроме того, выше мы доказали лемму, что  . Тогда
. Тогда  =
= 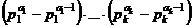 , если вынести за скобку каждое
, если вынести за скобку каждое  , то они как раз и образуют
, то они как раз и образуют 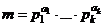 за скобками:
за скобками:
 =
= 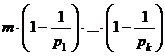 .
.
Пример. Найти количество чисел, не превышающих 36 и взаимно простых с 36.
Решение. 36 = 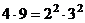 , тогда
, тогда 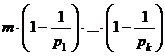 =
=
 =
=  =
=  .
.
Столбцы под чётными должны исключить (2,4,6), и под кратными 3, т.е. 3,6-й. Остаются 2 столбца по 6 чисел, то есть 12 чисел:
1 2 3 4 5 6
7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30
31 32 33 34 35 36
Теорема 1.
1) Если  , то сравнение
, то сравнение  имеет решение, причём единственное.
имеет решение, причём единственное.
2) Если 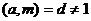 , и
, и 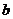 не делится на
не делится на  , то сравнение
, то сравнение  неразрешимо.
неразрешимо.
3) Если 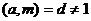 , и
, и  , то сравнение
, то сравнение  имеет
имеет  решений.
решений.
Доказательство.
1) Пусть 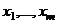 полная система наименьших неотрицательных вычетов по модулю
полная система наименьших неотрицательных вычетов по модулю  , среди них есть одно число, сравнимое с
, среди них есть одно число, сравнимое с 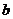 :
:  . Но
. Но  тоже полная система вычетов (теорема 1 см. в прошлом §). Тогда среди них есть ровно одно число, сравнимое с
тоже полная система вычетов (теорема 1 см. в прошлом §). Тогда среди них есть ровно одно число, сравнимое с  из множества
из множества 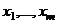 , и тогда
, и тогда  .
.
2) Пусть 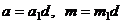 . Тогда
. Тогда  . Пусть сравнение разрешимо, тогда
. Пусть сравнение разрешимо, тогда  , т.е.
, т.е. 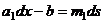

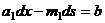

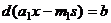

 , противоречие с тем, что
, противоречие с тем, что 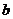 не делится на
не делится на  .
.
Пример.  НОД (a,m)= 5.
НОД (a,m)= 5.
 , неразрешимо: 5x (напр, 5,10,15,20,…) не дают остаток 8 при делении на 10.
, неразрешимо: 5x (напр, 5,10,15,20,…) не дают остаток 8 при делении на 10.
3)  , и при этом
, и при этом  , т.е.
, т.е. 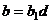 .
.
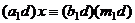



 , сократим на
, сократим на 



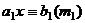 .
.
Здесь уже вынесли НОД, т.е. как в п.1. 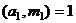 , значит, это сравнение имеет единственное решение,
, значит, это сравнение имеет единственное решение, 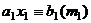 . Оно же является решением и для сравнения
. Оно же является решением и для сравнения  , так как
, так как


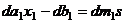 .
.
Перейдём к сравнениям по модулю  . Есть
. Есть  чисел вида
чисел вида  , меньших
, меньших  , они попарно несравнимы по модулю
, они попарно несравнимы по модулю  (все меньше чем
(все меньше чем  ) и тоже являются решениями для
) и тоже являются решениями для  .
.
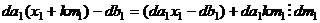 , добавляется величина, содержащая
, добавляется величина, содержащая 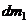 .
.
Что этот п.3 в теореме означает, простыми словами на примере:
Пример. 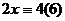 , НОД чисел
, НОД чисел  равен 2, и среди чисел
равен 2, и среди чисел  есть 2 числа, таких что
есть 2 числа, таких что  делится на 6 с остатком 4.
делится на 6 с остатком 4.
Это 2 и 5. Результаты 4 и 10. Пара чисел, т.к. d=2.
ЛЕКЦИЯ 12. 20.3.2021.
Пусть 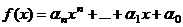 , рассмотрим сравнение
, рассмотрим сравнение  .
.
Если  то b можно перенести влево и вычесть из
то b можно перенести влево и вычесть из 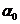 .
.
Теорема 2. Если  - решение сравнения
- решение сравнения  , то это сравнение равносильно
, то это сравнение равносильно  , где
, где  - неполное частное от деления
- неполное частное от деления 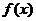 на
на  .
.
Доказательство.
 , где остаток
, где остаток 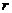 степени, меньшей чем 1, ведь делили на многочлен
степени, меньшей чем 1, ведь делили на многочлен  степени 1. При этом заметим, что
степени 1. При этом заметим, что
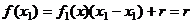 , то есть остаток
, то есть остаток  . По условию,
. По условию,  - это решение сравнения
- это решение сравнения  , то есть
, то есть  .
.
 означает
означает  , где остаток делится на
, где остаток делится на  , значит, и
, значит, и 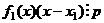 , что и означает
, что и означает  .
.
Следствие. Если  - решения сравнения
- решения сравнения  , то оно равносильно сравнению
, то оно равносильно сравнению  , где
, где  - некоторый многочлен степени
- некоторый многочлен степени 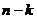 с тем же старшим коэффициентом, который был у
с тем же старшим коэффициентом, который был у 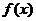 .
.
Доказательство.
Необходимость. Пусть  простое. Тогда по малой теореме Ферма,
простое. Тогда по малой теореме Ферма, 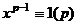 , то есть
, то есть 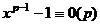 , то есть
, то есть  . Так как есть
. Так как есть  таких чисел
таких чисел 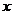 , взаимно простых с
, взаимно простых с  , то сравнение
, то сравнение 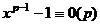 имеет
имеет  решений:
решений:  .
.
Значит, 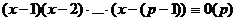 .
.
Кроме того, было 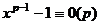 .
.
Рассмотрим разность:  .
.
Если раскрыть скобки, получим многочлен степени меньшей, чем  , и оно имеет
, и оно имеет  решений. Это может быть, только если все коэффициенты делятся на
решений. Это может быть, только если все коэффициенты делятся на  , в частности свободный член уравнения, равный
, в частности свободный член уравнения, равный  =
= 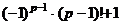 . Однако среди простых чисел, больших 2, нет чётных, так что
. Однако среди простых чисел, больших 2, нет чётных, так что  нечётное, а
нечётное, а  чётное, поэтому
чётное, поэтому 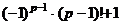 =
= 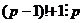 .
.
Отдельно рассмотрим при 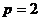 , в том случае вид такой:
, в том случае вид такой:
 , что очевидно и так 0. Впрочем,
, что очевидно и так 0. Впрочем, 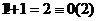 .
.
Достаточность.
Пусть для числа  вер
вер



 . Если оно простое, то лемма верна, так как делится на себя (т.е. на простое). Если оно не простое, то оно делится на какое-то другое натуральное число, обозначим его
. Если оно простое, то лемма верна, так как делится на себя (т.е. на простое). Если оно не простое, то оно делится на какое-то другое натуральное число, обозначим его 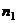 . Если
. Если  , и т.д.
, и т.д.  поэтому процесс оборвётся через конечное число шагов, и последнее
поэтому процесс оборвётся через конечное число шагов, и последнее  должно быть простым, а не единицей, так как если
должно быть простым, а не единицей, так как если  и
и 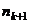 , значит, между
, значит, между 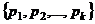 , всегда найдётся простое число, не принадлежащее этому множеству.
, всегда найдётся простое число, не принадлежащее этому множеству.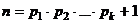 . В силу прошлой леммы, оно делится на некоторое простое число
. В силу прошлой леммы, оно делится на некоторое простое число  . Но это простое число не может совпадать ни с одним из простых чисел
. Но это простое число не может совпадать ни с одним из простых чисел 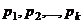 , иначе бы 1 делилась на какое-то
, иначе бы 1 делилась на какое-то  , как разность двух чисел, делящихся на
, как разность двух чисел, делящихся на  ,
, 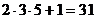 простое.
простое.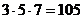 ,
,  , делится на 2, т.е. если
, делится на 2, т.е. если  .
.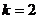 . Пусть
. Пусть 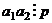 . Если
. Если  , то доказано. Если не делится, то
, то доказано. Если не делится, то  . Тогда по следствию 4,
. Тогда по следствию 4, 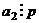 .
.  сомножителей. Пусть
сомножителей. Пусть  . Рассмотрим
. Рассмотрим  . Тогда либо
. Тогда либо  , либо
, либо  . Если последний не делится на
. Если последний не делится на  ,
, 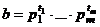 (где некоторые
(где некоторые  или
или 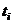 могут быть равны 0, если соответствующего простого числа нет в разложении), то
могут быть равны 0, если соответствующего простого числа нет в разложении), то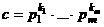 , где
, где  ,
,  .
.  делит
делит 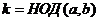 , которое делит
, которое делит  , значит,
, значит,  делит
делит  , на который, в свою очередь делятся все эти числа
, на который, в свою очередь делятся все эти числа 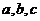 , то
, то  , противоречие.
, противоречие.  , тогда
, тогда 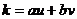 .
.  , тогда
, тогда 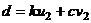 =
= 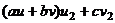 =
=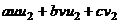 . Итак, если
. Итак, если  , значит, существует разложение
, значит, существует разложение  .
.  является общим кратным для
является общим кратным для 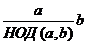 делится на
делится на 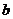 ,
,  делится на
делится на 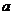 .
. 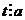 ,
, 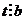 .
.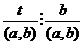 . Пусть
. Пусть  . Тогда
. Тогда  .
. 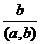 делит левую часть этого равенства, но оно взаимно просто с
делит левую часть этого равенства, но оно взаимно просто с 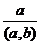 , поэтому делит
, поэтому делит 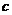 . Тогда
. Тогда  . Тогда
. Тогда 

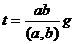 , то есть
, то есть 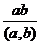 наименьшее общее кратное.
наименьшее общее кратное. 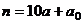 , а
, а  делится на 2 и на 5, то делимость
делится на 2 и на 5, то делимость  на 2 или 5 эквивалентна делимости
на 2 или 5 эквивалентна делимости  на 2 или 5.
на 2 или 5.  , вычтем
, вычтем 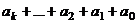 , получится число вида
, получится число вида  , которое делится и на 3, и на 9. Поэтому делимость
, которое делится и на 3, и на 9. Поэтому делимость 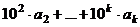 кратно 100, поэтому делится на 4. Разность между ним и
кратно 100, поэтому делится на 4. Разность между ним и  , делимость этого числа на 4 эквивалентна делимости
, делимость этого числа на 4 эквивалентна делимости  , где первая компонента делится на 4, поэтому делимость
, где первая компонента делится на 4, поэтому делимость  .
.  , где первое слагаемое делится на 7, тогда делимость числа
, где первое слагаемое делится на 7, тогда делимость числа  .
. 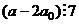 (число без последней цифры, вычесть удвоенную последнюю цифру). Это сильно уменьшает исследуемое число, в 10 раз, причём можно делать несколько шагов, пока не получим какое-нибудь двузначное число, делимость которого на 7 легко выясняется.
(число без последней цифры, вычесть удвоенную последнюю цифру). Это сильно уменьшает исследуемое число, в 10 раз, причём можно делать несколько шагов, пока не получим какое-нибудь двузначное число, делимость которого на 7 легко выясняется.  .
.  , то делимость
, то делимость  .
.  , но так как 10 не делится на 7, то делимость целиком зависит от множителя
, но так как 10 не делится на 7, то делимость целиком зависит от множителя 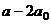 , что и требовалось доказать.
, что и требовалось доказать.  нужно аналогичным образом рассмотреть
нужно аналогичным образом рассмотреть  .
. .
. 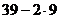 =
=  . 21 делится на 7, поэтому 399 тоже.
. 21 делится на 7, поэтому 399 тоже.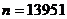 .
. 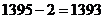 .
.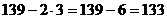 .
. , делится на 7.
, делится на 7.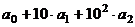 =
=  .
.  =
=  , где первое слагаемое делится на 8, поэтому делимость на 8 эквивалентна
, где первое слагаемое делится на 8, поэтому делимость на 8 эквивалентна 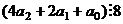 .
. . Обозначается
. Обозначается 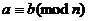 .
.  распадается на n непересекающихся классов.
распадается на n непересекающихся классов. 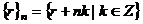 - класс вычетов по модулю n.
- класс вычетов по модулю n.  означает, что
означает, что  .
. 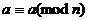 . Рефлексивность
. Рефлексивность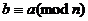 . Симметричность
. Симметричность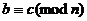
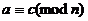 . Транзитивность
. Транзитивность


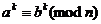 .
. 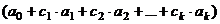 +
+  ,
,  , то есть
, то есть  . Второе слагаемое делится на
. Второе слагаемое делится на  , тогда остаток от деления первого такой же, как и от деления числа
, тогда остаток от деления первого такой же, как и от деления числа 
 (рассм. 65,78,91,104)
(рассм. 65,78,91,104)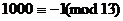 (рассм. 130, 650, 780, 910, 1040, 1001).
(рассм. 130, 650, 780, 910, 1040, 1001).  =
= 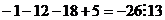 ,
, .
. 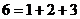 ,
,  .
.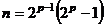 , где
, где  простое.
простое. 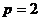 ,
, 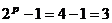 ,
,  .
. 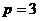 ,
,  ,
, 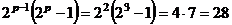 .
. 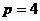 ,
, 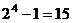 , не простое.
, не простое. 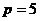 ,
,  ,
,  .
. 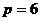 ,
,  не простое.
не простое. ,
,  .
.  .
.  ,
,  - полная система вычетов по модулю
- полная система вычетов по модулю  тоже есть полная система вычетов по модулю
тоже есть полная система вычетов по модулю  в различных классах вычетов, то
в различных классах вычетов, то 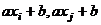 тоже. Если
тоже. Если 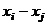 не делится на
не делится на  =
= 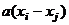 тоже не делится, так как
тоже не делится, так как 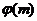 - число вычетов, взаимно простых с
- число вычетов, взаимно простых с  , так как множество чисел, с которыми НОД равен 1, это следующее множество:
, так как множество чисел, с которыми НОД равен 1, это следующее множество: 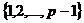 .
. 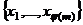 - приведённая система вычетов по модулю
- приведённая система вычетов по модулю  тоже образуют приведённую систему вычетов по модулю
тоже образуют приведённую систему вычетов по модулю  то
то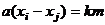 , но
, но  , противоречие, ведь тогда
, противоречие, ведь тогда 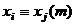 , а это была приведённая система вычетов.
, а это была приведённая система вычетов. . Умножим на
. Умножим на  .
.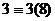 ,
,  ,
, 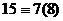 ,
,  .
.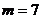 . Возьмём
. Возьмём  . Умножим:
. Умножим: ,
,  ,
,  ,
,  ,
,  ,
,  .
. .
.  , такая, что:
, такая, что: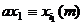 ,
,  ,...,
,..., 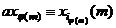 .
.  , где в больших скобках одно и то же число, отличается лишь порядок множителей.
, где в больших скобках одно и то же число, отличается лишь порядок множителей. 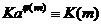
 .
. 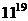 на 7.
на 7. 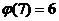 , тогда
, тогда  , и
, и 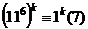 , т.е.
, т.е.  .
. 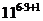 =
= 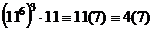 , тогда
, тогда  .
. 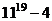 делится на 7.
делится на 7. ,
, 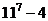 тоже делятся на 7.
тоже делятся на 7. ,
, 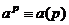 .
.  , тогда по теореме Эйлера
, тогда по теореме Эйлера 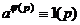 , что означает
, что означает  , тогда
, тогда 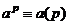 .
. , но
, но  , тогда
, тогда  , тогда и
, тогда и 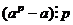 , что и означает
, что и означает  ,...,
,..., 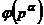 .
.  .
.
 только числа:
только числа:  , это
, это  .
.  можно построить не квадратную, а кубическую матрицу, где не взаимно просты с
можно построить не квадратную, а кубическую матрицу, где не взаимно просты с  .
.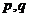 . (Они очевидно, взаимно просты).
. (Они очевидно, взаимно просты). .
. 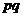 можно записать в виде прямоугольной матрицы:
можно записать в виде прямоугольной матрицы:
 чисел:
чисел: .
.  .
.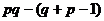 =
=  =
=  .
.  то
то  .
. 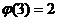 ,
, 
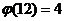 (все чётные и все кратные 3 не взаимно просты с 12, остальные отмечены красным).
(все чётные и все кратные 3 не взаимно просты с 12, остальные отмечены красным).  взаимно простые числа (но не обязательно простые).
взаимно простые числа (но не обязательно простые). :
: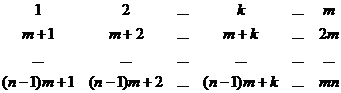
 (см. теорему 1).
(см. теорему 1).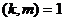 (в первой строке
(в первой строке  , иначе, учитывая
, иначе, учитывая  было бы
было бы 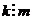 . Итак, есть
. Итак, есть  чисел, взаимно простых с
чисел, взаимно простых с  чисел, взаимно простых с
чисел, взаимно простых с 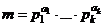 - разложение числа в произведение степеней простых сомножителей, тогда
- разложение числа в произведение степеней простых сомножителей, тогда  .
. . Кроме того, выше мы доказали лемму, что
. Кроме того, выше мы доказали лемму, что 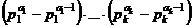 , если вынести за скобку каждое
, если вынести за скобку каждое  , то они как раз и образуют
, то они как раз и образуют  =
= 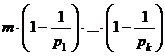 .
. 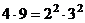 , тогда
, тогда  =
=  =
=  .
.  имеет решение, причём единственное.
имеет решение, причём единственное.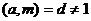 , и
, и  , то сравнение
, то сравнение 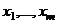 полная система наименьших неотрицательных вычетов по модулю
полная система наименьших неотрицательных вычетов по модулю  . Но
. Но  тоже полная система вычетов (теорема 1 см. в прошлом §). Тогда среди них есть ровно одно число, сравнимое с
тоже полная система вычетов (теорема 1 см. в прошлом §). Тогда среди них есть ровно одно число, сравнимое с  из множества
из множества  .
. 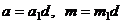 . Тогда
. Тогда  . Пусть сравнение разрешимо, тогда
. Пусть сравнение разрешимо, тогда  , т.е.
, т.е. 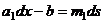
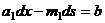
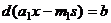
 НОД (a,m)= 5.
НОД (a,m)= 5. , неразрешимо: 5x (напр, 5,10,15,20,…) не дают остаток 8 при делении на 10.
, неразрешимо: 5x (напр, 5,10,15,20,…) не дают остаток 8 при делении на 10.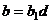 .
. 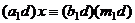

 , сократим на
, сократим на 
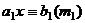 .
. 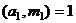 , значит, это сравнение имеет единственное решение,
, значит, это сравнение имеет единственное решение, 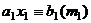 . Оно же является решением и для сравнения
. Оно же является решением и для сравнения 
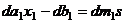 .
.  , меньших
, меньших 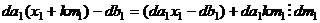 , добавляется величина, содержащая
, добавляется величина, содержащая 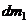 .
. 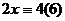 , НОД чисел
, НОД чисел  равен 2, и среди чисел
равен 2, и среди чисел  есть 2 числа, таких что
есть 2 числа, таких что  делится на 6 с остатком 4.
делится на 6 с остатком 4. 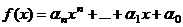 , рассмотрим сравнение
, рассмотрим сравнение  .
. то b можно перенести влево и вычесть из
то b можно перенести влево и вычесть из 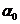 .
. - решение сравнения
- решение сравнения  , где
, где  - неполное частное от деления
- неполное частное от деления 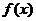 на
на  .
.  , где остаток
, где остаток 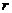 степени, меньшей чем 1, ведь делили на многочлен
степени, меньшей чем 1, ведь делили на многочлен 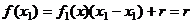 , то есть остаток
, то есть остаток  . По условию,
. По условию,  .
.  , где остаток делится на
, где остаток делится на 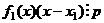 , что и означает
, что и означает  - решения сравнения
- решения сравнения  , где
, где  - некоторый многочлен степени
- некоторый многочлен степени 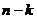 с тем же старшим коэффициентом, который был у
с тем же старшим коэффициентом, который был у 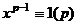 , то есть
, то есть 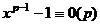 , то есть
, то есть  . Так как есть
. Так как есть  таких чисел
таких чисел 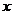 , взаимно простых с
, взаимно простых с  .
. 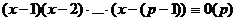 .
. 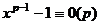 .
. .
. =
= 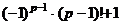 . Однако среди простых чисел, больших 2, нет чётных, так что
. Однако среди простых чисел, больших 2, нет чётных, так что 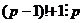 .
.  , что очевидно и так 0. Впрочем,
, что очевидно и так 0. Впрочем, 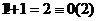 .
.


