1. Ввести новую переменную 
2. Подставить данную переменную в исходное уравнение
3. Решить квадратное уравнение относительно новой переменной
4. После нахождения корней ( ) подставить их в нашу переменную
) подставить их в нашу переменную  и найти исходные корни биквадратного уравнения
и найти исходные корни биквадратного уравнения
Пример решения
Решим биквадратное уравнение  . Сначала приводим это уравнение к квадратному. Для этого введем вспомогательное неизвестное
. Сначала приводим это уравнение к квадратному. Для этого введем вспомогательное неизвестное  такое, что
такое, что  . Тогда
. Тогда  . Теперь данное биквадратное уравнение приводится к виду:
. Теперь данное биквадратное уравнение приводится к виду:
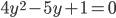
Решая это квадратное уравнение, мы получим 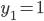 ,
, 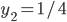 . Так как
. Так как  , то данное биквадратное уравнение эквивалентно системе двух уравнений:
, то данное биквадратное уравнение эквивалентно системе двух уравнений:
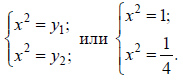
Решим каждое из этих уравнений и найдем объединение множеств их решений.
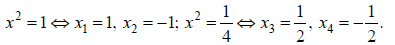
Ответ: 
Понятие корня степени N. Понятие арифметического корня степени N. Понятие степени с рациональным показателем.
Понятие корня степени N
Корнем степени n из действительного числа a, где n - натуральное число, называется такое действительное число x, n -ая степень которого равна a.
Корень степени n из числа a обозначается символом 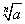 . Согласно этому определению
. Согласно этому определению  .
.
Нахождение корня n -ой степени из числа a называется извлечением корня. Число а называется подкоренным числом (выражением), n - показателем корня. При нечетном n существует корень n -ой степени для любого действительного числа a. При четном n существует корень n -ой степени только для неотрицательного числа a. Чтобы устранить двузначность корня n -ой степени из числа a, вводится понятие арифметического корня n -ой степени из числа a.
Понятие арифметического корня степени N
Если  и n - натуральное число, большее 1, то существует, и только одно, неотрицательное число х, такое, что выполняется равенство
и n - натуральное число, большее 1, то существует, и только одно, неотрицательное число х, такое, что выполняется равенство 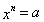 . Это число х называется арифметическим корнем n -й степени из неотрицательного числа а и обозначается
. Это число х называется арифметическим корнем n -й степени из неотрицательного числа а и обозначается 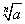 . Число а называется подкоренным числом, n - показателем корня.
. Число а называется подкоренным числом, n - показателем корня.
Итак, согласно определению запись  , где
, где  , означает, во-первых, что
, означает, во-первых, что 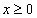 и, во-вторых, что
и, во-вторых, что 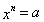 , т.е.
, т.е. 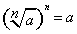 .
.
Поятие степени с рациональным показателем
Степень с натуральным показателем: пусть а - действительное число, а n - натуральное число, большее единицы, n -й степенью числа а называют произведение n множителей, каждый из которых равен а, т.е.  . Число а - основание степени, n - показатель степени. Степень с нулевым показателем: полагают по определению, если
. Число а - основание степени, n - показатель степени. Степень с нулевым показателем: полагают по определению, если  , то
, то 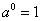 . Нулевая степень числа 0 не имеет смысла. Степень с отрицательным целым показателем: полагают по определению, если
. Нулевая степень числа 0 не имеет смысла. Степень с отрицательным целым показателем: полагают по определению, если  и n - натуральное число, то
и n - натуральное число, то 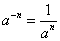 . Степень с дробным показателем: полагают по определению, если
. Степень с дробным показателем: полагают по определению, если  и n - натуральное число, m - целое число, то
и n - натуральное число, m - целое число, то 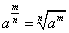 .
.
См. также Свойства степеней
См. также Таблица степеней
Основные свойства степеней
"Свойства степеней" - довольно популярный запрос в поисковых системах, что показывает большой интерес к свойствам степени. Мы собрали для вас все свойства степени (свойства степени с натуральным показателем, свойства степени с рациональным показателем, свойства степени с целым показателем) в одном месте. Вы можете скачать краткую версию шпаргалки "Свойства степеней" в формате.pdf, чтобы при необходимости легко их вспомнить, или ознакомиться со свойствами степеней прямо на сайте. Более подробно свойства степеней с примерами рассмотрены ниже.
Скачать шпаргалку "Свойства степеней" (формат.pdf)
Свойства степеней (кратко)
1. a0=1, если a≠0
2. a1=a
3. (−a)n=an, если n - четное
4. (−a)n=−an, если n - нечетное
5. (a⋅b)n=an⋅bn
6. (ab)n=anbn
7. a−n=1an
8. (ab)−n=(ba)n
9. an⋅am=an+m
10. anam=an−m
11. (an)m=an⋅m
Свойства степеней (с примерами)
1-е свойство степени
Любое число отличное от нуля в нулевой степени равно единице.
a0=1, если a≠0
Например: 1120=1, (−4)0=1, (0,15)0=1
2-е свойство степени
Любое число в первой степени равно самому числу.
a1=a
Например: 231=23, (−9,3)1=−9,3
3-е свойство степени
Любое число в четной степени положительно.
an=an, если n - четное (делящееся на 2) целое число
(−a)n=an, если n - четное (делящееся на 2) целое число
Например: 24=16, (−3)2=32=9, (−1)10=110=1
4-е свойство степени
Любое число в нечетной степени сохраняет свой знак.
an=an, если n - нечетное (не делящееся на 2) целое число
(−a)n=−an, если n - нечетное (не делящееся на 2) целое число
Например: 53=125, (−3)3=−33=−27, (−1)11=−111=−1
5-е свойство степени
Произведение чисел, возведенн ое в степень, можно представить как произведение чисел возведенн ых в эту степень (и наоборот).
(a⋅b)n=an⋅bn, при этом a, b, n - любые допустимые (не обязательно целые) числа
Например: (2,1⋅0,3)4,5=2,14,5⋅0,34,5
6-е свойство степени
Частное (деление) чисел, возведенн ое в степень, можно представить как частное чисел возведенн ых в эту степень (и наоборот).
(ab)n=anbn, при этом a, b, n - любые допустимые (не обязательно целые) числа
Например: (1,75)0,1=(1,7)0,150,1
7-е свойство степени
Любое число в отрицательной степени равно обратному числу в этой степени. (Обратное число это число на которое нужно умножить данное число, чтобы получить единицу.)
a−n=1an, при этом a и n - любые допустимые (не обязательно целые) числа
Например: 7−2=172=149
8-е свойство степени
Любая дробь в отрицательной степени равна обратной дроби в этой степени.
(ab)−n=(ba)n, при этом a, b, n - любые допустимые (не обязательно целые) числа
Например: (23)−2=(32)2, (14)−3=(41)3=43=64
9-е свойство степени
При умножении степеней с одинаковым основанием показатели степени складываются, а основание остается прежним.
an⋅am=an+m, при этом a, n, m - любые допустимые (не обязательно целые) числа
Например: 23⋅25=23+5=28, обратите внимание, что это свойство степени сохраняется и для отрицательных значений степеней 3−2⋅36=3−2+6=34, 47⋅4−3=47+(−3)=47−3=44
10-е свойство степени
При делении степеней с одинаковым основанием показатели степени вычитаются, а основание остается прежним.
anam=an−m, при этом a, n, m - любые допустимые (не обязательно целые) числа
Например: (1,4)2(1,4)3=1,42−3=1,4−1, обратите внимание, как применяется это свойство степени к отрицательным значения степеней3−236=3−2−6=3−8, 474−3=47−(−3)=47+3=410
11-е свойство степени
При возведении степени в степень степени перемножаются.
(an)m=an⋅m
Например: (23)2=23⋅2=26=64
Аблица степеней до 10
Мало кому удается запомнить всю таблицу степеней, да и кому это нужно когда ее так легко найти? Наша таблица степеней включает в себя как популярные таблицы квадратов и кубов (от 1 до 10), так и таблицы других степеней, которые встречаются реже. В столбцах таблицы степеней указываются основания степени (число, которое нужно возвести в степень), в строках – показатели степени (степень, в которую нужно возвести число), на пересечении нужного столбца и нужной строки находится результат возведения нужного числа в заданную степень. Существуют несколько типов задач, решаемых с помощью таблицы степеней. Прямая задача – это вычислить n -ю степень числа. Обратная задача, которая так же может быть решена с помощью таблицы степеней, может звучать так: "в какую степень нужно возвести число a, чтобы получить число b?" или "Какое число в степени n дает число b?".
Таблица степеней до 10
|
| 1 n
| 2 n
| 3 n
| 4 n
| 5 n
| 6 n
| 7 n
| 8 n
| 9 n
| 10 n
|
| 1
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
|
| 2
| 1
| 4
| 9
| 16
| 25
| 36
| 49
| 64
| 81
| 100
|
| 3
| 1
| 8
| 27
| 64
| 125
| 216
| 343
| 512
| 729
| 1000
|
| 4
| 1
| 16
| 81
| 256
| 625
| 1296
| 2401
| 4096
| 6561
| 10000
|
| 5
| 1
| 32
| 243
| 1024
| 3125
| 7776
| 16807
| 32768
| 59049
| 100000
|
| 6
| 1
| 64
| 729
| 4096
| 15625
| 46656
| 117649
| 262144
| 531441
| 1000000
|
| 7
| 1
| 128
| 2187
| 16384
| 78125
| 279936
| 823543
| 2097152
| 4782969
| 10000000
|
| 8
| 1
| 256
| 6561
| 65536
| 390625
| 1679616
| 5764801
| 16777216
| 43046721
| 100000000
|
| 9
| 1
| 512
| 19683
| 262144
| 1953125
| 10077696
| 40353607
| 134217728
| 387420489
| 1000000000
|
| 10
| 1
| 1024
| 59049
| 1048576
| 9765625
| 60466176
| 282475249
| 1073741824
| 3486784401
| 10000000000
|




 ) подставить их в нашу переменную
) подставить их в нашу переменную  . Сначала приводим это уравнение к квадратному. Для этого введем вспомогательное неизвестное
. Сначала приводим это уравнение к квадратному. Для этого введем вспомогательное неизвестное  такое, что
такое, что  . Теперь данное биквадратное уравнение приводится к виду:
. Теперь данное биквадратное уравнение приводится к виду: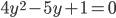
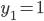 ,
, 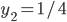 . Так как
. Так как 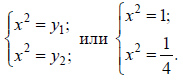
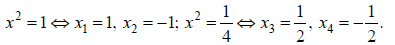

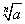 . Согласно этому определению
. Согласно этому определению  .
. и n - натуральное число, большее 1, то существует, и только одно, неотрицательное число х, такое, что выполняется равенство
и n - натуральное число, большее 1, то существует, и только одно, неотрицательное число х, такое, что выполняется равенство 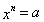 . Это число х называется арифметическим корнем n -й степени из неотрицательного числа а и обозначается
. Это число х называется арифметическим корнем n -й степени из неотрицательного числа а и обозначается  , где
, где 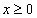 и, во-вторых, что
и, во-вторых, что 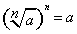 .
. . Число а - основание степени, n - показатель степени. Степень с нулевым показателем: полагают по определению, если
. Число а - основание степени, n - показатель степени. Степень с нулевым показателем: полагают по определению, если  , то
, то 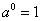 . Нулевая степень числа 0 не имеет смысла. Степень с отрицательным целым показателем: полагают по определению, если
. Нулевая степень числа 0 не имеет смысла. Степень с отрицательным целым показателем: полагают по определению, если 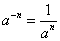 . Степень с дробным показателем: полагают по определению, если
. Степень с дробным показателем: полагают по определению, если  и n - натуральное число, m - целое число, то
и n - натуральное число, m - целое число, то 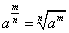 .
.


