

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
 Если
Если  непрерывна в точке а, то она ограничена в некоторой окрестности точки а, т. е.
непрерывна в точке а, то она ограничена в некоторой окрестности точки а, т. е.  и
и 
 .
.
 Если
Если  непрерывна в точке а, причем
непрерывна в точке а, причем 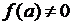 , то существует такая окрестность точки а, в которой знак функции
, то существует такая окрестность точки а, в которой знак функции  совпадает со знаком числа
совпадает со знаком числа  .
.
 Если
Если  и
и 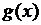 непрерывны в точке а, то функции
непрерывны в точке а, то функции  ,
, 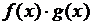 ,
,  (при условии, что
(при условии, что  ) непрерывны в точке а.
) непрерывны в точке а.
 Теорема (непрерывность сложной функции) Если функция
Теорема (непрерывность сложной функции) Если функция  непрерывна в точке
непрерывна в точке  , функция
, функция  непрерывна в точке
непрерывна в точке  , то в некоторой окрестности точки
, то в некоторой окрестности точки  определена сложная функция
определена сложная функция  , которая непрерывна в точке
, которая непрерывна в точке  .
.
Свойства функций, непрерывных на отрезке (глобальные свойства непрерывных функций)
1. Ограниченность непрерывной на отрезке функции.
Теорема 1 (Вейерштрасса) Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она ограничена на нём, т. е.
, то она ограничена на нём, т. е.  .
.
Замечание. Теорема неверна на промежутках, не являющихся отрезками. Например,  непрерывна на
непрерывна на  , но не ограничена на нём; функция
, но не ограничена на нём; функция 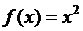 непрерывна на R, но не ограничена на R.
непрерывна на R, но не ограничена на R.
2. Достижение точных граней.
Теорема 2 (Вейерштрасса) Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она достигает своих точной верхней и точной нижней граней, т.е.
, то она достигает своих точной верхней и точной нижней граней, т.е.
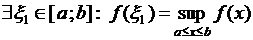 и
и 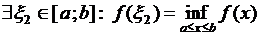
3. Промежуточные значения непрерывной функции.
Теорема (Коши о нулях непрерывной функции)Если функция  непрерывна на отрезке
непрерывна на отрезке  и принимает в его концах значения разных знаков, то существует точка
и принимает в его концах значения разных знаков, то существует точка 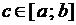 такая, что
такая, что  .
.
Замечание. Теорема Коши о нулях непрерывной функции утверждает, что график непрерывной функции, принимающеё на концах отрезка значения разных знаков, пересекает ось Ox хотя бы в одной точке отрезка  .
.
Теорема (Коши о промежуточных значениях)Если функция  непрерывна на отрезке
непрерывна на отрезке  и
и 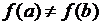 , то для
, то для 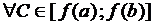 найдется такая точка
найдется такая точка 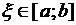 , что
, что  .
.
|
|
Следствие Если функция  непрерывна на отрезке
непрерывна на отрезке  ,
, 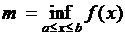 ,
,  , то множество значений, принимаю-щих функцией на отрезке
, то множество значений, принимаю-щих функцией на отрезке  , есть отрезок
, есть отрезок 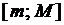 .
.
4. Существование и непрерывность функции, обратной к непрерывной.
Теорема Если функция  непрерывна и строго возрастает на отрезке
непрерывна и строго возрастает на отрезке  , то на отрезке
, то на отрезке  определена функция
определена функция 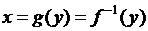 , обратная к
, обратная к  , непрерывная и строго возрастающая.
, непрерывная и строго возрастающая.
Примеры 1) Так как функция 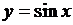 непрерывна и возрастает на
непрерывна и возрастает на  , то на
, то на 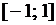 определена обратная функция
определена обратная функция 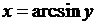 , которая непрерывна на
, которая непрерывна на 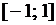 и строго возрастает.
и строго возрастает.
2) функция 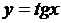 строго возрастает и непрерывна на
строго возрастает и непрерывна на 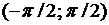 . Значит, на R определена, возрастает и непрерывна обратная функция
. Значит, на R определена, возрастает и непрерывна обратная функция 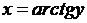 .
.
Производная функции в точке
 5.1 Определение. Физический и геометрический смысл производной
5.1 Определение. Физический и геометрический смысл производной
Пусть  – путь, пройденный материальной точкой за время t. Тогда средняя скорость материальной точки за промежуток
– путь, пройденный материальной точкой за время t. Тогда средняя скорость материальной точки за промежуток  есть величина, равная
есть величина, равная  .
.
Тогда  мгновенная скорость движения материальной точки в момент времени
мгновенная скорость движения материальной точки в момент времени  .
.
Обозначим 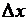 – приращение аргумента х,
– приращение аргумента х,
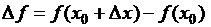 – приращение функции
– приращение функции  , соответ-ствующее приращению
, соответ-ствующее приращению 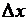 .
.
О. Производной функции в точке  называется число (если оно существует), равное пределу отношения приращения функции в точке
называется число (если оно существует), равное пределу отношения приращения функции в точке  к приращению аргумента при условии, что
к приращению аргумента при условии, что  и обозначается
и обозначается 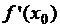 , т. е.
, т. е.  .
.
Механический смысл производной. Если х – время,  – путь, пройденный материальной точкой за время х, то
– путь, пройденный материальной точкой за время х, то 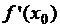 – это скорость движения в момент времени
– это скорость движения в момент времени  или
или 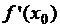 –мгновенная скорость изменения функции
–мгновенная скорость изменения функции  в момент времени
в момент времени  .
.
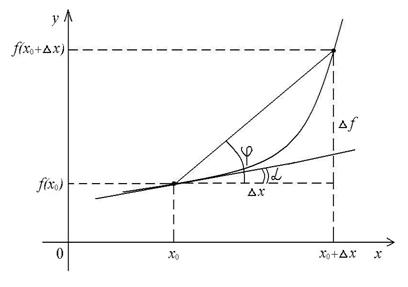
Геометрический смысл производной. 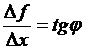 – это тангенс угла наклона секущей, проходящей через точки с координатами
– это тангенс угла наклона секущей, проходящей через точки с координатами  и
и  .
.
При 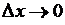
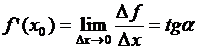 – тангенс угла наклона касательной, проведенной к графику функции
– тангенс угла наклона касательной, проведенной к графику функции  в точке
в точке  .
.
Если  уравнение касательной, то
уравнение касательной, то  .
.
Уравнение касательной: 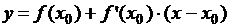 .
.
Примеры 1)  .
.
 , т. е. производная постоянной функции равна 0.
, т. е. производная постоянной функции равна 0.
2) 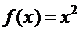 . Покажем, что
. Покажем, что 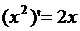 . Действительно,
. Действительно, 
 .
.
3)  .
.

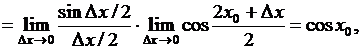 т. е.
т. е.  .
.
Теорема Если  имеет производную в точке
имеет производную в точке  , то
, то  непрерывна в точке
непрерывна в точке  .
.
Замечание. Если  разрывна в точке
разрывна в точке  , то она не имеет производной в точке
, то она не имеет производной в точке  .
.
|
|
По аналогии с односторонними пределами вводятся понятия односторонних производных:
 ,
,  – правосторонняя и левосторонняя производные функции
– правосторонняя и левосторонняя производные функции  в точке
в точке  .
.
Пример  . Найти односторонние производные.
. Найти односторонние производные.
Решение. 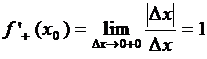 ,
,
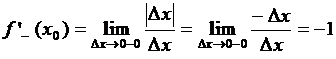 .
.
Так как односторонние производные не равны, то  не имеет производной в точке
не имеет производной в точке  .
.
Дифференциал функции
Пусть функции  определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.
О. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если её приращение в точке
, если её приращение в точке  представимо в виде:
представимо в виде:
 ,
,
где А – постоянная, не зависящая от 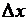 (но зависящая от
(но зависящая от  ), а функция
), а функция 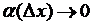 при
при 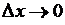 .
.
Слагаемое 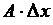 называется дифференциалом функции
называется дифференциалом функции  в точке
в точке  и обозначается
и обозначается  или
или 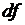 . Дифференциал – это главное линейная часть приращения функции. Тогда
. Дифференциал – это главное линейная часть приращения функции. Тогда  ,
, 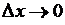 .
.
Теорема Функция  дифференцируема в точке
дифференцируема в точке  тогда, и только тогда, когда она имеет производную в точке
тогда, и только тогда, когда она имеет производную в точке  . При этом
. При этом
 .
.
Обычно 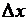 обозначают
обозначают  и пишут
и пишут  .
.
Правила дифференцирования
Теорема 1 Если функции  и
и 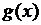 дифференцируемы в точке
дифференцируемы в точке  , то в этой точке дифференцируемы функции
, то в этой точке дифференцируемы функции

 (если
(если 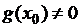 ),
),
причем 1)  ,
,
2)  ,
,
3)  ,
,  .
.
Следствие  , где
, где  .
.
Теорема 3 (дифференцирование сложной функции) Если 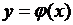 дифференцируема в точке
дифференцируема в точке  ,
,  дифференцируема в точке
дифференцируема в точке  , то сложная функция
, то сложная функция  дифференцируема в точке
дифференцируема в точке 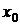 , причем
, причем 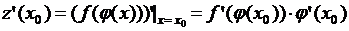 .
.
Таблица производных от основных элементарных функций
1) 
2) 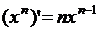 ,
, 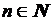 ,
,  ,
, 
3) 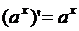 ,
, 
4)  ,
, 
5)  , 6)
, 6) 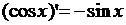
7)  , 8)
, 8) 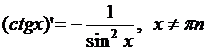

9)  , 10)
, 10) 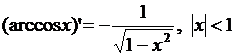
11)  , 12)
, 12) 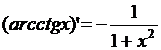
13)  , 14)
, 14) 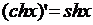
15)  , 16)
, 16) 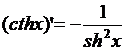
|
|
|

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!