Логическая символика и терминология
Для сокращения записей будем использовать логические символы:
 – принадлежит,
– принадлежит,
 – содержится,
– содержится,
 – любой, для любого, каждый, для всех и т. п.,
– любой, для любого, каждый, для всех и т. п.,
 – существует, найдется,
– существует, найдется,
: или | – заменяет слова «такой, что…»,
! – единственный,
 – знак следования (в записи
– знак следования (в записи  условие А называется достаточным для В, условие В называется необходимым для А),
условие А называется достаточным для В, условие В называется необходимым для А),
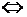 – знак равносильности (означает, что
– знак равносильности (означает, что  и при этом
и при этом  ),
),
■ – знак окончания доказательства.
Точные грани числовых множеств
Пусть  .
.
О. Множество Х называется ограниченным сверху, если
 :
: 
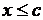 .
.
Число с называется верхней гранью множества Х.
О. Множество Х называется ограниченным снизу, если
 :
: 
 .
.
Число  называется нижней гранью множества Х.
называется нижней гранью множества Х.
О. Множество Х называется ограниченным, если оно ограничено и сверху, и снизу, т.е.  :
: 
 .
.
Утверждение Множество Х ограничено тогда, и только тогда, когда 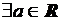 :
: 
 .
.
О. Максимальным элементом множества Х называется такое число а, что 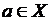 :
: 
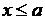 .
.
О. Минимальным элементом множества Х называется такое число а, что 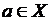 :
: 
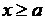 .
.
О. Множество Х называется не ограниченным сверху, если
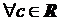 :
:  :
: 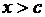 .
.
О. Множество Х называется не ограниченным снизу, если
 :
:  :
: 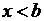 .
.
О. Множество Х называется неограниченным, если оно не ограничено сверху или не ограничено снизу.
О. Точная верхняя грань – это наименьшая из всех верхних граней, т.е.  (супремум), если
(супремум), если
1) 
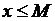 ; 2)
; 2)  .
.
Или  .
.
О. Точная нижняя грань – это наибольшая из всех нижних граней, т.е.  (инфинум), если
(инфинум), если
1) 
 ; 2)
; 2) 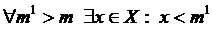 .
.
Или  .
.
Замечание. 1) Множество может не иметь максимального элемента, но иметь точную верхнюю грань. Например, таково множество 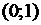 .
.
2) Если существует максимальный элемент множества Х, то он совпадает с 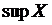 .
.
3) Если множество Х не ограничено сверху, то  , если Х не ограничено снизу, то
, если Х не ограничено снизу, то 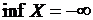 .
.
Теорема о существовании точной верхней грани Если множество Х ограничено сверху, то оно имеет, причем единственную, точную верхнюю грань.
Натуральные, рациональные, иррациональные числа
О. Множество М называется индуктивным, если
 .
.
О. Множество натуральных чисел – это наименьшее индуктивное множество, содержащее 1. Обозначается N  .
.
О. Множество целых чисел – это множество
Z  N
N  .
.
О. Множество рациональных чисел – это множество
Q  целое,
целое,  натуральное
натуральное  .
.
Числа, которые не являются рациональными, называются иррациональными.
Любое рациональное число можно представить в виде конечной или бесконечной периодической десятичной дроби. Например,  . Иррациональное число – это всегда бесконечная непериодическая десятичная дробь.
. Иррациональное число – это всегда бесконечная непериодическая десятичная дробь.
 2 Числовые последовательности
2 Числовые последовательности
Определения
Функцией называется правило (закон), по которому каждому элементу множества Х ставится в соответствие единственный элемент множества Y.
Обозначается  или
или  . Множество Х при этом называется областью определения, а множество Y – областью значений.
. Множество Х при этом называется областью определения, а множество Y – областью значений.
Последовательность – это функция, область определения которой есть множество N всех натуральных чисел.
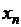 – n -ый член последовательности,
– n -ый член последовательности,  номер члена
номер члена 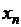 .
.
Примеры  .
.
О. Последовательность называется ограниченной сверху, если
 :
: 
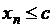 .
.
О. Последовательность называется ограниченной снизу, если
 :
: 
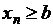 .
.
О. Последовательность называется ограниченной, если
 :
: 
 .
.
О. Последовательность называется возрастающей с номера 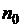 , если
, если 
 .
.
О. Последовательность называется убывающей с номера 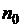 , если
, если

 .
.
Предел последовательности
О. Число а называется пределом последовательности 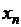 , если
, если
 .
.
Обозначается 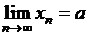 .
.
 окрестностью
окрестностью  точки а называется симметричный интервал
точки а называется симметричный интервал  . Следующие записи равносильны:
. Следующие записи равносильны:
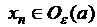
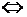
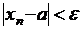
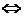
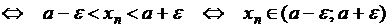 .
.
Это значит, для любой окрестности точки а существует такой номер 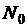 , что все члены последовательности с номерами, большими, чем этот, принадлежат этой окрестности, т.е.
, что все члены последовательности с номерами, большими, чем этот, принадлежат этой окрестности, т.е.
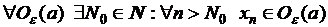 .
.
Пример 1 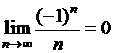 , так как
, так как

(квадратные скобки означают целую часть числа).
Если существует  , то говорят, что последовательность
, то говорят, что последовательность 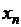 сходится, в противном случае – расходится.
сходится, в противном случае – расходится.
Пример 2 Последовательность 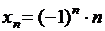 не имеет предела, так как нет такого числа, в окрестности которого находились бы все члены этой последовательности, начиная с некоторого номера.
не имеет предела, так как нет такого числа, в окрестности которого находились бы все члены этой последовательности, начиная с некоторого номера.
Предел функции в точке
Определение предела по Коши
 Напомним, что
Напомним, что 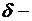 окрестностью точки a называется множество
окрестностью точки a называется множество
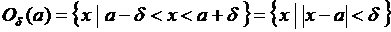 .
.
Если из этого множества удалить точку a, то получим проколотую окрестность 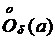 .
.
О. Число А называется пределом функции  в точке a, если
в точке a, если
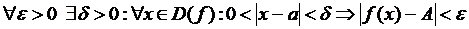 ,
,
то есть для 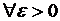 найдется такое
найдется такое 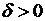 , что для
, что для 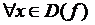 , отличающегося от a меньше, чем на
, отличающегося от a меньше, чем на 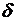 , и не равного a, выполняется неравенство
, и не равного a, выполняется неравенство 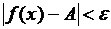 .
.
Пишут 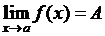 .
.
На языке окрестностей 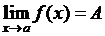 означает, что
означает, что
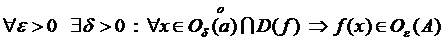 .
.
Пример 1 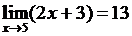
Решение. Здесь 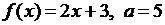 . Нужно доказать, что
. Нужно доказать, что
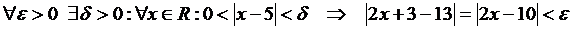 .
.
Действительно, 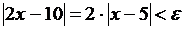 , если
, если 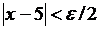 . Т. о.,
. Т. о.,
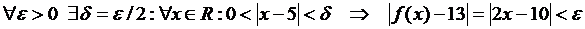 .
.
Пример 2 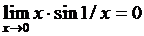
Решение. 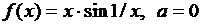 ,
, 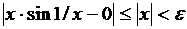 , если взять
, если взять 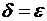 .
.
Значит, 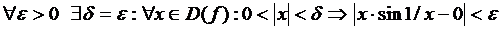 .
.
Теорема Если функция  имеет предел в точке a, то он − единственный.
имеет предел в точке a, то он − единственный.
Доказательство. Допустим, 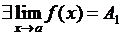 и
и 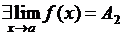 , причем для определенности будем считать, что
, причем для определенности будем считать, что 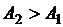 .
.
Возьмем непересекающиеся окрестности точек 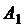 и
и 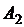 . Так как
. Так как 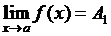 , то для
, то для 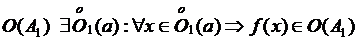 . Т. к.
. Т. к.  , то для
, то для 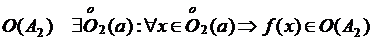 .
.
Рассмотрим 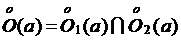 . Тогда
. Тогда 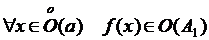 и
и 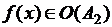 . Противоречие. ■
. Противоречие. ■
Различные типы пределов
а) Односторонние пределы.
О. Число 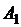 называется пределом слева функции
называется пределом слева функции  в точке a и обозначается
в точке a и обозначается 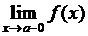 , если
, если
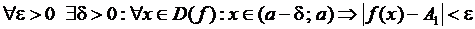 .
.
Аналогично 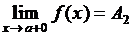 означает, что
означает, что
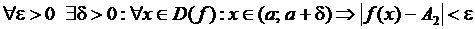 .
.
Пределы слева и справа называются односторонними.
Обозначаются также 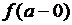 и
и 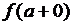 .
.
б) Бесконечные пределы в конечной точке.
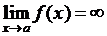 , если
, если 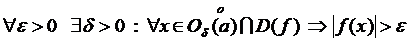 .
.
Например, 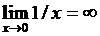 .
.
в) Предел в бесконечности.
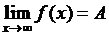 , если
, если 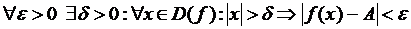 .
.
Например, 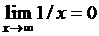 .
.
Предел монотонной функции
О. Функция называется возрастающей на множестве Х, если
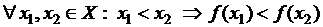 .
.
О. Функция называется неубывающей на множестве Х, если
 .
.
О. Функция называется убывающей на множестве Х, если
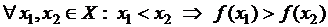 .
.
О. Функция называется невозрастающей на множестве Х, если
 .
.
Теорема 1 Для того, чтобы неубывающая функция 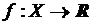 имела предел при
имела предел при  или
или  , необходимо и достаточно, чтобы функция
, необходимо и достаточно, чтобы функция 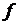 была ограничена на Х сверху.
была ограничена на Х сверху.
Теорема 2 Для того, чтобы невозрастающая функция 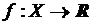 имела предел при
имела предел при 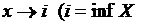 или
или  , необходимо и достаточно, чтобы функция
, необходимо и достаточно, чтобы функция 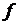 была ограничена на Х снизу.
была ограничена на Х снизу.
Бесконечно малые функции
О. Если  , то функцию
, то функцию 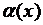 называют бесконечно малой при
называют бесконечно малой при 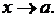
Свойства бесконечно малых функций
1) Сумма конечного числа б.м. функций при 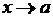 есть б.м. функция при
есть б.м. функция при 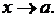
2) Произведение б.м. функции на ограниченную в некоторой проколотой окрестности точки a функцию есть б.м. функция при 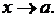
3) Произведение конечного числа б.м. функций при 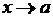 есть б.м. функция при
есть б.м. функция при 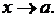
Первый замечательный предел
Теорема 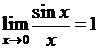 .
.
Второй замечательный предел
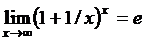
Сделав в последнем пределе замену  , получим
, получим
 .
.
Утверждение Если 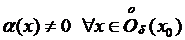 и
и 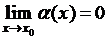 , то
, то
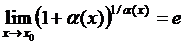 .
.
Пример 1  .
.
Пример 2 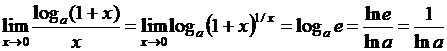 .
.
В последнем примере при  получим
получим 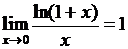 .
.
 4 Непрерывные функции
4 Непрерывные функции
Определение
О. Функция  называется непрерывной в точке а, если она определена в некоторой окрестности этой точки и
называется непрерывной в точке а, если она определена в некоторой окрестности этой точки и 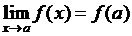 .
.
То есть  непрерывна в точке а, если: 1)
непрерывна в точке а, если: 1)  определена в некоторой
определена в некоторой  ; 2)
; 2)  ; 3)
; 3) 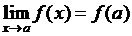 .
.
На языке  это определение можно записать в виде:
это определение можно записать в виде:
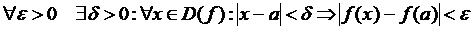 или
или
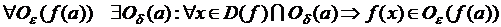 .
.
О. Функция  называется непрерывной слева в точке а, если она определена на
называется непрерывной слева в точке а, если она определена на 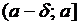 и
и 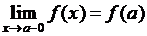 .
.
О. Функция  называется непрерывной справа в точке а, если она определена на
называется непрерывной справа в точке а, если она определена на 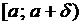 и
и 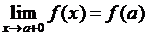 .
.
Точки разрыва
О. Точка а называется точкой разрыва функции  , если в этой точке функция
, если в этой точке функция  не является непрерывной.
не является непрерывной.
Т.е. а − точка разрыва функции  , если выполняется одно из условий: 1)
, если выполняется одно из условий: 1)  не определена в точке а; 2) не существует
не определена в точке а; 2) не существует 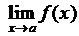 ;
;
3)  .
.
О. Пусть точка а − точка разрыва функции  . Если в этой точке существуют конечные пределы слева и справа, но они не равны, то точка а называется точкой разрыва I рода функции
. Если в этой точке существуют конечные пределы слева и справа, но они не равны, то точка а называется точкой разрыва I рода функции  .
.
О. Если  , то точка а называется устранимой точкой разрыва функции
, то точка а называется устранимой точкой разрыва функции  .
.
О. Если в точке а хотя бы один из односторонних пределов не существует или бесконечен, то точка а – точка разрыва II рода функции  .
.
Примеры 1)  точка разрыва I рода;
точка разрыва I рода;
2)  –устранимая точка разрыва, т.к.
–устранимая точка разрыва, т.к. 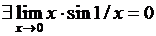 , по теореме о произведении б.м. функции на ограниченную;
, по теореме о произведении б.м. функции на ограниченную;
3) 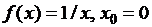 – точка разрыва II рода, т.к.
– точка разрыва II рода, т.к. 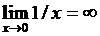 ;
;
4)  – точка разрыва II рода, т.к.
– точка разрыва II рода, т.к. 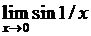 не существует.
не существует.
Производная функции в точке
 5.1 Определение. Физический и геометрический смысл производной
5.1 Определение. Физический и геометрический смысл производной
Пусть  – путь, пройденный материальной точкой за время t. Тогда средняя скорость материальной точки за промежуток
– путь, пройденный материальной точкой за время t. Тогда средняя скорость материальной точки за промежуток  есть величина, равная
есть величина, равная  .
.
Тогда  мгновенная скорость движения материальной точки в момент времени
мгновенная скорость движения материальной точки в момент времени  .
.
Обозначим 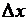 – приращение аргумента х,
– приращение аргумента х,
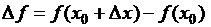 – приращение функции
– приращение функции  , соответ-ствующее приращению
, соответ-ствующее приращению 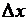 .
.
О. Производной функции в точке  называется число (если оно существует), равное пределу отношения приращения функции в точке
называется число (если оно существует), равное пределу отношения приращения функции в точке  к приращению аргумента при условии, что
к приращению аргумента при условии, что  и обозначается
и обозначается 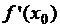 , т. е.
, т. е.  .
.
Механический смысл производной. Если х – время,  – путь, пройденный материальной точкой за время х, то
– путь, пройденный материальной точкой за время х, то 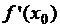 – это скорость движения в момент времени
– это скорость движения в момент времени  или
или 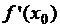 –мгновенная скорость изменения функции
–мгновенная скорость изменения функции  в момент времени
в момент времени  .
.
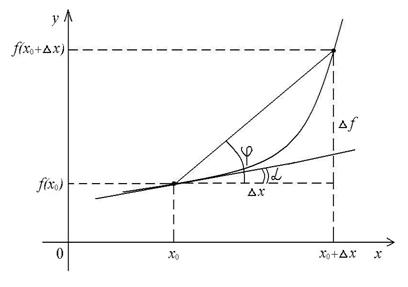
Геометрический смысл производной. 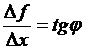 – это тангенс угла наклона секущей, проходящей через точки с координатами
– это тангенс угла наклона секущей, проходящей через точки с координатами  и
и  .
.
При 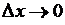
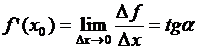 – тангенс угла наклона касательной, проведенной к графику функции
– тангенс угла наклона касательной, проведенной к графику функции  в точке
в точке  .
.
Если  уравнение касательной, то
уравнение касательной, то  .
.
Уравнение касательной: 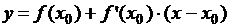 .
.
Примеры 1)  .
.
 , т. е. производная постоянной функции равна 0.
, т. е. производная постоянной функции равна 0.
2) 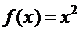 . Покажем, что
. Покажем, что 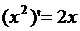 . Действительно,
. Действительно, 
 .
.
3)  .
.

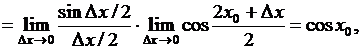 т. е.
т. е.  .
.
Теорема Если  имеет производную в точке
имеет производную в точке  , то
, то  непрерывна в точке
непрерывна в точке  .
.
Замечание. Если  разрывна в точке
разрывна в точке  , то она не имеет производной в точке
, то она не имеет производной в точке  .
.
По аналогии с односторонними пределами вводятся понятия односторонних производных:
 ,
,  – правосторонняя и левосторонняя производные функции
– правосторонняя и левосторонняя производные функции  в точке
в точке  .
.
Пример  . Найти односторонние производные.
. Найти односторонние производные.
Решение. 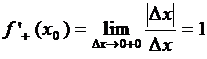 ,
,
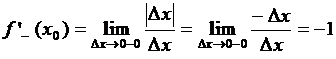 .
.
Так как односторонние производные не равны, то  не имеет производной в точке
не имеет производной в точке  .
.
Дифференциал функции
Пусть функции  определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.
О. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если её приращение в точке
, если её приращение в точке  представимо в виде:
представимо в виде:
 ,
,
где А – постоянная, не зависящая от 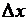 (но зависящая от
(но зависящая от  ), а функция
), а функция 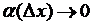 при
при 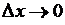 .
.
Слагаемое 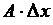 называется дифференциалом функции
называется дифференциалом функции  в точке
в точке  и обозначается
и обозначается  или
или 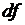 . Дифференциал – это главное линейная часть приращения функции. Тогда
. Дифференциал – это главное линейная часть приращения функции. Тогда  ,
, 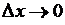 .
.
Теорема Функция  дифференцируема в точке
дифференцируема в точке  тогда, и только тогда, когда она имеет производную в точке
тогда, и только тогда, когда она имеет производную в точке  . При этом
. При этом
 .
.
Обычно 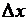 обозначают
обозначают  и пишут
и пишут  .
.
Правила дифференцирования
Теорема 1 Если функции  и
и 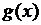 дифференцируемы в точке
дифференцируемы в точке  , то в этой точке дифференцируемы функции
, то в этой точке дифференцируемы функции

 (если
(если 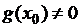 ),
),
причем 1)  ,
,
2)  ,
,
3)  ,
,  .
.
Следствие  , где
, где  .
.
Теорема 3 (дифференцирование сложной функции) Если 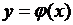 дифференцируема в точке
дифференцируема в точке  ,
,  дифференцируема в точке
дифференцируема в точке  , то сложная функция
, то сложная функция  дифференцируема в точке
дифференцируема в точке 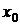 , причем
, причем 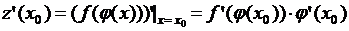 .
.
Таблица производных от основных элементарных функций
1) 
2) 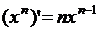 ,
, 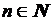 ,
,  ,
, 
3) 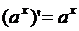 ,
, 
4)  ,
, 
5)  , 6)
, 6) 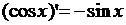
7)  , 8)
, 8) 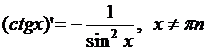

9)  , 10)
, 10) 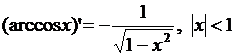
11)  , 12)
, 12) 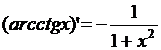
13)  , 14)
, 14) 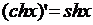
15)  , 16)
, 16) 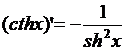
Точки локального экстремума
О. Функция  имеет в точке
имеет в точке  локальный максимум, если существует такая окрестность
локальный максимум, если существует такая окрестность 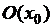 точки
точки  , что
, что
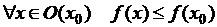 .
.
О.  – точка строгого локального максимума, если
– точка строгого локального максимума, если
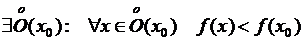 .
.
О. Функция  имеет в точке
имеет в точке  локальный минимум, если существует такая окрестность
локальный минимум, если существует такая окрестность 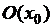 точки
точки  , что
, что
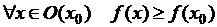 .
.
О.  – точка строгого локального максимума, если
– точка строгого локального максимума, если
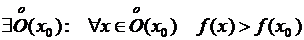 .
.
Локальный максимум и локальный минимум объединяются названием локальный экстремум.
Теорема Ферма
Теорема Ферма Если  имеет в точке
имеет в точке  локальный экстремум и дифференцируема в этой точке, то
локальный экстремум и дифференцируема в этой точке, то  .
.
Геометрический смысл теоремы Ферма: касательная к графику функции  в точке локального экстремума параллельна оси Ох.
в точке локального экстремума параллельна оси Ох.
Теорема Ролля
Теорема Ролля (о нулях производной) Если  непрерывна на отрезке
непрерывна на отрезке  , принимает в концах этого отрезка равные значения
, принимает в концах этого отрезка равные значения  и дифференцируема на интервале
и дифференцируема на интервале  , то существует точка
, то существует точка 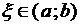 , в которой
, в которой  .
.
Геометрический смысл теоремы Ролля: при условиях теоремы Ролля существует точка 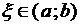 , в которой касательная к графику функции
, в которой касательная к графику функции  параллельна оси Ох.
параллельна оси Ох.
6.4 Формула Лагранжа конечных приращений.
Теорема Лагранжа Если  непрерывна на отрезке
непрерывна на отрезке  и дифференцируема на интервале
и дифференцируема на интервале  , то существует такая точка
, то существует такая точка 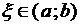 , что
, что  .
.
Геометрический смысл теоремы Лагранжа:  , в которой касательная к графику функции
, в которой касательная к графику функции  параллельна секущей, соединяющей точки
параллельна секущей, соединяющей точки  и
и  .
.
Следствия 1)Если функция  дифференцируема на интервале
дифференцируема на интервале  и
и 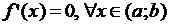 , то
, то 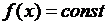 на
на 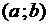 .
.
2) Если  на
на  , то
, то  не убывает на
не убывает на  .
.
Если 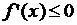 на
на  , то
, то  не возрастает на
не возрастает на  .
.
3) Если две непрерывные функции имеют одинаковые производные, то они отличаются на  , т.е.
, т.е. 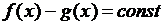 .
.
Правило Лопиталя
Теорема 1 Пусть  и
и 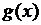 дифференцируемы на интервале
дифференцируемы на интервале  ,
, 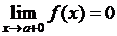 ,
,  ,
, 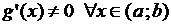 и существует конечный или бесконечный
и существует конечный или бесконечный  . Тогда
. Тогда  тоже существует и равен А, т.е.
тоже существует и равен А, т.е. 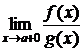
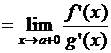 .
.
Замечание. Утверждение теоремы справедливо и при  , и при
, и при 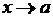 , и при
, и при 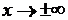 .
.
Теорема 2 Пусть 1)  и
и 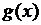 дифференцируемы при
дифференцируемы при  , причем
, причем 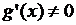 при
при  ;
;
2)  ,
, 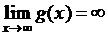 ;
;
3) существует конечный  .
.
Тогда существует 
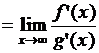 .
.
Замечание. Правило Лопиталя служит для раскрытия неопреде-ленностей вида  и
и  . Иногда к этим неопределенностям удается свести неопределенности
. Иногда к этим неопределенностям удается свести неопределенности 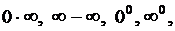
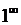 .
.
Экстремумы функции
О. Точки, в которых  , называются стационарными.
, называются стационарными.
О. Точки, в которых  непрерывна, а
непрерывна, а  или не существует, называются критическими
или не существует, называются критическими
Из теоремы Ферма следует, что если 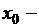 точка экстремума, то
точка экстремума, то 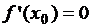 . Поэтому точки экстремума следует искать среди критических точек.
. Поэтому точки экстремума следует искать среди критических точек.
Однако не всякая критическая точка является точкой экстремума. Например, для  , но
, но  не является точкой экстремума.
не является точкой экстремума.
Теорема (I достаточное условие строгого экстремума) Пусть  дифференцируема в некоторой
дифференцируема в некоторой  и непрерывна в точке
и непрерывна в точке  . Тогда 1) если
. Тогда 1) если 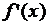 меняет знак с минуса на плюс при переходе через точку
меняет знак с минуса на плюс при переходе через точку  , т.е.
, т.е. 

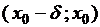
 , а
, а 
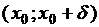
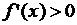 , то
, то  – точка строгого локального минимума функции
– точка строгого локального минимума функции  ;
;
2) если 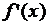 меняет знак с плюса на минус при переходе через точку
меняет знак с плюса на минус при переходе через точку  , то
, то  – точка строгого локального максимума функции
– точка строгого локального максимума функции  .
.
Выпуклость функции
О. Функция  называется выпуклой вверх на отрезке
называется выпуклой вверх на отрезке  , если
, если 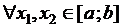 выполняется неравенство:
выполняется неравенство:  .
.
То есть для любых двух точек 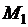 и
и 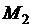



 – принадлежит,
– принадлежит, – содержится,
– содержится, – любой, для любого, каждый, для всех и т. п.,
– любой, для любого, каждый, для всех и т. п., – существует, найдется,
– существует, найдется, – знак следования (в записи
– знак следования (в записи  условие А называется достаточным для В, условие В называется необходимым для А),
условие А называется достаточным для В, условие В называется необходимым для А),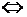 – знак равносильности (означает, что
– знак равносильности (означает, что  ),
), .
. :
: 
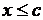 .
. :
:  .
. называется нижней гранью множества Х.
называется нижней гранью множества Х. :
:  .
.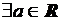 :
:  .
.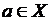 :
: 
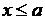 .
.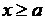 .
.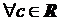 :
:  :
: 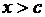 .
. :
: 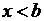 .
. (супремум), если
(супремум), если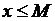 ; 2)
; 2)  .
. .
. (инфинум), если
(инфинум), если ; 2)
; 2) 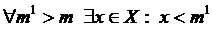 .
. .
.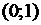 .
.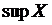 .
. , если Х не ограничено снизу, то
, если Х не ограничено снизу, то 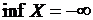 .
. .
. .
. N
N  .
. целое,
целое,  натуральное
натуральное  .
. . Иррациональное число – это всегда бесконечная непериодическая десятичная дробь.
. Иррациональное число – это всегда бесконечная непериодическая десятичная дробь. 2 Числовые последовательности
2 Числовые последовательности или
или  . Множество Х при этом называется областью определения, а множество Y – областью значений.
. Множество Х при этом называется областью определения, а множество Y – областью значений.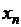 – n -ый член последовательности,
– n -ый член последовательности,  .
. :
: 
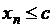 .
. :
: 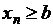 .
. .
.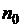 , если
, если 
 .
. .
. .
.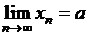 .
. окрестностью
окрестностью  точки а называется симметричный интервал
точки а называется симметричный интервал  . Следующие записи равносильны:
. Следующие записи равносильны: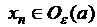
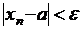
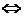
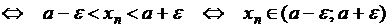 .
.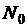 , что все члены последовательности с номерами, большими, чем этот, принадлежат этой окрестности, т.е.
, что все члены последовательности с номерами, большими, чем этот, принадлежат этой окрестности, т.е.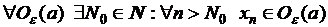 .
.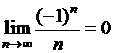 , так как
, так как
 , то говорят, что последовательность
, то говорят, что последовательность 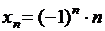 не имеет предела, так как нет такого числа, в окрестности которого находились бы все члены этой последовательности, начиная с некоторого номера.
не имеет предела, так как нет такого числа, в окрестности которого находились бы все члены этой последовательности, начиная с некоторого номера.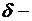 окрестностью точки a называется множество
окрестностью точки a называется множество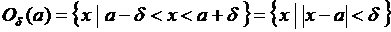 .
.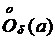 .
. в точке a, если
в точке a, если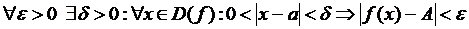 ,
,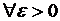 найдется такое
найдется такое 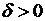 , что для
, что для 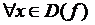 , отличающегося от a меньше, чем на
, отличающегося от a меньше, чем на 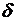 , и не равного a, выполняется неравенство
, и не равного a, выполняется неравенство 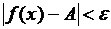 .
.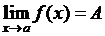 .
.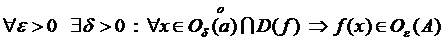 .
.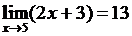
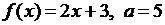 . Нужно доказать, что
. Нужно доказать, что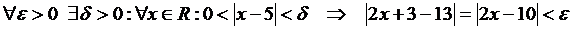 .
.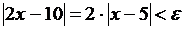 , если
, если 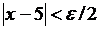 . Т. о.,
. Т. о.,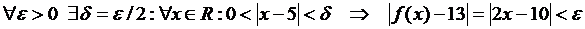 .
.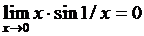
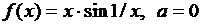 ,
, 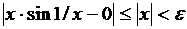 , если взять
, если взять 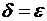 .
.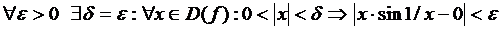 .
.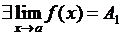 и
и 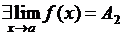 , причем для определенности будем считать, что
, причем для определенности будем считать, что 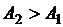 .
.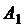 и
и 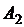 . Так как
. Так как 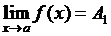 , то для
, то для 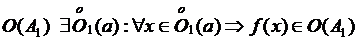 . Т. к.
. Т. к.  , то для
, то для 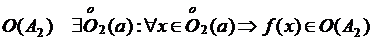 .
.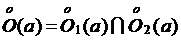 . Тогда
. Тогда 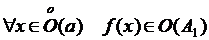 и
и 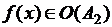 . Противоречие. ■
. Противоречие. ■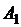 называется пределом слева функции
называется пределом слева функции 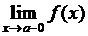 , если
, если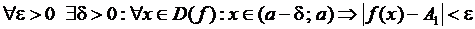 .
.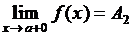 означает, что
означает, что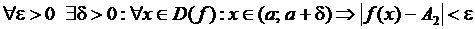 .
.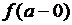 и
и 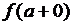 .
.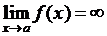 , если
, если 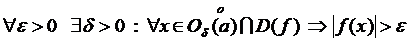 .
.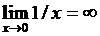 .
.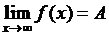 , если
, если 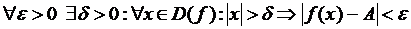 .
.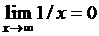 .
.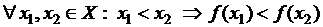 .
. .
.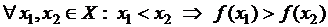 .
. .
.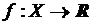 имела предел при
имела предел при  или
или  , необходимо и достаточно, чтобы функция
, необходимо и достаточно, чтобы функция 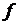 была ограничена на Х сверху.
была ограничена на Х сверху.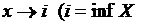 или
или  , необходимо и достаточно, чтобы функция
, необходимо и достаточно, чтобы функция  , то функцию
, то функцию 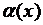 называют бесконечно малой при
называют бесконечно малой при 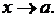
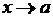 есть б.м. функция при
есть б.м. функция при 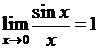 .
.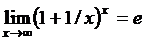
 , получим
, получим .
.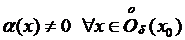 и
и 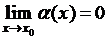 , то
, то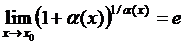 .
. .
.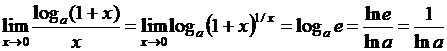 .
. получим
получим 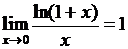 .
.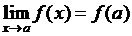 .
. ; 2)
; 2)  ; 3)
; 3)  это определение можно записать в виде:
это определение можно записать в виде: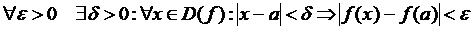 или
или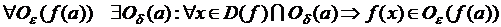 .
.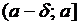 и
и 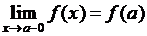 .
.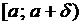 и
и 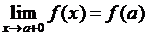 .
.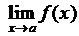 ;
; .
. , то точка а называется устранимой точкой разрыва функции
, то точка а называется устранимой точкой разрыва функции  точка разрыва I рода;
точка разрыва I рода; –устранимая точка разрыва, т.к.
–устранимая точка разрыва, т.к. 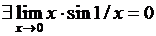 , по теореме о произведении б.м. функции на ограниченную;
, по теореме о произведении б.м. функции на ограниченную;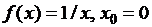 – точка разрыва II рода, т.к.
– точка разрыва II рода, т.к.  – точка разрыва II рода, т.к.
– точка разрыва II рода, т.к. 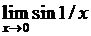 не существует.
не существует. – путь, пройденный материальной точкой за время t. Тогда средняя скорость материальной точки за промежуток
– путь, пройденный материальной точкой за время t. Тогда средняя скорость материальной точки за промежуток  есть величина, равная
есть величина, равная  .
. мгновенная скорость движения материальной точки в момент времени
мгновенная скорость движения материальной точки в момент времени  .
.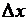 – приращение аргумента х,
– приращение аргумента х,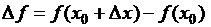 – приращение функции
– приращение функции  называется число (если оно существует), равное пределу отношения приращения функции в точке
называется число (если оно существует), равное пределу отношения приращения функции в точке  и обозначается
и обозначается 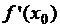 , т. е.
, т. е.  .
. – путь, пройденный материальной точкой за время х, то
– путь, пройденный материальной точкой за время х, то 
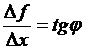 – это тангенс угла наклона секущей, проходящей через точки с координатами
– это тангенс угла наклона секущей, проходящей через точки с координатами  и
и  .
.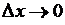
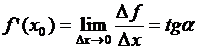 – тангенс угла наклона касательной, проведенной к графику функции
– тангенс угла наклона касательной, проведенной к графику функции  уравнение касательной, то
уравнение касательной, то  .
.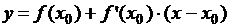 .
. .
. , т. е. производная постоянной функции равна 0.
, т. е. производная постоянной функции равна 0.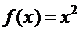 . Покажем, что
. Покажем, что 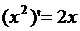 . Действительно,
. Действительно, 
 .
. .
.
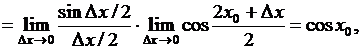 т. е.
т. е.  .
. ,
,  – правосторонняя и левосторонняя производные функции
– правосторонняя и левосторонняя производные функции  . Найти односторонние производные.
. Найти односторонние производные.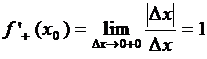 ,
,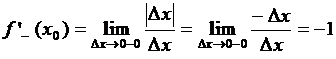 .
. не имеет производной в точке
не имеет производной в точке  .
. ,
,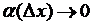 при
при 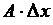 называется дифференциалом функции
называется дифференциалом функции  или
или 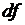 . Дифференциал – это главное линейная часть приращения функции. Тогда
. Дифференциал – это главное линейная часть приращения функции. Тогда  ,
,  .
. и пишут
и пишут  .
.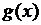 дифференцируемы в точке
дифференцируемы в точке 
 (если
(если 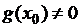 ),
), ,
, ,
, ,
,  .
. , где
, где  .
.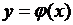 дифференцируема в точке
дифференцируема в точке  дифференцируема в точке
дифференцируема в точке  , то сложная функция
, то сложная функция  дифференцируема в точке
дифференцируема в точке 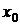 , причем
, причем 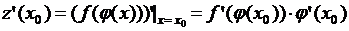 .
.
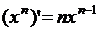 ,
, 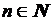 ,
,  ,
, 
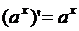 ,
, 
 ,
, 
 , 6)
, 6) 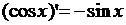
 , 8)
, 8) 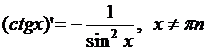

 , 10)
, 10) 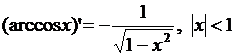
 , 12)
, 12) 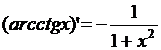
 , 14)
, 14) 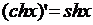
 , 16)
, 16) 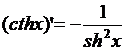
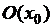 точки
точки 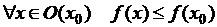 .
.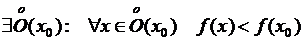 .
.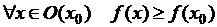 .
.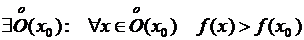 .
. .
. , принимает в концах этого отрезка равные значения
, принимает в концах этого отрезка равные значения  и дифференцируема на интервале
и дифференцируема на интервале  , то существует точка
, то существует точка 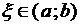 , в которой
, в которой  .
. .
. , в которой касательная к графику функции
, в которой касательная к графику функции  и
и  .
.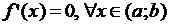 , то
, то 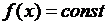 на
на 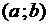 .
. на
на 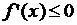 на
на  , т.е.
, т.е. 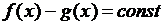 .
.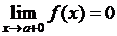 ,
,  ,
, 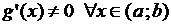 и существует конечный или бесконечный
и существует конечный или бесконечный  . Тогда
. Тогда  тоже существует и равен А, т.е.
тоже существует и равен А, т.е. 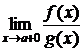
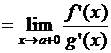 .
. , и при
, и при 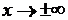 .
. , причем
, причем 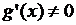 при
при  ,
, 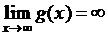 ;
; .
.
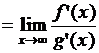 .
. и
и  . Иногда к этим неопределенностям удается свести неопределенности
. Иногда к этим неопределенностям удается свести неопределенности 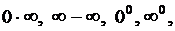
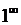 .
. , называются стационарными.
, называются стационарными.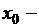 точка экстремума, то
точка экстремума, то 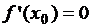 . Поэтому точки экстремума следует искать среди критических точек.
. Поэтому точки экстремума следует искать среди критических точек. , но
, но  и непрерывна в точке
и непрерывна в точке 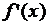 меняет знак с минуса на плюс при переходе через точку
меняет знак с минуса на плюс при переходе через точку 

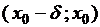
 , а
, а 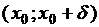
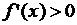 , то
, то 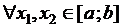 выполняется неравенство:
выполняется неравенство:  .
.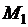 и
и