Если 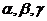 - углы, образованные соответственно с положительными направлениями осей
- углы, образованные соответственно с положительными направлениями осей 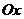 ,
, 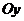 и
и 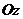 , единичной нормалью n к выбранной стороне
, единичной нормалью n к выбранной стороне 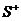 поверхности S, тогда связь поверхностных интегралов первого и второго рода выражается следующим равенством
поверхности S, тогда связь поверхностных интегралов первого и второго рода выражается следующим равенством
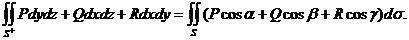
Поскольку n 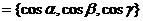 , то поверхностный интеграл первого рода в правой части этого равенства можно записать компактно в векторной форме
, то поверхностный интеграл первого рода в правой части этого равенства можно записать компактно в векторной форме
 F · n
F · n 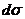 ,
,
где F 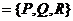 - векторное поле, определенное на S.
- векторное поле, определенное на S.
Векторное поле F можно ассоциировать с полем скоростей жидкости, протекающей через поверхность S. Тогда интеграл
 F · n
F · n 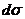
можно истолковывать механически как общее количество жидкости, протекающее в единицу времени через поверхность 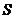 в положительном направлении, т. е. вдоль n. Поэтому этот интеграл называется потоком векторного поля F через поверхность
в положительном направлении, т. е. вдоль n. Поэтому этот интеграл называется потоком векторного поля F через поверхность 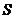 .
.
Пример 1. Вычислить поверхностный интеграл первого рода
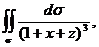
где у – часть плоскости 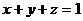 , заключенная в первом октанте.
, заключенная в первом октанте.
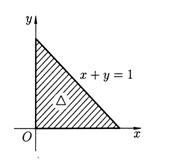
Рис. 36.
Поверхность у можно выразить явно: 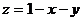 ,
,  , где область
, где область 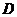 - треугольник, ограниченный прямыми
- треугольник, ограниченный прямыми 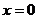 ,
, 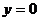 и
и 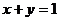 (рис. 36). При этом
(рис. 36). При этом 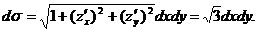 Данный интеграл сводится к двойному (при этом знаменатель подынтегральной функции равен
Данный интеграл сводится к двойному (при этом знаменатель подынтегральной функции равен 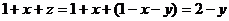 ):
):
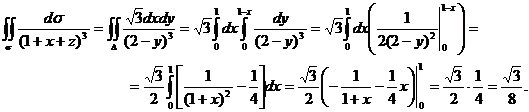
Пример 2. Вычислить поверхностный интеграл первого рода
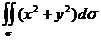 ,
,
где у – сфера  .
.
В силу симметрии относительно координатных плоскостей поверхности у и подынтегральной функции ограничимся вычислением интеграла при условии 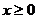 ,
, 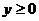 ,
, 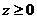 , а результат умножим на 8.
, а результат умножим на 8.
Используя сферические координаты, запишем параметрические уравнения сферы 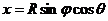 ,
, 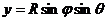 ,
, 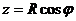 , учитывая, что
, учитывая, что 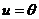 ,
, 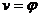 . Тогда
. Тогда
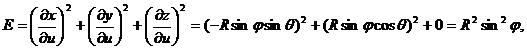
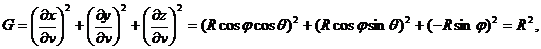
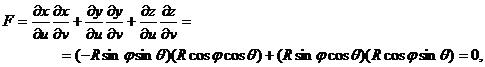
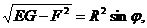
а область интегрирования – четверть круга 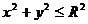 в параметрической форме имеет вид
в параметрической форме имеет вид
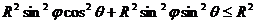 ,
, 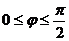 ,
, 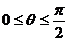 .
.
Остается выразить через параметры подынтегральную функцию 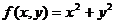 . На сфере
. На сфере  имеем
имеем 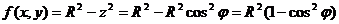 . Таким образом данный интеграл равен
. Таким образом данный интеграл равен
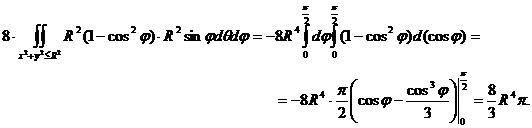
Пример 3. Вычислить поверхностный интеграл второго рода
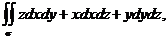
где у – внешняя поверхность плоскости 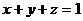 , ограниченной координатными плоскостями.
, ограниченной координатными плоскостями.
Интеграл будем вычислять покомпонентно, проектируя у на разные координатные плоскости (рис. 37).
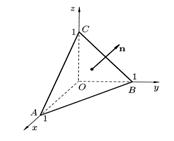
Рис. 37.
Вычислим
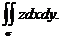
Выражая явно 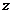 через
через 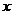 и
и 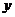 , сведем этот интеграл к двойному интегралу по
, сведем этот интеграл к двойному интегралу по 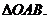 Подставляя
Подставляя 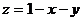 в подынтегральную функцию и учитывая, что:
в подынтегральную функцию и учитывая, что: 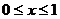 ,
, 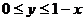 , получаем
, получаем
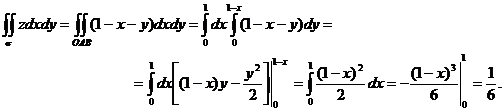
Остальные интегралы
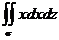 и
и 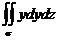
приводят к такому же результату. Поэтому искомый интеграл равен 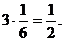
Пример 4. Найти поток векторного поля F (x, y, z) 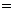 x i + y j + z k через часть поверхности эллипсоида
x i + y j + z k через часть поверхности эллипсоида

лежащую в первом октанте в направлении внешней нормали.
Искомый поток равен
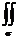 F · n
F · n 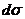 =
= 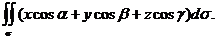
Последний интеграл сводится к поверхностным интегралам второго рода
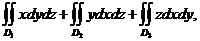
где 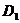 ,
, 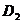 ,
, 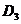 - проекции эллипсоида на соответствующие координатные плоскости.
- проекции эллипсоида на соответствующие координатные плоскости.
Рассмотрим, например,
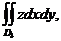
где 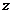 можно выразить через
можно выразить через 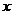 и
и 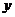 из уравнения эллипсоида,
из уравнения эллипсоида, 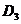 - внутренность четверти эллипса
- внутренность четверти эллипса
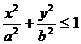 ,
, 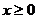 ,
, 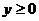 .
.
Очевидно, что
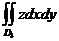
равен объему восьмой части эллипсоида, которая, как известно, равна 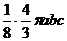 . Аналогично находим и другие интегралы, отсюда получаем, что исходный интеграл первого рода, т. е. поток векторного поля, равен
. Аналогично находим и другие интегралы, отсюда получаем, что исходный интеграл первого рода, т. е. поток векторного поля, равен 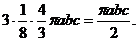
Пример 5. Найти поток вектора F 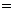
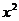 i
i 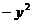 j
j 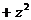 k через поверхность тела, ограниченного сферой
k через поверхность тела, ограниченного сферой 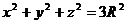 , плоскостью
, плоскостью 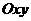 и однополостным гиперболоидом
и однополостным гиперболоидом 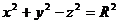 .
.
Имеем
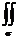 F · n
F · n 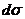
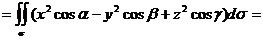
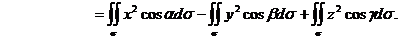
На плоскости 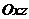 и
и 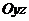 поверхность у проектируется дважды, с обеих сторон, к тому же поверхность у симметрична относительно этих плоскостей. Поэтому соответствующие интегралы получаются нулевыми:
поверхность у проектируется дважды, с обеих сторон, к тому же поверхность у симметрична относительно этих плоскостей. Поэтому соответствующие интегралы получаются нулевыми:
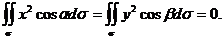
А теперь вычислим
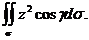
Поверхность у состоит из трех частей (рис. 38):
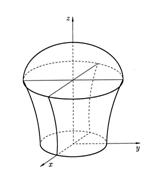
Рис. 38.
а) сегмент сферы 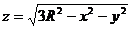 , для которого
, для которого 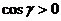 (внешняя нормаль образует с
(внешняя нормаль образует с 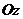 острый угол); проекция этого сегмента на
острый угол); проекция этого сегмента на 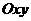 есть круг
есть круг 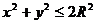 (сегмент сферы
(сегмент сферы 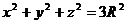 пересекается с гиперболоидом
пересекается с гиперболоидом 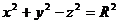 по линии
по линии
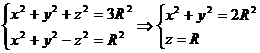 —
—
окружность радиуса 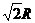 );
);
б) сегмент параболоида проектируется на 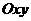 в кольцо
в кольцо 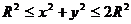 ,
, 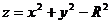 (из уравнения гиперболоида);
(из уравнения гиперболоида);
в) третья часть – это круг 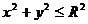 , на котором
, на котором 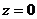 .
.
Поэтому 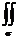 F · n
F · n 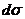
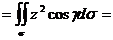
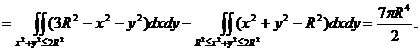
Пример 6. Найти массу полусферы  ,
, 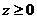 радиуса
радиуса 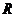 с поверхностной плотностью, равной
с поверхностной плотностью, равной 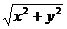 .
.
Имеем
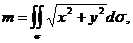
где
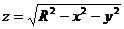 ,
, 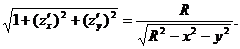
Следовательно,

Переходя к полярным координатам в двойном интеграле, получаем
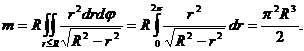
Контрольные вопросы:
- Дайте определение поверхностного интеграла первого рода.
- Дайте определение поверхностного интеграла второго рода.
- Приведите формулу для вычисления статических моментов поверхности относительно координатных плоскостей.
- Приведите формулу для вычисления моментов инерции относительно координатных осей и начала координат.
- В чем заключается связь поверхностных интегралов первого и второго рода?
Задания для самостоятельного решения:
1. Вычислить следующие криволинейные интегралы первого рода:
а) 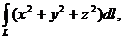
 - дуга цепной линии
- дуга цепной линии 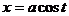 ,
, 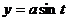 ,
, 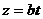 ,
, 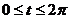 ;
;
б) 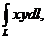
 - четверть эллипса
- четверть эллипса 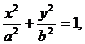
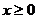 ,
, 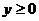 .
.
2. Найти координаты центра тяжести дуги циклоиды 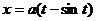 ,
, 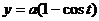 ,
, 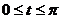 .
.
3. Вычислить массу:
а) четверти эллипса 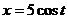 ,
, 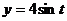 , расположенную в первой четверти, если ее линейная плотность
, расположенную в первой четверти, если ее линейная плотность 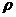 равна у.
равна у.
б) контура прямоугольника со сторонами, лежащими на прямых 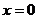 ,
, 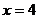 ,
, 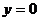 ,
, 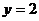 , если
, если 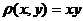 ;
;
в) дуги параболы 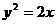 , заключенной между точками О (0,0) и
, заключенной между точками О (0,0) и 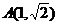 , если
, если 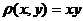 .
.
4. Вычислить площади цилиндрических поверхностей, ограниченных снизу плоскостью 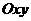 , а сверху поверхностью
, а сверху поверхностью 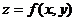 , при условии, что известна направляющая
, при условии, что известна направляющая  этой цилиндрической поверхности:
этой цилиндрической поверхности:
а) 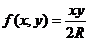 ,
, 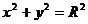 ;
;
б) 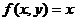 ,
, 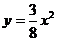 (
(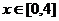 ).
).
5. С помощью криволинейного интеграла первого рода найти координаты центра тяжести кривых:
а) 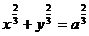 ,
, 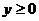 ;
;
б) 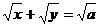 (
(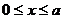 ).
).
6. Вычислить криволинейный интеграл:
а) 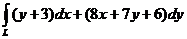 ,
,
по разным путям, соединяющим точки 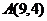 ,
, 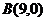 ,
, 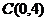 :
:
1)  - отрезок ОА;
- отрезок ОА;
2)  - ломаная ОВА;
- ломаная ОВА;
3)  - ломаная ОСА;
- ломаная ОСА;
4)  - парабола, соединяющая точки
- парабола, соединяющая точки 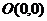 и
и 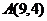 и симметричная относительно оси
и симметричная относительно оси 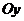 .
.
5) проверить выполнение условия Грина.
б) 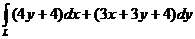
по разным путям, соединяющим точки 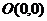 ,
, 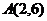 ,
,  ,
, 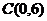 :
:
1) 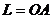 ;
;
2) 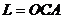 ;
;
3) 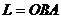 ;
;
4)  - дуга
- дуга 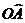 параболы
параболы 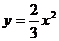 .
.
в) 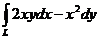 ,
,
взятый вдоль различных путей, соединяющих точки 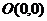 ,
,  ,
,  ,
,  :
:
1)  - отрезок ОА;
- отрезок ОА;
2)  - парабола с осью симметрии
- парабола с осью симметрии 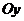 , проходящая через точки О и А;
, проходящая через точки О и А;
3)  - парабола, проходящая через точки О и А с осью симметрии
- парабола, проходящая через точки О и А с осью симметрии 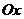 ;
;
4)  - ломаная ОВА;
- ломаная ОВА;
5)  - ломаная ОСА.
- ломаная ОСА.
7. Вычислить:
а) 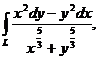 где
где  - дуга кривой
- дуга кривой 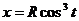 ,
, 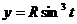 , пробегая от точки
, пробегая от точки 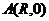 к
к 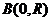 .
.
б) 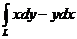 , где линия L – задана уравнениями
, где линия L – задана уравнениями 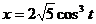 ,
, 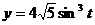 ,
, 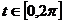 .
.
в) 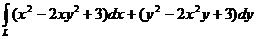 , где L – дуга параболы
, где L – дуга параболы 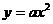 , соединяющей точки
, соединяющей точки 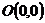 и
и  .
.
8. Вычислить криволинейные интегралы:
а) 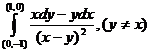 .
.
б) 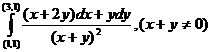 .
.
9. Применяя формулу Грина, вычислить криволинейные интегралы:
а) 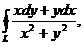 где
где  - окружность
- окружность 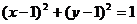 , пробегаемая против часовой стрелки.
, пробегаемая против часовой стрелки.
б) 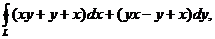
 - эллипс
- эллипс 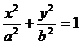 .
.
10. Найти работу силы:
а) F = 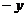 i +
i + 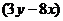 j при перемещении материальной точки вдоль контура прямоугольника с вершинами
j при перемещении материальной точки вдоль контура прямоугольника с вершинами 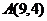 ,
,  ,
, 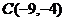 ,
, 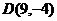 .
.
б) F = 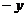 i +
i + 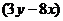 j при перемещении материальной точки вдоль эллипса
j при перемещении материальной точки вдоль эллипса
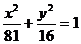 .
.
11. Вычислить поверхностные интегралы первого рода:
а) 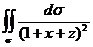 , где часть плоскости
, где часть плоскости 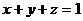 при условии
при условии 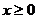 ,
, 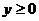 ,
, 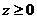 .
.
б) 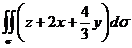 , часть плоскости
, часть плоскости 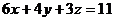 , лежащая в первом октанте.
, лежащая в первом октанте.
в) 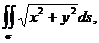 где
где 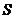 - боковая поверхность конуса
- боковая поверхность конуса 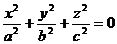 (
(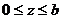 ).
).
12. Вычислить следующие интегралы второго рода:
а) 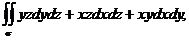 где у – внешняя сторона тетраэдра, ограниченного плоскостями
где у – внешняя сторона тетраэдра, ограниченного плоскостями 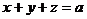 ,
, 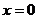 ,
, 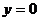 ,
, 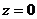 .
.
б) 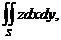 где
где 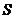 - внешняя сторона эллипсоида
- внешняя сторона эллипсоида

в) 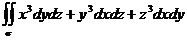 , где у – внешняя сторона сферы
, где у – внешняя сторона сферы 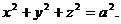
13. Найти поток вектора:
а) F 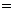
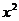 i
i 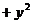 j
j 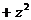 k через поверхность тела
k через поверхность тела 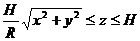 в направлении внешней нормали.
в направлении внешней нормали.
б) F 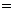 2 x i - y j через часть поверхности цилиндра
2 x i - y j через часть поверхности цилиндра 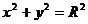 ,
, 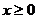 ,
, 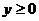 ,
, 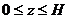 в направлении внешней нормали.
в направлении внешней нормали.
14. Найти массу поверхности:
а) куба 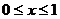 ,
, 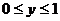 ,
, 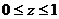 , если поверхностная плотность в каждой точке
, если поверхностная плотность в каждой точке 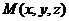 равна
равна 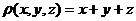 .
.
б) куба 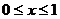 ,
, 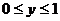 ,
, 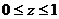 , если поверхностная плотность в каждой точке
, если поверхностная плотность в каждой точке 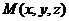 равна
равна 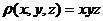 .
.



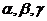 - углы, образованные соответственно с положительными направлениями осей
- углы, образованные соответственно с положительными направлениями осей 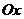 ,
, 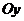 и
и 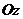 , единичной нормалью n к выбранной стороне
, единичной нормалью n к выбранной стороне 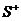 поверхности S, тогда связь поверхностных интегралов первого и второго рода выражается следующим равенством
поверхности S, тогда связь поверхностных интегралов первого и второго рода выражается следующим равенством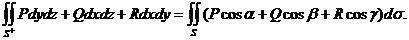
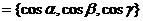 , то поверхностный интеграл первого рода в правой части этого равенства можно записать компактно в векторной форме
, то поверхностный интеграл первого рода в правой части этого равенства можно записать компактно в векторной форме F · n
F · n 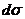 ,
,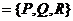 - векторное поле, определенное на S.
- векторное поле, определенное на S.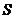 в положительном направлении, т. е. вдоль n. Поэтому этот интеграл называется потоком векторного поля F через поверхность
в положительном направлении, т. е. вдоль n. Поэтому этот интеграл называется потоком векторного поля F через поверхность 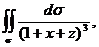
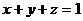 , заключенная в первом октанте.
, заключенная в первом октанте.
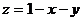 ,
,  , где область
, где область 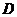 - треугольник, ограниченный прямыми
- треугольник, ограниченный прямыми 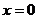 ,
, 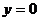 и
и 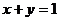 (рис. 36). При этом
(рис. 36). При этом 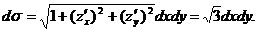 Данный интеграл сводится к двойному (при этом знаменатель подынтегральной функции равен
Данный интеграл сводится к двойному (при этом знаменатель подынтегральной функции равен 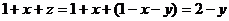 ):
):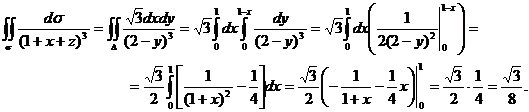
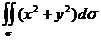 ,
, .
.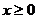 ,
, 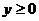 ,
, 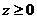 , а результат умножим на 8.
, а результат умножим на 8.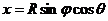 ,
, 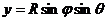 ,
, 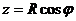 , учитывая, что
, учитывая, что 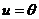 ,
, 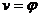 . Тогда
. Тогда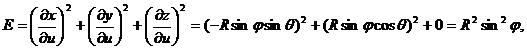
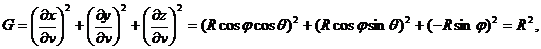
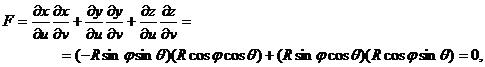
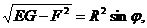
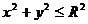 в параметрической форме имеет вид
в параметрической форме имеет вид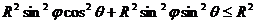 ,
, 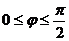 ,
, 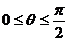 .
.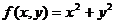 . На сфере
. На сфере 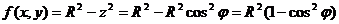 . Таким образом данный интеграл равен
. Таким образом данный интеграл равен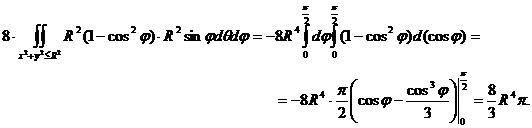
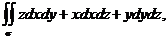

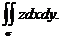
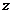 через
через 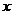 и
и 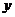 , сведем этот интеграл к двойному интегралу по
, сведем этот интеграл к двойному интегралу по 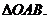 Подставляя
Подставляя 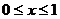 ,
, 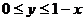 , получаем
, получаем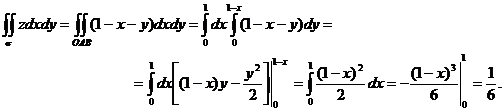
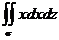 и
и 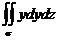
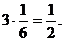
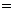 x i + y j + z k через часть поверхности эллипсоида
x i + y j + z k через часть поверхности эллипсоида
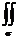 F · n
F · n 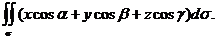
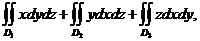
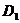 ,
, 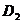 ,
, 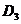 - проекции эллипсоида на соответствующие координатные плоскости.
- проекции эллипсоида на соответствующие координатные плоскости.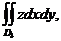
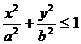 ,
, 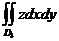
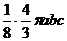 . Аналогично находим и другие интегралы, отсюда получаем, что исходный интеграл первого рода, т. е. поток векторного поля, равен
. Аналогично находим и другие интегралы, отсюда получаем, что исходный интеграл первого рода, т. е. поток векторного поля, равен 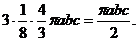
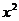 i
i 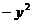 j
j 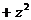 k через поверхность тела, ограниченного сферой
k через поверхность тела, ограниченного сферой 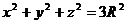 , плоскостью
, плоскостью 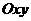 и однополостным гиперболоидом
и однополостным гиперболоидом 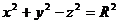 .
.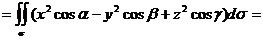
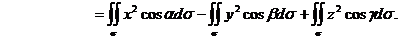
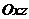 и
и 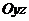 поверхность у проектируется дважды, с обеих сторон, к тому же поверхность у симметрична относительно этих плоскостей. Поэтому соответствующие интегралы получаются нулевыми:
поверхность у проектируется дважды, с обеих сторон, к тому же поверхность у симметрична относительно этих плоскостей. Поэтому соответствующие интегралы получаются нулевыми: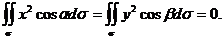
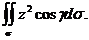

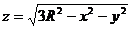 , для которого
, для которого 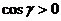 (внешняя нормаль образует с
(внешняя нормаль образует с 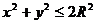 (сегмент сферы
(сегмент сферы 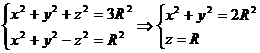 —
—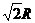 );
);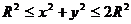 ,
, 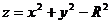 (из уравнения гиперболоида);
(из уравнения гиперболоида);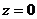 .
.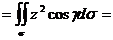
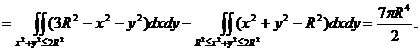
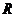 с поверхностной плотностью, равной
с поверхностной плотностью, равной 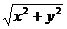 .
.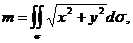
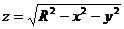 ,
, 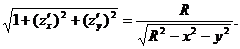

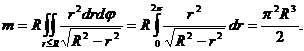
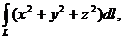
 - дуга цепной линии
- дуга цепной линии 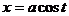 ,
, 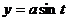 ,
, 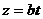 ,
, 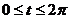 ;
;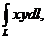
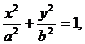
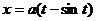 ,
, 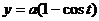 ,
, 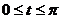 .
.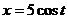 ,
, 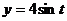 , расположенную в первой четверти, если ее линейная плотность
, расположенную в первой четверти, если ее линейная плотность 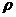 равна у.
равна у.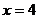 ,
, 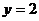 , если
, если 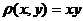 ;
;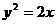 , заключенной между точками О (0,0) и
, заключенной между точками О (0,0) и 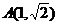 , если
, если 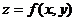 , при условии, что известна направляющая
, при условии, что известна направляющая 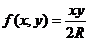 ,
, 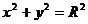 ;
;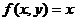 ,
, 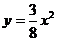 (
(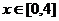 ).
).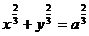 ,
, 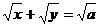 (
(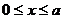 ).
).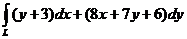 ,
,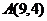 ,
, 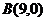 ,
, 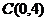 :
: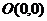 и
и 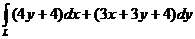
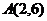 ,
,  ,
, 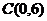 :
: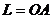 ;
;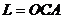 ;
;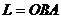 ;
;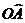 параболы
параболы 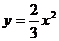 .
.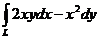 ,
, ,
,  :
: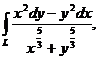 где
где 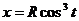 ,
, 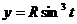 , пробегая от точки
, пробегая от точки 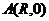 к
к 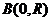 .
.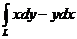 , где линия L – задана уравнениями
, где линия L – задана уравнениями 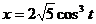 ,
, 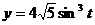 ,
, 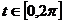 .
.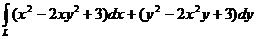 , где L – дуга параболы
, где L – дуга параболы 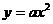 , соединяющей точки
, соединяющей точки 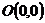 и
и  .
.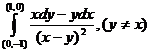 .
.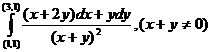 .
.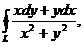 где
где 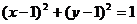 , пробегаемая против часовой стрелки.
, пробегаемая против часовой стрелки.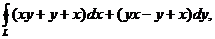
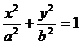 .
.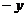 i +
i + 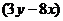 j при перемещении материальной точки вдоль контура прямоугольника с вершинами
j при перемещении материальной точки вдоль контура прямоугольника с вершинами  ,
, 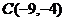 ,
, 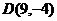 .
.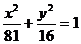 .
.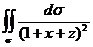 , где часть плоскости
, где часть плоскости 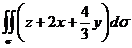 , часть плоскости
, часть плоскости 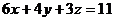 , лежащая в первом октанте.
, лежащая в первом октанте.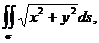 где
где 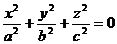 (
(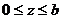 ).
).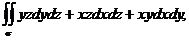 где у – внешняя сторона тетраэдра, ограниченного плоскостями
где у – внешняя сторона тетраэдра, ограниченного плоскостями 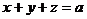 ,
, 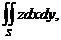 где
где 
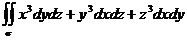 , где у – внешняя сторона сферы
, где у – внешняя сторона сферы 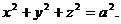
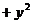 j
j 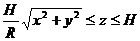 в направлении внешней нормали.
в направлении внешней нормали.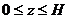 в направлении внешней нормали.
в направлении внешней нормали.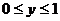 ,
, 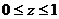 , если поверхностная плотность в каждой точке
, если поверхностная плотность в каждой точке 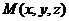 равна
равна 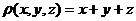 .
.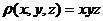 .
.


