

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...
Топ:
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Интересное:
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Интеграл

можно представить в виде скалярного произведения векторов F = P i + Q j и ds = i · dx + j · dy:
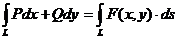 .
.
В таком случае
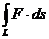
выражает работу переменной силы F = P i + Q j при перемещении материальной точки 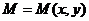 вдоль кривой
вдоль кривой 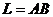 от точки А до точки В.
от точки А до точки В.
При А= В кривая  замкнута, а соответствующий криволинейный интеграл по замкнутой обозначается так:
замкнута, а соответствующий криволинейный интеграл по замкнутой обозначается так:
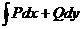 .
.
В этом случае направление обхода контура поясняется стрелкой на кружке, расположенном на знаке интеграла.
Предположим, что в плоскости 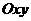 имеется односвязная область
имеется односвязная область 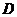 , ограниченная кривой
, ограниченная кривой 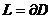 (
( -обозначение границы области
-обозначение границы области 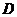 ), а в области
), а в области 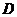 и на границе
и на границе  функции
функции 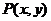 и
и  непрерывны вместе со своими частными производными.
непрерывны вместе со своими частными производными.
Теорема. Пусть А и В – произвольные точки области 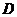 ,
,  и
и 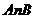 - два произвольных пути (гладкие кривые), соединяющие эти точки (рис. 32). Тогда следующие условия равносильны:
- два произвольных пути (гладкие кривые), соединяющие эти точки (рис. 32). Тогда следующие условия равносильны:
1.  (условие Грина).
(условие Грина).
2. 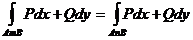 (криволинейный интеграл не зависит от пути интегрирования).
(криволинейный интеграл не зависит от пути интегрирования).
3. 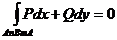 (интеграл по любому замкнутому пути равен нулю).
(интеграл по любому замкнутому пути равен нулю).
4.  (выражение
(выражение  представляет собой полный дифференциал некоторой функции
представляет собой полный дифференциал некоторой функции 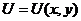 ).
).

Рис. 32.
В случае выполнения любого из равносильных условий теоремы криволинейный интеграл по любой кривой, соединяющей точки  и
и  из области
из области 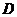 , можно вычислить при помощи формулы Ньютона – Лейбница
, можно вычислить при помощи формулы Ньютона – Лейбница
 ,
,
где 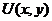 - некоторая первообразная для
- некоторая первообразная для  может быть найдена при помощи криволинейного интеграла
может быть найдена при помощи криволинейного интеграла
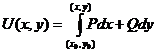 .
.
В этих же условиях на функции 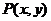 и
и  , а также на область
, а также на область 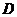 , имеет место формула Грина, позволяющая свести криволинейный интеграл по замкнутому контуру к двойному интегралу
, имеет место формула Грина, позволяющая свести криволинейный интеграл по замкнутому контуру к двойному интегралу
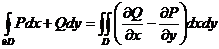 .
.
Считаем, что обход границы  области
области 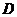 в криволинейном интеграле
в криволинейном интеграле
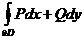
совершается в положительном направлении, т.е. при таком обходе границы область 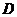 остается слева; для односвязной области это направление совпадает с направлением против часовой стрелки.
остается слева; для односвязной области это направление совпадает с направлением против часовой стрелки.
|
|
Также площадь  области
области 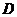 может быть вычислена при помощи криволинейного интеграла второго рода:
может быть вычислена при помощи криволинейного интеграла второго рода:
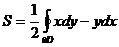 .
.
Пример 1. Даны функции  ,
, 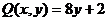 и точки
и точки 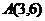 ,
,  ,
, 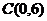 . Вычислить криволинейный интеграл
. Вычислить криволинейный интеграл
 ,
,
где:
1)  - отрезок ОА;
- отрезок ОА;
2)  - ломаная ОВА;
- ломаная ОВА;
3)  - ломаная ОСА;
- ломаная ОСА;
4)  - парабола, симметричная относительно оси
- парабола, симметричная относительно оси 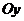 и проходящая через точки О и А;
и проходящая через точки О и А;
5) проверить выполнимость условия Грина.

Рис. 33.
Пути интегрирования, соответствующие пунктам 1) – 4), изображены на рис.33.
1) Отрезок ОА может быть записан в виде:  ,
, 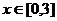 . Тогда
. Тогда 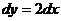 и
и
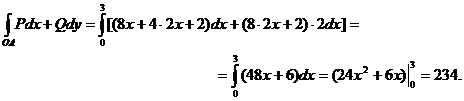 .
.
2) Используем свойство аддитивности, вычисляя отдельно интеграл по отрезкам 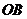 и
и 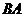 . Тогда:
. Тогда:
а) 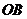 : здесь
: здесь 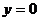 ,
, 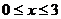 , т.е.
, т.е. 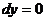 , откуда
, откуда
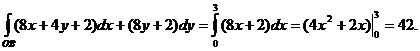
б) 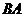 :
:  ,
, 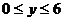 , т. е.
, т. е.  , и
, и

Таким образом,
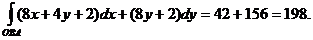
3) Этот интеграл вычислим аналогично предыдущему.
а)  :
: 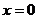 , (т. е.
, (т. е.  ),
), 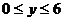 , откуда
, откуда

б) 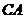 :
: 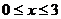 ,
, 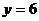 ,
, 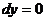 , следовательно,
, следовательно,
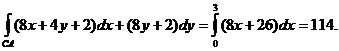
Окончательно
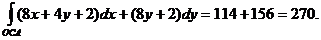
4) Подставим координаты точки 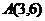 в равенство
в равенство 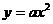 найдем уравнение данной параболы
найдем уравнение данной параболы 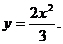 При этом
При этом 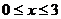 и
и  , откуда (путь ОА по параболе обозначим
, откуда (путь ОА по параболе обозначим 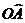 )
)

5) Имеем
 ,
, 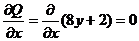 ,
,
т. е. условие Грина не выполняется. Вычисления в пунктах 1) – 3) этой задачи показывают, что данный криволинейный интеграл второго рода зависит от пути интегрирования.
Пример 2. Вычислить интеграл
 ,
,
где  - верхняя половина эллипса
- верхняя половина эллипса 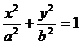 , пробегаемая по ходу часовой стрелки.
, пробегаемая по ходу часовой стрелки.
Воспользуемся параметрическими уравнениями эллипса: 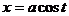 ,
, 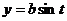 ,
, 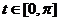 , т. е.
, т. е. 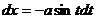 ,
, 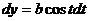 . Подставляя в интеграл и учитывая направление обхода (откуда следует, что
. Подставляя в интеграл и учитывая направление обхода (откуда следует, что 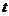 меняется от π до 0), получаем
меняется от π до 0), получаем

Пример 3. Вычислить

по дуге винтовой линии  при изменении
при изменении 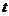 от 0 до
от 0 до 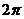 .
.
Сначала найдем дифференциалы переменных:  .
.
Выразим подынтегральное выражение через 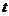 , сводя исходный интеграл к
, сводя исходный интеграл к
определенному:

Пример 4. Показать, что интеграл
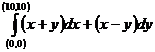
не зависит от пути интегрирования, соединяющего точки 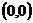 и
и  , и вычислить его.
, и вычислить его.
Проверим условие Грина. Положим  ,
, 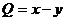 . Тогда
. Тогда 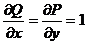 ,и, значит, данный интеграл действительно не зависит от пути интегрирования. Для вычисления данного интеграла в качестве пути интегрирования возьмем отрезок, соединяющий точки O
,и, значит, данный интеграл действительно не зависит от пути интегрирования. Для вычисления данного интеграла в качестве пути интегрирования возьмем отрезок, соединяющий точки O 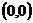 и B
и B  . Отрезок OB можно задать так:
. Отрезок OB можно задать так: 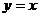 ,
,  . При этом
. При этом 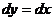 , и интеграл легко сводится к определенному интегралу.
, и интеграл легко сводится к определенному интегралу.
|
|
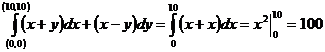 .
.
Пример 5. Вычислить криволинейный интеграл
 ,
,
где L – отрезок, соединяющий точку 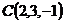 с точкой
с точкой  .
.
Составим параметрические уравнения отрезка CD, используя уравнения прямой, проходящей через две точки:

Отсюда 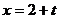 ,
, 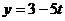 ,
, 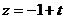 ,
, 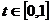 . Далее, находим
. Далее, находим  ,
, 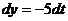 ,
, 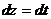 , подставляем все нужные выражения в данный интеграл, обозначенный через J, и вычисляем определенный интеграл:
, подставляем все нужные выражения в данный интеграл, обозначенный через J, и вычисляем определенный интеграл:
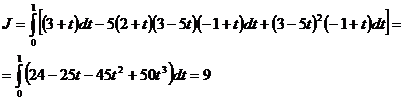
Пример 6. Проверить, является ли выражение

полным дифференциалом некоторой функции 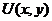 и если да, то найти эту функцию.
и если да, то найти эту функцию.
Обозначим 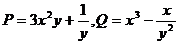 . Тогда
. Тогда
 .
.
Таким образом, условие Грина  имеет место при
имеет место при  .
.
Следовательно, данное выражение есть полный дифференциал некоторой функции 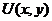 , которая может быть найдена как криволинейный интеграл
, которая может быть найдена как криволинейный интеграл
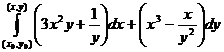 ,
,
где  - произвольная фиксированная точка плоскости
- произвольная фиксированная точка плоскости 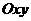 , не лежащая на оси
, не лежащая на оси 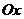 (так как
(так как 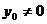 ). Положим
). Положим 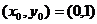 , а в качестве пути интегрирования выберем путь
, а в качестве пути интегрирования выберем путь 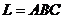 , изображенный на рис. 34.
, изображенный на рис. 34.
Тогда сокращенно можно написать

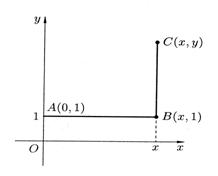
Рис. 34.
Имеем: 1) 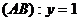 , т.е.
, т.е. 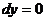 и
и
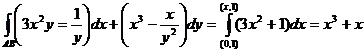 .
.
2) 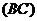 :
: 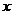 - фиксировано, следовательно,
- фиксировано, следовательно,  , откуда
, откуда
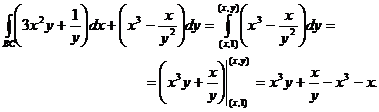
3) Таким образом, 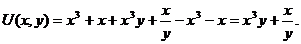
Проверка показывает, что действительно,
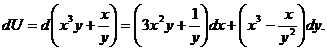
Пример 7. С помощью формулы Грина преобразовать криволинейный интеграл
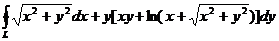
в двойной и с его помощью вычислить интеграл по контуру прямоугольника  (рис.35), где
(рис.35), где  ,
, 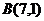 ,
, 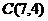 ,
,  .
.

Рис. 35.
Имеем  ,
, 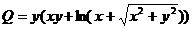 , откуда
, откуда

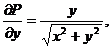
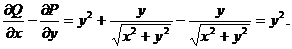
Таким образом, в силу формулы Грина данный интеграл равен двойному интегралу от 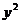 по прямоугольнику
по прямоугольнику  , т. е.
, т. е.
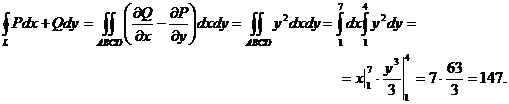
Пример 8. Вычислить площадь эллипса при помощи криволинейного интеграла.
Запишем эллипс 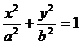 в параметрической форме
в параметрической форме 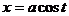 ,
, 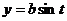 ,
, 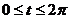 , после чего воспользуемся формулой для площади области
, после чего воспользуемся формулой для площади области 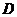
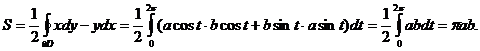
Пример 9. Вычислить работу силового поля F = y i – x j при перемещении материальной точки вдоль верхней половины эллипса
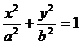
из точки  в точку
в точку 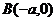 .
.
Работа  силового поля F = P i + Q j при перемещении материальной точки
силового поля F = P i + Q j при перемещении материальной точки 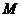 вдоль линии
вдоль линии  равна
равна
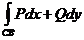 .
.
Запишем дугу эллипса  в параметрической форме:
в параметрической форме: 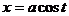 ,
, 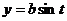 ,
, 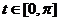 . Тогда
. Тогда 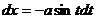 ,
, 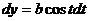 и
и
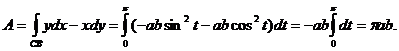
Контрольные вопросы:
1. Дайте определение криволинейного интеграла второго рода от функции 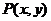 .
.
2. Что называется полным криволинейным интегралом второго рода?
3. Зависит ли криволинейный интеграл второго рода от пути интегрирования?
4. Приведите формулу Грина.
Поверхностный интеграл
|
|
|
|
|

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!