Врезка 9. Как агент ДвОт ловит шпионов.

Обозначим через х, у, t координаты ближайших КП, в районе которых был замечен шпион.

Но тогда надо ответить на два вопроса: где находится нача­ло отсчета, и какая будет единица измерения длины? Ответ: ЭТО НЕ ИГРАЕТ РОЛИ. В самом деле, двойное отношение координат (ДвОт) не изменится, если от всех четырех координат отнять од­но и то же число; оно не изменится также, если все координаты умножить на одно и то же число. Поглядите на формулу ДвОт (формула (5)), и вы сразу поймете, почему это происходит. Итак, давайте запросим координаты точек х, у, t, измеренные в киломе­трах до ближайшей погранзаставы. Допустим, они равны 17, 23, 32 соответственно. А как же мы найдем ДвОт, если «г» нам неиз­вестно? А вот так:

 

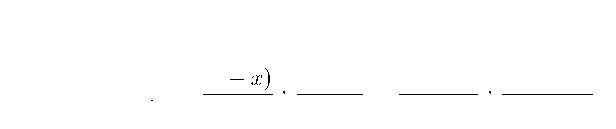
п О = ^ (t‑x) ₌   (z – 17) (32 ‑ 17)

 

Приравнивая буквенное выражение ДвОт к его числовому выра­жению, получаем уравнение первой степени для нахождения «г»:

^{АВ Т} (z‑y)'(t‑y) (z – 23) ’ (32 – 23) ’

А теперь внимательно изучим кадр аэрофотосъемки, где бы­ли зарегистрированы три КП и один Ш (шпион). Их координаты будем выражать в миллиметрах, а первое КП будем считать на­чалом отсчета (для простоты). Обозначим эти четыре координаты за А, Б, С, Д (где, как мы решили, А = 0). Прочие (ненулевые) координаты мы просто измеряем с помощью миллиметровой ли­нейки, приложенной к фотоснимку. Допустим, мы получили числа (0, 13 мм, 16 мм, 31 мм). Следовательно, мы можем найти ДвОт уже не в виде формулы, а в виде числа:

тт п ‑ (¹⁶^°) (³¹^°) _ о П07

 

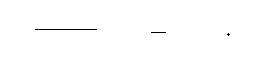
^{Дв Т} (16 ‑ 13) ' (31 ‑13) ’ '

 

Ј ~ 17. JL _ з Qgj

г ^23 15 ’

Отсюда получаем г и 24,4 км.

После чего агент ДвОт сообщает начальнику погранзаставы, что подозрительного человека имеет смысл поискать на рассто­янии 24 км и 400 м от заставы. Где он и был найден спящим под кустом, чтобы, дождавшись ночи, начать свою деятельность.

Свойства ДвОт станут понятнее, если рассмотреть следующий пример (рис. 113).

Здесь производится «одномерная» фотосъемка линии ORST из точки К на «линию кадра» OMNL. Конечно, в реальной ситуации будет не линия, а плоскость кадра, и лежать она будет значитель­но ближе к точке К. Но суть дальнейшего исследования можно изложить и на таком условном рисунке.

 

Рис. ИЗ. Изображен прямоугольный равнобедренный треугольник КОТ. Длина катета равна 4 единицы. Из прямого угла опущена высота OL на гипотенузу. Из верхней вершины треугольника К проведены две пунк­тирные линии KR и KS, делящие основание на отрезочки длиной 1.

и 2 ед. Основание треугольника лежит на плоскости, которую фото­графирует самолет (рис. 111). вершина К местоположение самолета, а высота OL лежит в плоскости, в которой находится кадр фотоплен­ки (вторая плоскость случайно может оказаться параллельной первой; но гораздо чаще этого не случается). Точки пересечения линий KR и KS с высотой 0L обозначены за М и N соответственно. Длины отрезков

ОМ, MN, NK равны 6а. 4а. 5а соответственно, где а = (для

полноты картины!).

Прежде всего отметим, что если бы линия кадра была парал­лельна фотографируемой линии, то соотношение расстояний ме­жду точками 0. R. S. Т и точками 0. М. N. L было бы одинаковым (и равным 1: 1: 2). и никакого «двойного отношения» нам бы не понадобилось.

В случае же, когда параллельности плоскостей нет. произойдет искажение этого соотношения.

Вычислим, насколько сильным оно будет. Уравнения прямых KR. KS легко получить по формуле «уравнение в отрезках»:

+ 1 = 1 (KR) и ^ + ^ = 1 (KS).24 Уравнение же высоты и того проще – оно имеет вид «у = ж».

Поэтому мы легко находим координаты точек Л/. N: М( 4/5,4/5) и iV(4/3,4/3), а также обычное тройное отношение от­резков ОМ: Л / N: NL = 6:4:5 (а не 1:1:2, как было «на мест­ности»), Можно теперь ввести координаты на прямой OL таким образом, что точка М получит координату 6, точка N координату 10, а точка L координату 15. При этом поменяется масштаб, но он на двойное отношение четырех точек влияния не оказывает.

Теперь мы убедимся, что «ДвОты» для точек О, R, S, Т и для точек О, М, N, L будут СОВПАДАТЬ, несмотря на то, что обыч­ные отношения для них не совпали.

В самом деле, для точек О, R, S, Т ДвОт =

Для точек же О, М, N, L ДвОт = ^^ ^

* *

Теперь второй сюжет: построения циркулем и линейкой.

(В 11 классе я на экзамене по геометрии получил такое зада­ние, что даже и циркулем пользоваться было нельзя. Третий сю­жет, который мы рассмотрим, – это построение одной линейкой. Циркуль отменяется. Есть только линейка. Здесь всё еще веселее. Я расскажу про одну конкретную очень красивую задачу. Но об этом – ниже.)

Помните ли вы о построениях циркулем и линейкой? Построе­ния циркулем и линейкой выводят на весьма сложные математи­ческие закономерности. Что мы умеем строить циркулем и линей­кой? Можно, например, построить равнобедренный треугольник, если известны длина основания и длина боковой стороны.

Ну, скажем, основание 10 см, а боковые стороны – по 13 см. Линейкой проводим любую прямую, циркулем делаем на ней в лю­бом месте засечку. Циркулем же измеряем основание (10 см) и де­лаем па прямой вторую засечку, предварительно установив иглу циркуля в первую. Берем раствор циркуля равным длине боковой стороны (13 см) и ставим иглу циркуля сначала на левый край основания, проводя достаточно длинную дугу в верхней полуплос­кости, а затем на правый край (и проводим дугу до пересече­ния с первой дугой). Взяв линейку, соединяем точку пересечения дуг сначала с левой точкой основания, а потом с правой (см. рис. 114).

 

Рис. 114‑ Построение равнобедренного треугольника с помощью циркуля и линейки.

В общем, всё это быстрее сделать, чем описывать. Если Вы уста­ли, вот вам задачка. Один школьник перепутал, что такое 10 см основание или боковая сторона. И из‑за этого построил не тот тре­угольник, что было нужно. Как вы думаете, что сильнее искази­лось (в процентах) из‑за рассеянности: площадь треугольника или его периметр? (Ответ: площадь изменилась больше, чем на 15 про­центов, а периметр менее, чем на 10 процентов.)

Можно построить квадрат. А вот можно ли построить пра­вильный пятиугольник с данной стороной? Это не очень про­сто. Но можно. Пифагорейцы уже умели строить правильный пя­тиугольник. Правильный шестиугольник построить совсем про­сто: строю окружность с радиусом, равным заданной стороне 6‑ угольника. Теперь делаю подряд 6 засечек на окружности окруж­ностью того же радиуса. О чудо, шестая попадает прямо в то место, откуда мы начали. Так уж вышло! Далее прикладываем линейку к первым двум засечкам и проводим отрезок, их соединяющий. Потом то же делаем для следующих двух засечек, и т. д., пока не получим все 6 сторон шестиугольника (см. рис. 115). Итак, пра­вильный шестиугольник построить просто. Треугольник триви­ально. квадрат очень просто, пятиугольник сложно, но можно. Вопрос. Можно ли построить правильный семиугольник? Древние сломали миллион копий в спорах и потратили кучу часов, пытаясь решить эту задачу, но решена она была только в XIX веке!

 

На самом доле, кроме этой задачи, древние оставили нам еще три известные проблемы.

Трисекция угла. Дан какой‑то угол на плоскости. Надо раз­делить его на три равные части. Знаменитая проблема древних; примерно в том же начале XIX века было доказано, что трисек­ция угла с помощью циркуля и линейки невозможна.

Квадратура круга. Что значит «квадратура круга»? Дан круг. Нужно построить квадрат с такой же площадью. Пусть радиус круга г равен единице, тогда его площадь S равна 7г (по формуле S = 7гг²). Значит, нужно построить квадрат со стороной, равной т/ж. Эта задача эквивалентна задаче построения числа ж. которая тоже была решена (в отрицательном смысле), но только в конце XIX века. Почему она была решена позже, чем другие задачи, оста­вленные нам древними? Потому что люди очень долго не понимали структуру числа тт. В начале XIX века было доказано, что можно построить те и только те точки плоскости, у которых обе коорди­наты могут быть получены из единицы за конечное число опера­ций плюс, минус, умножить, разделить, взять квадратный корень. Берете единицу. Вам разрешается ее складывать с самой собой. Так получатся все натуральные числа. Если будете вычитать все отрицательные. Рассмотрим дроби. Дроби математики назы­вают специальным термином рациональные числа. То есть это

числа, которые представляются в виде «целое делить на целое».

Например, число 2 рациональное, так как может быть пред‑

4

 

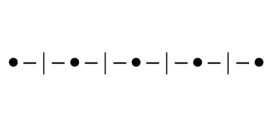
Рис. 116. Изображение чисел вида при п = 2. Если т четно, полу­чаются целые числа (обозначены кружками). Все прочие числа такого вида изображены вертикальной черточкой.

ставлено, как у или То есть все целые числа также являются рациональными. Давайте посмотрим, где будут жить точки «целое число пополам». Во‑первых, будут жить в целых, потому что лю­бое целое, это как бы «удвоенное целое пополам». Во‑вторых, они будут жить посередине между соседними целыми (рис. 116).

 

‑0,5 0,5 1,5 2,5

 

‑10 12 3

А если я еще раз разделю пополам? Я могу нарисовать, где жи­вут числа, полученные из целых делением на 3, на 5, на 1000 и т. д. Но удивительным фактом, который был известен уже древним, является то, что не все числа можно представить в виде дроби. Например, я построю квадрат со стороной 1 и возьму его диаго­наль. Ни одна обыкновенная дробь не равна длине диагонали ква­драта. Заметьте, что число, равное диагонали квадрата, строится циркулем и линейкой (так как сам квадрат циркулем и линейкой мы построить можем).

Но оно не является рациональным числом. Это было помещено в первой части книги. То есть мы умеем теперь строить квадратные корни, потому что диагональ квадрата выражается квадратным корнем.

Любое рациональное число можно построить циркулем и линей‑

11

кой. Давайте, например, построим –Знак минус просто означа­ет. что число надо откладывать не вправо от нуля, а влево. Чтобы

1 построить достаточно построить ^ и отложить этот отрезок

раз. А чтобы построить у. придется использовать очень удоб­ную: теорему Фалеса (которая изучается в школе). Сейчас мы ею воспользуемся.

 

Теорема Фалеса (в простейшей формулировке). Если на одной из двух прямых в плоскости отложить последователь­но несколько равных отрезков и через их концы провести парал­лельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки (рис. 117).

 

Рис. 117. Дво прямые (горизонтальная и наклонная) выходят из начала координат и поросочоны системой параллельных прямых. Если на одной из прямых мы отсекли равные отрезки, то на другой прямой отрезки тоже будут равны между собой (Теорема Фалеса).

Мне дан единичный отрезок. Отложу его по горизонтальной оси от начала координат и проведу произвольную наклонную прямую (тоже из начала координат) (рис. 117).

На этой прямой отложу от начала семь равных отрезков (не­важно. какой длины) и конец последнего отрезка соединю с концом единичного (горизонтального) отрезка.

После этого провожу прямые, параллельные той. что соединила концы горизонтального (единичного) отрезка и наклонного отрез­ка. и проходящие через конец предпоследнего из семи отрезков; затем через конец пред‑предпоследнего. и так далее.

По теореме Фалеса получается, что все получившиеся на гори­зонтальном единичном отрезке кусочки равны друг другу то

1

есть мы получили

Корень строится немножко сложнее. Беру произвольное число

а, которое я уже построил циркулем и линейкой и из которого

 

Рис. 118. Отрезок и = 5 отложен между х = –3 и х = 2; единичный отре­зок между х = 2 и х = 3. Строим полуокружность радиуса 3. Проводим перпендикуляр из точки х = 2 до точки пересечения с окружностью. Это и есть отрезок длины \/5. Все три треугольника прямоугольные, и все они подобны друг другу.

Теперь я рассматриваю новый отрезок длины а + 1 как диаметр окружности. Делю его пополам (это мы делать умеем) и строю верхнюю полуокружность.

Из точки х = 2 (отделяющей отрезок «а» от отрезка 1) восста­навливаю перпендикуляр. Получаю отрезок с концами на окруж­ности и отрезке.

 

Теорема: длина полученного отрезка равна \/5.

Доказательство. Обозначим за А и В концы диаметра, за М и С концы проведенного нами перпендикуляра (С ниже, чем М). Треугольник АВМ подобен треугольнику AM С, так как у них острые углы совпадают, а один из углов прямой. (Угол АМВ прямой, как и любой угол, вписанный в полуокружность.) Значит, и третьи углы равны. По той же причине и треугольник АВМ подобен треугольнику МВС. Значит, можно записать отношение катетов малых треугольников

_ х

 

х а

(где «ж» – длина проведенного нами перпендикуляра); ж² = а, ж = л/а, что и требовалось доказать.

Теперь мы умеем строить всякие страшные «многоэтажные че­моданы». Любое выражение, которое является результатом конеч­ного числа операций плюс, минус, умножить, делить и взять ква­дратный корень, можно построить циркулем и линейкой. Напри­мер,