Врезка 2. Эйнштейн – о топологии

Однажды А. Эйнштейна попросили совсем кратко, на понятном любому языке, пояснить, в чем состоит суть сделанных им откры­тий. Он ответил: все мы, люди, словно маленькие жучки с завя­занными глазами, ползающие но поверхности большого мяча и во­ображающие, что двигаемся но плоскости. Я же первый понял, что мир, в котором я живу, искривлен. Но пока не совсем понятно, как именно он искривлен. (То есть, «по‑научному», каков топологиче­ский тип космоса.)

А вот к чему. Несколько лет назад математик Г. Перельман установил похожий факт, но только в пространстве больших из­мерений. Факт про фигуры в многомерном пространстве, которые локально похожи на искривленное трехмерное пространство. Мы живом в трехмерном пространстве, мы четвертого измерения не ви­дим и не чувствуем. Мы можем только рассуждать, что четвертое измерение это время, но объять его взором не можем. Поэто­му мы не можем говорить так спокойно и убежденно, что сделать из шара тор в пространстве больших измерений нельзя. (Ведь в 4­мерном пространстве, как указывалось выше, МОЖНО, не нару­шая правил топологии, превратить незаметным образом человека с сердцем, расположенным слева, в человека с сердцем, располо­женным справа.)

Нам нужен язык, на котором это можно доказать. И вот для то­го, чтобы это можно было доказывать, для того чтобы через много лет Перельман смог доказать «гипотезу Пуанкаре» (после того как ее доказали, она вместо гипотезы Пуанкаре стала называться те­оремой Перельмана или Пуанкаре Перельмана), Эйлер начал большой путь. Он перевел то, что мы с вами считаем очевидным, в точное, железобетонное математическое рассуждение. Как же он это сделал? Он нарисовал на поверхности шара, мяча, арбуза, гло­буса, любого круглого объекта некоторую карту. Иными словами, некий искривленный многогранник (рис. 29).

 

С точки зрения топологии, любой многогранник это тоже шар. Тетраэдр это шар. куб это шар. октаэдр, любой парал­лелепипед это всё шары. Например, потому что если их выпол­нить из резины и надуть, то получится футбольный мяч. то есть шар. Но до работ Эйлера еще не было «точки зрения топологии», так как не было и самой топологии.

Эйлер «чувствовал», что все эти объекты одинаковые. В чём именно? И как это объяснить остальным людям? В особенности его интересовал вопрос: как доказать, что поверхность шара, по­верхность бублика, поверхность кренделя неодинаковые?8 В ответ на первый вопрос ясность позже внес Анри Пуанкаре (после то­го, как Огюст Коши внес должную ясность в вопрос, что такое «непрерывная функция»). Однако Эйлер сразу обратился ко вто­рой задаче (о доказательстве неодинаковости двух поверхностей) и блестяще решил ее.

Эйлер сделал следующее. Он нанес на поверхность шара мно­гогранник картиночку «стран», причем страны необязательно треугольные (рис. 30). (Если говорить о «странах», то надо по­мнить, что рассматривается «Земной шар», не содержащий морей и океанов.) При этом вся поверхность шара должна быть покрыта многоугольниками.

 

Главное, чтобы каждая страна была простым плоским объек­том, без дырочек, как круг или квадрат. И далее он сделал то же самое с велосипедной камерой. Нанес такой многогранник, ко­торый является как бы «остовом» каретного колеса (машинных колес в то время еще не было!). При этом вовсе не обязательно, чтобы количество и вид граней, а также количество вершин и ре­бер этого многогранника для шара и для колеса были одинаковы.

Более того, они и не могут быть одинаковыми (как мы увидим ниже).

А потом стал считать у этих многогранников эйлерову харак­теристику: величину В – Р + Г.

Число вершин минус число ребер плюс число граней. Как бы мы ни мяли и ни изгибали шар, наши грани – «страны» от это­го не меняются. (Но, конечно, нельзя так смять страну, чтобы она вся превратилась в отрезок. Такого даже во время наполеоновских войн не происходило! А если говорить серьезно, то отрезок – од­номерный объект, а страна – двумерный.) То есть вершины оста­ются вершинами, ребра – ребрами, а грани – какими были (на­пример, изогнутым пятиугольником или треугольником), такими и остались. А значит, величина В – Р + Г не меняется. Теперь счи­таем эту величину на колесе (по науке поверхность колеса (или бублика) называется словом «ТОР». А тор, заполненный внутри, называется полнот,орием. Поверхность же шара называется, как известно, сферой). И если сфера может перейти в тор, то картинка на шаре перейдет в картинку на колесе. И, значит, их эйлерова характеристика должна быть одинакова.

Докажем, однако, что у любой фигуры, нарисованной на колесе, эйлерова характеристика равна 0, а у любой фигуры на шаре – равна 2.

Слушатель: А если бы получилась одна и та же цифра, то что?

А.С.: Мы не смогли бы сделать из этого никакого вывода. Мы бы не смогли сделать вывод, что они одинаковые, но не смогли бы сделать и вывод, что они разные. Но ведь есть и другие подходы, кроме формулы Эйлера. Для более сложных случаев.

 

Слушатель: Понятно.

Слушатель: А как взаимосвязаны картинки на торе и шаре?

А.С.: То есть как именно они друг с другом соотносятся? Ни­как. Каждая из картинок, независимо друг от друга, является как бы «сетью», наброшенной на данную поверхность. Эту сеть при же­лании можно сделать состоящей из треугольных ячеек. Тогда она называется «триангуляцией поверхности».

Слушатель: А не может быть такого, что будет то же самое количество вершин, ребер и граней, но при этом картинка будет другая?

А.С.: Смотря, что понимать под словом «другая». Она может, безусловно, немного иначе выглядеть: ребра могут быть длиннее или короче. Но мне достаточно того, чтобы имелось то же самое количество вершин, ребер и граней. А при изгибах, растяжениях и сжатиях поверхности это будет именно так.

 

Слушатель: А...

А.С.: Итак, если вы поверили, что не изменится ни количе­ство вершин, ни количество ребер, ни количество граней, то всё остальное я докажу совершенно строго. Я продемонстрирую, что величина В – Р + Г на шаре и на торе разная: на автомобильной камере она равна 0, на сфере – равна 2.

Слушатель: А если предположить, что дырка у тора имеет площадь ноль. По‑прежнему число Эйлера – О?

А.С.: А что значит «площадь дырки»? Это значит, что бублик сходится в одной точке – в серединке?

 

Слушатель: Да.

А.С.: Нет, эйлеров индекс В^Р + Г будет другой. Фигура, кото­рая получится, не устроена как обычная плоскость в окрестности любой своей точки, потому что в окрестности серединки, где дырка сходится с разных сторон, она устроена очень сложно.

Чтобы понять это, рассмотрим сечение тора (с заклеенной ды­рой) вертикальной плоскостью, проходящей в стороне от точки за­клейки, а также плоскостью, проходящей через точку заклейки. Рассмотрим две замкнутые кривые, получившиеся в сечениях (см. рис. 31).

Первая кривая устроена как окружность, окрестность любой ее точки – просто интервал, а вторая кривая устроена иначе (рис. 32). Потому что в любой микроскоп окрестность точки пе­ресечения видится как крест, а не как отрезок. То же самое с то­ром – с автомобильной камерой. С точки зрения таракана, кото­рый по ней ползает, это просто плоскость (если, конечно, дырка

 

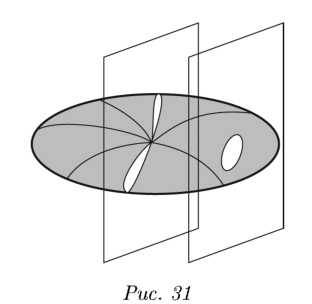
в торе но была заклеена). Но и шар с точки зрения таракана тоже плоскость (ведь он в каждый момент времени видит только маленький кусочек «у себя под носом», а он почти плоский). То есть смотрите, что происходит. Таракан, который ползает по то­ру и по шару, не может понять, что это разные объекты. Мы та­кие же тараканы, мы живем в трехмерном пространстве, мы трехмерные тараканы. Мы знаем, что вокруг нас есть окрестность. Окрестность это обычное трехмерное пространство: его опреде­ляют 3 взаимно перпендикулярных оси. То есть я вижу трехмер­ную окрестность вокруг себя, но я не знаю, как устроена вся все­ленная целиком. Я не могу иметь такого представления. Так вот: топология приоткрыла эту тайну. Гипотеза Пуанкаре как раз про то. как устроено пространство, где мы живем. Мы видим, что во­круг нас всё трехмерно, но мы не знаем внутри какого рода объекта мы живем. То ли мы живем в обычном бесконечном трехмерном пространстве, то ли мы живем на поверхности трехмерной, изви­ните. сферы, которая ограничивает четырехмерный шар. Не мо­жем мы этого понять, просто посмотрев вокруг себя. Ведь радиус такой «трехмерной сферы» может равняться, скажем. 100 милли­онам световых лет. А на такие расстояния глаз посмотреть не спо­собен.

 

 

Врезка 3. Еще одно упражнение для слушателей. Ниже описано странное путешествие неких космических Магел­ланов. Могло ли такое быть в космосе?

... Вех; астрономы Земли в 3333 году нашей эры были в глубо­ком недоумении. Один из них. направляя свой телескоп в разные точки небесной сферы, имел привычку фотографировать не толь­ко ее. но и (перейдя в другое полушарие Земли), фотографировать также диаметрально противоположную ей точку. Накопив изряд­ное количество таких пар фотографий, он принялся их изучать. И вдруг сюрприз: на одной из двух фотографий пары он увидел маленькое, но вполне различимое созвездие в виде правильного пя­тиугольника. Велико же было его изумление, когда на другой фо­тографии пары он увидел ТАКОЕ ЖЕ созвездие, той же величины и той же яркости! Велико было и удивление всех остальных астро­номов. когда они услышали это сообщение (и немедленно провери­ли его). И скоро об этом узнали все жители Земли. Было решено одновременно выслать две космических экспедиции (на предмет проверки, не посылают ли на Землю сигналы внеземные цивили­зации): одна экспедиция – прямо в центр первого пятиугольника, вторая – в центр диаметрально противоположного пятиугольни­ка.

Долго летели космонавты в ту и в другую сторону с одинаковой «субсветовой» скоростью – целых 10 лет. И всё это время за их ракетами наблюдали чуткие приборы астрономов. Вдруг в центре первого 5‑угольного созвездия была зафиксирована яркая вспыш­ка неправильной формы, и первая ракета ИСЧЕЗЛА. Астрономы решили взглянуть, видна ли вторая ракета. К своему ужасу, они увидели, что ровно в тот же момент с диаметрально противопо­ложной стороны была зафиксирована вспышка ТОЙ ЖЕ ФОРМЫ, и вторая ракета тоже исчезла.

Могло ли такое быть?

 

ОТВЕТ. Могло. Если бы только космос, в кот,орый погружена Земля, был не бесконечным трехмерным пространством, а очень большой, по конечной трехмерной сферой.

Чтобы лучше понять это, представьте себе, что наша Земля сплошь покрыта мировым океаном, на котором имеется (на эква­торе) только один небольшой остров вроде Крита. Поверхность этого океана является двумерной сферой, но свойства у нее по­хожи на свойства трехмерной сферы. И выплыли с этого острова два одинаковых корабля (в один и тот же момент времени): один поплыл ровно на запад, другой – ровно на восток. Плыли они быстро и потому очень сильно столкнулись (в точке, диаметраль­но противоположной острову Криту). От столкновения они могли взорваться. После отплытия прочие люди следили за ними, посы­лая вслед радиоволны (а они, как известно, могут огибать поверх­ность Земли). На экране радара и на западе, и на востоке всё вре­мя был виден какой‑то странный правильный пятиугольник (ока­залось, что это – радиомаяк из пяти источников, построенный кем‑то на противоположной точке поверхности Земли). Корабли взорвались как раз в центре этого пятиугольника. Взрыв был за­фиксирован одновременно и западным, и восточным радаром.

Сверху из нашего трехмерного мира мы видим, что тор и сфе­ра – разные объекты. Но глазами червя, который ползает по дву­мерной поверхности, этого не видно, всё одинаковое. Вопрос: как же доказать червю, что поверхности разные?

Допустим, что у червя есть мышление, он может воспринять ма­тематическое рассуждение. Как я могу передать ему знание? А вот как. Я ему говорю: «Ты можешь, экспериментально исползав сфе­ру, проверить, сколько здесь вершин?» Он говорит: «Ну, конечно могу. Я постепенно все их обползаю, поставлю метку, найду алго­ритм, которым я посчитаю количество вершин». Тогда я спрошу: «Можешь ли ты посчитать количество ребер?» – «Ну, конечно, могу», – говорит он. «А граней?» – «Тоже могу. Нет проблем ни­каких. Каждый раз переходя из грани в грань, заливаю ее водой. В следующий раз я к ней приду, а она уже мокрая, значит, я ее уже посчитал». Понятно, что, находясь на двумерной поверхности, не выходя в трехмерное пространство, можно посчитать, сколько ребер, вершин и граней. Теперь, если я пересажу червя на тор, он посчитает вершины, грани и ребра и убедится, что индекс Эй­лера имеет другое значение. На сфере – 2, а на торе – 0. Тут я ему и скажу: «Теперь ты понимаешь, что поверхности абсолют­но разные, они с нашей человеческой трехмерной точки зрения абсолютно разные. Они с твоей точки зрения одинаковые, потому что ты видишь локально, а с нашей трехмерной – они разные». То же самое происходит с нашей трехмерной вселенной, с точки зрения четырехмерного пространства. Наше пространство может быть устроено по‑разному, но Г. Перельман доказал теорему, ко­торая ограничивает класс того, что нам нужно проверять, когда мы выясняем, где живем.

Слушатель: А как Эйлер пришел именно к этой формуле?

А.С.: Честно говоря, я не знаю, но он вообще был гений. Го­ворят, что у него никогда не было математических ошибок и не­верных утверждений. Даже не совсем обоснованные рассуждения Эйлера (после их очевидной коррекции) были впоследствии под­тверждены. Видимо, он настолько верно чувствовал ситуацию, как будто внутри него находился «барометр правильности», с которым он постоянно сверялся.

Математика это прозрение. Вы идете но парку, вокруг листья шелестят, бах и вы всё поняли. Это не от вас, это как бы сверху идет.

Сейчас я буду доказывать, что на сфере индекс Эйлера равен

а на торе он равен 0, и, может быть, вам будет ясно, как Эйлер к этому пришел.

 

Рис. 33. Накидываем «сеть» из ребер и вершин на верхнюю половину сферы и на небольшой кусок поверхности тора. Нижняя часть сферы может трактоваться как одна гигантская грань (грани не обязательно должны быть треугольными). Оставшийся кусок тора НЕ МОЖЕТ счи­таться «гранью», так как грань не может выглядеть как трубка. Надо эту трубку подразбить на более мелкие части (на треугольники, квадратики и т.д.).

Допустим, я уже сформировал «сеть», покрывающую сферу, и «сеть» для тора (рис. 33).

Стираю одно ребро на сфере (потом буду стирать ребра и на то­ре). Что меняется вот в этом нашем выражении (то есть В^Р + Г)?

Слушатель: Минус одно ребро.

Слушатель: Минус одна грань.

А.С.: Значит, выражение В – Р + Г не изменилось (рис. 34).

Какие еще операции я могу сделать с этой картинкой? Могу убрать еще одно ребро. Опять ничего не изменится. Но в какой‑то

 

момент меня ударят но рукам. Некоторые вершины могут стать странными (что‑то вроде куска забора в чистом поле).

Может получиться «висячая вершина» она связана с един­ственным ребром (может быть и несколько таких кусков, см. рис. 35).

 

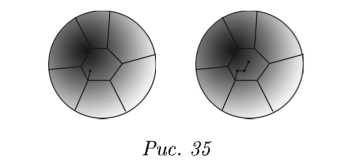
Давайте превратим вот такое ребро во что‑нибудь человеческое (только не в человеческое ребро!). Что для этого надо сделать?

 

Слушатель: Выпрямить.

А.С.: Да. Удалить вершину и выпрямить границу, убрав ненуж­ный «кусок границы». Что изменилось?

Слушатель: Минус вершина.

Слушатель: Минус ребро.

А.С.: Минус ребро, потому что из двух соседних ребер стало одно. Заметьте, что в выражении В – Р + Г опять ничего не изме­нилось. Итак, я буду упрощать картинку дальше (см. рис. 36).

Что происходит, когда я сниму еще ребро?

Пусть возникнет еще одна аномалия такого же типа. Возник­нет вершина, из которой торчит ребро, и на другом конце ребра висит пустая вершина. Но по‑прежнему В – Р + Г такое же. как было раньше. Что я теперь могу сделать с этой вершиной и этим

 

ребром? Стереть их целиком. При этом количество и вершин, и ре­бер уменьшится на 1 (рис. 36). Значит, выражение опять не изме­нилось. а «сеть» на поверхности стала проще.

Я значительно увеличил грань, я убрал всё внутри нее. а вы­ражение не менялось. «Сеть» свелась к двум граням, охваты­вающим сферу «сверху и снизу», разделенным замкнутой лома­ной; в ней количество вершин равно количеству ребер, то есть В^Р + Г = Г = 2.

Для сферы формула Эйлера тем самым доказана.

Вопрос: «В какой ситуации логика этих рассуждений не мо­жет быть проведена?» Математик всегда изучает, в каком месте его рассуждение не пройдет. А не пройдет оно. например, на торе. На торе берем вершину и 2 ребра (рис. 37).

 

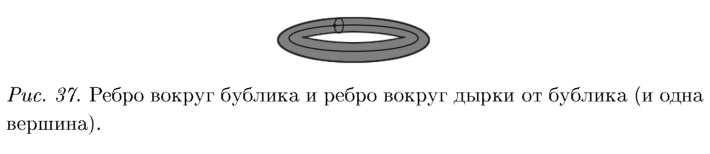
К такой картинке (рис. 37) приводится сниманием ребер любая «сеть» (достаточно общего вида) на торе. Почему же нельзя снять еще одно ребро? Здесь я взываю к интуиции слушателей. Если мы разрежем тор по этим ребрам, а потом развернем, то получим квадрат. Чтобы лучше себе всё это представить, проделаем данные операции в обратном порядке: возьмем обычный квадрат из гибкой резины и изогнем его так. чтобы две противоположные стороны квадрата совпали (и затем склеим по совпавшим сторонам).

Получилась трубка (две оставшиеся стороны квадрата превра­тились при этом в два колечка). Изогнем трубку таким образом, чтобы эти колечки тоже совпали (и склеим их). Вот и получился из квадрата тор. По местам склеек восстанавливаем, где на этом торе расположены два ребра и одна вершина (из четырех вершин квадрата получилась ОДНА вершина на торе).

Осталось пояснить только один важный вопрос: так все‑таки можно или нельзя при изучении топологии делать склейки, раз­рывы и надрезы? Выше говорилось, что при этом может изменить­ся топологический тип объекта. Значит, если мы хотим сохранить топологический тип объекта, этого делать нельзя. Но можно без­болезненно делать многое другое: растяжение, сжатие, перемеще­ние, поворот объекта, увеличение его в несколько раз. Эти опе­рации позволяют представить изучаемый объект в самом простом для понимания виде. Например, конус (заполненный внутри) мож­но превратить в шар.

Однако, если мы хотим изменить топологический тип, то мож­но (и даже нужно) делать разрезы и склейки. Эти операции так часто применяются в топологии, что даже носят специальное на­звание: «топологическая хирургия». Более того, практически лю­бой интересный для изучения объект можно склеить из весьма простых кусков. Скажем, торическую поверхность можно полу­чить склейкой нескольких треугольных кусков. А когда склейка будет закончена, места склеек будут определять некоторую «сеть» на торе. «Сеть», составленная из треугольников (естественно, кри­волинейных), называется «триангуляцией». Простейшая «сеть» на торе (рис. 37) не является триангуляцией, так как она полу­чена не из треугольников, а из квадратов... точнее, из одного‑ единственного квадрата. Но этой беде легко помочь: когда мы вы­ше делали операции в обратном порядке, надо было на исходном квадрате нарисовать диагональ (то есть вместо квадрата далее рассматриваются «два склеенных треугольника»). После двух вы­шеописанных склеек из этого квадрата получится триангуляция тора. Она состоит (хотя в это и трудно поверить) из двух граней, трех ребер и одной вершины (к которой подходят все шесть концов этих трех ребер!).

Можно порекомендовать слушателям купить свежеиспеченный бублик с маком и. прежде чем его съесть, внимательно осмотреть и понять, как именно проходят но его поверхности ребра данной триангуляции. Но специалист‑тополог может представить себе эту триангуляцию даже с закрытыми глазами!

Проверьте, возьмите любую ненужную велосипедную камеру, разрежьте и попытайтесь развернуть. Сохранится тот факт, что грань выглядит как квадрат или как круг, то есть она. как говорят математики. :топологически ·тривиальна. Она выглядит почти как обычная плоская фигура. А вот если мы снимем ребро (т. е. сотрем его с поверхности тора) и потом разрежем по оставшемуся ребру, у нас возникнет нетривиальная фигура в виде кольца. (Кстати, слово «тривиальный» восходит к слову «тривиум», обозначающе­му начальный уровень образования в средневековых университе­тах.)

Колечко на плоскости (рис. 38) не является топологически три­виальным. у него внутри дырка. Получается, что нам запрещено убирать это ребро, потому что мы изменим тривиальный объект на нетривиальный. Математика прошла долгий путь, прежде чем смогла понять, чем формально квадрат отличается от кольца.

 

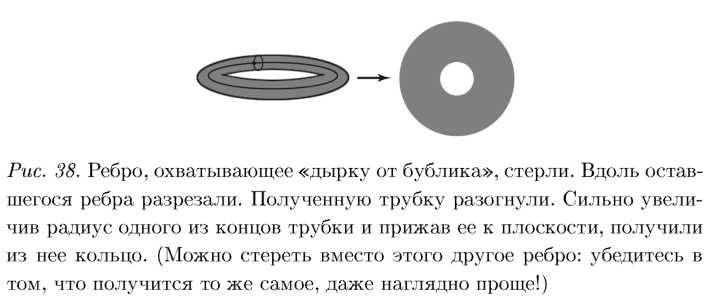
Но если мы примем к сведению этот путь, то сможем воспользо­ваться его результатами. Сможем сказать, что можно снимать ре­бро тогда и только тогда, когда объект, который возникает, будет топологически тривиален, то есть будет похож на квадрат но сво­ей топологической структуре. Именно поэтому я не имею нрава стирать на торе ребро.

Итак, чему равно В^Р+Г для нашей картинки (рис. 38)? Сколь­ко у нас вершин?

 

Слушатели: Одна.

А.С.: Граней?

 

Слушатель: 4?

А.С.: Нет, одна грань. Эта одна и та же грань. Посмотрите, из любой точки грани я могу пройти в любую другую, не пересекая рёбра. А это значит, что грань одна.

На торе сейчас всего одна грань, одна вершинка и два ребра. Поэтому В – Р + Г = 0.

И всегда для тора будет ноль.

А к чему я приду на сфере, когда сниму все возможные ре­бра и вершины? Какой объект получится? (То есть мы не хотим останавливаться на сети в виде двух граней, охватывающих сферу сверху и снизу, как выше, а хотим сделать ее еще проще.) Я утвер­ждаю, что в итоге останется просто голая сфера с одной вершиной. Все ребра будут сняты.

Слушатель: И как получится два?

А.С.: Вот как. У вас одна вершина, одна грань и ноль ребер.

Почему я не могу снять и точку тоже? Потому что, если я ее сниму, останется сфера, которая топологически не похожа на ква‑

 

– 0 + 1 = 2 (см. рис. 39).

драт. А вот, если я сферу проколол... Что происходит с камерой мяча, который проткнули иголкой? Ои сдувается и превращается (если сильно увеличить место прокола и наложить на плоскость) в лоскут в плоскую фигуру. Сфера отличается от плоского кус­ка только одной точкой. Очень хорошо это понимают грузины, бу­ряты и тувинцы. Они делают большие пельмени (хинкали. позы и буузы).

 

Как их делают? Берут кусок теста, поднимают за края, слепля­ют, и получается сфера. Так что в топологии можно сказать, что сфера отличается от круга всего одной точечкой. Отсюда и возни­кает одна точка и ноль ребер.

Давайте к одной вершине добавим одно ребро (рис. 40). Что изменилось? Добавилось одно ребро и одна грань. То есть у нас одна вершина, одно ребро и две грани. Странно смотрится замкну­тое ребро на рис. 40? Давайте тогда поставим еще одну вершину (рис. 41).

 

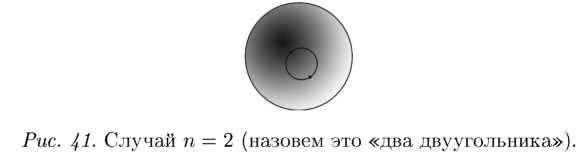
Итак: 2 вершины. 2 ребра. 2 грани: 2 – 2 + 2 = 2.

Не бывает двугранников? Да еще образованных двумя «дву­угольниками»? Хорошо. Чтоб не было сомнений, добавим еще две вершинки. Получится квадрат на сфере, то есть п = 4.

 

4 вершины, 4 ребра, 2 грани: 4 – 4 + 2 = 2. Упорно получается значение «2».

Можно остановиться в любой момент, посчитать количество вершин, ребер и граней. Но вы должны понимать, что всегда можно привести к ситуации, в которой останется одна вершина. Поэтому у любой картинки на сфере эйлерова характеристика равна двум, ибо эту картинку можно свести к простейшему случаю «одна вер­шина, одна грань, ноль ребер».

Мы получаем противоречие. На торе всегда ноль, а на сфере – два. Но 2 не равно 0. Значит, это разные топологические фигу­ры, что, впрочем, каждый из вас и так знал. Но вопрос не в том, чтобы доказать очевидный факт, а в том, чтобы наработать язык, который поможет нам этот факт заметить в других пространствах. В частности, в пространстве большего числа измерений. А в боль­шем числе измерений верно в точности то же самое, только по­является то, что называется «трехмерные грани». И получается следующее выражение:

В^Р + Г^Т.

Здесь Т – количество трехмерных граней. Так выглядит эйлеро­ва характеристика для четырехмерного пространства, в котором лежит трёхмерный объект. В общем случае у формулы тот же вид В^Р + Г^Т +... и так далее, в n‑мерном пространстве, кото­рое довольно сложно представить. Если изучить, что происходит при стирании вершины, ребра, грани, трехмерной грани, будет об­наруживаться, что значение нашего выражения не изменится. Вот основываясь на примерно таких вещах, но гораздо более сложных, была установлена справедливость гипотезы Пуанкаре.

В 2002 году, когда доказали гипотезу Пуанкаре, газета «Изве­стия» напечатала о ней статью. Помнится, в СССР было 2 основ­ных газеты: «Правда» и «Известия». И все знали, раз написано в газете «Известия», значит факт. Но в 2002 году «Известия» от­ступили от этого замечательного правила, написав математиче­скую формулировку гипотезы Пуанкаре в таком виде, в котором она являла собой полную чушь. Они не удосужились позвонить ни одному грамотному математику и очень сильно опозорились (впрочем, мало перед кем).

А теперь – обещанное в первой лекции доказательство того, что в футбольном мяче ровно 12 пятиугольных лоскутков.

Рисуем на сфере картину футбольного мяча. Он должен состо­ять из шестиугольных и пятиугольных лоскутков. В любой верши­не должны сходиться ровно 3 ребра. В остальном он может быть совершенно произвольным.

Давайте обозначим за ж – число шестиугольников, за у – чи­сло пятиугольников.

Сколько тогда граней у нашего многогранника, нарисованного на сфере, то есть на футбольном мяче?

 

Слушатель: Граней?

А.С.: Да.

Слушатель: х + у.

А.С.: Правильно. Ровно столько, сколько в сумме количеств шести‑ и пятиугольников.

Г = х + у

(Г – количество граней).

Чему равно количество вершин и чему равно количество ребер? Посчитаем наивно. Сколько вершин у шестиугольника?

 

Слушатели: 6.

А.С.: 6. Всего х шестиугольников. Значит, у всех шестиуголь­ников вершин...

 

Слушатель: 6ж.

А.С.: А у пятиугольников?

 

Слушатель: Ъу.  

А.С.: Значит, пишем 6ж + 5у, но это не совсем то, что надо.

Обозначим поэтому не «В», а «М»,

М = 6ж + Ьу.

А.С.: Почему это не то, что надо?

Слушатели: Потому что вершины совпадают.

А.С.: Если мы разрежем мяч на лоскутки или, наоборот, не на­чнем сшивать, то сколько будет вершин у всех лежащих на столе лоскутков? Именно столько, 6ж + Ьу. А когда мы сошьем, некото­рые вершины совпадут. Что надо сделать с этим числом, чтобы получить правильное число вершин?

Слушатель: Разделить на 3.

А.С.: Да. Правильно, потому что ровно – не больше не меньше, а ровно – 3 разных грани сходятся в каждой вершине:

р ₌   ^м  ₌ 6ж + Ьу 3 3 '

Сколько ребер? Первый вопрос: сколько ребер до того, как мы сшивали? Столько же, сколько было до сшивания вершин:

М = 6ж + Ьу.

У любого многоугольника вершин и ребер одинаковое количество. А на что делить?

 

Слушатели: На 2:

_D _ 6х + Ьу = 2 '

Каждое ребро мы считали ровно два раза.

Теперь мы воспользуемся формулой Эйлера. Формула Эйлера утверждает, что В – Р + Г = 2. Подставим в нее выражения через «ж» и «у»:

 

6х + Ьу 6х + Ьу

д–^ 2 +Х + У = 2.

Цель этой формулы – доказать, что у = 12. Давайте решать.

6ж: 3 = 2ж, 6ж: 2 = Зж,

2ж – Зж + ж = 0.

Иксы ушли. Осталось уравнение относительно «у»:

 

f‑| + у = ²‑

Умножим все уравнение на 6, чтобы избавиться от знаменателя. Умножим и правую, и левую часть. Справа будет 12. Слева будет: 10у – 15 у + 6 у. Отсюда

у = 12.

Чудеса, да? И никакого мошенничества!

Слушатель: Что‑то тут есть от фокуса.

А.С.: Курс «Математика для гуманитариев» – это курс черной магии плюс ее разоблачение. В чем здесь фокус? Природа фоку­са в том, что сократились все шестиугольники. Получается, они ни на что не влияют. Можно любое количество шестиугольников вклеить дополнительно в любой футбольный мяч, так как все х сокращаются9. А с «у» вы не можете сделать ничего, потому что сколько бы пятиугольников ни было у нас в запасе, их количество должно удовлетворять уравнению. А математики еще 3 тысячи лет назад научились решать линейные уравнения. У этих уравнений в нормальной ситуации всегда одно решение: у = 12 – единствен­ное решение нашего уравнения. Поэтому сколько бы вас ни проси­ли сшить футбольный мяч из 11 пятиугольников – не получится. Слушатель: А если пятиугольников будет 24?

А.С.: Вы сошьете два футбольных мяча. Один не сошьется. Где‑то будут торчащие, несшиваемые части.

Давайте теперь посмотрим на обычную бесконечную во все сто­роны плоскость. С одной стороны, это более простой объект, чем сфера, но, с другой стороны, она бесконечна во все стороны. Бес­конечность – это такой краеугольный камень математики. И как с ней можно быть «на ты» – это очень важная тема. Кажется,

плоскость, она и есть плоскость, посмотрел вокруг – везде плос­кость. Но ведь она бесконечная... А как, кстати, можно понять, что земля не плоская?

В принципе, как я понимаю, то что древние люди считали Зе­млю плоской – это сказки. Люди всегда знали, что она не плос­кая. Когда по морю идет корабль, сначала на горизонте появля­ются паруса. Как еще, кроме как искривлением, можно это объяс­нить?

Слушатель: Может быть, Земля не ровная именно в этом ме­сте...

А.С.: От того, что ты видишь паруса, до понимания, что Земля может быть устроена как шар, уже, в общем, недалеко.

Люди, на самом деле, в прошлом совершали и более великие открытия. Знаете, когда в первый раз (по крайней мере, доку­ментально) была высказана идея о конечности скорости света? В 1676 году датский астроном Тихо Браге стал наблюдать затме­ния спутников Юпитера. И заметил странности в их периодично­сти: то затмения наступали позже прогнозируемого момента, то раньше. Тогда он предложил совершенно невероятное объяснение. Он предположил, что такое могло бы быть, если бы скорость света была конечна. Так как Земля и Юпитер то приближаются друг к другу, то отдаляются, мы видим объект, который ближе, рань­ше, чем тот, который находится дальше. За счет этого и возникает неполная периодичность в затмениях. Но тогда нужно было при­знать, что значение этой скорости настолько велико, что оно пре­восходит всякое наше воображение. И Браге оценил его как 225 ты­сяч километров в секунду. Он назвал величину, которая равна 75% от верного значения. Но тогда ученый мир был еще не готов к та­ким смелым идеям, и к этому предположению отнеслись с большим сомнением.

Или другая история.

У вас в сумке, наверное, живет зарядка от телефона или науш­ники. В каком они будут состоянии? Обычно получается страшный запутанный провод.

Вопрос: можно ли его как‑то распутать, если вы еще и кон­цы провода свяжете, чтобы он стал замкнутым, как окружность? Чтобы он стал после этого распутывания нормальной, идеальной окружностью?

 

Слушатель: Нельзя.

А.С.: Иногда можно, иногда нельзя. Это – задача из теории узлов. Какие‑то виды узлов можно распутать, какие‑то нельзя. Сейчас я расскажу историю, которая может оказаться неправдой. Я слышал ее на лекции примерно 13 лет назад. Знаменитая про­блема узлов, топологических типов узлов, встала в первый раз на корабле пирата Дрейка в конце XVI века. Один из матросов это­го корабля тоже занимался узлами. Он завязывал много разных морских узлов и заметил, что некоторые из них – по сути один и тот же узел. Надо просто в одном месте потянуть, в другом прис­пустить шнур, и из первого узла получится второй (имеется в виду, что при этом концы узла должны оставаться связанными). Такие узлы называются «эквивалентными». И пирату в голову пришла идея классифицировать все виды узлов. Какие друг в друга пере­водятся без разрезания, а какие нет. Ему это не удалось, в чем, якобы, он честно признался.

Прошло 400 лет. И только совсем недавно был сделан большой прорыв в решении задачи об узлах. Сделали его отечественные ма­тематики Максим Концевич, Виктор Васильев и Михаил Гусаров.

Идея решения в том, что берут два узла, пишут для них неко­торые математические выражения, и если они разные, то и узлы тоже разные.

Вернемся к плоскости. «Простой» вопрос: какими много­угольниками можно замостить плоскость?

Что значит «замостить многоугольниками»? Я имею в виду сле­дующее. Вы заходите в магазин и выбираете себе паркет. Понра­вившийся вам паркет состоит из одинаковых дощечек такой формы (рис. 42):

Кто‑то в страшном сне придумал такую форму. И таких до­щечек у вас немыслимое количество. Вопрос: «Можно ли собрать

 

из них паркет? Или они при сборке входят в противоречие сами с собой?»

Слушатель: Ну. скорее всего, центр еще получится, а вот по краям комнаты будут проблемы.

А.С.: Вы. наверное, уже видите, что не всякими плитками мож­но замостить плоскость.

Но доказать, что какой‑то конкретной плиткой нельзя замо­стить довольно сложная задача. На самом деле, до сих пор не классифицированы даже все виды пятиугольников, которыми можно замостить плоскость. Найдено несколько пятиугольников, которыми можно замостить плоскость, но неизвестно, есть ли дру­гие. Открытая проблема10. Но тем не менее методами Леонарда Эйлера можно доказать следующую теорему.

Теорема. Не существует ни одного выпуклого 7‑угольника, ко­торым можно замостить плоскость. Более того, восьми‑, девяти‑, десяти‑ и т. д. угольника тоже не существует.

А что такое «выпуклый»? Выпуклая фигура это такая фи­гура, у которой, если вы выбрали любые две ее точки, то весь отрезок между ними лежит внутри этой фигуры, не выходит за ее пределы.

 

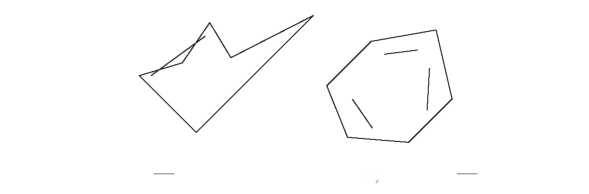
Рис. J _t 3. Слова нсвыпуклая фигура, справа выпуклая.

Выпуклость одно из фундаментальных понятий математики. Такое простое определение, а на нём построена огромная сложней­шая теория с зубодробительными теоремами.

 

Почему же теорема требует выпуклости? Представьте себе цар­скую корону (рис. 44). Паркетина такой формы хотя и является 7‑угольником, но он не выпуклый. Ниже мы увидим, что такими паркетинами МОЖНО замостить плоскость. Значит, если не тре­бовать выпуклости, доказать указанную выше теорему нельзя она просто неверна. Нельзя огульно утверждать, что паркетов из 7‑ уголышков не бывает. Не бывает только из выпуклых.

Рис. 44‑ Д° царской короны страшно даже пальцем дотронуться!

Сколько углов? Семь. Однако такой плиткой можно без проблем замостить плоскость.

Переворачиваем фигурку и вставляем корону в корону, а потом еще раз. два... (см. рис. 45).

Слушатель: А в конце как?

А.С.: До бесконечности. Мы же говорим о бесконечной плос­кости. Полосу сделать у нас получилось... (бесконечную в обе стороны). Ну. а если можно полосу, то мы ее размножаем неогра‑

 

ниченно вниз и вверх, и всё. Мы «запаркетили» всю плоскость. А теперь я нарисую выпуклый семиугольник (рис. 46).