

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Приходовский М.А.
Алгебра
(электронное учебное пособие по практике)
ИПМКН ТГУ, группы 932024, 932025
Весна - 2021
ПРАКТИКА 1. 11.2.2021.
Продолжение и повторение за конец 1 семестра.
П. 1. Матрица Грама и её свойства.
Пусть 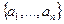 - система векторов. Матрица, состоящая из всех скалярных произведений:
- система векторов. Матрица, состоящая из всех скалярных произведений:
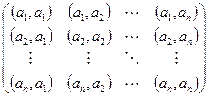
Называется матрицей Грама данной системы векторов. Во-первых, очевидно, что она симметрична.
Свойства.
0. Если система векторов ортогональная, то матрица Грама диагональная.
1. Система векторов является линейно-зависимой тогда и только тогда, когда матрица Грама вырождена.
Пусть система ЛЗС. Тогда какой-либо вектор линейно выражается через остальные. Для определённости обозначений, допустим, что это n-й вектор:  , тогда последняя строка матрицы представляется в виде линейной комбинации остальных строк, и определитель равен 0:
, тогда последняя строка матрицы представляется в виде линейной комбинации остальных строк, и определитель равен 0:
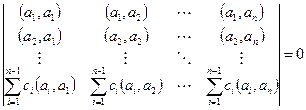
Обратно. Допустим, что определитель Грама равен 0. Тогда есть линейная зависимость между строками, то есть некоторая линейная комбинация всех строк равна нулевой строке.
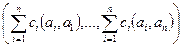 =
= 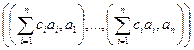 =
= 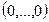 .
.
Тогда вектор 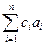 ортогонален всем векторам из
ортогонален всем векторам из 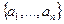 . Но он является их линейной комбинацией и принадлежит подпространству, ими порождённому. Поэтому единственная возможность – что сам этот вектор есть 0, то есть
. Но он является их линейной комбинацией и принадлежит подпространству, ими порождённому. Поэтому единственная возможность – что сам этот вектор есть 0, то есть 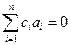 , но при этом коэффициенты
, но при этом коэффициенты 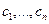 не все нулевые, ведь они отражают линейную зависимость строк матрицы Грама. Это означает, что система
не все нулевые, ведь они отражают линейную зависимость строк матрицы Грама. Это означает, что система 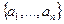 ЛЗС.
ЛЗС.
2. Определитель матрицы Грама неотрицателен.
Если система ЛЗС, то, как выше доказано, он равен 0, значит неотрицателен. Теперь осталось рассмотреть ЛНС 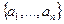 .
.
Пусть для начала, это n векторов n-мерного пространства. Тогда матрицу Грама можно представить в виде произведения двух матриц, где в первой векторы 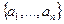 расположены по строкам, а во второй по столбцам. Произведения всех строк на столбцы как раз и образуют все скалярные произведения, присутствующие в матрице Грама.
расположены по строкам, а во второй по столбцам. Произведения всех строк на столбцы как раз и образуют все скалярные произведения, присутствующие в матрице Грама.
|
|
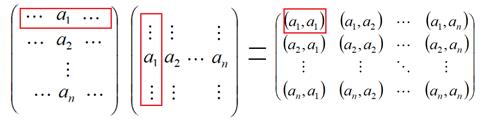
В таком случае, определитель Грамма равен 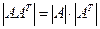 =
= 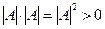 . Итак, он равен 0, если система ЛЗС, и больше нуля, если ЛНС.
. Итак, он равен 0, если система ЛЗС, и больше нуля, если ЛНС.
Теперь рассмотрим систему из k векторов в n-мерном пространстве. В этом случае мы не можем напрямую записать матрицу Грама как произведение двух квадратных матриц, а только как прямоугольных.
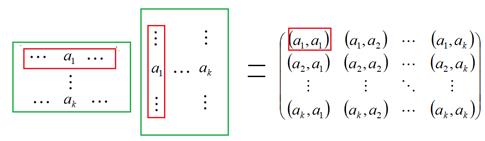
Так как система ЛНС, то линейная оболочка – k-мерное подпространство. В этом случае мы можем достроить до базиса из n векторов, рассмотрев ортонормированную систему из 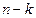 векторов, ортогональных всем
векторов, ортогональных всем 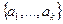 . Тогда прямоугольные матрицы будут достроены до квадратных, причём их произведение будет матрицей Грама порядка n с таким строением:
. Тогда прямоугольные матрицы будут достроены до квадратных, причём их произведение будет матрицей Грама порядка n с таким строением:

Её определитель больше 0, согласно доказанному выше. Но он равен произведению минора
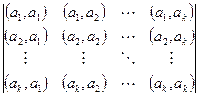 на минор Е порядка
на минор Е порядка 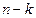 , который в свою очередь равен 1. Поэтому указанный минор тоже больше 0.
, который в свою очередь равен 1. Поэтому указанный минор тоже больше 0.
*
Можно обобщать понятие определителя на прямоугольные матрицы, рассматривая величину 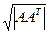 . При этом необходимо учитывать, что слева должна стоять именно та матрица, у которой число строк меньше числа столбцов. Если наоборот, то произведение
. При этом необходимо учитывать, что слева должна стоять именно та матрица, у которой число строк меньше числа столбцов. Если наоборот, то произведение 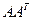 будет вырожденной матрицей, так как соответствует системе из n векторов в k-мерном пространстве, при
будет вырожденной матрицей, так как соответствует системе из n векторов в k-мерном пространстве, при 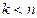 такая система ЛЗС.
такая система ЛЗС.
1 2 1 1 3 5 3 5
1 1 2 1 1 3 2 4
3 1 5 4 10
100 + 60 +60 -50 -80 -90 = 220 – 220 = 0
Пример. Дана система векторов 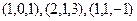 . Найти определитель матрицы, построенной из них. Найти матрицу Грама и её определитель, сравнить результаты.
. Найти определитель матрицы, построенной из них. Найти матрицу Грама и её определитель, сравнить результаты.
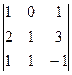 =
= 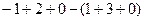 =
= 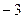 .
.
Все скалярные произведения найдём с помощью умножения 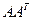 :
:
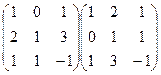 =
=  - матрица Грама.
- матрица Грама.
Её определитель равен 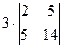 =
= 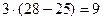 =
= 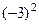 .
.
Решение.

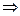
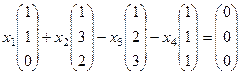
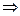 однородная система уравнений
однородная система уравнений 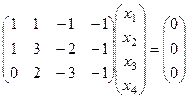 .
.
Преобразуем основную матрицу методом Гаусса.





базисный минор в первых трёх столбцах, свободная переменная 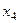 .
.
Из последнего  , из 2-го
, из 2-го 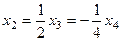 . Тогда из 1-го
. Тогда из 1-го
|
|
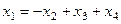 =
= 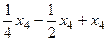 =
= 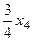 .
.
Общее решение: 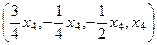 . ФСР:
. ФСР: 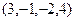 .
.
Пересечение одномерно. Если посчитаем линейную комбинацию векторов 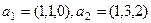 с коэффициентами
с коэффициентами 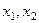 , либо
, либо
 с коэффициентами
с коэффициентами  , получим одно и то же:
, получим одно и то же:
Подставить в 
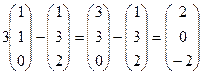 ,
, 
Можно сократить на 2 и в качестве базиса можно принять вектор  . Ответ. базис пересечения:
. Ответ. базис пересечения:  .
.
Пересечение может оказаться и 2-мерным, то есть 2 указанные плоскости совпадать. Посмотрим, как это влияет на решение, увидим из следующего примера.
Задача 2. В трёхмерном пространстве заданы два 2-мерных
подпространства, с помощью систем векторов:
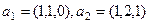 ,
, 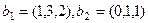 . Найти базис их пересечения.
. Найти базис их пересечения.
Решение. Строим систему уравнений, как и в прошлой задаче.
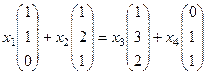
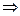
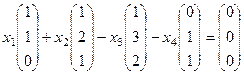
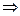 однородная система уравнений
однородная система уравнений 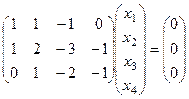 .
.
Преобразуем основную матрицу методом Гаусса.


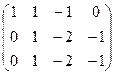

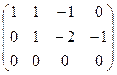
Третье уравнение состоит из нулей, ранг системы равен 2.
Из второго,  , тогда из 1-го
, тогда из 1-го
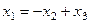 =
=  =
=  .
.
Общее решение  ,
,
ФСР  .
.
Подставим в 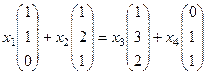
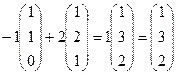 ,
, 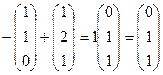 .
.
Таким образом, 2 вектора второй системы получились базисом пересечения. Плоскости совпадают.
Задача 3. Найти базис пересечения двух трёхмерных подпространств 4-мерного пространства.
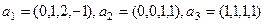 ,
,
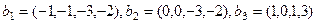 .
.
Решение.
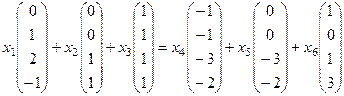 ,
,
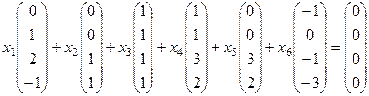 ,
,
Строим и преобразуем основную матрицу.
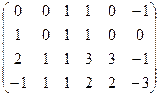

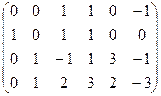





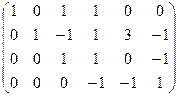
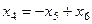 ,
,
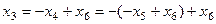 =
=  .
.
 =
= 

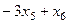 =
= 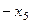 .
.
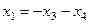 =
= 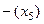
 =
= 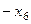 .
.
Общее решение: 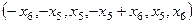 .
.
ФСР: 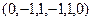 ,
,  .
.
Подставляем в
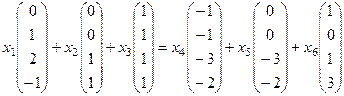
1)  ,
,
2)  .
.
Ответ. Базис пересечения: 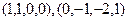 .
.
ПРАКТИКА 2. 13.2.2021.
Нахождение определителей Грама для систем функций.
 , где
, где 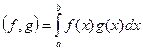
Каждое х как координата, континуум координат.
Матрица Грама невырождена  система функций ЛНС.
система функций ЛНС.
Задача 1 (а,б).
а) Даны две функции на (0,1): 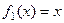 ,
, 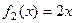 . (ЛЗС)
. (ЛЗС)
б) Даны две функции на  :
:
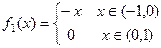 ,
, 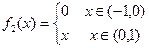 . (ЛНС)
. (ЛНС)

Найти определители Грама этих систем.
а) 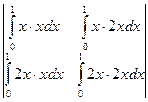 =
=  =
= 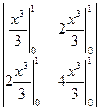 =
=
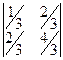 =
=  .
.
б) 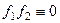 , значит, и интеграл от
, значит, и интеграл от 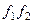 равен 0.
равен 0.
 =
=  =
= 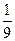 .
.
Задача 2 (комбинированная, на поиск пересечения и проекции).
Даны два подпространства, с помощью линейных оболочек систем векторов:
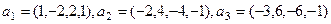 ,
,
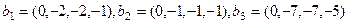 .
.
Найти базис их пересечения, и проекцию вектора 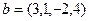 на пересечение.
на пересечение.
Решение. Составляем выражение:

Переносим в левую часть:

Решаем однородную систему с такой основной матрицей:
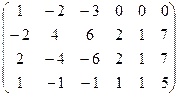

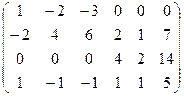





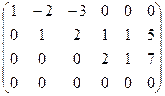
Ранг 3. Базисный минор можно составить из 1,2,5 столбцов, чтобы коэффициенты по возможности были 1.

Система:

Из третьего 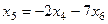 ,
,
Тогда из второго 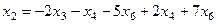

Из первого 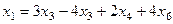 ,
, 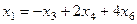
Общее решение
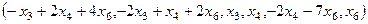 .
.
ФСР  ,
, 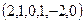 ,
, 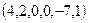 .
.
Каждое подставить в



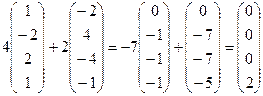 .
.
Итак, получили векторы (0,0,0,0), (0,0,0,1), (0,0,0,2).
|
|
То есть, пересечение одномерно, базис (0,0,0,1).
Проекция вектора 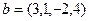 на а = (0,0,0,1), это последняя координата, то есть 4.
на а = (0,0,0,1), это последняя координата, то есть 4.
Либо по формуле  то же самое.
то же самое.
Элементы теории множеств.
Задача 1. Дано: 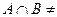 Ø,
Ø, 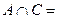 Ø. Возможно ли, что
Ø. Возможно ли, что 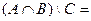 Ø?
Ø?
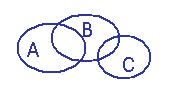
Нет, 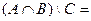
 но
но 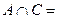 Ø, тогда
Ø, тогда 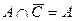 .
.
 =
= 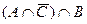 =
= 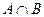 , а про это множество в условии сказано, что оно непусто.
, а про это множество в условии сказано, что оно непусто.
Задача 2. Доказать, что
1) 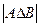 =
= 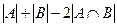
2) 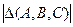 =
= 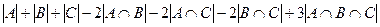
(множество элементов, принадлежащих лишь одному из множеств).
2а)  =
= 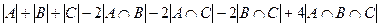
n=2 очевидно: 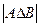 =
= 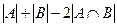 при объединении, все элементы пересечения учтены 2 раза, их и нужно вычесть.
при объединении, все элементы пересечения учтены 2 раза, их и нужно вычесть.
n=3: два разных подхода к образованию симметрической разности.
А) Если определять 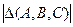 как множество элементов, принадлежащих только одному из множеств:
как множество элементов, принадлежащих только одному из множеств:
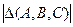 =
= 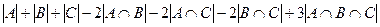

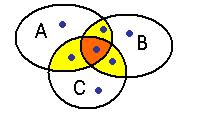
центральную часть прибавили 3 раза, вычли 6 раз, значит, нужно прибавить 3 раза, чтобы характеристическая функция приняла значение 0.
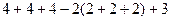 = 3, в симметрической разности тоже 3 точки.
= 3, в симметрической разности тоже 3 точки.
Б) Если последовательно, то
 =
= 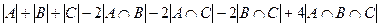
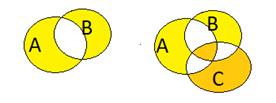
В этом случае центральная часть присутствует, и её характеристическую функцию нужно прибавить 4 раза.
Задача 3. Доказать, что  .
.
Идея решения: Множество всех подмножеств из k элементов, при всех k, как раз и составляет множество всех подмножеств.
Задача 4. Дано универсальное множество 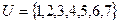 и множества
и множества 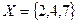 ,
,  ,
, 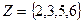 .
.
1) Найти множество  .
.
2) Записать булеан множества 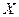 .
.
Решение.
1) 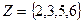
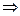
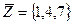 .
.
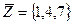

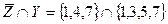 =
= 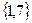 .
.
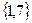
 =
=  .
.
2) Множество всех подмножеств 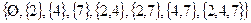 .
.
Задача 5. Из 100 студентов факультета, в олимпиаде по математике участвовали 28, по физике 42, по информатике 30. Одновременно в двух олимпиадах участвовали: по математике и физике 10 студентов, по математике и информатике 8 студентов, по физике и информатике 5 человек. При этом во всех трёх олимпиадах приняли участие 3 человека. Сколько студентов не участвовали ни в одной олимпиаде?
Решение. По формуле включений и исключений,
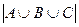 =
= 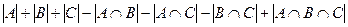 .
.
Найдём число студентов, которые участвовали хотя бы в одной олимпиаде. 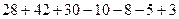 =
= 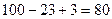 .
.
Таким образом, 20 студентов не участвовали ни в одной олимпиаде.
Практика 3
Задача 6 (РП). На кафедре 13 человек знают иностранные языки. Причём каждый из них владеет хотя бы одним иностранным языком. 10 человек знают английский, 7 человек немецкий, 6 французский. При этом 5 человек знают английский и немецкий, 4 знают английский и французский, 3 знают немецкий и французский.
|
|
1) Сколько человек знают 3 языка?
2) Сколько человек знают только 2 языка?
3) Сколько человек знают только английский?
Решение.
По формуле включений и исключений,
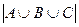 =
= 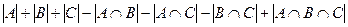 .
.
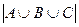 = 13.
= 13. 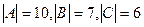 .
.
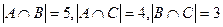 .
.
Тогда число людей, знающих все 3 языка,  .
.
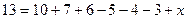
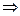
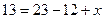
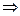
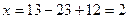 .
.
Англ+нем: всего 5 чел, из них 2 знают и третий язык, т.е. только англ+нем 3.
англ + фр 4, только англ + фр 2
нем + фр 3, только нем + фр 1.
Далее, англ 10, вычесть 3,2,2. Остаётся 3 - только англ.
Аналогично, нем 7, вычесть 3,1,2, осталось 1.
фр 6, вычесть 2,1,2, осталось 1.

1) Сколько человек знают 3 языка? 2
2) Сколько человек знают только 2 языка? 6
3) Сколько человек знают только английский? 3
Задача 7.
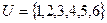 ,
, 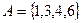 ,
, 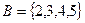 ,
,  .
.
Найти  . В ответе указать сумму и произведение всех чисел этого множества, а также мощность множества.
. В ответе указать сумму и произведение всех чисел этого множества, а также мощность множества.
Решение.
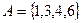 ,
, 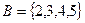
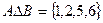 . Учитываем элементы, которые есть только в одном или другом множестве. 3 и 4 есть в обоих множествах, поэтому в симметрическую разность они не входят.
. Учитываем элементы, которые есть только в одном или другом множестве. 3 и 4 есть в обоих множествах, поэтому в симметрическую разность они не входят.
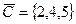 .
.
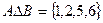 ,
, 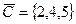 . Пересечение
. Пересечение  .
.
Ответ.  , сумма чисел равна 7, произведение 10, мощность 2.
, сумма чисел равна 7, произведение 10, мощность 2.
Задача 8.
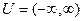 ,
, 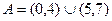 ,
, 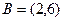 ,
, 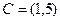 .
.
Найти  .
.
Решение.
1) 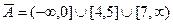 .
.
2) 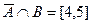
3)  =
= 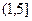 .
.
Задача 9.
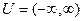 ,
, 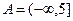 ,
, 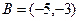 ,
,  .
.
Найти 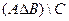 .
.
Решение.
Так как 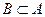 то
то  =
= 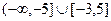 .
.
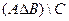 =
=  .
.
Ответ. 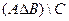 =
=  .
.
Задача 9-А
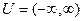 ,
, 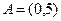 ,
,  ,
, 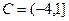 .
.
Найти  .
.
Решение. 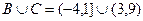 .
.

 =
= 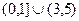 .
.
Перерыв
Задача 10. (Принцип индукции). Доказать, что 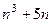 делится на 6 для любого
делится на 6 для любого 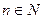 .
.
База индукции.  .
. 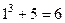 .
.
Индукционный шаг. Пусть верно для n, рассмотрим n+1.
 =
= 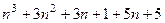 =
= 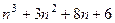 .
.
Выделим старое выражение отдельным слагаемым, а также константу, которая точно делится на 6.
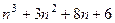 =
= 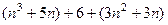 . Осталось доказать, что последнее слагаемое делится на 6. Оно точно делится на 3, поэтому осталось доказать, что
. Осталось доказать, что последнее слагаемое делится на 6. Оно точно делится на 3, поэтому осталось доказать, что 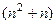 делится на 2.
делится на 2.
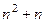 =
= 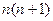 произведение соседних целых чисел, поэтому одно из них точно чётное, значит,
произведение соседних целых чисел, поэтому одно из них точно чётное, значит,  ,
,  .
.
Задача 11. (Принцип индукции). Доказать, что при любом натуральном 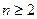 верно
верно 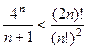 .
.
Решение.
Проверим при 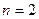 (база индукции).
(база индукции).
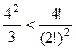

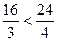

 . (При n=3: 16 < 20).
. (При n=3: 16 < 20).
Если верно при n, докажем, что и при  .
.
Составим выражение при  и докажем, что левая часть умножается на меньший коэффициент, чем правая.
и докажем, что левая часть умножается на меньший коэффициент, чем правая.
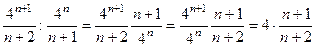 =
= 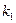 (для левой).
(для левой).
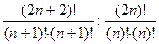 =
=  =
=  =
= 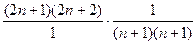 =
=
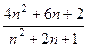 =
=  =
= 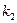 =
= 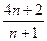 (для правой).
(для правой).
Соотношение.
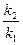 =
= 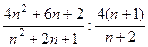 =
= 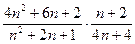 =
=
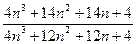 . В выражении
. В выражении 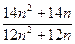 числитель больше знаменателя. Тогда
числитель больше знаменателя. Тогда 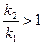 . Неравенство сохранится при переходе от n к n+1.
. Неравенство сохранится при переходе от n к n+1.
Если сократить ранее, то 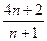
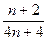 =
= 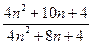 =
= 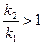 .
.
Задача 12. Доказать, что множества  и
и 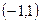 равномощны. Построить биективное отображение.
равномощны. Построить биективное отображение.
Решение. 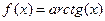 биективно отображает
биективно отображает  на
на
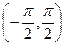 . Тогда
. Тогда 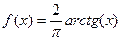 биекция
биекция  на
на 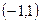 .
.
Задача 12-А. Доказать, что множества  и
и 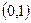 равномощны. Построить биективное отображение.
равномощны. Построить биективное отображение.
|
|
Как и в прошлой задаче, но 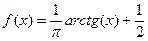 (прошлую функцию сжать в 2 раза и поднять на 0,5).
(прошлую функцию сжать в 2 раза и поднять на 0,5).
Задача 13 (РП). Доказать, что любые два интервала 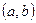 и
и  на прямой равномощны.
на прямой равномощны.
Решение. 2 способа:
1) Построить биекцию.
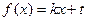 ,
, 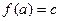 ,
, 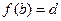 .
.
Получится система уравнений 
Вычесть 1-е из 2-го 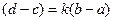 ,
, 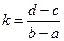 ,
,
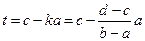 . Биективное отображение существует.
. Биективное отображение существует.
2) По теореме Кантора-Бернштейна.
Построить 2 инъективных отображения, 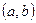 в
в  и
и  в
в 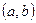 .
.
 ,
, 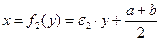 . (малые коэфф, кратно меньше отношения длин интервалов). Каждое множество равномощно подмножеству второго, эти множества равномощны.
. (малые коэфф, кратно меньше отношения длин интервалов). Каждое множество равномощно подмножеству второго, эти множества равномощны.
ПРАКТИКА 4. 20.2.2021.
Задача 13. Доказать, что множества 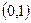 и
и 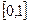 равномощны.
равномощны.
Решение. 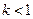 ,
,
 ,
, 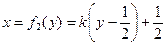 .
.
Каждое множество отображается на часть второго с помощью инъективной функции.
По теореме Кантора-Бернштейна, они равномощны, континуум.
Задача 14. Доказать, что множества 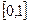 и
и 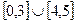 равномощны.
равномощны.
Решение.
Два инъективных отображения:  .
.
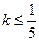
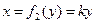 .
.
По теореме Кантора-Бернштейна, они равномощны.
Задача 15. Найти мощность множества корней уравнения  .
.
Решение. 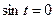
 ,
, 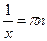 ,
, 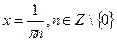 .
.
Существует биективное отображение между множеством корней этого уравнения и 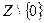 , а это счётное множество.
, а это счётное множество.
Графики функций 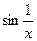 и
и  выглядят так:
выглядят так:
 и
и 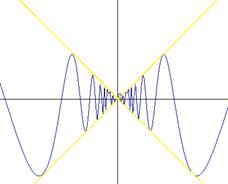
Задача 16. Доказать, что если 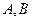 - множества корней многочленов
- множества корней многочленов 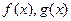 соответственно, то
соответственно, то  - множество корней произведения многочленов
- множество корней произведения многочленов  .
.
Решение.  = 0 тогда и только тогда, когда один или второй множитель равен 0,
= 0 тогда и только тогда, когда один или второй множитель равен 0, 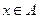 или
или 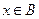 , то есть
, то есть 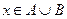 .
.
Задача 17. На множестве  задано бинарное отношение:
задано бинарное отношение:  . Представить с помощью графа и матрицы, выяснить свойства (рефлексивность, симметричность, транзитивность), является ли отношением эквивалентности или отношением порядка?
. Представить с помощью графа и матрицы, выяснить свойства (рефлексивность, симметричность, транзитивность), является ли отношением эквивалентности или отношением порядка?
Решение.
Рефлексивность очевидна: для пары 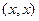 получается
получается 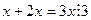 .
.
Симметричность: 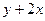 =
=  =
=
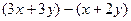 , и здесь каждое делится на 3.
, и здесь каждое делится на 3.
Транзитивность: пусть  и
и 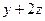 делятся на 3, проверим это свойство для
делятся на 3, проверим это свойство для  .
.
 =
=  =
=  , здесь каждое делится на 3. Значит, отношение транзитивно.
, здесь каждое делится на 3. Значит, отношение транзитивно.
Итак, это отношение эквивалентности (рефлексивно, симметрично, транзитивно).
Запишем сами эти числа вида 
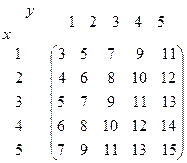
Укажем «1», где делится на 3:

Граф отношения:
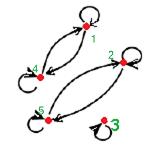
Из строения матрицы видно, что отношение рефлексивно и симметрично. Отношение эквивалентности.
Классы эквивалентности  видны на графе (множество распадается на 3 непересекающихся подмножества).
видны на графе (множество распадается на 3 непересекающихся подмножества).
Подматрицы из 1,4 строки и 1,4 столбца,
2,5 строка и 2,5 столбец, 3 строка 3 столбец.
В 1,4 строках не содержится «1» нигде кроме этих же номеров столбцов.
- Перерыв -
Задача 18. Фундированные множества (задача с монетами).
Каждую минуту автомат меняет монету, выдавая любое количество любых монет, но меньшего достоинства (видов монет конечное число). Доказать, что рано или поздно у игрока не останется ни одной монеты.
Решение. Пусть есть k видов монет. Множество монет, имеющееся в определённый момент, можно описать набором чисел 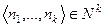 .
.
Отношение порядка введём следующим образом.
Если 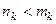 то
то  ,
,
Если  то сравнение по
то сравнение по  номеру и так далее.
номеру и так далее.
Набор 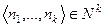 при каждом действии уменьшается (в смысле введённого порядка). При этом множество
при каждом действии уменьшается (в смысле введённого порядка). При этом множество 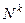 фундировано (доказано в лекциях). Таким образом, процесс должен оборваться.
фундировано (доказано в лекциях). Таким образом, процесс должен оборваться.
.
Задача 19. (РП). Пусть X и Y - два непересекающихся частично упорядоченных множества. На их объединении задан частичный порядок: внутри каждого множества элементы сравниваются как и прежде, а любой элемент 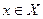 по определению меньше любого элемента
по определению меньше любого элемента 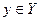 . Будет ли такой порядок линейным? Почему?
. Будет ли такой порядок линейным? Почему?
Частичный порядок, следовательно, 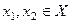 или
или 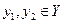 несравнимые в исходном множестве, и после объединения будут несравнимы.
несравнимые в исходном множестве, и после объединения будут несравнимы.
Задача 20. Доказать, что  можно вполне упорядочить.
можно вполне упорядочить.
Решение.  (это не декартово произведение)
(это не декартово произведение)  , порядок:
, порядок: 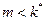 .
.
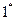 предельный элемент (не существует непосредственного предшествующего).
предельный элемент (не существует непосредственного предшествующего).
Линейный порядок был на каждом из множеств, линейный порядок на объединении. Кроме того, множество фундированное.
(1 есть наименьший элемент). Линейно упорядоченное и фундированное, значит, вполне упорядоченное.
Задача 21. Доказать методом математической индукции, что
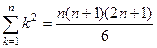 .
.
Решение. База индукции. Можно непосредственно проверить на малых числах, например 1 или, если интересно, 2 (достаточно 1).
 .
. 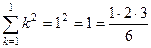 .
.
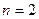 .
. 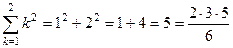 .
.
Индукционный шаг. Рассмотрим, следует ли из выполнения этого равенства для номера 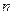 его выполнение для номера
его выполнение для номера  .
.
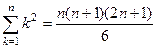 ,
, 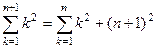 =
=
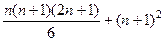 .
.
С другой стороны, для  выражение бы выглядело так:
выражение бы выглядело так: 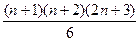 .
.
Мы должны убедиться, что:
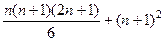 =
= 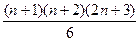 .
.
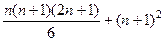 =
= 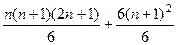 , таким образом, остаётся сравнить
, таким образом, остаётся сравнить 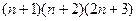 и
и  .
.
Сократим на 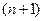
сравнить 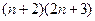 и
и 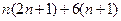 .
.
Справа и слева 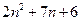 .
.
Задач

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!