Наиболее типичная операция, выполняемая над бинарными деревьями – обход дерева. Обход – это процедура, при выполнении которой каждый узел обрабатывается ровно один раз некоторым единым образом. Обход дерева заключается в разбиении дерева на корень, левое и правое поддеревья и применении к каждому из поддеревьев соответствующей процедуры обработки до тех пор, пока в процессе разбиения не будет получено пустое дерево.
Полный обход дерева дает линейную расстановку узлов, что облегчает выполнение многих алгоритмов. Существует три принципа упорядочения, которые естественно вытекают из структуры дерева. Как и саму древовидную структуру, их удобно выразить с помощью рекурсии. Им соответсвуют три левосторонних алгоритма обхода.
Нисходящий (прямой) обход выполняется по формуле “корень-левый-правый” (К-Л-П).
1. обработать корневой узел;
2. обойти левое поддерево в нисходящем порядке;
3. обойти правое поддерево в нисходящем порядке.
Трасса нисходящего обхода дерева рис. 68: A B C D E F.
Восходящий (концевой) обход выполняется по формуле “ левый-правый-корень” (Л-П-К).
1. обойти левое поддерево в восходящем порядке;
2. обойти правое поддерево в восходящем порядке;
3. обработать корневой узел.
Трасса восходящего обхода дерева рис. 68 C D B F E A.
Смешанный (обратный) обход выполняется по формуле “ левый—корень-правый” (Л-К-П).
1. обойти левое поддерево в смешанном порядке;
2. обработать корневой узел;
3. обойти правое поддерево в смешанном порядке.
Трасса смешанного обхода дерева рис. 68: С B D A E F.
Заметим, что при различных алгоритмах обхода порядок обработки терминальных узлов не изменяется (содержимое терминальных узлов в трассах обхода выделено жирным шрифтом).
Ниже приведена процедура, распечатывающая трассу нисходящего обхода бинарного дерева – последовательность информационных полей узлов дерева.
| Procedure KLP(root: PTree);
| { root – указатель на корень дерева }
|
| begin
|
|
| if root <> nil then begin
| { дерево не пусто? }
|
| writeln(root^.info);
| { распечатать информ. поле корневого узла }
|
| KLP(root^.left);
| { обойти левое поддерево в нисходящем порядке }
|
| (* 1 *) KLP(root^.right)
| { обойти правое поддерево в нисходящем порядке }
|
| (* 2 *) end;
|
|
| (* 3 *) end;
|
|
| | | | | | |
Таблица 4. Трасса состояний стека при работе процедуры нисходящего обхода бинарного дерева
Номер входа в процедуру
Номер уровня рекур- сии
|
Значение фактичес-кого параметра
|
Стек
|
Выход-ная трасса
|
Выход из уровня
| | Исходное состояние
| Конечное состояние
|
| 1
| 1
| ^A
| (-,-)
| (^A, *1*)
| A
|
|
| 2
| 2
| ^B
|
(^A, *1*)
| (^B, *1*)
(^A, *1*)
| B
|
|
| 3
| 3
| ^C
|
(^B, *1*)
(^A, *1*)
| (^C, *1*)
(^B, *1*)
(^A, *1*)
| C
|
|
| 4
| 4
| NIL
|
(^C, *1*)
(^B, *1*)
(^A, *1*)
| (NIL,*1*)
(^C, *1*)
(^B, *1*)
(^A,*1*)
|
|
|
| 4
| NIL
| (NIL,*1*)
(^C, *1*)
(^B, *1*)
(^A,*1*)
|
(^C, *1*)
(^B, *1*)
(^A, *1*)
|
| (*3*)
|
| 3
| ^C
| (^C, *1*)
(^B, *1*)
(^A, *1*)
| (^C, *2*)
(^B, *1*)
(^A, *1*)
|
|
|
| 5
| 4
| NIL
|
(^C, *2*)
(^B, *1*)
(^A, *1*)
| (NIL,*2*)
(^C, *2*)
(^B, *1*)
(^A, *1*)
|
|
|
| 4
| NIL
| (NIL,*2*)
(^C, *2*)
(^B, *1*)
(^A, *1*)
|
(^C, *2*)
(^B, *1*)
(^A, *1*)
|
| (*3*)
|
| 3
| ^C
| (^C, *2*)
(^B, *1*)
(^A,*1*)
|
(^B, *1*)
(^A, *1*)
|
| (*3*)
|
| 2
| ^B
| (^B, *1*)
(^A,*1*)
| (^B, *2*)
(^A, *1*)
|
|
|
| 6
| 3
| ^D
|
(^B,*2*)
(^A,*1*)
| (^D, *1*)
(^B, *2*)
(^A, *1*)
| D
|
|
| 7
| 4
| NIL
|
(^D, *1*)
(^B, *2*)
(^A, *1*)
| (NIL,*1*)
(^D, *1*)
(^B, *2*)
(^A, *1*)
|
|
|
| 4
| NIL
| (NIL,*1*)
(^D, *1*)
(^B, *2*)
(^A, *1*)
|
(^D, *1*)
(^B, *2*)
(^A, *1*)
|
| (*3*)
|
| 3
| ^D
| (^D, *1*)
(^B, *2*)
(^A, *1*)
| (^D, *2*)
(^B, *2*)
(^A, *1*)
|
|
|
| 8
| 4
| NIL
|
(^D, *2*)
(^B, *2*)
(^A, *1*)
| (NIL,*2*)
(^D, *2*)
(^B, *2*)
(^A, *1*)
|
|
|
| 4
| NIL
| (NIL,*2*)
(^D, *2*)
(^B, *2*)
(^A, *1*)
|
(^D, *2*)
(^B, *2*)
(^A, *1*)
|
| (*3*)
|
| 3
| ^D
| (^D, *2*)
(^B, *2*)
(^A, *1*)
|
(^B, *2*)
(^A, *1*)
|
| (*3*)
|
| 2
| ^B
| (^B, *2*)
(^A, *1*)
|
(^A, *1*)
|
| (*3*)
|
| 1
| ^A
| (^A, *1*)
| (^A, *2*)
|
|
|
| 9
| 2
| ^E
|
(^A, *2*)
| (^E, *1*)
(^A, *2*)
| E
|
|
| 10
| 3
| NIL
|
(^E, *1*)
(^A, *2*)
| (NIL,*1*)
(^E, *1*)
(^A, *2*)
|
|
|
| 3
| NIL
| (NIL,*1*)
(^E, *1*)
(^A, *2*)
|
(^E, *1*)
(^A, *2*)
|
| (*3*)
|
| 2
| ^E
| (^E, *1*)
(^A, *2*)
| (^E, *2*)
(^A, *2*)
|
|
|
|
|
|
|
|
|
|
|
| Номер входа в процедуру
| Номер уровня рекур- сии
| Значение фактичес-кого параметра
| Исходное состояние
стека
| Конечное состояние
стека
| Выход-ная трасса
| Выход из уровня
|
| 11
| 3
| ^F
|
(^E, *2*)
(^A, *2*)
| (^F, *1*)
(^E, *2*)
(^A, *2*)
| F
|
|
| 12
| 4
| NIL
|
(^F, *1*)
(^E, *2*)
(^A, *2*)
| (NIL, *1*)
(^F, *1*)
(^E, *2*)
(^A, *2*)
|
|
|
| 4
| NIL
| (NIL, *1*)
(^F, *1*)
(^E, *2*)
(^A, *2*)
|
(^F, *1*)
(^E, *2*)
(^A, *2*)
|
| (*3*)
|
| 3
| ^F
|
(^E, *2*)
(^A, *2*)
| (^F, *2*)
(^E, *2*)
(^A, *1*)
|
|
|
| 13
| 4
| NIL
|
(^F, *2*)
(^E, *2*)
(^A, *2*)
| (NIL, *2*)
(^F, *2*)
(^E, *2*)
(^A, *2*)
|
|
|
| 4
| NIL
| (NIL, *2*)
(^F, *2*)
(^E, *2*)
(^A, *2*)
|
(^F, *2*)
(^E, *2*)
(^A, *2*)
|
| (*3*)
|
| 3
| ^F
| (^F, *2*)
(^E, *2*)
(^A, *2*)
|
(^E, *2*)
(^A, *2*)
|
| (*3*)
|
| 2
| ^E
| (^E, *2*)
(^A, *2*)
|
(^A, *2*)
|
| (*3*)
|
| 1
| ^A
| (^A, *2*)
| (-, -)
|
| (*3*)
|
Для иллюстрации работы этой процедуры и построения трассы состояний стека будем использовать следующие обозначения:
^A – адрес узла дерева, в информационном поле которого хранится символ “A”;
(* 1 *) и (* 2 *) – адреса возврата из уровня рекурсивной процедуры, номер которой на 1 больше текущего;
(* 3 *) – адрес возврата из рекурсивной процедуры текущего уровня.
Трасса нисходящего обхода дерева, приведенного на рис. 68, содержится в таблице 4.
Виды бинарных деревьев
Сбалансированные деревья
Дерево называется идеально сбалансированным, если число узлов в его правом и левом поддеревьях отличается не более чем на единицу (далее будем называть такие деревья сбалансированными). Сбалансированное дерево, состоящее из N узлов, имеет минимальную высоту среди всех бинарных деревьев. Высоту сбалансированного дерева можно определить по формуле:
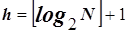 .
.
Минимальная высота при заданном числе узлов достигается, если на всех уровнях, кроме последнего, размещается максимально возможное число узлов. Это происходит за счет равномерного размещения узлов поровну слева и справа от каждого узла.
Правило равномерного размещения для N узлов (правило 1) формулируется с помощью рекурсии:
¨ взять один узел в качестве корня;
¨ по правилу 1 построить левое поддерево с числом узлов nl = N div 2;
¨ по правилу 1 построить правое поддерево с числом узлов nr = N - nl - 1.
Структура сбалансированного дерева из N узлов определяется количеством узлов (рис. 69).
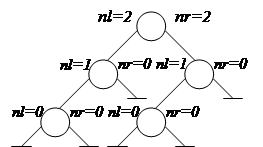 N = 5
N = 5
Рис. 69. Сбалансированное дерево
Процедура построения сбалансированного дерева из N узлов:
| Type
|
|
| PTree = ^ Tree;
| { тип – указатель на узел сбалансированного дерева }
|
| Tree = record
| { тип – элемент хранения узла сбалансированного дерева }
|
| info: char;
|
|
| left, right: PTree
|
|
| end;
|
|
|
|
|
| Procedure Balance(var root: PTree;
| { root – указатель на корень дерева, }
|
| n: byte);
| { n – количество узлов в дереве }
|
| begin
|
|
| if n = 0 then root:=nil
| { если n = 0, построить пустое дерево }
|
| else begin
|
|
| new(root);
| { создать корень дерева }
|
| write(‘Значение инф. поля‘, i, ‘-го узла дерева = ‘);
|
|
| readln(root^.info);
| { заполнить информационное поле корня }
|
| Balance(root^.left, n div 2);
| { построить левое поддерево}
|
| (*1*) Balance(root^.right, n – n div 2 – 1)
| { построить правое поддерево }
|
| (*2*) end
|
|
| (*3*)end;
|
|
| | | | | |
Таблица 5. Трасса состояний стека при работе процедуры построения сбалансированного дерева
Номер уровня рекур- сии
Знач-я входного парам-ра n
|
Стек
|
Знач-я вых. пар-ра
| Выход
| | Исходное состояние (n,root, (.) возврата)
| Конечное состояние
(n,root, (.) возврата)
| root
| root^.left
| root^.right
| из уровня
|
| 1
| 3
| (-, -, -)
| (3,^A, *1*)
| ^A
| -
| -
| -
|
| 2
| 1
|
(3,^A, *1*)
| (1, ^B, *1*)
(3, ^A, *1*)
| ^B
| -
| -
| -
|
| 3
| 0
|
(1, ^B, *1*)
(3, ^A, *1*)
| (0,NIL,*1*)
(1, ^B, *1*)
(3, ^A, *1*)
| NIL
| -
| -
| -
|
|
| 0
| (0,NIL,*1*)
(1, ^B, *1*)
(3, ^A, *1*)
|
(1, ^B, *1*)
(3, ^A, *1*)
| NIL
| -
| -
| (* 3 *)
|
| 2
| 1
| (1, ^B, *1*)
(3, ^A, *1*)
| (1, ^B, *2*)
(3, ^A, *1*)
| ^B
| NIL
| -
| -
|
|
3
| 0
|
(1, ^B, *2*)
(3, ^A, *1*)
| (0,NIL,*2*)
(1, ^B, *2*)
(3, ^A, *1*)
| NIL
| -
| -
| -
|
|
| 0
| (0,NIL,*2*)
(1, ^B, *2*)
(3, ^A, *1*)
|
(1, ^B, *2*)
(3, ^A, *1*)
| NIL
| -
| -
| (* 3 *)
|
| 2
| 1
| (1, ^B, *2*)
(3, ^A, *1*)
|
(3, ^A, *1*)
| ^B
| NIL
| NIL
| (* 3 *)
|
| 1
| 3
| (3, ^A, *1*)
| (3, ^A, *2*)
| ^A
| ^B
| -
| -
|
| 2
| 1
|
(3,^A, *2*)
| (1, ^С, *1*)
(3, ^A, *2*)
| ^C
| -
| -
| -
|
| 3
| 0
|
(1, ^С, *1*)
(3, ^A, *2*)
| (0,NIL,*1*)
(1, ^С, *1*)
(3, ^A, *2*)
| NIL
| -
| -
| -
|
| 0
| (0,NIL,*1*)
(1, ^С, *1*)
(3, ^A, *2*)
|
(1, ^С, *1*)
(3, ^A, *2*)
| NIL
| -
| -
| (* 3 *)
|
| 2
| 1
| (1, ^С, *1*)
(3, ^A, *2*)
| (1, ^С, *2*)
(3, ^A, *2*)
| ^C
| NIL
|
|
|
| 3
| 0
|
(1, ^С, *2*)
(3, ^A, *2*)
| (0,NIL,*2*)
(1, ^С, *2*)
(3, ^A, *2*)
| NIL
| -
| -
| -
|

| 0
| (0,NIL,*2*)
(1, ^С, *2*)
(3, ^A, *2*)
|
(1, ^С, *2*)
(3, ^A, *2*)
| NIL
| -
| -
| (* 3 *)
|
 2 2
| 1
| (1, ^С, *2*)
(3, ^A, *2*)
|
(3, ^A, *2*)
| ^C
| NIL
| NIL
| (* 3 *)
|
| 1
| 3
| (3, ^A, *2*)
| (-, -, -)
| ^A
| ^B
| ^C
| (* 3 *)
|
Для иллюстрации работы этой процедуры и построения трассы состояний стека будем использовать следующие обозначения:
^A – адрес узла дерева, в информационном поле которого хранится символ “A”;
(* 1 *) и (* 2 *) – адреса возврата из уровня рекурсивной процедуры, номер которой на 1 больше текущего;
(* 3 *) – адрес возврата из рекурсивной процедуры текущего уровня.
Трасса построения сбалансированного дерева, содержащего 3 узла, приведена в таблице 5.
Сбалансированное дерево, как и дерево любого другого вида, можно построить в процессе нисходящего обхода. Особенность работы процедуры построения дерева заключается в том, что сначала создаются корневые узлы, адреса которых запоминаются в стеке. Установить ссылки из корневых узлов дерева на их поддеревья можно только после того, как эти поддеревья будут созданы и адреса их корневых узлов возвращены в точки вызова. Точками вызова являются поля ссылок на левое поддерево (root^.left) или правое поддерево (root^.right) корневого узла (в таблице установка этих ссылочных связей показана стрелками). Подобная возможность обеспечивается за счет того, что указатель на корень дерева является параметром-переменной процедуры.
7.5.2. Дихотомические деревья (деревья поиска)
Бинарные деревья часто используются для представления множества объектов, среди которых идет поиск по уникальному значению некоторого атрибута, называемого ключом. При этом на множестве объектов определенно особое отношение порядка - дихотомия, заключающееся в поэтапном разбиении множества информационных полей объектов на два непересекающихся подмножества. Дихотомическим деревом (деревом поиска) называется бинарное дерево, организованное так, что для каждого узла, имеющего ключ Т, справедливо утверждение о том, что в его левом поддереве содержатся узлы с ключами, меньшими T, а в его правом поддереве содержатся узлы с ключами, большими T.
Описание элемента хранения узла дихотомического дерева:
| Type
|
|
| PDtree = ^ Dtree;
| { тип – указатель на узел дихотомического дерева }
|
| Dtree = record
| { тип – элемент хранения узла дихотомического дерева}
|
| key: word;
| { поле ключа }
|
| info: char;
| { информационное поле }
|
| left, right: PDtree
| { ссылки на поддеревья }
|
| end;
|
|
| Var Root: PDtree;
| { указатель на корень дихотомического дерева }
|
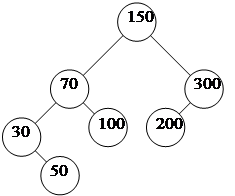
Пример дихотомических деревьев приведен на рис. 70:
а. Несбалансированное б. сбалансированное
Рис. 70. Дихомические деревья
Поиск в дихотомическом дереве узла с заданным значением ключа осуществляется на основе сравнения заданного ключа с ключом корня. Единственное сравнение позволяет перейти к левому или к правому поддереву корня. Если дихотомическое дерево является сбалансированным, то поиск узла с заданным значением ключа требует не более чем [log2 N]+1 сравнений, где N – количество узлов дихотомического дерева. В частном случае, когда множество ключей является линейно упорядоченным, дихотомическое дерево фактически вырождается в линейный список (рис. 71). В этом случае поиск среди N узлов выполняется максимум за N сравнений, а в среднем – за N / 2 сравнений.
Рис. 71. Вырожденное дихотомическое дерево
Структура дихотомического дерева определяется последовательностью задания ключей. Последовательности задания ключей для
¨ дерева рис. а) - 150, 70, 300, 100, 30, 200, 50;
¨ дерева рис. б) - 100, 50, 30, 70, 200, 150, 300;
¨ дерева рис. - 300, 200, 150, 100, 70, 50, 30.
Включение в дихотомическое дерево узла с заданным значением ключа производится следующим образом: если поиск узла привел в тупик (т.е. к пустому поддереву, обозначенному ссылкой со значением NIL), то новый узел необходимо включить в дерево на место пустого поддерева. Таким образом, узел включается в дихотомическое дерево всегда в качестве листа.
| Procedure Ins_Node(var root: PDtree;
| { root – указатель на корень дерева }
|
| k: word);
| { k – ключ вставляемого узла }
|
| begin
|
|
| if root = nil then begin
| { дерево пусто – вставка узла в качестве листа }
|
| new(root);
| { создать элемент хранения узла }
|
| readln(root^. Info);
| { заполнить информационное поле узла }
|
| root^.key:=k;
| { заполнить поле ключа }
|
| root^.left:=nil; root^.right:=nil;
| { заполнить ссылки на поддеревья }
|
| end
|
|
| else
| { дерево не пусто – продолжить поиск: }
|
| if k < root then Ins_Node(root^.left,)
| { поиск в левом поддереве }
|
| else if k > root then Ins_node(root^.right)
| { поиск в правом поддереве}
|
| else writeln(‘узел с ключом’, k, ‘уже есть в дереве’)
| { ключ должен быть }
|
| end;
| { уникальным }
|
| | | | | | | |
Если корневой узел не содержит искомого ключа, процедура рекурсивно вызывает саму себя для продолжения поиска либо в правой, либо в левой половине дерева. В том случае, если достигнут конец ветви и не обнаружен искомый ключ, создается новый узел с этим значением ключа. Рекурсия заканчивается, когда искомый ключ найден (при этом выдается сообщение о невозможности повторного включения узла) или достигнут конец ветви (при этом новый узел включается в дерево).
Какой алгоритм обхода лежит в основе процедуры включения узла в дихотомическое дерево?
При построениидихотомического дерева из N узлов на каждом из N шагов цикла осуществляется вставка узла с заданным значением ключа (вызов процедуры Ins_Node). Поэтому сложность создания дихотомического дерева из N узлов оценивается как N * log2N операций.
При удаленииузла, с заданным значением ключа из дихотомического дерева различают три случая:
1. узла с заданным значением ключа в дереве нет.
2. узел с заданным значением ключа имеет не более одного потомка. В этом случае исключаемый узел заменяется своим потомком.
3. Узел с заданным значением ключа имеет двух потомков. В этом случае исключаемый узел заменяется либо на самый правый узел его левого поддерева, имеющий не более одного потомка, либо на самый левый узел его правого поддерева, имеющий не более одного потомка.
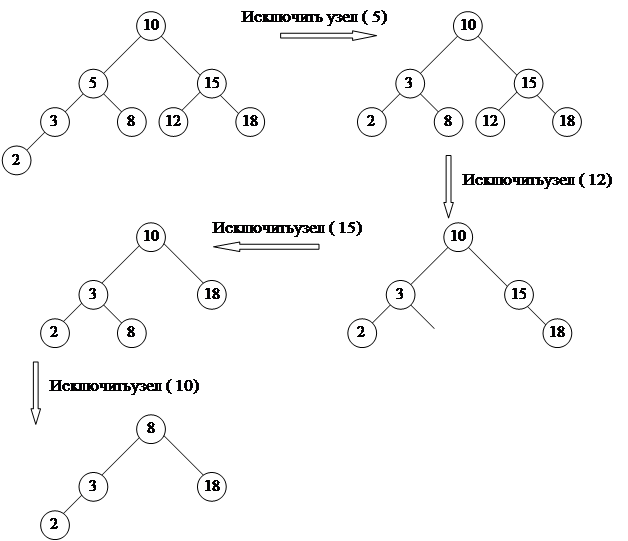
Пример исключения узлов из дихотомического дерева приведен на рис. 72.
Рис. 72. Исключение узлов из дихотомического дерева
Разрушение бинарного дерева любого вида заключается в последовательном освобождении участков памяти, в которых размещены элементы хранения узлов с возвратом их в кучу. В результате разрушения дерево становится пустым.
Какой алгоритм обхода необходимо использовать для разрушения бинарного дерева?
Деревья выражений
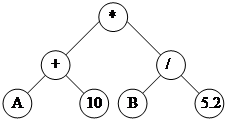
Дерево выражений – бинарное дерево, в корневых узлах которого хранятся признаки операций, а в терминальных узлах – операнды выражения (переменные или константы). Дерево выражений представлено на рис. 73.
Рис. 73. Дерево выражений
Различные алгоритмы обхода дерева выражений соответствуют различной структуре представления выражения в виде строки.
Нисходящему обходу соответствует префиксная форма представления, т. к. в ней знак операции предшествует операнду:
* + А 10. / B 5.2 .
Восходящему обходу соответствует постфиксная форма представления, т. к. в ней знак операции находится после операндов:
A 10. + B 5.2 / *.
Смешанному обходу соответствует инфиксная форма представления, т. к. в ней знак операции находится между операндами:
А + 10. * В / 5.2.
Для того чтобы задать приоритеты операций, используется абсолютно скобочная форма, в которой каждое подвыражение заключается в круглые скобки:
((A + 10.) * (B / 5.2)).
На рис. 74 приведено дерево, смешанный обход которого позволяет получить бесскобочную инфиксную форму, эквивалентную дереву рис. 73, а скобочная инфиксная форма задает совсем другие приоритеты операций. Заметим, что подобная проблема не может возникнуть при использовании префиксной или постфиксной формы представления выражения.
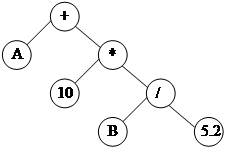 (А + (10. * (В / 5.2)))
(А + (10. * (В / 5.2)))
Рис.. Дерево выражений
Какой алгоритм обхода необходимо использовать для того, чтобы подсчитать значение арифметического выражения, представленного в виде дерева?



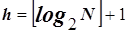 .
. N = 5
N = 5 

 2
2


 (А + (10. * (В / 5.2)))
(А + (10. * (В / 5.2)))


