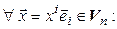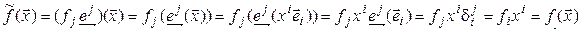(4.31)
(4.31)
пространства 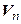 . Обозначим
. Обозначим 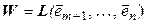 . Очевидно,
. Очевидно,
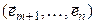 – (4.32)
– (4.32)
базис пространства 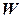 . Докажем, что
. Докажем, что  . Действительно,
. Действительно,
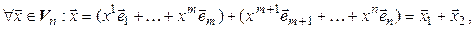
где 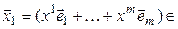
 , а
, а  . Таким образом,
. Таким образом,  . Покажем, что сумма прямая. Пусть
. Покажем, что сумма прямая. Пусть 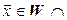
 . Тогда
. Тогда 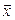 можно разложить как по базису (4.30), так и по базису (4.32):
можно разложить как по базису (4.30), так и по базису (4.32):  и
и  . Получаем
. Получаем
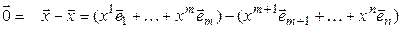 ,
,
откуда в силу линейной независимости (4.31) вытекает, что  . Поэтому
. Поэтому 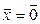 , а значит, сумма действительно прямая.
, а значит, сумма действительно прямая.
Покажем теперь, что 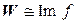 . Построим отображение
. Построим отображение
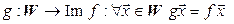 .
.
Очевидно, 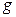 – линейный оператор. Кроме того,
– линейный оператор. Кроме того,  такой, что
такой, что 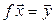 . Так как
. Так как  , то
, то  где
где 
 ,
, 
 . Тогда.
. Тогда. 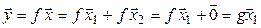 . Таким образом,
. Таким образом, 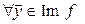
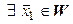 такой, что
такой, что 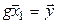 . Предположим, что таких векторов два, т. е. что
. Предположим, что таких векторов два, т. е. что 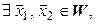
 , но
, но 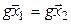 . Имеем
. Имеем
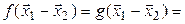
 .
.
Отсюда вытекает, что 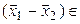
 . Но
. Но 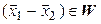 , следовательно,
, следовательно, 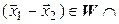
 , и поэтому
, и поэтому 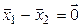 . Итак, мы показали, что
. Итак, мы показали, что  – взаимно однозначное отображение, следовательно, и изоморфизм. Так как изоморфные линейные пространства имеют одинаковые размерности, то
– взаимно однозначное отображение, следовательно, и изоморфизм. Так как изоморфные линейные пространства имеют одинаковые размерности, то 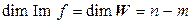 , откуда и вытекает доказываемое утверждение.
, откуда и вытекает доказываемое утверждение.
Рассмотрим теперь тривиальные случаи. Пусть 
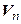 , значит,
, значит, 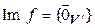 . Тогда
. Тогда 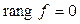 ,
,  . Если же
. Если же 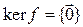 , то
, то  . В обоих случаях равенство (4.29) выполняется. ◄
. В обоих случаях равенство (4.29) выполняется. ◄
Следствие. Если 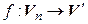 – линейный оператор, то
– линейный оператор, то  (т. е.
(т. е. 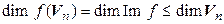 ). Если же оператор
). Если же оператор 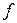 – невырожденный, то
– невырожденный, то 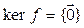 , следовательно,
, следовательно, 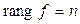 (т. е.
(т. е.  ).
).
Теорема о ранге произведения линейных операторов
Пусть 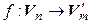 - линейный оператор,
- линейный оператор,
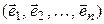 – (4.33)
– (4.33)
базис пространства 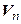 , а
, а
 – (4.34)
– (4.34)
базис пространства  . Аналогично тому, как определялась матрица линейного оператора пространства
. Аналогично тому, как определялась матрица линейного оператора пространства 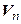 в себя в заданном базисе, определяется и матрица оператора
в себя в заданном базисе, определяется и матрица оператора 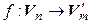 в паре базисов (4.33) и (4.34). Найдем образы векторов базиса (4.33):
в паре базисов (4.33) и (4.34). Найдем образы векторов базиса (4.33):
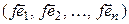 , (4.35)
, (4.35)
каждый из них разложим по базису (4.34), обозначим 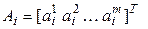 координатный столбец вектора
координатный столбец вектора 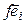 в базисе (4.34),
в базисе (4.34), 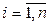 , и составим систему
, и составим систему
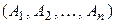 (4.36)
(4.36)
из этих координатных столбцов.
Матрицей линейного оператора 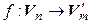 в паре базисов (4.33) и (4.34) называется матрица
в паре базисов (4.33) и (4.34) называется матрица  , составленная из координатных столбцов образов векторов базиса (4.33) в базисе (4.34). Очевидно, эта матрица имеет размеры
, составленная из координатных столбцов образов векторов базиса (4.33) в базисе (4.34). Очевидно, эта матрица имеет размеры  .
.
Нетрудно показать, что при умножении линейных операторов их матрицы в соответствующих парах базисов перемножаются, как это было доказано для случая линейных операторов пространства 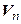 в себя.
в себя.
Теорема 4.11. Пусть 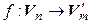 – линейный оператор, A его матрица в паре базисов (4.33) и (4.34). Тогда
– линейный оператор, A его матрица в паре базисов (4.33) и (4.34). Тогда 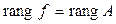 .
.
►В § 3 третьей главы мы показали, что векторы линейно независимы тогда и только тогда, когда линейно независимы их координатные столбцы в некотором базисе. Поэтому максимальное число линейно независимых элементов в системах (4.35) и (4.36) будет одинаковым. Обозначим это число  .
.
Так каккаждый из векторов 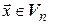 можно разложить по базису (4.33), то
можно разложить по базису (4.33), то 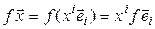 . Следовательно,
. Следовательно, 
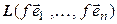 . Тогда
. Тогда
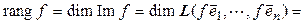 [теорема 3.5] =
[теорема 3.5] =  =
=
= [теорема 3.6] = 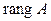 .◄
.◄
Следствие. Если 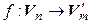 – изоморфизм, то матрица A –невырождена.
– изоморфизм, то матрица A –невырождена.
Теорема 4.12. Пусть 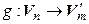 и
и  – линейные операторы. Тогда
– линейные операторы. Тогда  , причем если один из операторов – изоморфизм, то ранг произведения равен рангу второго оператора.
, причем если один из операторов – изоморфизм, то ранг произведения равен рангу второго оператора.
► Обозначим 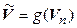 . Нетрудно убедиться, что
. Нетрудно убедиться, что  – подпространство пространства
– подпространство пространства 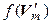 , и поэтому
, и поэтому 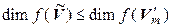 . Тогда
. Тогда
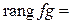
 =
=  ;
;
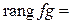
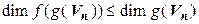 =
= 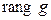 .
.
Кроме того, если  – изоморфизм, то
– изоморфизм, то
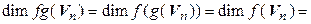
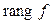 .
.
Если же 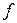 – изоморфизм, то
– изоморфизм, то
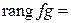
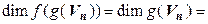
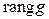 .◄
.◄
Следствие. Ранг произведения матриц не превосходит ранга каждого из сомножителей. Причем, если один из сомножителей – матрица невырожденная, то ранг произведения равен рангу второго сомножителя.
Линейные формы
Определение.Линейной формой на линейном пространстве 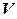 над полем
над полем 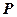 называется линейный оператор
называется линейный оператор 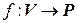 .
.
Мы уже знаем, что множество 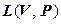 всех линейных форм на линейном пространстве
всех линейных форм на линейном пространстве 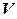 также является линейным пространством над тем же полем, что и
также является линейным пространством над тем же полем, что и 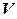 , относительно операций сложения линейных форм и умножения линейной формы на число. Пространство
, относительно операций сложения линейных форм и умножения линейной формы на число. Пространство 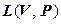 будем называть сопряженным пространству
будем называть сопряженным пространству 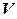 , и обозначать
, и обозначать 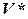 , его элементы назовем ковекторами и тоже для удобства отметим стрелками, но снизу (например,
, его элементы назовем ковекторами и тоже для удобства отметим стрелками, но снизу (например, 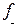 ).
).
Рассмотрим 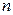 -мерное линейное пространство
-мерное линейное пространство 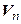 и выберем в нем какой-либо базис:
и выберем в нем какой-либо базис:
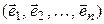 . (4.37)
. (4.37)
Пусть 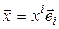 – произвольный вектор пространства
– произвольный вектор пространства 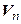 ,
, 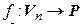 – линейная форма. Тогда
– линейная форма. Тогда
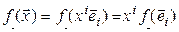 . (4.38)
. (4.38)
Мы видим, что значение линейной формы для вектора 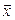 зависит от его координат и некоторых чисел
зависит от его координат и некоторых чисел 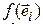 , вовсе с вектором
, вовсе с вектором 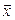 не связанных. Обозначим
не связанных. Обозначим 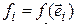 и назовем эти числа компонентами формы
и назовем эти числа компонентами формы 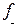 в базисе (4.37). Теперь (4.38) можно переписать и так:
в базисе (4.37). Теперь (4.38) можно переписать и так: 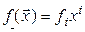 .
.
Выберем в 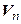 ещё один базис
ещё один базис
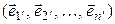 (4.39)
(4.39)
и обозначим 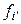 компоненты линейной формы
компоненты линейной формы 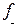 в базисе (4.39).Тогда
в базисе (4.39).Тогда
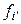 =
= 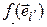 = [определение матрицы перехода] =
= [определение матрицы перехода] = 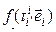 =
=
= [линейность 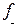 ] =
] = 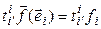 .
.
Мы получили закон изменения компонент линейной формы при изменении базиса.
В пространстве линейных форм 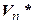 выберем
выберем 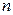 линейных форм
линейных форм
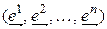 (4.40)
(4.40)
по следующему принципу:
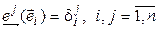 ,
,
т. е. форма 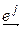 принимает значение, равное 0, для всех базисных векторов, за исключением одного,
принимает значение, равное 0, для всех базисных векторов, за исключением одного, 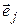 , для которого она принимает значение, равное 1. Существование таких форм вытекает из теоремы 4.1. Докажем линейную независимость (4.40). Как обычно, составим линейную комбинацию и приравняем ее нейтральному элементу.
, для которого она принимает значение, равное 1. Существование таких форм вытекает из теоремы 4.1. Докажем линейную независимость (4.40). Как обычно, составим линейную комбинацию и приравняем ее нейтральному элементу.
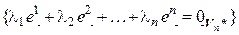
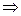
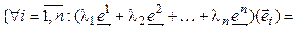
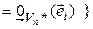
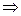
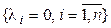
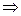 {(4.40) линейно независима}.
{(4.40) линейно независима}.
Пусть теперь 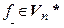 – произвольная линейная форма,
– произвольная линейная форма, 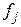 – ее компоненты в базисе (4.40). Обозначим
– ее компоненты в базисе (4.40). Обозначим 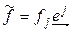 . Тогда
. Тогда 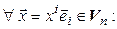
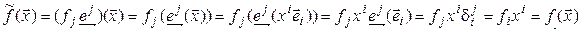
Таким образом, 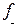 =
= 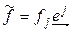 , следовательно, система (4.40) в пространстве
, следовательно, система (4.40) в пространстве 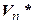 является системой образующих, а значит, и базисом. Итак, пространство, сопряженное к конечномерному линейному пространству, имеет ту же размерность. Базисы (4.37) и (4.40) пространств
является системой образующих, а значит, и базисом. Итак, пространство, сопряженное к конечномерному линейному пространству, имеет ту же размерность. Базисы (4.37) и (4.40) пространств 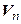 и
и 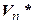 называются сопряженными или взаимными. Следовательно, компоненты линейной формы
называются сопряженными или взаимными. Следовательно, компоненты линейной формы 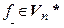 в базисе (4.37) пространства
в базисе (4.37) пространства 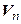 – это её координаты во взаимном базисе пространства
– это её координаты во взаимном базисе пространства 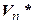 .
.



 (4.31)
(4.31)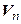 . Обозначим
. Обозначим 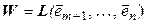 . Очевидно,
. Очевидно,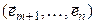 – (4.32)
– (4.32)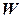 . Докажем, что
. Докажем, что  . Действительно,
. Действительно,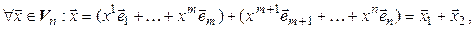
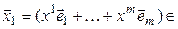
 , а
, а  . Таким образом,
. Таким образом,  . Покажем, что сумма прямая. Пусть
. Покажем, что сумма прямая. Пусть 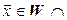
 . Тогда
. Тогда 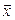 можно разложить как по базису (4.30), так и по базису (4.32):
можно разложить как по базису (4.30), так и по базису (4.32):  и
и  . Получаем
. Получаем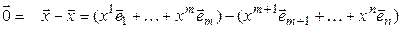 ,
, . Поэтому
. Поэтому 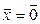 , а значит, сумма действительно прямая.
, а значит, сумма действительно прямая.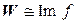 . Построим отображение
. Построим отображение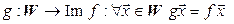 .
.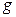 – линейный оператор. Кроме того,
– линейный оператор. Кроме того,  такой, что
такой, что 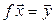 . Так как
. Так как  где
где 
 ,
, 
 . Тогда.
. Тогда. 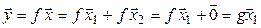 . Таким образом,
. Таким образом, 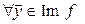
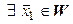 такой, что
такой, что 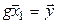 . Предположим, что таких векторов два, т. е. что
. Предположим, что таких векторов два, т. е. что 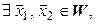
 , но
, но 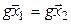 . Имеем
. Имеем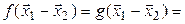
 .
.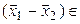
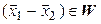 , следовательно,
, следовательно, 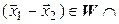
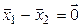 . Итак, мы показали, что
. Итак, мы показали, что  – взаимно однозначное отображение, следовательно, и изоморфизм. Так как изоморфные линейные пространства имеют одинаковые размерности, то
– взаимно однозначное отображение, следовательно, и изоморфизм. Так как изоморфные линейные пространства имеют одинаковые размерности, то 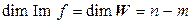 , откуда и вытекает доказываемое утверждение.
, откуда и вытекает доказываемое утверждение.
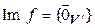 . Тогда
. Тогда 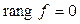 ,
,  . Если же
. Если же 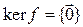 , то
, то  . В обоих случаях равенство (4.29) выполняется. ◄
. В обоих случаях равенство (4.29) выполняется. ◄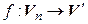 – линейный оператор, то
– линейный оператор, то  (т. е.
(т. е. 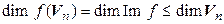 ). Если же оператор
). Если же оператор 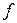 – невырожденный, то
– невырожденный, то 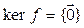 , следовательно,
, следовательно, 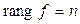 (т. е.
(т. е.  ).
).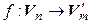 - линейный оператор,
- линейный оператор,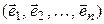 – (4.33)
– (4.33) – (4.34)
– (4.34) . Аналогично тому, как определялась матрица линейного оператора пространства
. Аналогично тому, как определялась матрица линейного оператора пространства 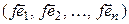 , (4.35)
, (4.35)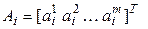 координатный столбец вектора
координатный столбец вектора 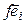 в базисе (4.34),
в базисе (4.34), 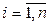 , и составим систему
, и составим систему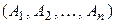 (4.36)
(4.36) , составленная из координатных столбцов образов векторов базиса (4.33) в базисе (4.34). Очевидно, эта матрица имеет размеры
, составленная из координатных столбцов образов векторов базиса (4.33) в базисе (4.34). Очевидно, эта матрица имеет размеры  .
.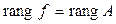 .
. .
.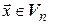 можно разложить по базису (4.33), то
можно разложить по базису (4.33), то 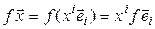 . Следовательно,
. Следовательно, 
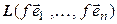 . Тогда
. Тогда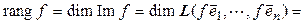 [теорема 3.5] =
[теорема 3.5] = 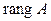 .◄
.◄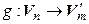 и
и  – линейные операторы. Тогда
– линейные операторы. Тогда  , причем если один из операторов – изоморфизм, то ранг произведения равен рангу второго оператора.
, причем если один из операторов – изоморфизм, то ранг произведения равен рангу второго оператора.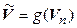 . Нетрудно убедиться, что
. Нетрудно убедиться, что  – подпространство пространства
– подпространство пространства 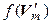 , и поэтому
, и поэтому 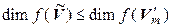 . Тогда
. Тогда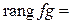
 =
=  ;
;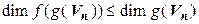 =
= 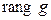 .
. – изоморфизм, то
– изоморфизм, то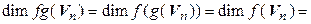
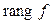 .
.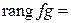
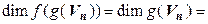
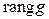 .◄
.◄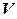 над полем
над полем 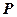 называется линейный оператор
называется линейный оператор 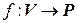 .
.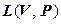 всех линейных форм на линейном пространстве
всех линейных форм на линейном пространстве 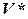 , его элементы назовем ковекторами и тоже для удобства отметим стрелками, но снизу (например,
, его элементы назовем ковекторами и тоже для удобства отметим стрелками, но снизу (например, 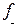 ).
).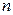 -мерное линейное пространство
-мерное линейное пространство 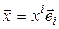 – произвольный вектор пространства
– произвольный вектор пространства 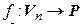 – линейная форма. Тогда
– линейная форма. Тогда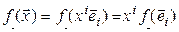 . (4.38)
. (4.38)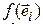 , вовсе с вектором
, вовсе с вектором 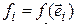 и назовем эти числа компонентами формы
и назовем эти числа компонентами формы 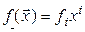 .
.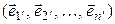 (4.39)
(4.39)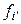 компоненты линейной формы
компоненты линейной формы 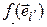 = [определение матрицы перехода] =
= [определение матрицы перехода] = 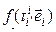 =
=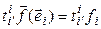 .
.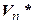 выберем
выберем 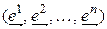 (4.40)
(4.40)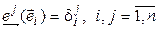 ,
, 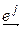 принимает значение, равное 0, для всех базисных векторов, за исключением одного,
принимает значение, равное 0, для всех базисных векторов, за исключением одного, 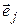 , для которого она принимает значение, равное 1. Существование таких форм вытекает из теоремы 4.1. Докажем линейную независимость (4.40). Как обычно, составим линейную комбинацию и приравняем ее нейтральному элементу.
, для которого она принимает значение, равное 1. Существование таких форм вытекает из теоремы 4.1. Докажем линейную независимость (4.40). Как обычно, составим линейную комбинацию и приравняем ее нейтральному элементу.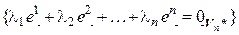
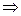
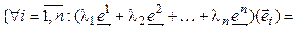
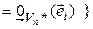
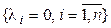
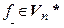 – произвольная линейная форма,
– произвольная линейная форма, 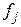 – ее компоненты в базисе (4.40). Обозначим
– ее компоненты в базисе (4.40). Обозначим 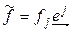 . Тогда
. Тогда