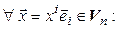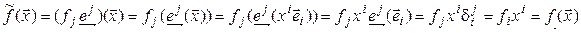ГЛАВА 4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
Понятие отображения
Пусть Х и Y – множества элементов произвольной природы. Говорят, что задано отображение 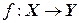 (читается: отображение f множества X во множество Y), если задан закон, по которому каждому элементу
(читается: отображение f множества X во множество Y), если задан закон, по которому каждому элементу 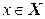 ставится в соответствие вполне определенный элемент
ставится в соответствие вполне определенный элемент 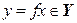 (рис. 4.1).
(рис. 4.1).
Рис. 4.1
Если 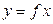 , то
, то 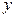 называется образом элемента
называется образом элемента 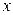 ;
; 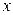 – прообразом элемента
– прообразом элемента 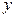 при отображении f.
при отображении f.
 Примерами отображений являются функции, которые изучаются в школьном курсе математики и в математическом анализе, например, функция
Примерами отображений являются функции, которые изучаются в школьном курсе математики и в математическом анализе, например, функция 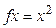 – отображение
– отображение 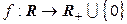 . Классный журнал является примером отображения множества учеников в классе во множество всех фамилий.
. Классный журнал является примером отображения множества учеников в классе во множество всех фамилий.
Отображение 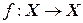 называется тождественным, если оно любой элемент оставляет на месте. Тождественное отображение множества X на себя будем обозначать
называется тождественным, если оно любой элемент оставляет на месте. Тождественное отображение множества X на себя будем обозначать 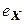 . Таким образом,
. Таким образом, 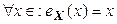 .
.
Отображение 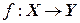 называется взаимно однозначным (или биективным, или биекцией), если оно удовлетворяет двум условиям:
называется взаимно однозначным (или биективным, или биекцией), если оно удовлетворяет двум условиям:
1. 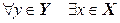 такой, что
такой, что 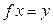 .
.
2. 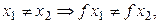
или одному, эквивалентному им, третьему условию:
3. 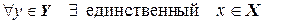 такой, что
такой, что 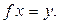
Хороший пример взаимно однозначного отображения: в театре дают билет, каждому билету соответствует некоторое кресло, причем только одно.
Отображения 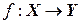 и
и 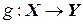 называются равными, если
называются равными, если 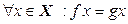 .
.
Пусть заданы отображения 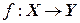 и
и 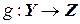 . Произведением (или композицией) отображений f и g называется отображение
. Произведением (или композицией) отображений f и g называется отображение 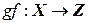 такое, что
такое, что 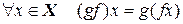 (рис. 4.2).
(рис. 4.2).
Рис. 4.2
Замечание. В произведении отображений сначала действует внутреннее, а затем внешнее отображение.
Примером произведения отображений является сложная функция.
Лемма 4.1. Произведение отображений ассоциативно, т. е. если заданы отображения 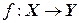 ,
, 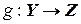 и
и 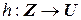 , то
, то
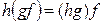 .
.
uДля доказательства равенства отображений 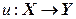 и
и 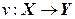 нужно показать, что
нужно показать, что 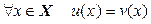 .
.
Итак, выберем произвольное 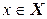 . Тогда
. Тогда
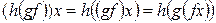 ; (4.1)
; (4.1)
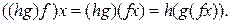 (4.2)
(4.2)
Сравнивая (4.1) и (4.2), видим, что 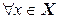 :
: 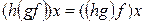 и поэтому,
и поэтому, 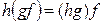 .t
.t
Отображение 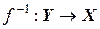 называется обратным к отображению
называется обратным к отображению 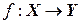 , если
, если 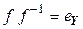 и
и 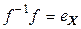 (рис. 4.3).
(рис. 4.3).
Рис. 4.3
Упражнение. Докажите следующие утверждения
1. Для того чтобы отображение f имело обратное, необходимо и достаточно, чтобы f было взаимно однозначным.
2. Если отображение имеет обратное, то это обратное определяется однозначно.
Определение линейного оператора
И его простейшие свойства
Определение. Пусть 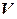 и
и 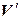 – линейные пространства над одним и тем же полем
– линейные пространства над одним и тем же полем 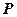 . Отображение
. Отображение 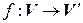 называется линейным оператором, если оно удовлетворяет следующим условиям:
называется линейным оператором, если оно удовлетворяет следующим условиям:
1*. 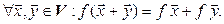
2*. 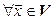
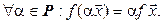
Следствие. При линейном операторе образ линейной комбинации векторов равен такой же линейной комбинации их образов, т. е. если 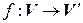 – линейный оператор, то
– линейный оператор, то 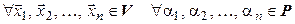 :
:
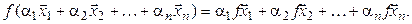 (4.3)
(4.3)
uДоказательство проведем методом математической индукции по количеству векторов.
а) n = 1: 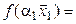 [2*]
[2*] 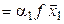 – истинно.
– истинно.
б) Предполагая, что утверждение верно для (n -1)-го вектора, доказываем его для n векторов.
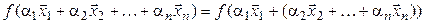 = [1*] =
= [1*] =
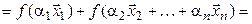 [2* и предположение индукции] =
[2* и предположение индукции] =
= 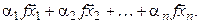 t
t
Примеры линейных операторов
1. Нулевой оператор 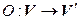 :
: 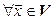
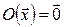 . Очевидно, этот оператор удовлетворяет условиям 1* и 2*, значит, является линейным.
. Очевидно, этот оператор удовлетворяет условиям 1* и 2*, значит, является линейным.
2. Тождественный оператор 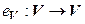 также, очевидно, является линейным.
также, очевидно, является линейным.
3. Оператор дифференцирования 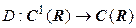 , который каждой дифференцируемой функции ставит в соответствие ее производную, является линейным, так как производная суммы функций равна сумме их производных, а при умножении функции на число ее производная умножается на это число.
, который каждой дифференцируемой функции ставит в соответствие ее производную, является линейным, так как производная суммы функций равна сумме их производных, а при умножении функции на число ее производная умножается на это число.
4. Пусть 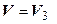 – пространство свободных векторов,
– пространство свободных векторов, 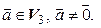
Покажем, что оператор проектирования на ось 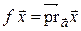 является линейным.
является линейным.
►В аналитической геометрии доказывалось, что 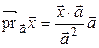 . Тогда
. Тогда
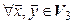 :
: 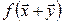 =
= 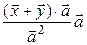 =
= 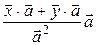 =
= 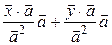 =
= 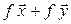 ;
;
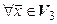
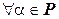 :
: 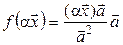 =
= 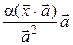 =
= 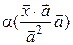 =
= 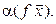
Таким образом, условия 1* и 2* выполняются, а значит, оператор проектирования вектора на ось является линейным.◄
 5. В пространстве
5. В пространстве 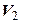 векторов плоскости, закрепленных в начале координат О, рассмотрим оператор
векторов плоскости, закрепленных в начале координат О, рассмотрим оператор 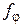 поворота вектора на угол
поворота вектора на угол 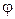 против часовой стрелки и докажем его линейность.
против часовой стрелки и докажем его линейность.
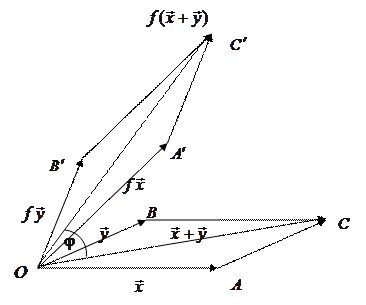
► Пусть 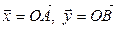 – произвольные векторы,
– произвольные векторы,
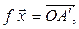
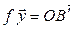 (рис. 4.4),
(рис. 4.4), 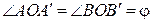 . Построим
. Построим 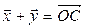 и
и 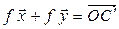 по правилу параллелограмма. Так как плоскость поворачивается
по правилу параллелограмма. Так как плоскость поворачивается
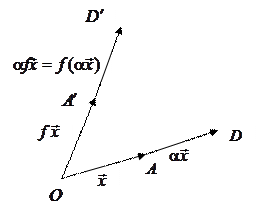 Рис.4.4 как жесткое целое, методами элементарной геометрии нетрудно показать, что при этом повороте диагональ
Рис.4.4 как жесткое целое, методами элементарной геометрии нетрудно показать, что при этом повороте диагональ 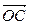 переходит в диагональ
переходит в диагональ 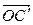 . Значит,
. Значит, 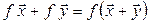 .
.
Пусть
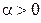
,
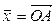
,
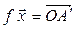
,
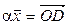
,
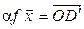
(рис.4.5). Очевидно, вектор
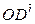
получен из
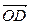
поворотом на угол
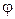
, следовательно,
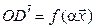
, а значит,
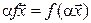
. Аналогично это свойство проверяется и при
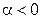
, а при
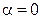
оно очевидно.◄
Теорема 4.1. Пусть 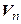 и
и 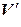 – линейные пространства над одним и тем же полем P и пусть в пространстве
– линейные пространства над одним и тем же полем P и пусть в пространстве 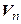 задан базис
задан базис
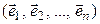 , (4.4)
, (4.4)
а в пространстве 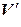 – произвольная система векторов
– произвольная система векторов
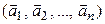 . (4.5)
. (4.5)
Тогда существует единственный линейный оператор 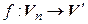 , переводящий базис (4.4) в систему (4.5), то есть такой, что
, переводящий базис (4.4) в систему (4.5), то есть такой, что
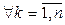 :
: 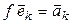 . (4.6)
. (4.6)
► Построение. Выберем произвольный вектор 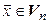 и разложим его по базису (4.4):
и разложим его по базису (4.4): 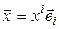 . Положим по определению
. Положим по определению
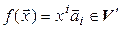 .
.
Линейность. Если 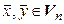 – произвольные векторы,
– произвольные векторы, 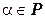 , то
, то 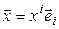 ,
, 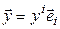 ,
, 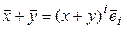
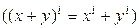 ,
, 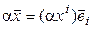 . Тогда
. Тогда
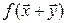 = [определение f ] =
= [определение f ] = 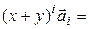
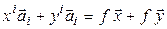 ;
;
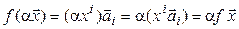 .
.
Выполнение (4.6). Заметим, что все координаты вектора 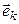 в базисе (4.3) равны нулю, за исключением k -й, которая равна 1. Таким образом, i -я координата вектора
в базисе (4.3) равны нулю, за исключением k -й, которая равна 1. Таким образом, i -я координата вектора 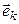 равна
равна 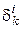 , то есть
, то есть 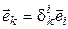 . Тогда
. Тогда
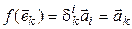 ,
,
значит, условие (4.6) выполнено.
Единственность. Предположим, что существует еще один линейный оператор 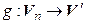 ,
, 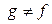 , переводящий (4.4) в (4.5), то есть такой, что
, переводящий (4.4) в (4.5), то есть такой, что 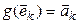 . Тогда
. Тогда 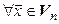 :
: 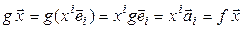 – противоречие.◄
– противоречие.◄
Матрица линейного оператора
Примеры
1. Матрицей нулевого оператора 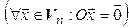 в любом базисе является нулевая матрица; матрицей тождественного оператора
в любом базисе является нулевая матрица; матрицей тождественного оператора 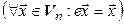 также в любом базисе является матрица единичная.
также в любом базисе является матрица единичная.
2. Пусть 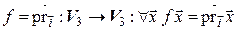 . Составим матрицу оператора проектирования на ось O x в базисе
. Составим матрицу оператора проектирования на ось O x в базисе 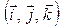 . Для этого находим образы базисных векторов и разлагаем их по базису:
. Для этого находим образы базисных векторов и разлагаем их по базису:
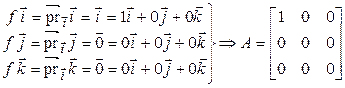 .
.
3. Составим матрицу оператора 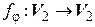 поворота плоскости на угол
поворота плоскости на угол  (см. § 2) в базисе
(см. § 2) в базисе 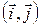 . Из рис. 4.5 и 4.6 видно, что
. Из рис. 4.5 и 4.6 видно, что
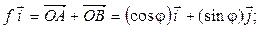
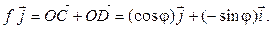
Тогда
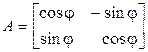 .
.
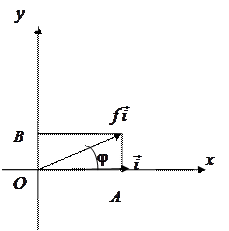
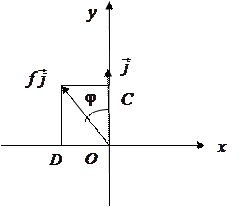
Рис. 4.5 Рис. 4.6
Итак, если в пространстве  задан какой-либо базис, то каждому линейному оператору
задан какой-либо базис, то каждому линейному оператору  можно поставить в соответствие его матрицу в этом базисе, т. е. квадратную матрицу A n- го порядка, причем эта матрица определяется однозначно.
можно поставить в соответствие его матрицу в этом базисе, т. е. квадратную матрицу A n- го порядка, причем эта матрица определяется однозначно.
Пусть теперь задана квадратная матрица А с элементами из поля P. Обозначим 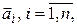 вектор, координатный столбец которого в базисе (4.8) совпадает с i -м столбцом матрицы А. Получим упорядоченную систему векторов
вектор, координатный столбец которого в базисе (4.8) совпадает с i -м столбцом матрицы А. Получим упорядоченную систему векторов
(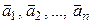 )
)
Согласно теореме 4.1, существует единственный линейный оператор 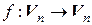 такой, что
такой, что 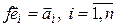 . По определению матрица этого оператора в базисе (4.8) совпадает с А.
. По определению матрица этого оператора в базисе (4.8) совпадает с А.
Обозначим 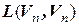 – множество всех линейных операторов линейного пространства
– множество всех линейных операторов линейного пространства 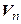 над полем Р в себя. Из вышесказанного вытекает: если в
над полем Р в себя. Из вышесказанного вытекает: если в 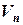 задан базис, то определяется отображение
задан базис, то определяется отображение
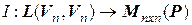 ,
,
которое ставит в соответствие каждому линейному оператору 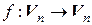 его матрицу в этом базисе, причем это отображение взаимно однозначно. Это дает возможность в конечномерных линейных пространствах линейные операторы изучать с помощью их матриц.
его матрицу в этом базисе, причем это отображение взаимно однозначно. Это дает возможность в конечномерных линейных пространствах линейные операторы изучать с помощью их матриц.
При изменении базиса
Теорема 4.2. Пусть в линейном пространстве 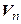 заданы два базиса:
заданы два базиса:
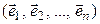 (4.16)
(4.16)
и
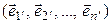 , (4.17)
, (4.17)
и пусть A = 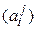 и
и 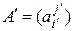 – матрицы линейного оператора
– матрицы линейного оператора 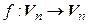 в базисах (4.16) и (4.17) соответственно. Тогда
в базисах (4.16) и (4.17) соответственно. Тогда
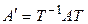 , (4.18)
, (4.18)
где Т – матрица перехода от (4.16) к (4.17).
►Чтобы найти матрицу 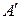 , следует образы векторов базиса (4.17) разложить опять же по этому базису. Имеем
, следует образы векторов базиса (4.17) разложить опять же по этому базису. Имеем
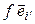 = [определение матрицы перехода] =
= [определение матрицы перехода] = 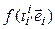 = [(4.3)] =
= [(4.3)] = 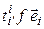 =
=
= [(4.11)] = 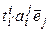 = [свойство 6º § 9 гл. 3] =
= [свойство 6º § 9 гл. 3] = 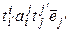 .
.
Итак,
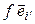 =
= 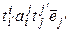 . (4.19)
. (4.19)
Равенство (4.19) задает разложение вектора 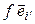 по базису (4.17). С другой стороны, по определению матрицы линейного оператора,
по базису (4.17). С другой стороны, по определению матрицы линейного оператора,
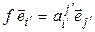 . (4.20)
. (4.20)
В силу единственности координат вектора в данном базисе из (4.19) и (4.20) получаем равенство
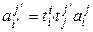 , (4.21)
, (4.21)
которое и дает нам связь элементов матриц линейного оператора в различных базисах. Запишем (4.21) по правилу цепочки:
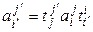 . (4.22)
. (4.22)
Так как 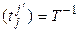 (см. замечание в § 9 гл. 3), то из (4.22) получаем (4.18).◄
(см. замечание в § 9 гл. 3), то из (4.22) получаем (4.18).◄
Определение. Квадратные матрицы 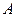 и
и 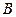 называются подобными, если существует невырожденная матрица Т такая, что
называются подобными, если существует невырожденная матрица Т такая, что 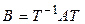 .
.
Таким образом, мы видим, что матрицы линейного оператора в различных базисах подобны.
Лемма 4.1. 1. Подобные матрицы имеют одинаковые определители.
2. Если невырожденные квадратные матрицы подобны, то обратные к ним тоже подобны, причем подобие осуществляется при помощи одной и той же матрицы,
►1. 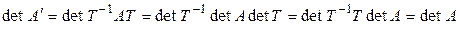 .
.
2. Пусть матрицы 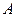 и
и 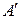 подобны и пусть подобие осуществляется при помощи матрицы
подобны и пусть подобие осуществляется при помощи матрицы 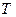 . Покажем, что матрица
. Покажем, что матрица 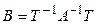 , подобная матрице
, подобная матрице 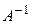 , является обратной к
, является обратной к 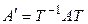 . Действительно,
. Действительно, 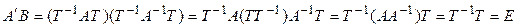 .◄
.◄
Определение. Определителем линейного оператора 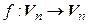 называется определитель его матрицы в некотором, а значит, и в любом базисе пространства
называется определитель его матрицы в некотором, а значит, и в любом базисе пространства 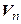 .
.
Линейного оператора
Пусть 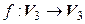 – линейный оператор,
– линейный оператор, 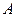 – его матрица в некотором ортонормированном базисе
– его матрица в некотором ортонормированном базисе 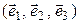 , и пусть
, и пусть 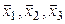 – некомпланарные векторы, а
– некомпланарные векторы, а 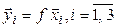 – их образы. Обозначим
– их образы. Обозначим 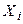 и
и 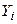 координатные столбцы в выбранном базисе векторов
координатные столбцы в выбранном базисе векторов 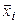 и
и 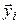 соответственно,
соответственно, 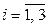 ,
, 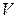 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах 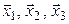 , а
, а 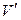 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах 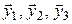 . Тогда, учитывая (4.15), получаем
. Тогда, учитывая (4.15), получаем
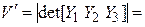 [(4.15) § 3]
[(4.15) § 3] 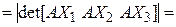 [§ 5 гл. 1] =
[§ 5 гл. 1] =
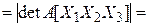 [§ 6 гл. 1]
[§ 6 гл. 1] 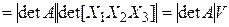 . (4.23)
. (4.23)
Рассмотрим теперь пространство 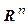 . Выберем в нем точку
. Выберем в нем точку 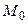 и
и 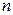 линейно независимых векторов
линейно независимых векторов 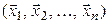 ,
, 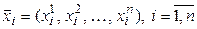 . Параллелепипедом в
. Параллелепипедом в 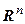 (
(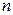 -мерным параллелепипедом) будем называть множество точек в
-мерным параллелепипедом) будем называть множество точек в 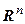
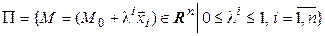 . (4.24)
. (4.24)
Обозначим 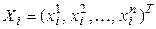 координатный столбец вектора
координатный столбец вектора 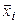 в каноническом базисе. По аналогии с трехмерным пространством, объемом
в каноническом базисе. По аналогии с трехмерным пространством, объемом 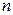 -мерного параллелепипеда (4.24) будем называть число
-мерного параллелепипеда (4.24) будем называть число
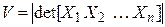 .
.
Можно доказать, что при переходе от одного ортонормированного базиса к другому ортонормированному это число не меняется, т.е. определение объема параллелепипеда является корректным.
Так же, как и для трехмерного пространства, для пространства 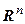 доказывается равенство (4.23).
доказывается равенство (4.23).
Вывод: из формулы (4.23) на основании леммы 4.1 вытекает, что коэффициент изменения объема параллелепипеда при линейном операторе равен модулю определителя этого оператора.
Обратный линейный оператор
Теорема 4.7. Для любого невырожденного линейногооператора 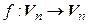 существует единственный обратный оператор
существует единственный обратный оператор 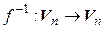 , который также является линейным. При этом, если А – матрица оператора
, который также является линейным. При этом, если А – матрица оператора 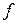 в некотором базисе, то матрица оператора
в некотором базисе, то матрица оператора 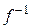 в том же базисе совпадает с матрицей
в том же базисе совпадает с матрицей 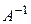 .
.
► Единственность. Пусть некоторый оператор 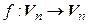 имеет два разных обратных:
имеет два разных обратных: 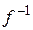 и
и 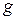 . Тогда
. Тогда
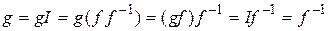
– противоречие.
Существование. Пусть 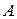 – матрица оператора
– матрица оператора 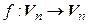 в некотором базисе. Тогда, по теореме 4.4
в некотором базисе. Тогда, по теореме 4.4 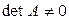 , значит, существует
, значит, существует 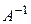 . Обозначим
. Обозначим 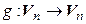 – тот линейный оператор, матрица которого в выбранном базисесовпадаетс
– тот линейный оператор, матрица которого в выбранном базисесовпадаетс 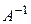 . Так как
. Так как 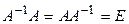 , и так как произведению матриц соответствует произведение операторов, то
, и так как произведению матриц соответствует произведение операторов, то 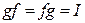 , и, таким образом,
, и, таким образом, 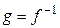 .◄
.◄
Замечание. На основании леммы 4.1 определение обратного линейного оператора не зависит от выбора базиса, т.е. является корректным.
Замечание.===( или упражнение) М ожно доказать, что любой взаимно однозначный линейный оператор 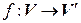 имеет единственный обратный, который тоже является линейным.
имеет единственный обратный, который тоже является линейным.
Свойства изоморфизма
1. 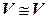 – рефлективность (изоморфизм осуществляет тождественное отображение).
– рефлективность (изоморфизм осуществляет тождественное отображение).
2. 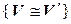

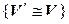 – симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью
– симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью 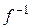 ).
).
3. { 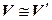 ,
, 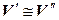 }
} 
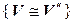 – транзитивность (если первый изоморфизм осуществляется с помощью отображения
– транзитивность (если первый изоморфизм осуществляется с помощью отображения 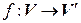 , второй –
, второй – 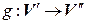 , то третий изоморфизм осуществляется с помощью отображения
, то третий изоморфизм осуществляется с помощью отображения 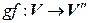 ).
).
Строгого доказательства этих свойств мы не приводим.
Теорема 4.8. Изоморфные линейные пространства имеют одинаковые размерности.
►Пусть 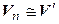 и пусть
и пусть 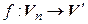 – изоморфизм. Выберем в
– изоморфизм. Выберем в 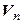 какой-либо базис
какой-либо базис
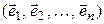 (4.27)
(4.27)
и покажем, что система
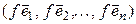 – (4.28)
– (4.28)
базис пространства 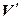 . Действительно, в силу взаимной однозначности f,
. Действительно, в силу взаимной однозначности f, 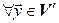
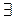 единственный
единственный 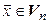 такой, что
такой, что 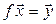 . Тогда, если
. Тогда, если 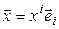 , то
, то 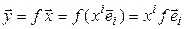 . Значит, (4.28) – система образующих в
. Значит, (4.28) – система образующих в  .
.
Докажем теперь линейную независимость (4.28).
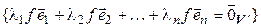
 [линейность f ]
[линейность f ] 

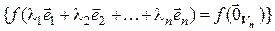
 [взаимная однозначность f ]
[взаимная однозначность f ] 

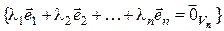
 [линейная независимость (4.27)]
[линейная независимость (4.27)] 

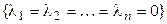
 {(4.28) – линейно независима}.
{(4.28) – линейно независима}.
Таким образом, (4.28) – базис в 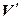 , а значит,
, а значит, 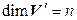 . ◄
. ◄
Теорема 4.9. Все n -мерные линейные пространства над полем Р изоморфны между собой, т. е. существует единственное с точностью до изоморфизма n- мерное линейное пространство над полем Р.
►а) Докажем, что 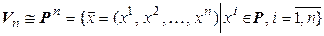 .
.
Выберем в 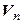 какой-либо базис
какой-либо базис 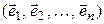 . Тогда
. Тогда 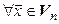 :
: 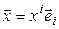 . Обозначим
. Обозначим 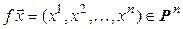 . Очевидно, отображение
. Очевидно, отображение 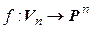 – взаимно однозначное. Кроме того,
– взаимно однозначное. Кроме того, 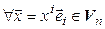 ,
, 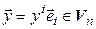 :
:
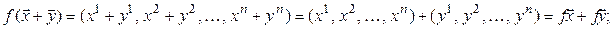
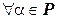
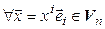 :
: 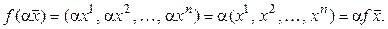
Поэтому f – линейный оператор, а значит, и изоморфизм. Итак, 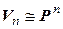 .
.
б) Пусть теперь 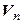 и
и 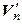 – n- мерные линейные пространства над одним и тем же полем Р. Тогда
– n- мерные линейные пространства над одним и тем же полем Р. Тогда
{ 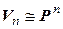 и
и 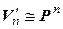 }
}  [симметричность]
[симметричность]  {
{ 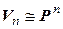 и
и 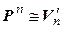 и }
и } 
 [транзитивность]
[транзитивность]  {
{ 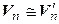 }.◄
}.◄
Таким образом, мы показали, что с точки зрения математики единственным n- мерным линейным пространством над полем Р является 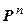 .
.
Линейные формы
Определение.Линейной формой на линейном пространстве 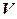 над полем
над полем 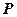 называется линейный оператор
называется линейный оператор 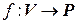 .
.
Мы уже знаем, что множество 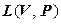 всех линейных форм на линейном пространстве
всех линейных форм на линейном пространстве 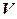 также является линейным пространством над тем же полем, что и
также является линейным пространством над тем же полем, что и 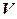 , относительно операций сложения линейных форм и умножения линейной формы на число. Пространство
, относительно операций сложения линейных форм и умножения линейной формы на число. Пространство 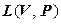 будем называть сопряженным пространству
будем называть сопряженным пространству 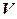 , и обозначать
, и обозначать 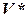 , его элементы назовем ковекторами и тоже для удобства отметим стрелками, но снизу (например,
, его элементы назовем ковекторами и тоже для удобства отметим стрелками, но снизу (например, 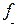 ).
).
Рассмотрим 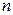 -мерное линейное пространство
-мерное линейное пространство 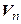 и выберем в нем какой-либо базис:
и выберем в нем какой-либо базис:
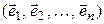 . (4.37)
. (4.37)
Пусть 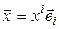 – произвольный вектор пространства
– произвольный вектор пространства 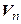 ,
, 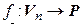 – линейная форма. Тогда
– линейная форма. Тогда
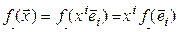 . (4.38)
. (4.38)
Мы видим, что значение линейной формы для вектора 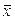 зависит от его координат и некоторых чисел
зависит от его координат и некоторых чисел 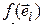 , вовсе с вектором
, вовсе с вектором 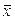 не связанных. Обозначим
не связанных. Обозначим 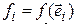 и назовем эти числа компонентами формы
и назовем эти числа компонентами формы 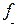 в базисе (4.37). Теперь (4.38) можно переписать и так:
в базисе (4.37). Теперь (4.38) можно переписать и так: 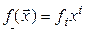 .
.
Выберем в 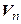 ещё один базис
ещё один базис
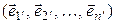 (4.39)
(4.39)
и обозначим 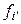 компоненты линейной формы
компоненты линейной формы 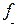 в базисе (4.39).Тогда
в базисе (4.39).Тогда
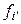 =
= 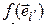 = [определение матрицы перехода] =
= [определение матрицы перехода] = 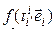 =
=
= [линейность 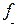 ] =
] = 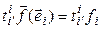 .
.
Мы получили закон изменения компонент линейной формы при изменении базиса.
В пространстве линейных форм 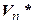 выберем
выберем 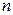 линейных форм
линейных форм
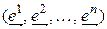 (4.40)
(4.40)
по следующему принципу:
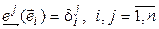 ,
,
т. е. форма 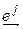 принимает значение, равное 0, для всех базисных векторов, за исключением одного,
принимает значение, равное 0, для всех базисных векторов, за исключением одного, 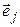 , для которого она принимает значение, равное 1. Существование таких форм вытекает из теоремы 4.1. Докажем линейную независимость (4.40). Как обычно, составим линейную комбинацию и приравняем ее нейтральному элементу.
, для которого она принимает значение, равное 1. Существование таких форм вытекает из теоремы 4.1. Докажем линейную независимость (4.40). Как обычно, составим линейную комбинацию и приравняем ее нейтральному элементу.
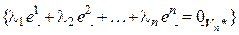

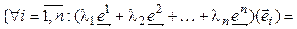
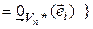

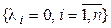
 {(4.40) линейно независима}.
{(4.40) линейно независима}.
Пусть теперь 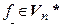 – произвольная линейная форма,
– произвольная линейная форма, 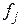 – ее компоненты в базисе (4.40). Обозначим
– ее компоненты в базисе (4.40). Обозначим 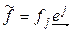 . Тогда
. Тогда 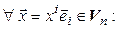
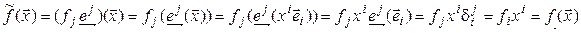
Таким образом, 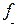 =
= 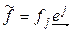 , следовательно, система (4.40) в пространстве
, следовательно, система (4.40) в пространстве 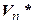 является системой образующих, а значит, и базисом. Итак, пространство, сопряженное к конечномерному линейному пространству, имеет ту же размерность. Базисы (4.37) и (4.40) пространств
является системой образующих, а значит, и базисом. Итак, пространство, сопряженное к конечномерному линейному пространству, имеет ту же размерность. Базисы (4.37) и (4.40) пространств 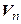 и
и 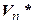 называются сопряженными или взаимными. Следовательно, компоненты линейной формы
называются сопряженными или взаимными. Следовательно, компоненты линейной формы 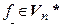 в базисе (4.37) пространства
в базисе (4.37) пространства 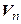 – это её координаты во взаимном базисе пространства
– это её координаты во взаимном базисе пространства 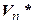 .
.
ГЛАВА 4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
Понятие отображения
Пусть Х и Y – множества элементов произвольной природы. Говорят, что задано отображение 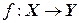 (читается: отображение f множества X во множество Y), если задан закон, по которому каждому элементу
(читается: отображение f множества X во множество Y), если задан закон, по которому каждому элементу 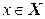 ставится в соответствие вполне определенный элемент
ставится в соответствие вполне определенный элемент 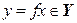 (рис. 4.1).
(рис. 4.1).
Рис. 4.1
Если 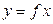 , то
, то 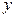 называется образом элемента
называется образом элемента 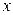 ;
; 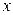 – прообразом элемента
– прообразом элемента 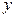 при отображении f.
при отображении f.
 Примерами отображений являются функции, которые изучаются в школьном курсе математики и в математическом анализе, например, функция
Примерами отображений являются функции, которые изучаются в школьном курсе математики и в математическом анализе, например, функция 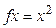 – отображение
– отображение 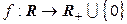 . Классный журнал является примером отображения множества учеников в классе во множество всех фамилий.
. Классный журнал является примером отображения множества учеников в классе во множество всех фамилий.
Отображение 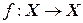 называется тождественным
называется тождественным


 (читается: отображение f множества X во множество Y), если задан закон, по которому каждому элементу
(читается: отображение f множества X во множество Y), если задан закон, по которому каждому элементу 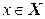 ставится в соответствие вполне определенный элемент
ставится в соответствие вполне определенный элемент 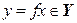 (рис. 4.1).
(рис. 4.1).
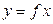 , то
, то 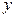 называется образом элемента
называется образом элемента 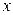 ;
;  Примерами отображений являются функции, которые изучаются в школьном курсе математики и в математическом анализе, например, функция
Примерами отображений являются функции, которые изучаются в школьном курсе математики и в математическом анализе, например, функция 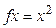 – отображение
– отображение 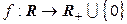 . Классный журнал является примером отображения множества учеников в классе во множество всех фамилий.
. Классный журнал является примером отображения множества учеников в классе во множество всех фамилий.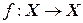 называется тождественным, если оно любой элемент оставляет на месте. Тождественное отображение множества X на себя будем обозначать
называется тождественным, если оно любой элемент оставляет на месте. Тождественное отображение множества X на себя будем обозначать 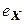 . Таким образом,
. Таким образом, 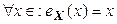 .
.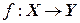 называется взаимно однозначным (или биективным, или биекцией), если оно удовлетворяет двум условиям:
называется взаимно однозначным (или биективным, или биекцией), если оно удовлетворяет двум условиям: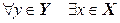 такой, что
такой, что 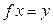 .
.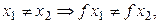
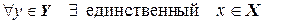 такой, что
такой, что 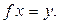
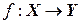 и
и 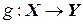 называются равными, если
называются равными, если 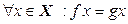 .
.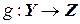 . Произведением (или композицией) отображений f и g называется отображение
. Произведением (или композицией) отображений f и g называется отображение 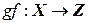 такое, что
такое, что 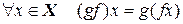 (рис. 4.2).
(рис. 4.2).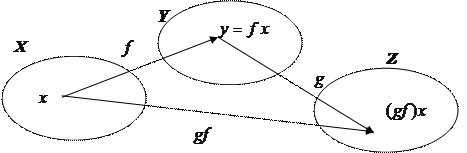
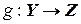 и
и 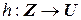 , то
, то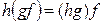 .
.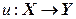 и
и 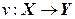 нужно показать, что
нужно показать, что 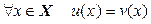 .
.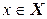 . Тогда
. Тогда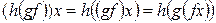 ; (4.1)
; (4.1)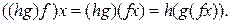 (4.2)
(4.2)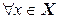 :
: 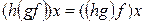 и поэтому,
и поэтому, 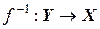 называется обратным к отображению
называется обратным к отображению 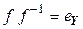 и
и 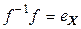 (рис. 4.3).
(рис. 4.3).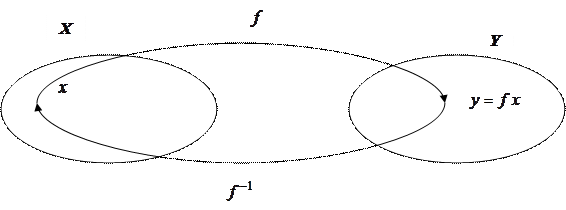
 и
и  – линейные пространства над одним и тем же полем
– линейные пространства над одним и тем же полем 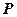 . Отображение
. Отображение 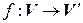 называется линейным оператором, если оно удовлетворяет следующим условиям:
называется линейным оператором, если оно удовлетворяет следующим условиям: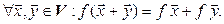
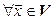
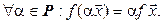
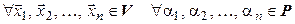 :
: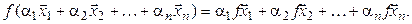 (4.3)
(4.3)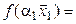 [2*]
[2*] 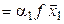 – истинно.
– истинно.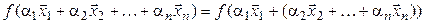 = [1*] =
= [1*] =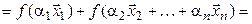 [2* и предположение индукции] =
[2* и предположение индукции] =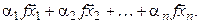 t
t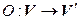 :
: 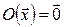 . Очевидно, этот оператор удовлетворяет условиям 1* и 2*, значит, является линейным.
. Очевидно, этот оператор удовлетворяет условиям 1* и 2*, значит, является линейным.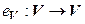 также, очевидно, является линейным.
также, очевидно, является линейным.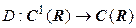 , который каждой дифференцируемой функции ставит в соответствие ее производную, является линейным, так как производная суммы функций равна сумме их производных, а при умножении функции на число ее производная умножается на это число.
, который каждой дифференцируемой функции ставит в соответствие ее производную, является линейным, так как производная суммы функций равна сумме их производных, а при умножении функции на число ее производная умножается на это число.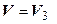 – пространство свободных векторов,
– пространство свободных векторов, 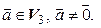
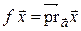 является линейным.
является линейным.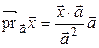 . Тогда
. Тогда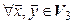 :
: 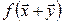 =
= 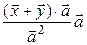 =
= 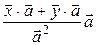 =
= 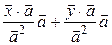 =
= 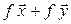 ;
;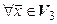
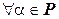 :
: 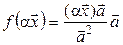 =
= 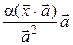 =
= 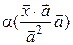 =
= 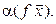
 5. В пространстве
5. В пространстве 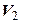 векторов плоскости, закрепленных в начале координат О, рассмотрим оператор
векторов плоскости, закрепленных в начале координат О, рассмотрим оператор 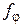 поворота вектора на угол
поворота вектора на угол 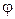 против часовой стрелки и докажем его линейность.
против часовой стрелки и докажем его линейность.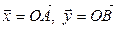 – произвольные векторы,
– произвольные векторы,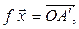
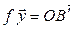 (рис. 4.4),
(рис. 4.4), 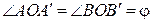 . Построим
. Построим 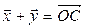 и
и 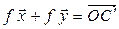 по правилу параллелограмма. Так как плоскость поворачивается
по правилу параллелограмма. Так как плоскость поворачивается Рис.4.4 как жесткое целое, методами элементарной геометрии нетрудно показать, что при этом повороте диагональ
Рис.4.4 как жесткое целое, методами элементарной геометрии нетрудно показать, что при этом повороте диагональ 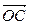 переходит в диагональ
переходит в диагональ 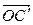 . Значит,
. Значит, 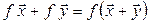 .
.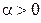 ,
, 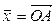 ,
, 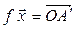 ,
, 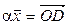 ,
, 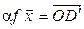 (рис.4.5). Очевидно, вектор
(рис.4.5). Очевидно, вектор 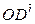 получен из
получен из 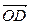 поворотом на угол
поворотом на угол 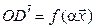 , а значит,
, а значит, 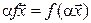 . Аналогично это свойство проверяется и при
. Аналогично это свойство проверяется и при 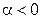 , а при
, а при 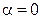 оно очевидно.◄
оно очевидно.◄
 и
и 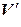 – линейные пространства над одним и тем же полем P и пусть в пространстве
– линейные пространства над одним и тем же полем P и пусть в пространстве 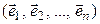 , (4.4)
, (4.4)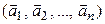 . (4.5)
. (4.5)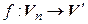 , переводящий базис (4.4) в систему (4.5), то есть такой, что
, переводящий базис (4.4) в систему (4.5), то есть такой, что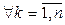 :
: 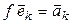 . (4.6)
. (4.6)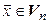 и разложим его по базису (4.4):
и разложим его по базису (4.4): 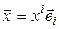 . Положим по определению
. Положим по определению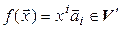 .
.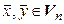 – произвольные векторы,
– произвольные векторы, 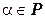 , то
, то 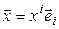 ,
, 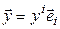 ,
, 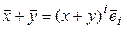
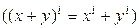 ,
, 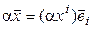 . Тогда
. Тогда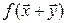 = [определение f ] =
= [определение f ] = 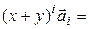
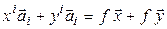 ;
;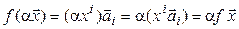 .
.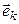 в базисе (4.3) равны нулю, за исключением k -й, которая равна 1. Таким образом, i -я координата вектора
в базисе (4.3) равны нулю, за исключением k -й, которая равна 1. Таким образом, i -я координата вектора 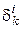 , то есть
, то есть 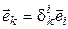 . Тогда
. Тогда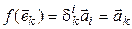 ,
,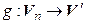 ,
, 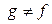 , переводящий (4.4) в (4.5), то есть такой, что
, переводящий (4.4) в (4.5), то есть такой, что 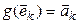 . Тогда
. Тогда 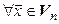 :
: 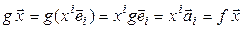 – противоречие.◄
– противоречие.◄ в любом базисе является нулевая матрица; матрицей тождественного оператора
в любом базисе является нулевая матрица; матрицей тождественного оператора  также в любом базисе является матрица единичная.
также в любом базисе является матрица единичная.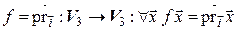 . Составим матрицу оператора проектирования на ось O x в базисе
. Составим матрицу оператора проектирования на ось O x в базисе 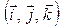 . Для этого находим образы базисных векторов и разлагаем их по базису:
. Для этого находим образы базисных векторов и разлагаем их по базису: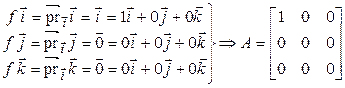 .
.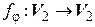 поворота плоскости на угол
поворота плоскости на угол 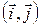 . Из рис. 4.5 и 4.6 видно, что
. Из рис. 4.5 и 4.6 видно, что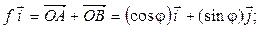
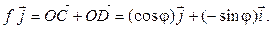
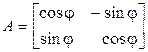 .
.

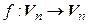 можно поставить в соответствие его матрицу в этом базисе, т. е. квадратную матрицу A n- го порядка, причем эта матрица определяется однозначно.
можно поставить в соответствие его матрицу в этом базисе, т. е. квадратную матрицу A n- го порядка, причем эта матрица определяется однозначно.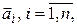 вектор, координатный столбец которого в базисе (4.8) совпадает с i -м столбцом матрицы А. Получим упорядоченную систему векторов
вектор, координатный столбец которого в базисе (4.8) совпадает с i -м столбцом матрицы А. Получим упорядоченную систему векторов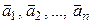 )
) 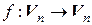 такой, что
такой, что 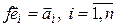 . По определению матрица этого оператора в базисе (4.8) совпадает с А.
. По определению матрица этого оператора в базисе (4.8) совпадает с А.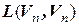 – множество всех линейных операторов линейного пространства
– множество всех линейных операторов линейного пространства 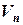 задан базис, то определяется отображение
задан базис, то определяется отображение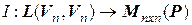 ,
,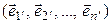 , (4.17)
, (4.17)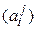 и
и 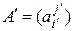 – матрицы линейного оператора
– матрицы линейного оператора 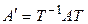 , (4.18)
, (4.18)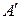 , следует образы векторов базиса (4.17) разложить опять же по этому базису. Имеем
, следует образы векторов базиса (4.17) разложить опять же по этому базису. Имеем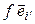 = [определение матрицы перехода] =
= [определение матрицы перехода] = 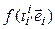 = [(4.3)] =
= [(4.3)] = 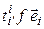 =
=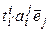 = [свойство 6º § 9 гл. 3] =
= [свойство 6º § 9 гл. 3] = 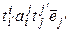 .
.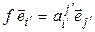 . (4.20)
. (4.20)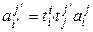 , (4.21)
, (4.21)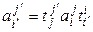 . (4.22)
. (4.22)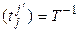 (см. замечание в § 9 гл. 3), то из (4.22) получаем (4.18).◄
(см. замечание в § 9 гл. 3), то из (4.22) получаем (4.18).◄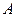 и
и  называются подобными, если существует невырожденная матрица Т такая, что
называются подобными, если существует невырожденная матрица Т такая, что 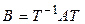 .
.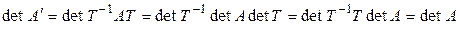 .
.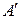 подобны и пусть подобие осуществляется при помощи матрицы
подобны и пусть подобие осуществляется при помощи матрицы 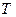 . Покажем, что матрица
. Покажем, что матрица 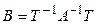 , подобная матрице
, подобная матрице 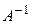 , является обратной к
, является обратной к 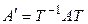 . Действительно,
. Действительно, 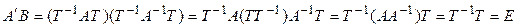 .◄
.◄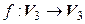 – линейный оператор,
– линейный оператор, 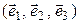 , и пусть
, и пусть 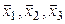 – некомпланарные векторы, а
– некомпланарные векторы, а 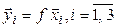 – их образы. Обозначим
– их образы. Обозначим 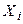 и
и 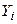 координатные столбцы в выбранном базисе векторов
координатные столбцы в выбранном базисе векторов 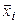 и
и 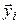 соответственно,
соответственно, 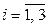 ,
, 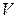 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах 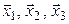 , а
, а 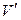 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах 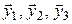 . Тогда, учитывая (4.15), получаем
. Тогда, учитывая (4.15), получаем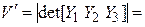 [(4.15) § 3]
[(4.15) § 3] 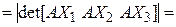 [§ 5 гл. 1] =
[§ 5 гл. 1] =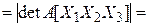 [§ 6 гл. 1]
[§ 6 гл. 1] 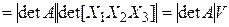 . (4.23)
. (4.23)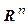 . Выберем в нем точку
. Выберем в нем точку 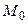 и
и 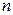 линейно независимых векторов
линейно независимых векторов 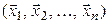 ,
, 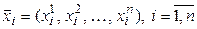 . Параллелепипедом в
. Параллелепипедом в 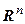 (
(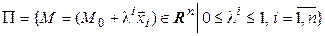 . (4.24)
. (4.24)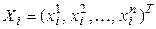 координатный столбец вектора
координатный столбец вектора 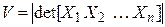 .
.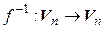 , который также является линейным. При этом, если А – матрица оператора
, который также является линейным. При этом, если А – матрица оператора 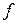 в некотором базисе, то матрица оператора
в некотором базисе, то матрица оператора 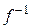 в том же базисе совпадает с матрицей
в том же базисе совпадает с матрицей 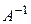 .
.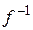 и
и 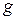 . Тогда
. Тогда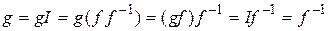
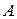 – матрица оператора
– матрица оператора 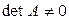 , значит, существует
, значит, существует 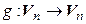 – тот линейный оператор, матрица которого в выбранном базисесовпадаетс
– тот линейный оператор, матрица которого в выбранном базисесовпадаетс 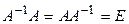 , и так как произведению матриц соответствует произведение операторов, то
, и так как произведению матриц соответствует произведение операторов, то 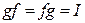 , и, таким образом,
, и, таким образом, 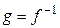 .◄
.◄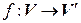 имеет единственный обратный, который тоже является линейным.
имеет единственный обратный, который тоже является линейным.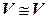 – рефлективность (изоморфизм осуществляет тождественное отображение).
– рефлективность (изоморфизм осуществляет тождественное отображение).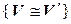

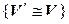 – симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью
– симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью 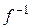 ).
).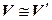 ,
, 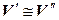 }
} 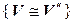 – транзитивность (если первый изоморфизм осуществляется с помощью отображения
– транзитивность (если первый изоморфизм осуществляется с помощью отображения 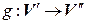 , то третий изоморфизм осуществляется с помощью отображения
, то третий изоморфизм осуществляется с помощью отображения 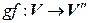 ).
).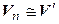 и пусть
и пусть 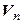 какой-либо базис
какой-либо базис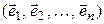 (4.27)
(4.27)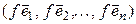 – (4.28)
– (4.28)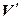 . Действительно, в силу взаимной однозначности f,
. Действительно, в силу взаимной однозначности f, 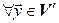
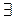 единственный
единственный 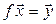 . Тогда, если
. Тогда, если 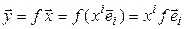 . Значит, (4.28) – система образующих в
. Значит, (4.28) – система образующих в 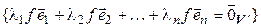
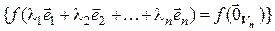
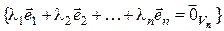
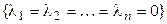
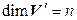 . ◄
. ◄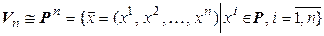 .
.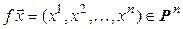 . Очевидно, отображение
. Очевидно, отображение 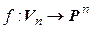 – взаимно однозначное. Кроме того,
– взаимно однозначное. Кроме того, 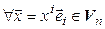 ,
, 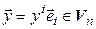 :
: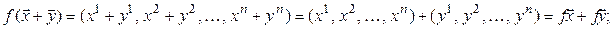
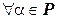
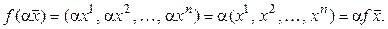
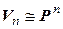 .
.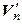 – n- мерные линейные пространства над одним и тем же полем Р. Тогда
– n- мерные линейные пространства над одним и тем же полем Р. Тогда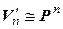 }
} 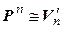 и }
и } 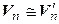 }.◄
}.◄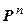 .
.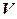 над полем
над полем 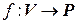 .
.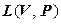 всех линейных форм на линейном пространстве
всех линейных форм на линейном пространстве 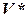 , его элементы назовем ковекторами и тоже для удобства отметим стрелками, но снизу (например,
, его элементы назовем ковекторами и тоже для удобства отметим стрелками, но снизу (например, 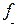 ).
).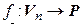 – линейная форма. Тогда
– линейная форма. Тогда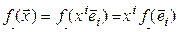 . (4.38)
. (4.38)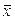 зависит от его координат и некоторых чисел
зависит от его координат и некоторых чисел 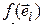 , вовсе с вектором
, вовсе с вектором 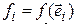 и назовем эти числа компонентами формы
и назовем эти числа компонентами формы 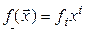 .
.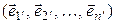 (4.39)
(4.39)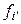 компоненты линейной формы
компоненты линейной формы 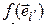 = [определение матрицы перехода] =
= [определение матрицы перехода] = 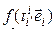 =
=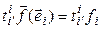 .
.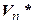 выберем
выберем 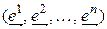 (4.40)
(4.40)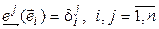 ,
,  принимает значение, равное 0, для всех базисных векторов, за исключением одного,
принимает значение, равное 0, для всех базисных векторов, за исключением одного, 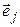 , для которого она принимает значение, равное 1. Существование таких форм вытекает из теоремы 4.1. Докажем линейную независимость (4.40). Как обычно, составим линейную комбинацию и приравняем ее нейтральному элементу.
, для которого она принимает значение, равное 1. Существование таких форм вытекает из теоремы 4.1. Докажем линейную независимость (4.40). Как обычно, составим линейную комбинацию и приравняем ее нейтральному элементу.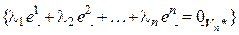
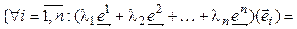
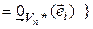
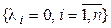
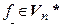 – произвольная линейная форма,
– произвольная линейная форма, 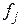 – ее компоненты в базисе (4.40). Обозначим
– ее компоненты в базисе (4.40). Обозначим 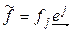 . Тогда
. Тогда