Пусть в линейном пространстве 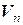 задан базис (4.8) и пусть
задан базис (4.8) и пусть 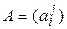 – матрица линейного оператора
– матрица линейного оператора 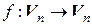 в этом базисе. Выберем произвольный вектор
в этом базисе. Выберем произвольный вектор 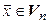 и положим
и положим 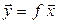 . Обозначим
. Обозначим 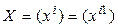 и
и 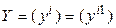 – координатные столбцы векторов
– координатные столбцы векторов 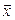 и
и 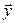 соответственно в базисе (4.8). Тогда
соответственно в базисе (4.8). Тогда
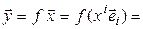 [(4.3)]
[(4.3)] 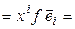 [(4.11)] =
[(4.11)] = 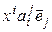 ,
,
и
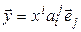 . (4.13)
. (4.13)
Равенство (4.13) есть не что иное, как разложение вектора 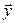 по базису (4.8), а коэффициенты разложения –координаты вектора
по базису (4.8), а коэффициенты разложения –координаты вектора 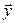 в этом базисе. В силу единственности координат вектора в данном базисе получаем
в этом базисе. В силу единственности координат вектора в данном базисе получаем
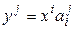 . (4.14)
. (4.14)
Записав (4.14) по правилу цепочки (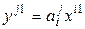 ), получаем
), получаем
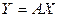 . (4.15)
. (4.15)
Формула (4.14) и задает связь координат вектора и координат его образа при линейном операторе, а (4.15) –ее матричная запись.
Изменение матрицы линейного оператора
При изменении базиса
Теорема 4.2. Пусть в линейном пространстве 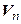 заданы два базиса:
заданы два базиса:
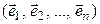 (4.16)
(4.16)
и
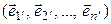 , (4.17)
, (4.17)
и пусть A = 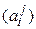 и
и 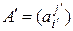 – матрицы линейного оператора
– матрицы линейного оператора 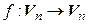 в базисах (4.16) и (4.17) соответственно. Тогда
в базисах (4.16) и (4.17) соответственно. Тогда
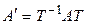 , (4.18)
, (4.18)
где Т – матрица перехода от (4.16) к (4.17).
►Чтобы найти матрицу 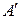 , следует образы векторов базиса (4.17) разложить опять же по этому базису. Имеем
, следует образы векторов базиса (4.17) разложить опять же по этому базису. Имеем
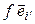 = [определение матрицы перехода] =
= [определение матрицы перехода] = 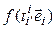 = [(4.3)] =
= [(4.3)] = 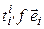 =
=
= [(4.11)] = 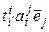 = [свойство 6º § 9 гл. 3] =
= [свойство 6º § 9 гл. 3] = 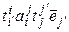 .
.
Итак,
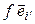 =
= 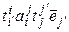 . (4.19)
. (4.19)
Равенство (4.19) задает разложение вектора 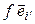 по базису (4.17). С другой стороны, по определению матрицы линейного оператора,
по базису (4.17). С другой стороны, по определению матрицы линейного оператора,
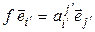 . (4.20)
. (4.20)
В силу единственности координат вектора в данном базисе из (4.19) и (4.20) получаем равенство
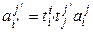 , (4.21)
, (4.21)
которое и дает нам связь элементов матриц линейного оператора в различных базисах. Запишем (4.21) по правилу цепочки:
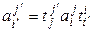 . (4.22)
. (4.22)
Так как 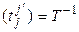 (см. замечание в § 9 гл. 3), то из (4.22) получаем (4.18).◄
(см. замечание в § 9 гл. 3), то из (4.22) получаем (4.18).◄
Определение. Квадратные матрицы 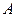 и
и 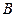 называются подобными, если существует невырожденная матрица Т такая, что
называются подобными, если существует невырожденная матрица Т такая, что 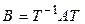 .
.
Таким образом, мы видим, что матрицы линейного оператора в различных базисах подобны.
Лемма 4.1. 1. Подобные матрицы имеют одинаковые определители.
2. Если невырожденные квадратные матрицы подобны, то обратные к ним тоже подобны, причем подобие осуществляется при помощи одной и той же матрицы,
►1. 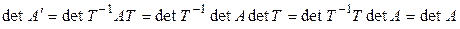 .
.
2. Пусть матрицы  и
и  подобны и пусть подобие осуществляется при помощи матрицы
подобны и пусть подобие осуществляется при помощи матрицы 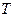 . Покажем, что матрица
. Покажем, что матрица 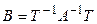 , подобная матрице
, подобная матрице 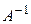 , является обратной к
, является обратной к 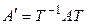 . Действительно,
. Действительно, 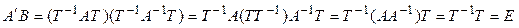 .◄
.◄
Определение. Определителем линейного оператора 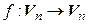 называется определитель его матрицы в некотором, а значит, и в любом базисе пространства
называется определитель его матрицы в некотором, а значит, и в любом базисе пространства 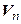 .
.
Геометрический смысл определителя
Линейного оператора
Пусть 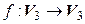 – линейный оператор,
– линейный оператор, 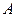 – его матрица в некотором ортонормированном базисе
– его матрица в некотором ортонормированном базисе 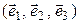 , и пусть
, и пусть 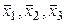 – некомпланарные векторы, а
– некомпланарные векторы, а 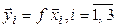 – их образы. Обозначим
– их образы. Обозначим 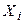 и
и 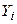 координатные столбцы в выбранном базисе векторов
координатные столбцы в выбранном базисе векторов 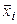 и
и 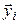 соответственно,
соответственно, 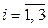 ,
, 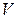 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах 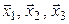 , а
, а 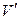 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах 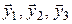 . Тогда, учитывая (4.15), получаем
. Тогда, учитывая (4.15), получаем
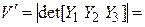 [(4.15) § 3]
[(4.15) § 3] 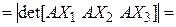 [§ 5 гл. 1] =
[§ 5 гл. 1] =
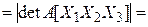 [§ 6 гл. 1]
[§ 6 гл. 1] 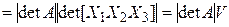 . (4.23)
. (4.23)
Рассмотрим теперь пространство 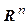 . Выберем в нем точку
. Выберем в нем точку 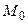 и
и 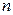 линейно независимых векторов
линейно независимых векторов 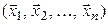 ,
, 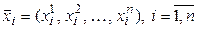 . Параллелепипедом в
. Параллелепипедом в 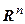 (
(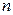 -мерным параллелепипедом) будем называть множество точек в
-мерным параллелепипедом) будем называть множество точек в 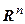
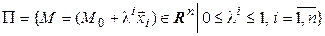 . (4.24)
. (4.24)
Обозначим 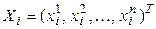 координатный столбец вектора
координатный столбец вектора 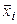 в каноническом базисе. По аналогии с трехмерным пространством, объемом
в каноническом базисе. По аналогии с трехмерным пространством, объемом 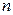 -мерного параллелепипеда (4.24) будем называть число
-мерного параллелепипеда (4.24) будем называть число
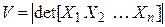 .
.
Можно доказать, что при переходе от одного ортонормированного базиса к другому ортонормированному это число не меняется, т.е. определение объема параллелепипеда является корректным.
Так же, как и для трехмерного пространства, для пространства 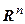 доказывается равенство (4.23).
доказывается равенство (4.23).
Вывод: из формулы (4.23) на основании леммы 4.1 вытекает, что коэффициент изменения объема параллелепипеда при линейном операторе равен модулю определителя этого оператора.



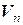 задан базис (4.8) и пусть
задан базис (4.8) и пусть 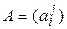 – матрица линейного оператора
– матрица линейного оператора 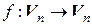 в этом базисе. Выберем произвольный вектор
в этом базисе. Выберем произвольный вектор 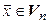 и положим
и положим 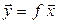 . Обозначим
. Обозначим 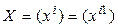 и
и 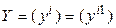 – координатные столбцы векторов
– координатные столбцы векторов 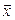 и
и 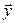 соответственно в базисе (4.8). Тогда
соответственно в базисе (4.8). Тогда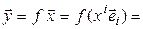 [(4.3)]
[(4.3)] 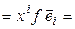 [(4.11)] =
[(4.11)] = 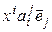 ,
,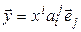 . (4.13)
. (4.13)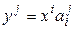 . (4.14)
. (4.14)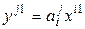 ), получаем
), получаем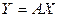 . (4.15)
. (4.15)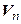 заданы два базиса:
заданы два базиса: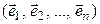 (4.16)
(4.16)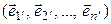 , (4.17)
, (4.17)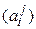 и
и 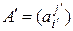 – матрицы линейного оператора
– матрицы линейного оператора 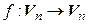 в базисах (4.16) и (4.17) соответственно. Тогда
в базисах (4.16) и (4.17) соответственно. Тогда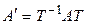 , (4.18)
, (4.18)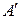 , следует образы векторов базиса (4.17) разложить опять же по этому базису. Имеем
, следует образы векторов базиса (4.17) разложить опять же по этому базису. Имеем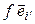 = [определение матрицы перехода] =
= [определение матрицы перехода] = 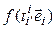 = [(4.3)] =
= [(4.3)] = 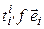 =
=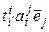 = [свойство 6º § 9 гл. 3] =
= [свойство 6º § 9 гл. 3] = 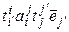 .
.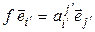 . (4.20)
. (4.20)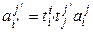 , (4.21)
, (4.21)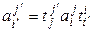 . (4.22)
. (4.22)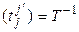 (см. замечание в § 9 гл. 3), то из (4.22) получаем (4.18).◄
(см. замечание в § 9 гл. 3), то из (4.22) получаем (4.18).◄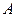 и
и 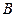 называются подобными, если существует невырожденная матрица Т такая, что
называются подобными, если существует невырожденная матрица Т такая, что 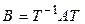 .
.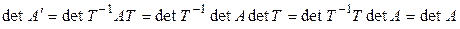 .
.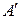 подобны и пусть подобие осуществляется при помощи матрицы
подобны и пусть подобие осуществляется при помощи матрицы 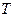 . Покажем, что матрица
. Покажем, что матрица 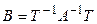 , подобная матрице
, подобная матрице 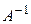 , является обратной к
, является обратной к 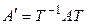 . Действительно,
. Действительно, 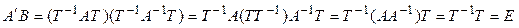 .◄
.◄ – линейный оператор,
– линейный оператор,  , и пусть
, и пусть 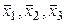 – некомпланарные векторы, а
– некомпланарные векторы, а 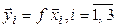 – их образы. Обозначим
– их образы. Обозначим 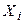 и
и 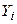 координатные столбцы в выбранном базисе векторов
координатные столбцы в выбранном базисе векторов 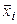 и
и 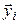 соответственно,
соответственно, 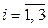 ,
, 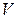 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах 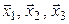 , а
, а 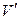 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах 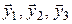 . Тогда, учитывая (4.15), получаем
. Тогда, учитывая (4.15), получаем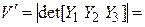 [(4.15) § 3]
[(4.15) § 3] 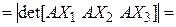 [§ 5 гл. 1] =
[§ 5 гл. 1] =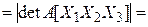 [§ 6 гл. 1]
[§ 6 гл. 1] 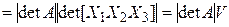 . (4.23)
. (4.23)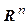 . Выберем в нем точку
. Выберем в нем точку 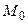 и
и 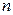 линейно независимых векторов
линейно независимых векторов 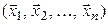 ,
, 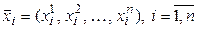 . Параллелепипедом в
. Параллелепипедом в 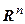 (
(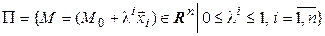 . (4.24)
. (4.24)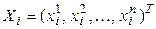 координатный столбец вектора
координатный столбец вектора 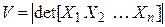 .
.


