

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Интересное:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Определение 9.1. Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.
Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс, при пересечении образующих обеих полостей – гипербола, а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола.
Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух переменных:
 .
.
Эллипс.
Определение 9.2. Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами, есть величина постоянная.
Замечание. При совпадении точек F 1 и F 2 эллипс превращается в окружность.
Выведем уравнение эллипса, выбрав декартову систему


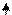

 у М(х,у) координат так, чтобы ось Ох совпала с прямой F 1 F 2, начало
у М(х,у) координат так, чтобы ось Ох совпала с прямой F 1 F 2, начало
r1 r2 координат – с серединой отрезка F 1 F 2. Пусть длина этого
отрезка равна 2 с, тогда в выбранной системе координат
F1 O F2 x F 1(- c, 0), F 2(c, 0). Пусть точка М(х, у) лежит на эллипсе, и
сумма расстояний от нее до F 1 и F 2 равна 2 а.
Тогда r 1 + r 2 = 2 a, но 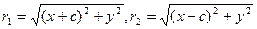 ,
,
поэтому 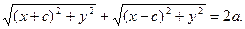 Введя обозначение b ² = a ²- c ² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса:
Введя обозначение b ² = a ²- c ² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса:  (9.1)
(9.1)
|
|
Определение 9.3. Эксцентриситетом эллипса называется величина е=с/а (9.2)
Определение 9.4. Директрисой Di эллипса, отвечающей фокусу Fi, называется прямая, расположенная в одной полуплоскости с Fi относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.
Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (9.1), а уравнением второй степени другого вида.
Свойства эллипса:
1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2 а и 2 b (2 a >2 b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.
2) Весь эллипс содержится внутри прямоугольника 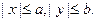
3) Эксцентриситет эллипса e < 1.
Действительно, 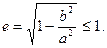
4) Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно а/е, а е <1, следовательно, а/е> a, а весь эллипс лежит в прямоугольнике 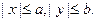 )
)
5) Отношение расстояния ri от точки эллипса до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.
Доказательство.
Расстояния от точки М(х, у) до фокусов эллипса можно представить так:
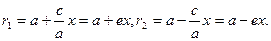 Составим уравнения директрис:
Составим уравнения директрис:
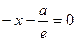 (D 1),
(D 1), 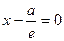 (D 2). Тогда
(D 2). Тогда  Отсюда ri / di = e, что и требовалось доказать.
Отсюда ri / di = e, что и требовалось доказать.
Гипербола.
Определение 9.5. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами, есть величина постоянная.
Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями.
|
|
| r1 - r2| = 2 a, откуда 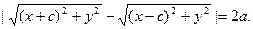 Если обозначить b ² = c ² - a ², отсюда можно получить
Если обозначить b ² = c ² - a ², отсюда можно получить
 - каноническое уравнение гиперболы. (9.3)
- каноническое уравнение гиперболы. (9.3)
Определение 9.6. Эксцентриситетом гиперболы называется величина е = с / а.
Определение 9.7. Директрисой Di гиперболы, отвечающей фокусу Fi, называется прямая, расположенная в одной полуплоскости с Fi относительно оси Оу перпендикулярно оси Ох на расстоянии а / е от начала координат.
Свойства гиперболы:
1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.
2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями
 и
и  .
.
3) Наряду с гиперболой (9.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением
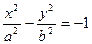 , (9.3`)
, (9.3`)
для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.
4) Эксцентриситет гиперболы e > 1.
5) Отношение расстояния ri от точки гиперболы до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.
Доказательство можно провести так же, как и для эллипса.
Парабола.
Определение 9.8. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой.

 у Для вывода уравнения параболы выберем декартову
у Для вывода уравнения параболы выберем декартову
систему координат так, чтобы ее началом была середина


 d M(x,y) перпендикуляра FD, опущенного из фокуса на директри-
d M(x,y) перпендикуляра FD, опущенного из фокуса на директри-
|
|
r су, а координатные оси располагались параллельно и
перпендикулярно директрисе. Пусть длина отрезка FD
D O F x равна р. Тогда из равенства r = d следует, что
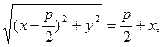 поскольку
поскольку
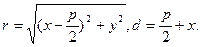 Алгебраическими преобразованиями это уравнение можно привести к виду: y ² = 2 px, (9.4)
Алгебраическими преобразованиями это уравнение можно привести к виду: y ² = 2 px, (9.4)
называемому каноническим уравнением параболы. Величина р называется параметром параболы.
Свойства параболы:
1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.
2) Вся парабола расположена в правой полуплоскости плоскости Оху.
Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:
Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e <1), гиперболу (при e >1) или параболу (при е =1).
Лекция 10.
Поверхности второго порядка. Канонические уравнения основных поверхностей второго порядка: эллипсоидов, гиперболоидов и параболоидов.
Поверхности второго порядка.
Определение 10.1. Поверхностью второго порядка называется множество точек трехмерного пространства, декартовы координаты которых удовлетворяют уравнению вида:
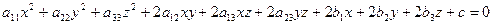 - (10.1)
- (10.1)
уравнению второй степени от трех неизвестных, называемому общим уравнением поверхности второго порядка.
Эллипсоид.
Определение 10.2. Эллипсоидом называется поверхность, которая в некоторой системе прямоугольных декартовых координат определяется уравнением
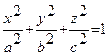 . (10.2)
. (10.2)
Уравнение (10.2) называется каноническим уравнением эллипсоида. Величины a, b, c - полуоси эллипсоида. Сечением эллипсоида любой плоскостью, параллельной координатным плоскостям, является эллипс (в частном случае окружность).
|
|
Координаты точек эллипсоида удовлетворяют неравенствам - a £ x £ a, - b £ y £ b, - c £ z £ c.
В частном случае, при a= b, эллипсоид является поверхностью вращения, получающейся при вращении вокруг оси Oz эллипса 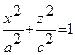 , лежащего в плоскости xOz. При a = b = с эллипсоид представляет собой сферу.
, лежащего в плоскости xOz. При a = b = с эллипсоид представляет собой сферу.
Гиперболоиды.
Определение 10.3. Гиперболоидами называются поверхности, которые в некоторой системе прямоугольных декартовых координат определяются каноническими уравнениями
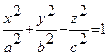 , (10.3)
, (10.3)
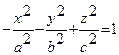 . (10.4)
. (10.4)
Гиперболоид, определяемый уравнением (10.3), называется однополостным; гиперболоид, определяемый уравнением (10.4), называется двуполостным. Для обоих видов гиперболоидов сечения, параллельные оси Oz - гиперболы (для однополостного гиперболоида в сечении может быть пара пересекающихся прямых); сечения, параллельные плоскости xOy - эллипсы.
Величины a, b, с называются полуосями гиперболоида.
Замечание. При a= b гиперболоиды являются поверхностями вращения.
Параболоиды.
Определение 10.4. Параболоидами называются поверхности, которые в некоторой системе прямоугольных декартовых координат определяются каноническими уравнениями
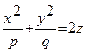 , (10.5)
, (10.5)
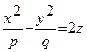 , (10.6)
, (10.6)
где p и q - положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (10.5), называется эллиптическим. Сечения эллиптического параболоида, параллельные оси Oz - параболы; сечения, параллельные плоскости xOy - эллипсы. Параболоид, определяемый уравнением (10.6), называется гиперболическим. Сечения гиперболического параболоида, параллельные плоскостям yOz и xOz - параболы; сечения, параллельные плоскости xOy - гиперболы.
Замечание. В случае, когда p = q, эллиптический параболоид (10.5) является поверхностью вращения (вокруг оси Oz).
Пример. Определить вид поверхности
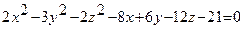 ,
,
используя метод сечения плоскостями.
Решение. Уравнение поверхности не содержит членов с произведением координат, следовательно плоскости симметрий параллельны координатным плоскостям.
Пересекая поверхность плоскостями 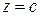 параллельными плоскости xOy, получим:
параллельными плоскости xOy, получим:
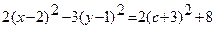 .
.
Так как 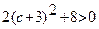 для любого с, полученная кривая является гиперболой с действительной осью, параллельной оси Ox.
для любого с, полученная кривая является гиперболой с действительной осью, параллельной оси Ox.
Пересекая поверхность плоскостями  аналогично получаем уравнение
аналогично получаем уравнение
|
|

гиперболы с действительной осью, параллельной оси Ox.
При пересечении данной поверхности плоскостями  , параллельными координатной плоскости yOz, получаем:
, параллельными координатной плоскости yOz, получаем:
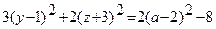 .
.
Последнее уравнение при  ,т.е. при
,т.е. при  и
и 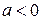 , есть уравнение эллипса.
, есть уравнение эллипса.
Таким образом сечениями поверхности плоскостями являются эллипсы и гиперболы, действительные оси которых параллельны. Следовательно, исследуемая поверхность - двуполостный гиперболоид. Его уравнение можно преобразовать к каноническому виду:
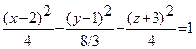 .
.
|
|
|

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!