Лекция 1.
Определение матрицы. Определители второго и третьего порядков, их основные свойства. Миноры и алгебраические дополнения, разложение определителя по строке (столбцу). Методы вычисления определителей. Понятие об определителе n-го порядка.
Определение 1.1. Матрицей называется прямоугольная таблица чисел.

Обозначения: А – матрица,  - элемент матрицы,
- элемент матрицы,  номер строки, в которой стоит данный элемент,
номер строки, в которой стоит данный элемент, 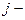 номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
Определение 1.2. Числа m и n называются размерностями матрицы.
Определение 1.3. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.
Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.

Определение 1.4. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
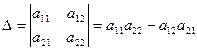 .
.
При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.
Примеры.
1.  2.
2. 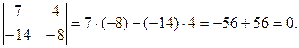
Определение 1.5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
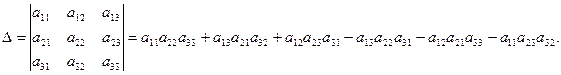
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:















 образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:
образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: 
 Примеры.
Примеры.
1. 
2. 
Определение1. 6. Транспонированием матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате получается матрица А`, называемая транспонированной по отношению к матрице А, элементы которой связаны с элементами А соотношением a` ij = aji.
Основные свойства определителей.
Сформулируем и докажем основные свойства определителей 2-го и 3-го порядка (доказательство проведем для определителей 3-го порядка).
Свойство 1. Определитель не изменяется при транспонировании, т.е.

Доказательство.

= 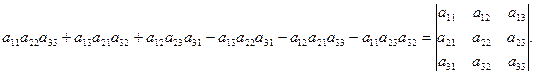
Замечание. Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.
Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.

 .
.
Доказательство.




Свойство 3. Определитель, имеющий нулевую строку, равен 0.
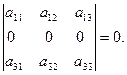
Доказательство этого свойства следует из свойства 2 при k = 0.
Свойство 4. Определитель, имеющий две равные строки, равен 0.

Доказательство.
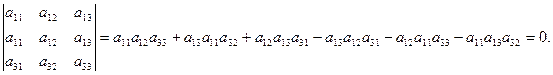
Свойство 5. Определитель, две строки которого пропорциональны, равен 0.
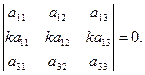
Доказательство следует из свойств 2 и 4.
Свойство 6. При перестановке двух строк определителя он умножается на –1.
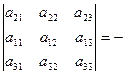

Доказательство.

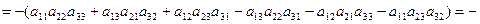

Свойство 7.
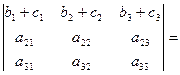
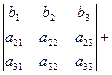

Доказательство этого свойства можно провести самостоятельно, сравнив значения левой и правой частей равенства, найденные с помощью определения 1.5.
Свойство 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.
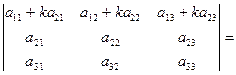

Доказательство следует из свойств 7 и 5.
Разложение определителя по строке.
Определение1. 7. Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент.
Обозначение:  выбранный элемент определителя,
выбранный элемент определителя, 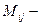 его минор.
его минор.
Пример. Для 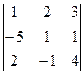
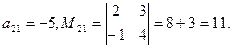
Определение1. 8. Алгебраическим дополнением  элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е.
элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е. 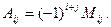
Рассмотрим еще один способ вычисления определителей третьего порядка – так называемое разложение по строке или столбцу. Для этого докажем следующую теорему:
Теорема 1.1. Определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения, т.е.
 где i=1,2,3.
где i=1,2,3.
Доказательство.
Докажем теорему для первой строки определителя, так как для любой другой строки или столбца можно провести аналогичные рассуждения и получить тот же результат.
Найдем алгебраические дополнения к элементам первой строки:

Тогда 
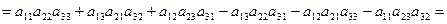

Таким образом, для вычисления определителя достаточно найти алгебраические дополнения к элементам какой-либо строки или столбца и вычислить сумму их произведений на соответствующие элементы определителя.
Пример. Вычислим определитель  с помощью разложения по первому столбцу. Заметим, что
с помощью разложения по первому столбцу. Заметим, что 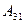 при этом искать не требуется, так как
при этом искать не требуется, так как 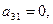 следовательно, и
следовательно, и  Найдем
Найдем 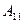 и
и 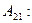
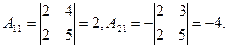 Следовательно,
Следовательно,
 =
= 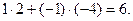
Определители более высоких порядков.
Определение1. 9. Определитель n-го порядка

есть сумма n! членов 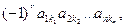 каждый из которых соответствует одному из n! упорядоченных множеств
каждый из которых соответствует одному из n! упорядоченных множеств  полученных r попарными перестановками элементов из множества 1,2,…,n.
полученных r попарными перестановками элементов из множества 1,2,…,n.
Замечание 1. Свойства определителей 3-го порядка справедливы и для определителей n-го порядка.
Замечание 2. На практике определители высоких порядков вычисляют с помощью разложения по строке или столбцу. Это позволяет понизить порядок вычисляемых определителей и в конечном счете свести задачу к нахождению определителей 3-го порядка.
Пример. Вычислим определитель 4-го порядка 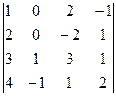 с помощью разложения по 2-му столбцу. Для этого найдем
с помощью разложения по 2-му столбцу. Для этого найдем  и
и 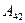 :
:
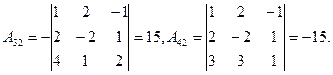 Следовательно,
Следовательно,
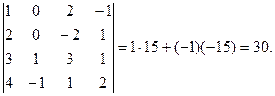
Лекция 2. Системы линейных уравнений. Метод Гаусса. Правило Крамера.
Определение 2.1. Линейными операциями над какими-либо объектами называются их сложение и умножение на число.
Определение 2.2. Линейной комбинацией переменных называется результат применения к ним линейных операций, т.е.  где
где  числа,
числа,  переменные.
переменные.
Определение 2.3. Линейным уравнением называется уравнение вида
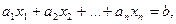 (2.1)
(2.1)
где 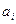 и b – числа,
и b – числа,  - неизвестные.
- неизвестные.
Таким образом, в левой части линейного уравнения стоит линейная комбинация неизвестных, а в правой – число.
Определение 2.4. Линейное уравнение называется однородным, если b = 0. В противном случае уравнение называется неоднородным.
Определение 2.5. Системой линейных уравнений (линейной системой) называется система вида
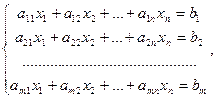 (2.2)
(2.2)
где  ,
,  - числа,
- числа,  - неизвестные, n – число неизвестных, m – число уравнений.
- неизвестные, n – число неизвестных, m – число уравнений.
Определение 2.6. Решением линейной системы (2.2) называется набор чисел
 которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.
которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.
Метод Гаусса решения линейных систем.
Замечание. Линейная система (2.2) может иметь единственное решение, бесконечно много решений или не иметь ни одного решения.
Примеры:
1. 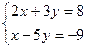 . Единственным решением является пара чисел х = 1, у = 2.
. Единственным решением является пара чисел х = 1, у = 2.
2.  . Решением этой системы будут любые два числа х и у, удовлетворяющие условию у = 3 – х. Например, х=1, у=2; х=0, у=3 и т. д.
. Решением этой системы будут любые два числа х и у, удовлетворяющие условию у = 3 – х. Например, х=1, у=2; х=0, у=3 и т. д.
3. 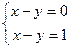 . Очевидно, что эта система не имеет решений, так как разность двух чисел не может принимать двух различных значений.
. Очевидно, что эта система не имеет решений, так как разность двух чисел не может принимать двух различных значений.
Условия существования и количества решений линейной системы будут изучены в дальнейшем, а пока рассмотрим способы нахождения единственного решения системы,
в которой число уравнений равно числу неизвестных: 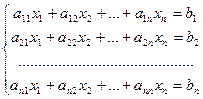 (2.3)
(2.3)
Пусть 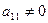 (этого всегда можно добиться, поменяв уравнения местами). Разделим обе части первого уравнения на
(этого всегда можно добиться, поменяв уравнения местами). Разделим обе части первого уравнения на 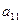 и вычтем полученное уравнение из каждого из остальных уравнений системы, умножив его предварительно на
и вычтем полученное уравнение из каждого из остальных уравнений системы, умножив его предварительно на 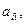 где i – номер очередного уравнения. Как известно, полученная при этом новая система будет равносильна исходной. Коэффициенты при
где i – номер очередного уравнения. Как известно, полученная при этом новая система будет равносильна исходной. Коэффициенты при  во всех уравнениях этой системы, начиная со второго, будут равны 0, т.е. система выглядит так:
во всех уравнениях этой системы, начиная со второго, будут равны 0, т.е. система выглядит так:
 .
.
Если новые коэффициенты при х2 не все равны нулю, можнотаким же образом исключить  из третьего и последующих уравнений. Продолжая эту операцию для следующих неизвестных, приведем систему к так называемому треугольному виду:
из третьего и последующих уравнений. Продолжая эту операцию для следующих неизвестных, приведем систему к так называемому треугольному виду:
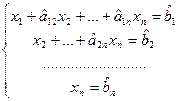 . (2.4)
. (2.4)
Здесь символами  и
и 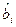 обозначены изменившиеся в результате преобразований числовые коэффициенты и свободные члены.
обозначены изменившиеся в результате преобразований числовые коэффициенты и свободные члены.
Из последнего уравнения системы (2.4) единственным образом определяется  , а затем последовательной подстановкой – остальные неизвестные.
, а затем последовательной подстановкой – остальные неизвестные.
Замечание. Иногда в результате преобразований в каком-либо из уравнений обращаются в 0 все коэффициенты и правая часть, то есть оно превращается в тождество 0=0. Исключив его из системы, мы уменьшим число уравнений по сравнению с числом неизвестных. Такая система не может иметь единственного решения.
Если же в процессе применения метода Гаусса какое-нибудь уравнение превратится в равенство вида 0=1 (коэффициенты при неизвестных обратились в 0, а правая часть приняла ненулевое значение), то исходная система не имеет решения, так как подобное равенство является неверным при любых значениях неизвестных.
Примеры:
1. Решим методом Гаусса систему 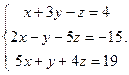
Вычтем из второго уравнения удвоенное первое, а из третьего – первое, умноженное на 5.
Получим: 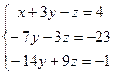 . Теперь вычтем из третьего уравнения удвоенное второе, а затем разделим второе уравнение на –7 (коэффициент при у), а третье – на 15 (новый коэффициент при z). Система примет вид:
. Теперь вычтем из третьего уравнения удвоенное второе, а затем разделим второе уравнение на –7 (коэффициент при у), а третье – на 15 (новый коэффициент при z). Система примет вид:
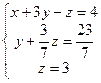 . Отсюда z=3, y=2, x=1 – единственное решение системы.
. Отсюда z=3, y=2, x=1 – единственное решение системы.
2. Система  после исключения х из второго и третьего уравнений примет вид:
после исключения х из второго и третьего уравнений примет вид: 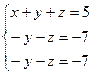 . Если затем вычесть второе уравнение из третьего, то последнее уравнение станет тождеством 0=0. В системе осталось два уравнения:
. Если затем вычесть второе уравнение из третьего, то последнее уравнение станет тождеством 0=0. В системе осталось два уравнения:  . Ее решение можно записать в виде: х = -2, у – любое число, z = 7 – y. Таким образом, система имеет бесконечно много решений.
. Ее решение можно записать в виде: х = -2, у – любое число, z = 7 – y. Таким образом, система имеет бесконечно много решений.
3.  . Применив к этой системе метод Гаусса, получим
. Применив к этой системе метод Гаусса, получим 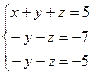 ,
,
откуда 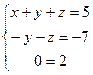 . Последнее равенство является неверным при любых значениях неизвестных, следовательно, система не имеет решения.
. Последнее равенство является неверным при любых значениях неизвестных, следовательно, система не имеет решения.
Правило Крамера.
Рассмотрим систему (2.3). Назовем главным определителем этой системы определитель  , элементами которого являются коэффициенты при неизвестных:
, элементами которого являются коэффициенты при неизвестных:

 .
.
Предположим сначала, что  Умножим каждое уравнение системы (2.3) на алгебраические дополнения
Умножим каждое уравнение системы (2.3) на алгебраические дополнения 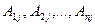 элементов j-го столбца
элементов j-го столбца 
Сложив затем все уравнения, получим:
 . (2.5)
. (2.5)
Отметим, что  .
.
(j-й столбец)
(Результат получен из разложения определителя по j-му столбцу). Такой определитель равен 0 при  и равен
и равен  при i = j. Правая часть равенства (2.5) представляет собой определитель
при i = j. Правая часть равенства (2.5) представляет собой определитель  , в котором вместо j-го столбца стоит столбец свободных членов системы (2.3). Назовем такой определитель
, в котором вместо j-го столбца стоит столбец свободных членов системы (2.3). Назовем такой определитель 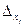 . Рассматривая j = 1,2 ,…, n, получим систему, эквивалентную исходной:
. Рассматривая j = 1,2 ,…, n, получим систему, эквивалентную исходной: 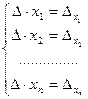 (2.6). Разделив все уравнения на
(2.6). Разделив все уравнения на  , найдем единственное решение:
, найдем единственное решение: 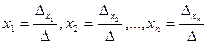 .
.
Предположим теперь, что  =0. Тогда система (2.6) примет вид:
=0. Тогда система (2.6) примет вид:  .
.
В этом случае, если все 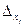 =0, система выглядит так:
=0, система выглядит так: 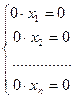 и имеет бесконечно много решений. Если же хотя бы один из
и имеет бесконечно много решений. Если же хотя бы один из 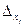
 система решений не имеет.
система решений не имеет.
Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:
1) Если 
 система (2.3) имеет единственное решение, определяемое по формулам:
система (2.3) имеет единственное решение, определяемое по формулам: 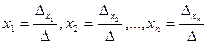 .
.
2) Если  =
= 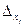 =0, система имеет бесконечно много решений.
=0, система имеет бесконечно много решений.
3) Если  =0, а хотя бы один из
=0, а хотя бы один из 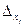
 система не имеет решений.
система не имеет решений.
Примеры:
- Рассмотрим систему
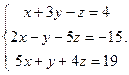 , решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:
, решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:
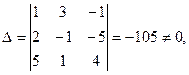 следовательно, система имеет единственное решение.
следовательно, система имеет единственное решение.
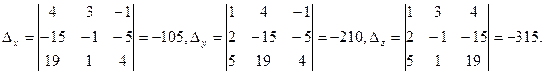
Отсюда 
2.  . Здесь
. Здесь 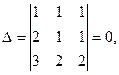 поскольку имеет два одинаковых столбца.
поскольку имеет два одинаковых столбца.
Следовательно, система не имеет единственного решения. Найдем  и
и 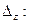
 поэтому система имеет бесконечно много решений.
поэтому система имеет бесконечно много решений.
3.  . Для этой системы
. Для этой системы 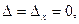 но
но 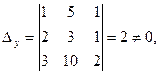
следовательно, решений нет.
Лекция 3.
Лекция 4.
Ранг матрицы. Теорема о ранге. Вычисление ранга матрицы. Совместность систем линейных уравнений. Теорема Кронекера-Капелли. Структура общего решения однородной системы линейных уравнений. Общее решение неоднородной системы линейных уравнений.
Определение 4.1. Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы.
Замечание. Таким образом, каждый элемент матрицы является ее минором 1-го порядка.
Определение 4.2. Ранг матрицы – это порядок ее наибольшего ненулевого минора.
Обозначения: r(A), R(A), Rang A.
Замечание. Очевидно, что значение ранга матрицы не может превышать меньшей из ее размерностей.
Примеры:
1. 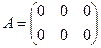 , r(A)=0.
, r(A)=0.
2. 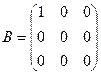 . Матрица В содержит единственный ненулевой элемент -
. Матрица В содержит единственный ненулевой элемент - 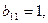 являющийся минором 1-го порядка. Все определители более высоких порядков, составленные из элементов этой матрицы, будут содержать 0-ю строку и поэтому равны 0. Следовательно, r(B)=1.
являющийся минором 1-го порядка. Все определители более высоких порядков, составленные из элементов этой матрицы, будут содержать 0-ю строку и поэтому равны 0. Следовательно, r(B)=1.
3. 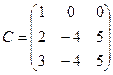 . Единственным минором 3-го порядка является определитель матрицы С, но он равен 0, поскольку содержит пропорциональные столбцы. Следовательно, r(C)<3.
. Единственным минором 3-го порядка является определитель матрицы С, но он равен 0, поскольку содержит пропорциональные столбцы. Следовательно, r(C)<3.
Для того, чтобы доказать, что r(C)=2, достаточно указать хотя бы один минор 2-го порядка, не равный 0, например, 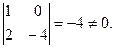 Значит, r(C)=2.
Значит, r(C)=2.
4. 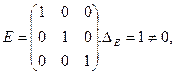 следовательно, r(E)=3.
следовательно, r(E)=3.
Замечание. Для матриц большой размерности непосредственное вычисление всех миноров затруднительно. Поэтому в этом случае можно преобразовать матрицу к так называемому треугольному виду (когда элементы, стоящие ниже 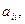 равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся:
равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся:
1) транспонирование
2) умножение строки на ненулевое число
3) перестановка строк
4) прибавление к элементам данной строки элементов любой другой строки, умноженных на ненулевое число
5) вычеркивание нулевой строки.
Действительно, любая из этих операций переводит нулевые миноры в нулевые, а ненулевые – в ненулевые. Матрица, полученная в результате, не равна исходной, но имеет тот же ранг.
Пример. Найдем ранг матрицы 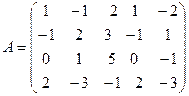 . Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице А эквивалентные преобразования. Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0. Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей – разность третьей и удвоенной первой:
. Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице А эквивалентные преобразования. Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0. Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей – разность третьей и удвоенной первой:
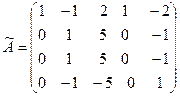
 .
.
Затем из третьей строки вычтем вторую, а к четвертой прибавим вторую:
 .
.
После вычеркивания нулевых строк получим матрицу размерности 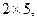 для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2:
для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2:
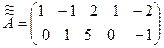 .
.
Ее минор 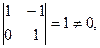 следовательно,
следовательно, 
Теорема о ранге.
Определение 4.3. Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы.
Определение 4.4. Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).
В противном случае строки (столбцы) называются линейно независимыми.
Замечание. Можно доказать, что необходимым и достаточным условием линейной зависимости строк матрицы является то, что одна из них является линейной комбинацией остальных.
Теорема 4.1. Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией этих строк (столбцов).
Доказательство (для строк).
1. Если бы базисные строки были линейно зависимыми, то с помощью эквивалентных преобразований из них можно было бы получить нулевую строку, что противоречит условию, что базисный минор не равен 0.
2. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0.
Докажем это свойство для строки, не входящей в базисный минор.
Добавим к базисному минору эту строку (пусть ее номер – k) и любой столбец матрицы (пусть его номер – j). Затем разложим полученный определитель, равный 0 (так как его порядок больше ранга матрицы) по j-му столбцу:
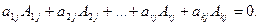 Поскольку
Поскольку 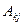 является базисным минором,
является базисным минором, 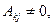 поэтому, разделив полученное равенство на
поэтому, разделив полученное равенство на 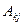 , найдем, что
, найдем, что
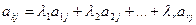 для всех j=1,2,…,n, где
для всех j=1,2,…,n, где 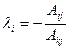 . Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана.
. Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана.
Совместность линейных систем.
Определение 4.5. Линейная система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Определение 4.6. Совместная линейная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Назовем расширенной матрицей системы (2.2) матрицу вида
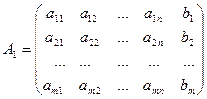 , а матрицей системы – матрицу из коэффициентов при неизвестных.
, а матрицей системы – матрицу из коэффициентов при неизвестных.
Теорема 4.2 (теорема Кронекера-Капелли). Система (2.2) совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы.
Доказательство.
1) Необходимость: пусть система (2.2) совместна и 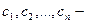 ее решение. Тогда
ее решение. Тогда
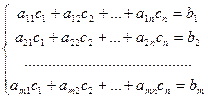 , (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть
, (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть 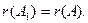
2) Достаточность: если 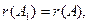 то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации
то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации 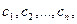 то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.
то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.
Общее решение однородной линейной системы.
Рассмотрим однородную линейную систему
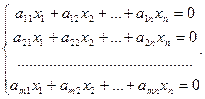 . (4.2)
. (4.2)
Отметим, что такая система всегда совместна, поскольку имеет нулевое решение 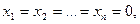 называемое тривиальным.
называемое тривиальным.
Пусть ранг матрицы системы r<n. Предположим, что в базисный минор входят коэффициенты первых r уравнений. Тогда оставшиеся m – r уравнений являются линейными комбинациями, то есть следствиями предыдущих. Поэтому можно оставить в системе только первые r уравнений:
. 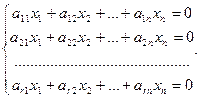
Оставим в левой части каждого уравнения неизвестные, коэффициенты при которых входят в базисный минор, а остальные неизвестные перенесем направо:
 (4.3)
(4.3)
Эта система будет иметь единственное решение относительно неизвестных 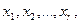 выражающее их через остальные неизвестные (
выражающее их через остальные неизвестные (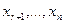 ), которым можно придавать любые произвольные значения. Таким образом, система (4.2) при r<n является неопределенной.
), которым можно придавать любые произвольные значения. Таким образом, система (4.2) при r<n является неопределенной.
Определение 4.7. Неизвестные 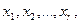 коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные (
коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные (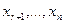 ) – свободными неизвестными.
) – свободными неизвестными.
Определение 4.8. Решения системы (4.2) 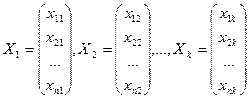 (4.4) называются линейно независимыми, если линейная комбинация
(4.4) называются линейно независимыми, если линейная комбинация 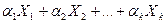 дает нулевой столбец только при
дает нулевой столбец только при 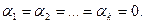
Покажем, что число линейно независимых решений системы (4.2) равно n – r. Действительно, рассмотрим столбцы вида
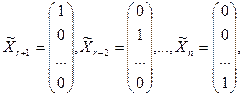 (4.5) содержащие по n-r чисел. Очевидно, что эти столбцы линейно независимы, а любой другой столбец той же размерности является их линейной комбинацией. Пусть эти столбцы задают значения свободных неизвестных системы (4.2).
(4.5) содержащие по n-r чисел. Очевидно, что эти столбцы линейно независимы, а любой другой столбец той же размерности является их линейной комбинацией. Пусть эти столбцы задают значения свободных неизвестных системы (4.2).
Тогда базисные неизвестные будут однозначно определяться для выбранных свободных неизвестных из системы (4.3) по правилу Крамера, и все решения системы, соответствующие наборам свободных неизвестных (4.5), образуют n-r линейно независимых столбцов вида (4.4), то есть n-r линейно независимых решений системы (4.2).
Определение 4.9. Любые n – r линейно независимых решений системы (4.2) называются ее фундаментальной системой решений.
Определение 4.10. Фундаментальная система решений линейной однородной системы, в которой свободные неизвестные задаются по формулам (4.5), называется нормальной фундаментальной системой решений.
Замечание. Очевидным образом доказываются свойства решений однородной линейной системы (4.2):
Свойство 1. Сумма решений системы (4.2) является ее решением.
Свойство 2. Столбец решений (4.2), умноженный на любое число, тоже есть решение этой системы.
Следовательно, любая линейная комбинация фундаментальной системы решений системы (4.2) является ее решением. Можно доказать и обратное утверждение:
Теорема 4.3 (без доказательства). Любое решение однородной линейной системы (4.2) является линейной комбинацией фундаментальной системы ее решений.
Таким образом, любое решение системы (4.2) имеет вид:
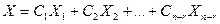 , где
, где 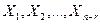 - фундаментальная система решений.
- фундаментальная система решений.
Пример.
Решим систему 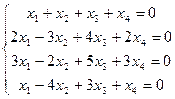 . Найдем ранг матрицы системы
. Найдем ранг матрицы системы 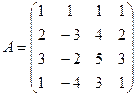 . Преобразуем ее к виду:
. Преобразуем ее к виду: 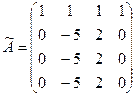 . Очевидно, что r(A)=2.
. Очевидно, что r(A)=2.
Пусть 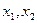 - базисные неизвестные,
- базисные неизвестные, 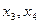 - свободные неизвестные. Заменим исходную систему системой из первых двух уравнений, коэффициенты которых входят в базисный минор, и перенесем базисные неизвестные в правые части уравнений:
- свободные неизвестные. Заменим исходную систему системой из первых двух уравнений, коэффициенты которых входят в базисный минор, и перенесем базисные неизвестные в правые части уравнений:
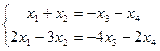 . Пусть
. Пусть 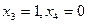 . Тогда
. Тогда 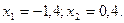 Если
Если 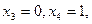
то 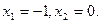 Получена фундаментальная система решений:
Получена фундаментальная система решений: 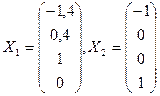 .
.
Теперь общее решение системы можно записать в виде: 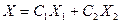 , где С1 и С2 – любые произвольные числа.
, где С1 и С2 – любые произвольные числа.
Структура общего решения неоднородной линейной системы.
Рассмотрим неоднородную линейную систему (2.2):
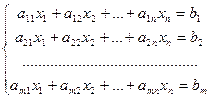 .
.
Докажем следующие свойства ее решений:
Свойство 1. Сумма любого решения системы (2.2) и любого решения соответствующей однородной системы (4.2) является решением системы (2.2).
Доказательство.
Пусть с1, с2,…,с n – решение системы (2.2), а d1, d2,…, dn – решение системы (4.2) с теми же коэффициентами при неизвестных. Подставим в систему (2.2) xi= ci+ di:
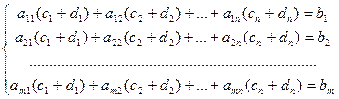 .
.
После перегруппировки слагаемых получим:
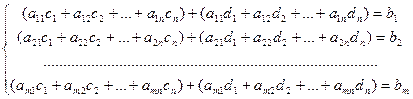 .
.
Но  Следовательно, xi= ci+ di является решением системы (2.2).
Следовательно, xi= ci+ di является решением системы (2.2).
Свойство 2. Разность любых двух решений неоднородной системы (2.2) является решением соответствующей однородной системы (4.2).
Доказательство.
Пусть 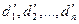 и
и 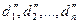 - решения системы (2.2). Тогда
- решения системы (2.2). Тогда
 Утверждение доказано.
Утверждение доказано.
Следствие. Общее решение неоднородной системы (2.2) представляет собой сумму общего решения соответствующей однородной системы (4.2) и частного решения системы (2.2).
Пример.
Общее решение системы 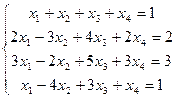 можно записать в виде:
можно записать в виде:
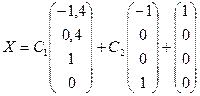 , где
, где 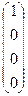 - частное решение данной системы.
- частное решение данной системы.
Лекция 5.
Векторы. Линейные операции над векторами. Проекция вектора на ось. Декартовы координаты векторов и точек. Скалярное произведение векторов, его основные свойства, координатное выражение.
Определение 5.1. Вектором называется направленный отрезок.
Обозначения: a, 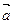 ,
, 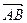 .
.
Определение 5.2. Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Вектор называется нулевым, если его начальная и конечная точки совпадают. Нулевой вектор не имеет определенного направлен




 - элемент матрицы,
- элемент матрицы,  номер строки, в которой стоит данный элемент,
номер строки, в которой стоит данный элемент, 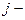 номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
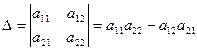 .
. 2.
2. 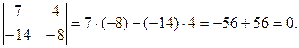
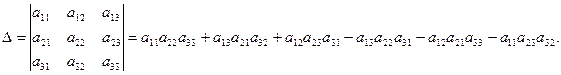












 образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:
образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: 




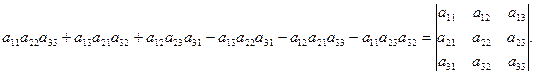

 .
.


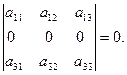

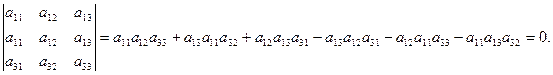
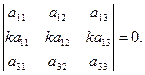
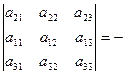

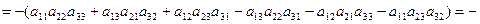
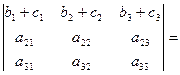
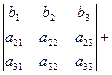

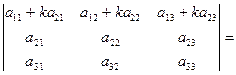
 выбранный элемент определителя,
выбранный элемент определителя, 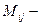 его минор.
его минор.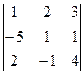
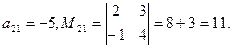
 элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е.
элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е. 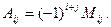
 где i=1,2,3.
где i=1,2,3.

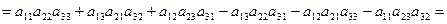
 с помощью разложения по первому столбцу. Заметим, что
с помощью разложения по первому столбцу. Заметим, что 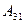 при этом искать не требуется, так как
при этом искать не требуется, так как 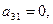 следовательно, и
следовательно, и  Найдем
Найдем 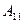 и
и 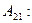
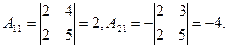 Следовательно,
Следовательно,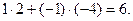

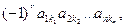 каждый из которых соответствует одному из n! упорядоченных множеств
каждый из которых соответствует одному из n! упорядоченных множеств  полученных r попарными перестановками элементов из множества 1,2,…,n.
полученных r попарными перестановками элементов из множества 1,2,…,n.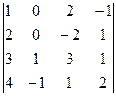 с помощью разложения по 2-му столбцу. Для этого найдем
с помощью разложения по 2-му столбцу. Для этого найдем  и
и 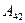 :
: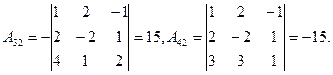 Следовательно,
Следовательно,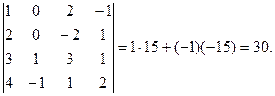
 где
где  числа,
числа,  переменные.
переменные.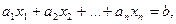 (2.1)
(2.1)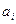 и b – числа,
и b – числа,  - неизвестные.
- неизвестные.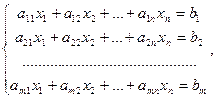 (2.2)
(2.2)  - числа,
- числа,  - неизвестные, n – число неизвестных, m – число уравнений.
- неизвестные, n – число неизвестных, m – число уравнений. которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.
которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.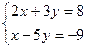 . Единственным решением является пара чисел х = 1, у = 2.
. Единственным решением является пара чисел х = 1, у = 2. . Решением этой системы будут любые два числа х и у, удовлетворяющие условию у = 3 – х. Например, х=1, у=2; х=0, у=3 и т. д.
. Решением этой системы будут любые два числа х и у, удовлетворяющие условию у = 3 – х. Например, х=1, у=2; х=0, у=3 и т. д.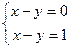 . Очевидно, что эта система не имеет решений, так как разность двух чисел не может принимать двух различных значений.
. Очевидно, что эта система не имеет решений, так как разность двух чисел не может принимать двух различных значений.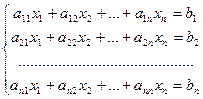 (2.3)
(2.3)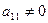 (этого всегда можно добиться, поменяв уравнения местами). Разделим обе части первого уравнения на
(этого всегда можно добиться, поменяв уравнения местами). Разделим обе части первого уравнения на 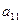 и вычтем полученное уравнение из каждого из остальных уравнений системы, умножив его предварительно на
и вычтем полученное уравнение из каждого из остальных уравнений системы, умножив его предварительно на 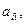 где i – номер очередного уравнения. Как известно, полученная при этом новая система будет равносильна исходной. Коэффициенты при
где i – номер очередного уравнения. Как известно, полученная при этом новая система будет равносильна исходной. Коэффициенты при  во всех уравнениях этой системы, начиная со второго, будут равны 0, т.е. система выглядит так:
во всех уравнениях этой системы, начиная со второго, будут равны 0, т.е. система выглядит так: .
. из третьего и последующих уравнений. Продолжая эту операцию для следующих неизвестных, приведем систему к так называемому треугольному виду:
из третьего и последующих уравнений. Продолжая эту операцию для следующих неизвестных, приведем систему к так называемому треугольному виду: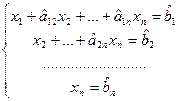 . (2.4)
. (2.4) и
и 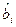 обозначены изменившиеся в результате преобразований числовые коэффициенты и свободные члены.
обозначены изменившиеся в результате преобразований числовые коэффициенты и свободные члены. , а затем последовательной подстановкой – остальные неизвестные.
, а затем последовательной подстановкой – остальные неизвестные.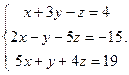
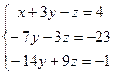 . Теперь вычтем из третьего уравнения удвоенное второе, а затем разделим второе уравнение на –7 (коэффициент при у), а третье – на 15 (новый коэффициент при z). Система примет вид:
. Теперь вычтем из третьего уравнения удвоенное второе, а затем разделим второе уравнение на –7 (коэффициент при у), а третье – на 15 (новый коэффициент при z). Система примет вид: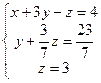 . Отсюда z=3, y=2, x=1 – единственное решение системы.
. Отсюда z=3, y=2, x=1 – единственное решение системы. после исключения х из второго и третьего уравнений примет вид:
после исключения х из второго и третьего уравнений примет вид: 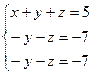 . Если затем вычесть второе уравнение из третьего, то последнее уравнение станет тождеством 0=0. В системе осталось два уравнения:
. Если затем вычесть второе уравнение из третьего, то последнее уравнение станет тождеством 0=0. В системе осталось два уравнения:  . Ее решение можно записать в виде: х = -2, у – любое число, z = 7 – y. Таким образом, система имеет бесконечно много решений.
. Ее решение можно записать в виде: х = -2, у – любое число, z = 7 – y. Таким образом, система имеет бесконечно много решений. . Применив к этой системе метод Гаусса, получим
. Применив к этой системе метод Гаусса, получим 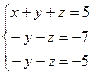 ,
,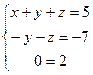 . Последнее равенство является неверным при любых значениях неизвестных, следовательно, система не имеет решения.
. Последнее равенство является неверным при любых значениях неизвестных, следовательно, система не имеет решения. , элементами которого являются коэффициенты при неизвестных:
, элементами которого являются коэффициенты при неизвестных:
 Умножим каждое уравнение системы (2.3) на алгебраические дополнения
Умножим каждое уравнение системы (2.3) на алгебраические дополнения 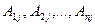 элементов j-го столбца
элементов j-го столбца 
 . (2.5)
. (2.5) .
. и равен
и равен 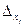 . Рассматривая j = 1,2 ,…, n, получим систему, эквивалентную исходной:
. Рассматривая j = 1,2 ,…, n, получим систему, эквивалентную исходной: 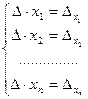 (2.6). Разделив все уравнения на
(2.6). Разделив все уравнения на 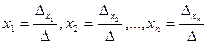 .
. .
.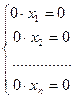 и имеет бесконечно много решений. Если же хотя бы один из
и имеет бесконечно много решений. Если же хотя бы один из  система решений не имеет.
система решений не имеет.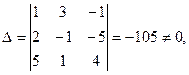 следовательно, система имеет единственное решение.
следовательно, система имеет единственное решение.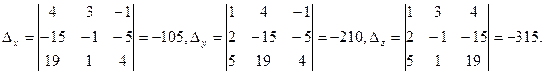

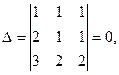 поскольку имеет два одинаковых столбца.
поскольку имеет два одинаковых столбца. и
и 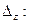
 поэтому система имеет бесконечно много решений.
поэтому система имеет бесконечно много решений.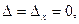 но
но 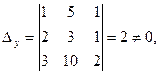
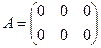 , r(A)=0.
, r(A)=0.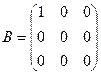 . Матрица В содержит единственный ненулевой элемент -
. Матрица В содержит единственный ненулевой элемент - 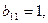 являющийся минором 1-го порядка. Все определители более высоких порядков, составленные из элементов этой матрицы, будут содержать 0-ю строку и поэтому равны 0. Следовательно, r(B)=1.
являющийся минором 1-го порядка. Все определители более высоких порядков, составленные из элементов этой матрицы, будут содержать 0-ю строку и поэтому равны 0. Следовательно, r(B)=1.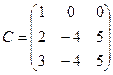 . Единственным минором 3-го порядка является определитель матрицы С, но он равен 0, поскольку содержит пропорциональные столбцы. Следовательно, r(C)<3.
. Единственным минором 3-го порядка является определитель матрицы С, но он равен 0, поскольку содержит пропорциональные столбцы. Следовательно, r(C)<3.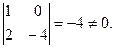 Значит, r(C)=2.
Значит, r(C)=2.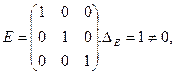 следовательно, r(E)=3.
следовательно, r(E)=3.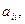 равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся:
равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся: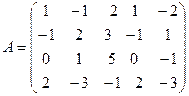 . Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице А эквивалентные преобразования. Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0. Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей – разность третьей и удвоенной первой:
. Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице А эквивалентные преобразования. Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0. Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей – разность третьей и удвоенной первой: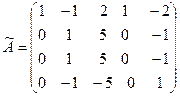
 .
.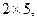 для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2:
для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2: 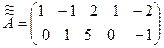 .
.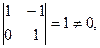 следовательно,
следовательно, 
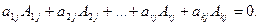 Поскольку
Поскольку 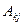 является базисным минором,
является базисным минором, 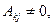 поэтому, разделив полученное равенство на
поэтому, разделив полученное равенство на 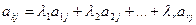 для всех j=1,2,…,n, где
для всех j=1,2,…,n, где 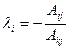 . Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана.
. Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана.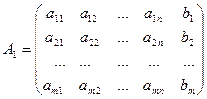 , а матрицей системы – матрицу из коэффициентов при неизвестных.
, а матрицей системы – матрицу из коэффициентов при неизвестных.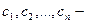 ее решение. Тогда
ее решение. Тогда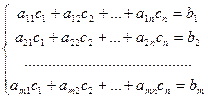 , (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть
, (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть 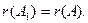
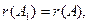 то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации
то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации 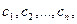 то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.
то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.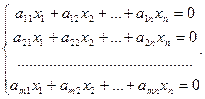 . (4.2)
. (4.2)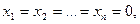 называемое тривиальным.
называемое тривиальным.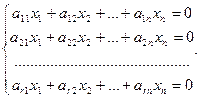
 (4.3)
(4.3)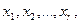 выражающее их через остальные неизвестные (
выражающее их через остальные неизвестные (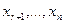 ), которым можно придавать любые произвольные значения. Таким образом, система (4.2) при r<n является неопределенной.
), которым можно придавать любые произвольные значения. Таким образом, система (4.2) при r<n является неопределенной.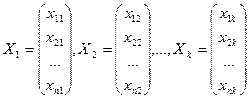 (4.4) называются линейно независимыми, если линейная комбинация
(4.4) называются линейно независимыми, если линейная комбинация 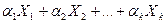 дает нулевой столбец только при
дает нулевой столбец только при 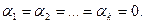
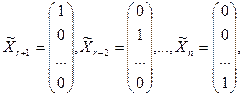 (4.5) содержащие по n-r чисел. Очевидно, что эти столбцы линейно независимы, а любой другой столбец той же размерности является их линейной комбинацией. Пусть эти столбцы задают значения свободных неизвестных системы (4.2).
(4.5) содержащие по n-r чисел. Очевидно, что эти столбцы линейно независимы, а любой другой столбец той же размерности является их линейной комбинацией. Пусть эти столбцы задают значения свободных неизвестных системы (4.2).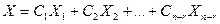 , где
, где 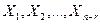 - фундаментальная система решений.
- фундаментальная система решений.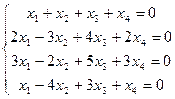 . Найдем ранг матрицы системы
. Найдем ранг матрицы системы 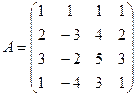 . Преобразуем ее к виду:
. Преобразуем ее к виду: 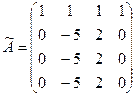 . Очевидно, что r(A)=2.
. Очевидно, что r(A)=2.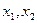 - базисные неизвестные,
- базисные неизвестные, 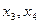 - свободные неизвестные. Заменим исходную систему системой из первых двух уравнений, коэффициенты которых входят в базисный минор, и перенесем базисные неизвестные в правые части уравнений:
- свободные неизвестные. Заменим исходную систему системой из первых двух уравнений, коэффициенты которых входят в базисный минор, и перенесем базисные неизвестные в правые части уравнений: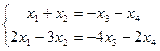 . Пусть
. Пусть 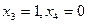 . Тогда
. Тогда 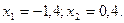 Если
Если 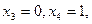
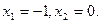 Получена фундаментальная система решений:
Получена фундаментальная система решений: 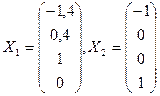 .
.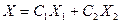 , где С1 и С2 – любые произвольные числа.
, где С1 и С2 – любые произвольные числа.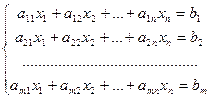 .
.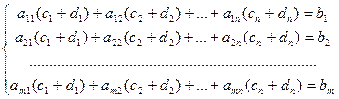 .
.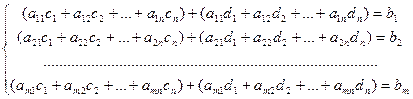 .
. Следовательно, xi= ci+ di является решением системы (2.2).
Следовательно, xi= ci+ di является решением системы (2.2).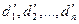 и
и 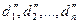 - решения системы (2.2). Тогда
- решения системы (2.2). Тогда Утверждение доказано.
Утверждение доказано.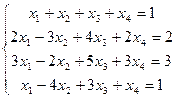 можно записать в виде:
можно записать в виде: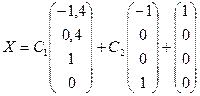 , где
, где 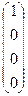 - частное решение данной системы.
- частное решение данной системы.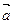 ,
,  .
.


