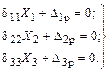Симметричная основная система – основная система, в которой неизвестные силовые факторы размещаются по оси симметрии.
В симметричной основной системе получаем основные неизвестные в виде симметричных и кососимметричных силовых факторов.
Рассмотрим некоторое произвольное сечение, в котором под воздействием внешней нагрузки возникают 6 силовых факторов (рисунок 3.22).

Рисунок 3.22 – Силовые факторы, возникающие в произвольном сечении рамы
В правой и левой плоскостях произведенного сечения силы и моменты равны, но направлены в разные стороны.
Под симметричными силовыми факторами понимают такие, которые образуют зеркальное отображение относительно плоскости сечения. Силовые факторы, каждый из которых противоположен по знаку зеркальному отображению взаимного фактора, являются кососимметричными.
Тогда, на рисунке 3.22:
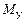 ,
, 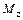 , N – симметричные силовые факторы;
, N – симметричные силовые факторы;
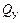 ,
, 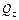 ,
,  – кососимметричные силовые факторы.
– кососимметричные силовые факторы.
Симметричные силовые факторы дают симметричные эпюры, а кососимметричные – кососимметричные эпюры. Т.е. получаем взаимно нулевые эпюры.
Правило 1. Коэффициенты канонических уравнений 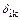 , у которых один индекс принадлежит симметричному фактору, а другой – кососимметричному фактору, обращаются в нуль. И их сразу можно вычеркнуть из системы канонических уравнений.
, у которых один индекс принадлежит симметричному фактору, а другой – кососимметричному фактору, обращаются в нуль. И их сразу можно вычеркнуть из системы канонических уравнений.
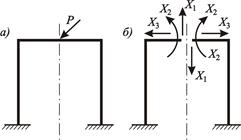
Рассмотрим симметричную раму (рисунок 3.23, а).
| Рисунок 3.23 – Упрощение расчета рамы с помощью выбора симметричной основной системы:
а – исходная система; б – симметричная основная система
| |
Система канонических уравнений для этой рамы в общем случае нагружения будет иметь вид:
 (3.24)
(3.24)
Симметричная основная система для рассматриваемой рамы показана на рисунке 3.23, б.
В приведенной основной системе: Х 1 – кососимметричный силовой фактор; Х 2, Х 3 – симметричные силовые факторы.
В соответствии с правилом 1: 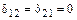 и
и 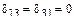 .
.
Тогда, система канонических уравнений (3.24) будет иметь вид:
 (3.25)
(3.25)
В результате система из трех уравнений распадается на две независимые системы, одна из которых относится к симметричным силовым факторам, другая – к кососимметричным. Решение двух систем проще, чем решение полной системы.
Таким образом, выбор симметричной основной системы позволяет решение системы из n уравнений с n неизвестными заменить решением двух независимых систем. Это сокращает объем вычислений.
П р и м е ч а н и я:
1 Если заданная система является симметричной, то и основную систему надо всегда выбирать симметричной.
2 Выбор симметричной основной системы позволяет получить основные неизвестные в виде симметричных и кососимметричных силовых факторов, которые дают соответственно симметричные и кососимметричные эпюры.
3 В результате обращения в нуль коэффициентов канонических уравнений с индексами, принадлежащими симметричным и кососимметричным силовым факторам, происходит распад полной системы уравнений на две независимые системы.
3.8.2 Преобразование нагрузки
При использовании способа преобразования нагрузки лишние неизвестные целесообразно располагать на оси симметрии системы.
Правило 2. Любую несимметричную нагрузку, действующую на симметричную раму, можно разложить на симметричную и кососимметричную составляющие (рисунок 3.24).
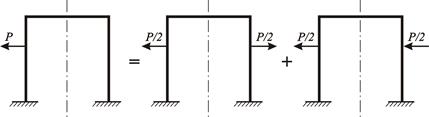
Рисунок 3.24 – Представление несимметричной нагрузки в виде суммы
симметричной и кососимметричной составляющих
Расчет выполняется отдельно на действие каждой из них. Результирующая эпюра, например, моментов получается путем алгебраического суммирования ординат двух эпюр
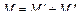 ,
,
где 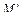 ,
, 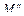 – окончательные эпюры изгибающих моментов от действия симметричной и кососимметричной нагрузки соответственно.
– окончательные эпюры изгибающих моментов от действия симметричной и кососимметричной нагрузки соответственно.
Для несимметричной нагрузки при симметричной основной системе будут верны уравнения (3.25).
Правило 3. При симметричной внешней нагрузке, действующей на симметричную раму, кососимметричные силовые факторы, ( ,
, 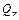 ,
,  ) в плоскости симметрии обращаются в нуль.
) в плоскости симметрии обращаются в нуль.
В соответствии с правилом 3: Х 1 = 0.
Тогда, уравнения (3.25) можно записать в виде

Правило 4. При кососимметричной внешней нагрузке, действующей на симметричную раму, симметричные силовые факторы (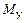 ,
, 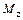 , N) в плоскости симметрии обращаются в нуль.
, N) в плоскости симметрии обращаются в нуль.
В соответствии с правилом 4: Х 2 = Х 3 = 0.
Следовательно, уравнения (3.25) можно будет записать в виде:
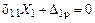 .
.
П р и м е ч а н и е – Сущность рассмотренного способа упрощения расчета симметричной статически неопределимой системы состоит в разложении несимметричной нагрузки на симметричную и кососимметричную составляющие. Поскольку расчет на каждую составляющую нагрузки производится раздельно, то вместо одной системы уравнений с полным числом неизвестных получаем де независимые системы, одна из которых содержит только симметричные силовые факторы, другая – кососимметричные.
Правило 5. Расчет симметричной многопролетной рамы, на которую действует симметричная или кососимметричная внешняя нагрузка, можно упростить, рассматривая половину рамы – при одной оси симметрии и 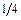 часть рамы – при двух осях симметрии.
часть рамы – при двух осях симметрии.
В местах разреза вводятся связи, соответствующие тем силовым факторам, которые возникают в сечении.
Рассмотрим трехпролетную симметричную раму, загруженную симметричной нагрузкой (рисунок 3.25, а) и кососимметричной (рисунок 3.26, а). Рама девять раз статически неопределима.
На рисунках 3.25, б и 3.26, б приведены упрощенные расчетные схемы 1/2 части рамы для рассматриваемых вариантов нагружения.
Действие отброшенной части на оставшуюся учитывается введением соответствующих опорных закреплений (связей).
| Рисунок 3.25 – Упрощение расчета симметричной рамы, загруженной симметричной нагрузкой:
а – исходная система; б – 1/2 часть рамы; в – схема для расчета числа лишних неизвестных 1/2 части рамы
| |
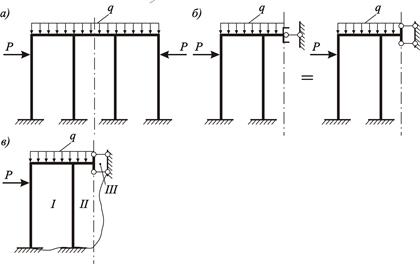

Рисунок 3.26 – Упрощение расчета симметричной рамы, загруженной
кососимметричной нагрузкой:
а – исходная система; б – 1/2 часть рамы; в – схема для расчета числа лишних неизвестных
1/2 части рамы
На расчётной схеме 1/2 части рамы, загруженной симметричной нагрузкой (см. рисунок 3.25, б), квадратной скобкой и горизонтальным стержнем с шарнирами по концам обозначены связи, закрепляющие сечение соответственно от поворотов в вертикальной плоскости и горизонтальных перемещений, т.е. от перемещений по направлению ненулевых внутренних усилий, которые возникают в сечении по оси симметрии.
Связи, закрепляющие сечения от вертикальных перемещений, не показаны, так как поперечные силы в плоскости симметрии равны нулю (правило 3).
При действии на раму кососимметричной нагрузки в месте разреза рамы введена связь в виде вертикального стержня с шарнирами по концам, закрепляющего сечение от вертикальных смещений (см. рисунок 3.26, б). Связи, соответствующие изгибающему моменту и нормальной силе, в плоскости симметрии равны нулю (правило 4).
Степень статической неопределимости 1/2 части рамы для рассматриваемых вариантов загружения снижается соответственно до пяти и четырех.
На рисунках 3.25, в и 3.26, в приведены схемы, поясняющие расчет степени статической неопределимости 1/2 части рам, с использованием формулы (3.3). Римскими цифрами на схемах обозначены номера контуров.
Рассматриваемый способ уменьшения степени статической неопределимости системы широко используется при расчете стержневых вагонных конструкций.
П р и м е ч а н и я:
1 Симметричность конструкции в сочетании с симметричностью или кососимметричностью внешней нагрузки позволяют уменьшить степень статической неопределимости системы за счет рассмотрения 1/2 или 1/4 части конструкции.
2 При выделении 1/2 или 1/4 части конструкции действие отброшенной части на оставшуюся компенсируется введением в местах разреза связей от ненулевых силовых факторов. При действии симметричной нагрузки на оси симметрии вводятся связи от симметричных силовых факторов, при действии кососимметричной нагрузки – от кососимметричных силовых факторов.
3 Выделенная 1/2 или 1/4 части конструкции с приложенной к ней внешней нагрузкой и введенными связями, рассматривается как самостоятельная расчетная схема.
Группировка неизвестных
При расчете многопролетных симметричных рам не всегда удается разместить все неизвестные в сечениях по оси симметрии.
В этом случае для получения симметричных и кососимметричных эпюр целесообразно принимать групповые неизвестные, расположив их в различных симметрично расположенных точках.
Проиллюстрируем данный способ для двухпролетной рамы, приведенной на рисунке 3.27, а.
При традиционном способе решения основная система и единичные эпюры показаны на рисунках 3.27, б–г.
При использовании традиционного способа все побочные коэффициенты 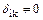 .
.
При использовании способа группировки неизвестных упрощение расчета обеспечивается тем, что в качестве лишних неизвестных принимают не отдельные силы, а группы сил.

Рисунок 3.27 – Традиционный способ решения системы:
а – исходная система; б – основная система; в, г – единичные эпюры моментов
П р и м е ч а н и е – Групповые неизвестные подбирают так, чтобы получающиеся от их действия эпюры были ортогональными (симметричными и кососимметричными).
Для рамы, изображенной на рисунке 3.27, а, реакции удаленных связей, которые обозначим как 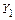 и
и 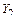 , заменим эквивалентными им новыми неизвестными – парами симметричных
, заменим эквивалентными им новыми неизвестными – парами симметричных 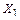 и кососимметричных
и кососимметричных  сил. Реакцию левой опоры
сил. Реакцию левой опоры 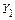 представим суммой сил
представим суммой сил 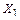 и
и  , а реакция правой опоры
, а реакция правой опоры  – разностью этих сил (рисунок 3.28, а), т.е.
– разностью этих сил (рисунок 3.28, а), т.е.
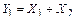 ;
; 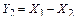 .
.
П р и м е ч а н и е – Неизвестное 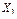 представляет собой две симметрично расположенные силы, а
представляет собой две симметрично расположенные силы, а 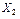 – две кососимметричные силы.
– две кососимметричные силы.
Эпюры моментов от единичных групповых силовых факторов показаны на рисунках 3.28, б, в.
В результате перемножения эпюр 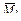 и
и 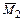 получаем
получаем  . Это следует также из правила 1.
. Это следует также из правила 1.
В результате получаем канонические уравнения с полностью разделенными неизвестными, каждое из которых содержит только по одному лишнему неизвестному
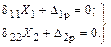
Использование групповых неизвестных значительно упрощает расчет симметричных рам с большим числом лишних неизвестных.
П р и м е ч а н и е – Сущность способа группировки неизвестных состоит в том, что в качестве неизвестных принимают не отдельные силы, а группы сил, составленные так, чтобы получающиеся от их действия эпюры были ортогональными.

Рисунок 3.28 – Упрощение расчета рамы с помощью способа группировки
неизвестных:
а – основная система; б, в – единичные эпюры моментов
Введение жестких консолей
Этот способ применяется для рам, имеющих замкнутый контур (см. рисунки 3.1, в и 3.2, в), и позволяет получать системы канонических уравнений с полностью разделенными неизвестными
Рассмотрим систему, показанную на рисунке 3.1, в.
В случае выбора традиционной симметричной основной системы (рисунок 3.29, а) для нее будет справедлива система уравнений (3.25), в которой 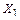 – кососимметричный силовой фактор,
– кососимметричный силовой фактор, 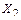 ,
, 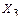 – симметричные силовые факторы.
– симметричные силовые факторы.
Тогда, побочные коэффициенты  и
и 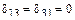 .
.
В полученных уравнениях все побочные коэффициенты, кроме коэффициентов  и
и 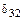 равны нулю, т.е.
равны нулю, т.е. 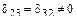 .
.
Для получения системы уравнений с полностью разделенными неизвестными необходимо также обратить в нуль и коэффициенты 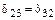 с индексами, принадлежащими симметричным факторам.
с индексами, принадлежащими симметричным факторам.
Коэффициенты 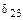 и
и  являются результатом перемножения единичных эпюр
являются результатом перемножения единичных эпюр 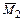 и
и 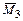 .
.
Для ортогонализации (обращения в нуль) этих эпюр необходимо перенести неизвестные в точку C, называемую упругим центром, с помощью жестких консолей.
П р и м е ч а н и е – При наличии у рамы одной оси симметрии упругий центр будет лежать на этой оси и надо будет определить только одну его координату zо.
Для рамы, имеющей две оси симметрии, упругий центр будет находиться на пересечении этих осей.

Рисунок 3.29 – Упрощение расчета рамы введением жестких консолей:
а – симметричная основная система; б – основная система с введенными жесткими консолями; в, г – единичные эпюры моментов
На рисунках 3.29, б-г приведены основная система, полученная с помощью введения абсолютно жестких консолей и перемещения неизвестных силовых факторов в упругий центр, а также единичные эпюры моментов 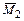 и
и 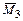 .
.
Коэффициент 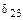 , определяемый как результат перемножения этих эпюр, будет равен
, определяемый как результат перемножения этих эпюр, будет равен
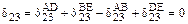 ,
,
где 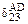 ,
,  – результат перемножения эпюр
– результат перемножения эпюр 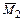 и
и 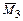 соответственно на участках AD и BE;
соответственно на участках AD и BE;
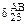 ,
,  – то же на участках AB и DE.
– то же на участках AB и DE.
Проанализируем результат перемножения эпюр по всем участкам рамы.
На участках AD и BE коэффициент  будет равен нулю (
будет равен нулю (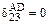 и
и 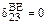 ), поскольку здесь перемножаются симметричные эпюры
), поскольку здесь перемножаются симметричные эпюры 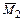 и кососимметричные
и кососимметричные 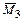 .
.
На участках AB и DE эпюры 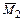 и
и  одинаковы по величине, но обратны по знаку. Соответственно в результате перемножения получаем
одинаковы по величине, но обратны по знаку. Соответственно в результате перемножения получаем 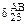 и
и  одинаковые по величине, но с разными знаками. При суммировании они дают нуль.
одинаковые по величине, но с разными знаками. При суммировании они дают нуль.
Таким образом, в рассматриваемом случае эпюры 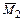 и
и 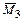 являются ортогональными.
являются ортогональными.
Тогда канонические уравнения примут вид
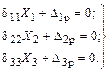
Таким образом, при переносе неизвестных в упругий центр обращается в нуль единственное оставшееся побочное перемещение 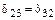 и вместо системы уравнений получается 3 независимых уравнения.
и вместо системы уравнений получается 3 независимых уравнения.






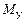 ,
, 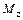 , N – симметричные силовые факторы;
, N – симметричные силовые факторы;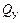 ,
, 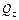 ,
,  – кососимметричные силовые факторы.
– кососимметричные силовые факторы.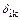 , у которых один индекс принадлежит симметричному фактору, а другой – кососимметричному фактору, обращаются в нуль. И их сразу можно вычеркнуть из системы канонических уравнений.
, у которых один индекс принадлежит симметричному фактору, а другой – кососимметричному фактору, обращаются в нуль. И их сразу можно вычеркнуть из системы канонических уравнений.
 (3.24)
(3.24)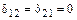 и
и 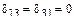 .
. (3.25)
(3.25)
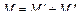 ,
,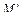 ,
, 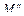 – окончательные эпюры изгибающих моментов от действия симметричной и кососимметричной нагрузки соответственно.
– окончательные эпюры изгибающих моментов от действия симметричной и кососимметричной нагрузки соответственно. ,
, 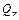 ,
, 
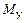 ,
, 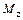 , N) в плоскости симметрии обращаются в нуль.
, N) в плоскости симметрии обращаются в нуль.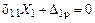 .
.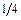 часть рамы – при двух осях симметрии.
часть рамы – при двух осях симметрии.

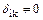 .
.
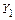 и
и 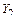 , заменим эквивалентными им новыми неизвестными – парами симметричных
, заменим эквивалентными им новыми неизвестными – парами симметричных 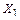 и кососимметричных
и кососимметричных  сил. Реакцию левой опоры
сил. Реакцию левой опоры 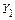 представим суммой сил
представим суммой сил 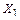 и
и  , а реакция правой опоры
, а реакция правой опоры  – разностью этих сил (рисунок 3.28, а), т.е.
– разностью этих сил (рисунок 3.28, а), т.е.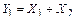 ;
; 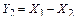 .
.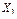 представляет собой две симметрично расположенные силы, а
представляет собой две симметрично расположенные силы, а 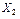 – две кососимметричные силы.
– две кососимметричные силы.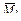 и
и 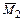 получаем
получаем  . Это следует также из правила 1.
. Это следует также из правила 1.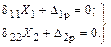

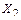 ,
, 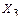 – симметричные силовые факторы.
– симметричные силовые факторы. и
и 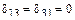 .
. и
и 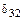 равны нулю, т.е.
равны нулю, т.е. 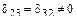 .
.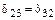 с индексами, принадлежащими симметричным факторам.
с индексами, принадлежащими симметричным факторам.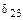 и
и  являются результатом перемножения единичных эпюр
являются результатом перемножения единичных эпюр 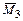 .
.
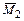 и
и 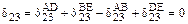 ,
, 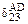 ,
,  – результат перемножения эпюр
– результат перемножения эпюр 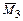 соответственно на участках AD и BE;
соответственно на участках AD и BE;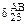 ,
,  – то же на участках AB и DE.
– то же на участках AB и DE. будет равен нулю (
будет равен нулю (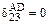 и
и 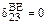 ), поскольку здесь перемножаются симметричные эпюры
), поскольку здесь перемножаются симметричные эпюры 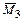 .
. одинаковы по величине, но обратны по знаку. Соответственно в результате перемножения получаем
одинаковы по величине, но обратны по знаку. Соответственно в результате перемножения получаем