Определение коэффициентов и свободных членов канонических уравнений. Коэффициенты и свободные членов канонических уравнений, являющиеся единичными и грузовыми перемещениями, вычисляются по формулам перемещений (интегралам Мора).
В случае плоской задачи
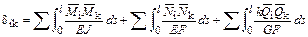 ; (3.10)
; (3.10)
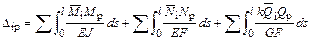 , (3.11)
, (3.11)
где 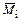 ,
, 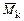 ,
, 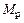 – изгибающие моменты в основной системе соответственно от действия силовых факторов
– изгибающие моменты в основной системе соответственно от действия силовых факторов  ,
, 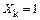 и от внешней нагрузки;
и от внешней нагрузки;
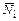 ,
, 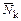 ,
, 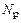 – то же продольные силы;
– то же продольные силы;
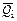 ,
, 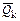 ,
,  – то же поперечные силы;
– то же поперечные силы;
 ,
,  ,
, 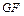 – жесткость стержней соответственно при деформациях изгиба, растяжения-сжатия и сдвига;
– жесткость стержней соответственно при деформациях изгиба, растяжения-сжатия и сдвига;
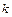 – коэффициент, зависящий от формы поперечного сечения.
– коэффициент, зависящий от формы поперечного сечения.
Примечания:
1. Интегрирование в формулах (3.10) и (3.11) производится в пределах длины каждого участка стержня, а суммирование – по всем участкам стержней рамы.
2. При использовании формул перемещений обычно не учитывают те слагаемые, влиянием которых можно пренебречь. Например, при расчете балок и рам пренебрегают деформациями растяжения-сжатия и сдвига.
3. В случае пространственной задачи формулы перемещений содержит не три, а шесть слагаемых (в соответствии с числом внутренних усилий, которые могут возникать в поперечных сечениях).
В практических расчетах для вычисления интегралов в формулах перемещений (3.10) и (3.11) необходимо построить эпюры 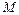 ,
, 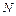 и
и 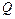 от единичных силовых факторов
от единичных силовых факторов 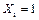 , …,
, …, 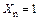 (единичные эпюры) и от внешней нагрузки (грузовые эпюры) и перемножить их по правилу Симпсона или Верещагина.
(единичные эпюры) и от внешней нагрузки (грузовые эпюры) и перемножить их по правилу Симпсона или Верещагина.
Для построения эпюр основную систему поочередно загружают единичными силовыми факторами  , …,
, …,  и внешней нагрузкой.
и внешней нагрузкой.
Перемножение эпюр производят по формулам:
· если одна из эпюр нелинейная (рисунок 3.13, а)
 ; (3.12)
; (3.12)
· если обе эпюры линейные (рисунок 3.13, б)

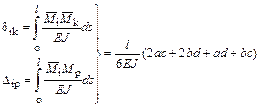 , (3.13)
, (3.13)
где a, b – значения ординат эпюры изгибающих моментов 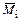 по концам участка стержня;
по концам участка стержня;
c, d – то же эпюр 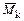 или
или 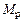 ;
;
e, f – то же посередине участка длиной l эпюр 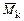 или
или 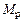 ;
;
l – длина участка стержня, на котором перемножаются эпюры.
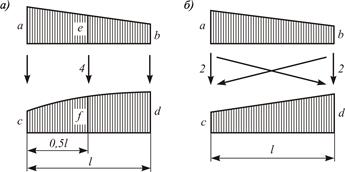
Рисунок 3.13 – Варианты перемножаемых эпюр:
а – линейная и нелинейная эпюры; б – две линейных эпюры
Частные случаи формулы (3.13):
· обе эпюры треугольные (рисунок 3.14, а)

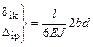 ;
;
· одна эпюра треугольная, другая – прямоугольная (рисунок 3.14, б)
 ;
;
· обе эпюры прямоугольные (рисунок3.14, в)
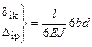 .
.
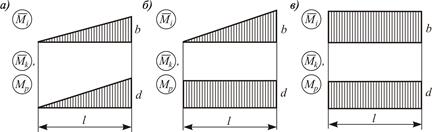
Рисунок 3.14 – Частные случаи перемножаемых линейных эпюр:
а – две треугольные эпюры; б – треугольная и прямоугольная эпюры;
в – две прямоугольные эпюры
Правило знаков при перемножении эпюр в приведенных формулах: произведения ординат эпюр, расположенных по одну сторону оси стержня, т.е. одного знака, берут со знаком плюс, а по разные стороны – со знаком минус.
При перемножении двух эпюр в виде «перекрученных» трапеций (рисунок 3.15) с учетом правила знаков имеем

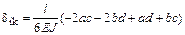 . (3.14)
. (3.14)
Примечания:
1 Индексы у коэффициентов и свободных членов показывают, какие эпюры перемножаются.
2 Главные коэффициенты 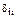 всегда положительны, побочные коэффициенты
всегда положительны, побочные коэффициенты 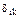 и свободные члены
и свободные члены 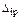 могут быть положительными, отрицательными и равными нулю. Отрицательное значение
могут быть положительными, отрицательными и равными нулю. Отрицательное значение  или
или 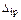 означает, что направление перемещения противоположно принятому направлению единичной силы Х i в основной системе.
означает, что направление перемещения противоположно принятому направлению единичной силы Х i в основной системе.
3 Если одна из перемножаемых эпюр имеет ломаное очертание, то ее разбивают на участки таким образом, чтобы она в пределах каждого участке была линейной, а жесткость сечения – постоянная (рисунок 3.16).
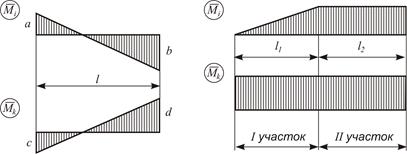
| Рисунок 3.15 – К учету правила знаков при перемножении эпюр
| Рисунок 3.16 – К разбиению перемножаемых эпюр на участки
|
Контроль правильности определения коэффициентов и свободных членов. Для проверки полученных коэффициентов и свободных членов строится суммарная единичная эпюра 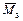 от совместного действия единичных силовых факторов
от совместного действия единичных силовых факторов 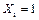 , …,
, …, 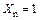 .
.
Ордината суммарной единичной эпюры
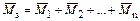 . (3.15)
. (3.15)
Универсальная проверка заключается в проверке выполнимости двух условий
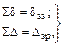 (3.16)
(3.16)
где 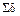 – сумма всех найденных коэффициентов при неизвестных,
– сумма всех найденных коэффициентов при неизвестных,
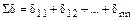 ;
;
 – сумма всех свободных членов,
– сумма всех свободных членов,
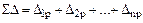 ;
;
 – перемещение, получаемое умножением эпюры
– перемещение, получаемое умножением эпюры 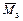 на саму себя;
на саму себя;
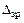 – перемещение, получаемое перемножением эпюр
– перемещение, получаемое перемножением эпюр  и
и 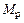 .
.
Если условия (3.16) не выполняются и расхождение между сравниваемыми величинами более 1%, то для отыскания ошибки рекомендуется производить построчную проверку по условию
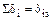 , (3.17)
, (3.17)
где 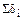 – сумма коэффициентов при неизвестных i -го уравнения,
– сумма коэффициентов при неизвестных i -го уравнения,
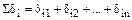 ;
;
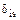 – перемещение, получаемое перемножением эпюр
– перемещение, получаемое перемножением эпюр 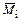 и
и 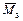 .
.
Решение канонических уравнений. Найденные и проверенные значения 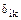 и
и 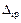 подставляют в канонические уравнения. Решают полученную систему уравнений относительно лишних неизвестных
подставляют в канонические уравнения. Решают полученную систему уравнений относительно лишних неизвестных 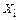 сокращенным способом Гаусса или с помощью ЭВМ, используя стандартную программу решения линейных алгебраических уравнений.
сокращенным способом Гаусса или с помощью ЭВМ, используя стандартную программу решения линейных алгебраических уравнений.



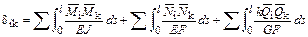 ; (3.10)
; (3.10)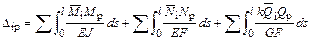 , (3.11)
, (3.11)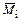 ,
, 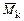 ,
, 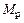 – изгибающие моменты в основной системе соответственно от действия силовых факторов
– изгибающие моменты в основной системе соответственно от действия силовых факторов  ,
, 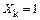 и от внешней нагрузки;
и от внешней нагрузки;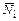 ,
, 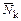 ,
, 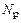 – то же продольные силы;
– то же продольные силы;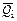 ,
, 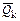 ,
,  – то же поперечные силы;
– то же поперечные силы; ,
,  ,
, 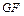 – жесткость стержней соответственно при деформациях изгиба, растяжения-сжатия и сдвига;
– жесткость стержней соответственно при деформациях изгиба, растяжения-сжатия и сдвига;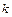 – коэффициент, зависящий от формы поперечного сечения.
– коэффициент, зависящий от формы поперечного сечения.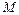 ,
, 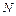 и
и 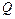 от единичных силовых факторов
от единичных силовых факторов 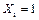 , …,
, …, 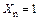 (единичные эпюры) и от внешней нагрузки (грузовые эпюры) и перемножить их по правилу Симпсона или Верещагина.
(единичные эпюры) и от внешней нагрузки (грузовые эпюры) и перемножить их по правилу Симпсона или Верещагина. , …,
, …,  и внешней нагрузкой.
и внешней нагрузкой. ; (3.12)
; (3.12)
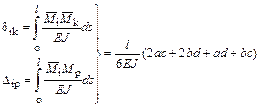 , (3.13)
, (3.13)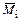 по концам участка стержня;
по концам участка стержня;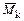 или
или 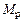 ;
;
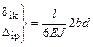 ;
; ;
;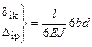 .
.
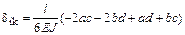 . (3.14)
. (3.14)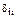 всегда положительны, побочные коэффициенты
всегда положительны, побочные коэффициенты 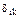 и свободные члены
и свободные члены 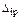 могут быть положительными, отрицательными и равными нулю. Отрицательное значение
могут быть положительными, отрицательными и равными нулю. Отрицательное значение  или
или 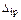 означает, что направление перемещения противоположно принятому направлению единичной силы Х i в основной системе.
означает, что направление перемещения противоположно принятому направлению единичной силы Х i в основной системе.
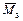 от совместного действия единичных силовых факторов
от совместного действия единичных силовых факторов 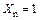 .
.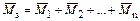 . (3.15)
. (3.15)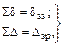 (3.16)
(3.16)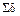 – сумма всех найденных коэффициентов при неизвестных,
– сумма всех найденных коэффициентов при неизвестных,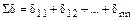 ;
; – сумма всех свободных членов,
– сумма всех свободных членов,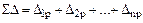 ;
; – перемещение, получаемое умножением эпюры
– перемещение, получаемое умножением эпюры 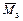 на саму себя;
на саму себя;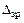 – перемещение, получаемое перемножением эпюр
– перемещение, получаемое перемножением эпюр  и
и 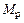 .
.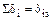 , (3.17)
, (3.17)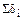 – сумма коэффициентов при неизвестных i -го уравнения,
– сумма коэффициентов при неизвестных i -го уравнения,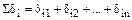 ;
;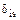 – перемещение, получаемое перемножением эпюр
– перемещение, получаемое перемножением эпюр 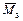 .
.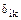 и
и 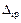 подставляют в канонические уравнения. Решают полученную систему уравнений относительно лишних неизвестных
подставляют в канонические уравнения. Решают полученную систему уравнений относительно лишних неизвестных 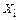 сокращенным способом Гаусса или с помощью ЭВМ, используя стандартную программу решения линейных алгебраических уравнений.
сокращенным способом Гаусса или с помощью ЭВМ, используя стандартную программу решения линейных алгебраических уравнений.


