

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Д-1 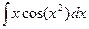 . Решение.
. Решение. 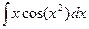 =
= 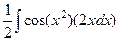 =
= 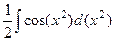 =
= 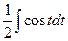 =
= 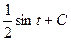 =
= 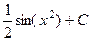 .
.
Ответ. 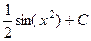 .
.
Д-2 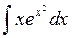 . Решение.
. Решение. 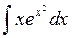 =
= 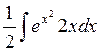 =
= 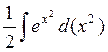 =
=  =
= 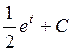 =
=  .
.
Ответ.  .
.
Д-3 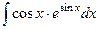 . Ответ.
. Ответ. 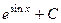 .
.
Д-4  . Ответ.
. Ответ.  .
.
Задача 284. Вычислить 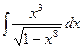 .
.
Решение.  =
= 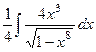 =
= 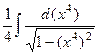 =
= 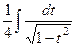 =
= 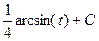 =
= 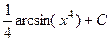 .
.
Ответ. 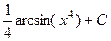 .
.
Задача 285. Вычислить  .
.
Решение. Если сразу подвести под знак дифференциала то, что есть в числителе, то будет  , но тогда в знаменателе получится выражение
, но тогда в знаменателе получится выражение  . чтобы не происходило такого усложнения и не появились вложенные квадратные корни, надо подводить не весь числитель, а отделить тот множитель, который нам удобнее, чтобы потом всё выражалось через
. чтобы не происходило такого усложнения и не появились вложенные квадратные корни, надо подводить не весь числитель, а отделить тот множитель, который нам удобнее, чтобы потом всё выражалось через 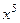 .
.
 =
= 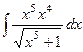 =
= 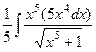 =
= 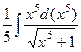
и теперь, после замены 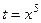 , получится
, получится  .
.
Далее, сделаем преобразование, котрое позволит оставить только однотипные корни:
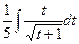 =
= 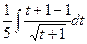 =
=  =
=
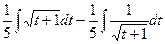 =
= 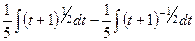
далее уже с помощью обычных действий со степенными функциями:
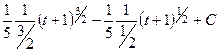 =
=  .
.
После обратной замены получаем ответ, при этом также заодно обратно меняем дробные степени на корни.
Ответ.  .
.
Задача 286. Вычислить  .
.
Решение.  =
=  =
=
= 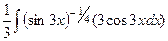 =
= 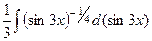 =
= 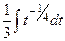 =
=
 =
= 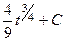 =
=  .
.
Ответ. 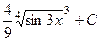 .
.
Задача 287. Вычислить 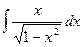 .
.
Решение. Несмотря на то, что интеграл похож на  , но, тем не менее, в числителе есть переменная
, но, тем не менее, в числителе есть переменная  , поэтому это не табличный интеграл, и ответ здесь вовсе не арксинус. Заметим, что в числителе 1-я степень, а под корнем в знаменателе 2-я. Домножим и поделим так, чтобы в числителе оказалось то выражение, которое под корнем в знаменателе.
, поэтому это не табличный интеграл, и ответ здесь вовсе не арксинус. Заметим, что в числителе 1-я степень, а под корнем в знаменателе 2-я. Домножим и поделим так, чтобы в числителе оказалось то выражение, которое под корнем в знаменателе.
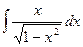 =
= 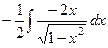 =
= 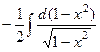
после замены переменной, это можно переписать так: 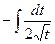
а значит, 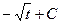 и после обратной замены:
и после обратной замены:
Ответ. 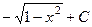 .
.
Задача 288. Вычислить 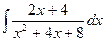 .
.
Решение. Заметим, что в числителе производная того выражения, которое есть в знаменателе. Тогда  =
= 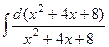 =
= 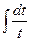 =
=  =
= 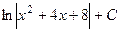 .
.
Здесь фактически мы применили замену 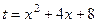 для упрощения выражения. Кстати, выделение полного квадрата в знаменателе это здесь был бы тупиковый путь, ведь в числителе не константа а многочлен, то есть не удалось бы свести к виду
для упрощения выражения. Кстати, выделение полного квадрата в знаменателе это здесь был бы тупиковый путь, ведь в числителе не константа а многочлен, то есть не удалось бы свести к виду 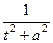 .
.
|
|
Ответ. 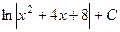 .
.
Задача 289. Вычислить 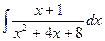 .
.
Решение. Здесь, в отличие от прошлой задачи, в числителе уже произвольный многочлен, не соответствующий производной от знаменателя. Тем не менее, можно путём арифметических операций получить там дифференциал знаменателя:
Домножим и поделим на 2, чтобы исправился коэффициент при  :
:
 =
= 
Теперь осталось прибавить и отнять 2, и будет получено 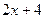 :
:
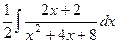 =
= 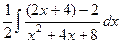 =
=
= 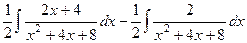 .
.
В первом слагаемом делается ровно то же самое, что в прошлой задаче, а во втором - выделить полный квадрат, и в итоге сводится к арктангенсу:
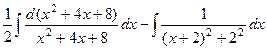 =
=
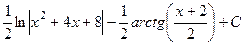 .
.
Ответ. 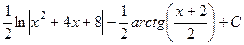 .
.
Задача 290. Вычислить интеграл  .
.
Решение.  =
=  =
= 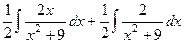
В отличие от прошлой задачи, здесь не надо прибавлять и вычитать, так как полный дифференциал знаменателя это 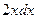 , в знаменателе нет 1-й степени, а его производная поэтому не содержит константу.
, в знаменателе нет 1-й степени, а его производная поэтому не содержит константу.
Далее, 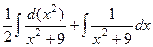 =
= 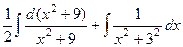 , и в итоге:
, и в итоге:
Ответ. 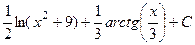 .
.
«Интегрирование по частям»
Вспомнить формулу 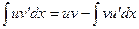 .
.
Задача 291. Вычислить 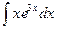 .
.
Решение. Пусть 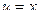 , так надо, чтобы понизилась степень на следующем шаге. Составим таблицу:
, так надо, чтобы понизилась степень на следующем шаге. Составим таблицу:
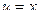
| 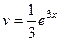
|
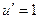
| 
|
Тогда 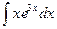 =
= 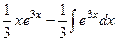 =
= 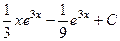 .
.
Ответ. 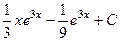 .
.
Задача 292. Вычислить интеграл 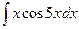 .
.
Решение.
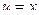
| 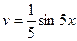
|

| 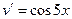
|
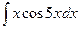 =
= 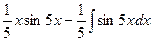 =
= 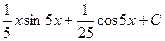 .
.
Ответ. 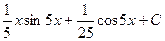 .
.
Задача 293. Вычислить интеграл 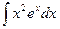 .
.
Решение. Так как степенная функция 2-й степени, то эта задача решается в 2 шага. На первом шаге, обозначаем  ,
, 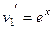 .
.

| 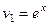
|
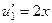
| 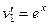
|
Тогда 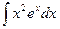 =
= 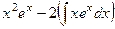 .
.
На 2-м шаге, обозначим  ,
, 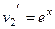 .
.
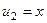
| 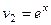
|
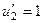
| 
|
В скобке происходит вычисление как бы для нового примера, выполним это вложенное действие:
 =
= 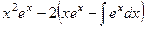 =
= 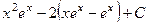 .
.
Ответ. 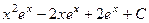 .
.
Задача 294. Вычислить интеграл 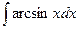
Решение. Пусть  , второго множителя нет, но мы формально можем считать, что он есть, только равен 1. Итак,
, второго множителя нет, но мы формально можем считать, что он есть, только равен 1. Итак,  .
.
Построим таблицу:
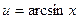
| 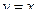
|
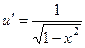
| 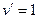
|
Тогда 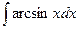 =
= 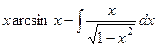 =
=

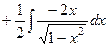 =
= 
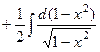 =
=

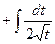 =
= 
 .
.
Ответ. 
 .
.
Задача 295. Вычислить интеграл 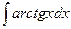
Решение. Производная арктангенса это рациональная дробь. И это мы используем, обозначая её  при интегрировании по частям:
при интегрировании по частям:
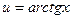
| 
|

| 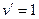
|
Тогда: 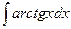 =
= 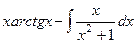 .
.
Второе слагаемое далее уже решается подведением под знак dx.
|
|
 =
= 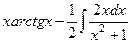 =
=
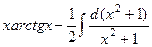 =
=  =
=
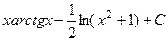 . Знак модуля даже не нужен, т.к.
. Знак модуля даже не нужен, т.к. 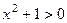 . Ответ.
. Ответ. 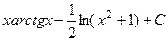 .
.
Задача 296. Вычислить интеграл  .
.
Решение. На этом примере увидим, что иногда полезно отступить от того, что мы, как правило, степенную функцию обозначали через u.
Дело в том, что если так сделать, то при переходе от dv к v возникает интеграл, содержащий первообразную арктангенса 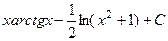 (такую, как в прошлой задаче), что ведёт к сильному усложнению. Напротив, если
(такую, как в прошлой задаче), что ведёт к сильному усложнению. Напротив, если 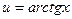 , то его производная состоит только из степенных, то есть происходит значительное упрощение. Конечно же здесь придётся смириться с тем что
, то его производная состоит только из степенных, то есть происходит значительное упрощение. Конечно же здесь придётся смириться с тем что 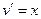 усложняется, растёт его степень, т.е. перейдёт в
усложняется, растёт его степень, т.е. перейдёт в 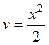 , но зато арктангенс упрощается очень сильно. Итак, построим таблицу:
, но зато арктангенс упрощается очень сильно. Итак, построим таблицу:
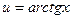
| 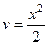
|
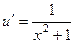
| 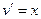
|
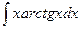 =
=  =
= 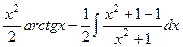 =
=
 =
=  =
=
= 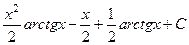 =
= 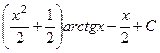 .
.
Ответ. 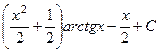 .
.
Домашние задачи.
Д-5. 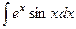 . Ответ.
. Ответ. 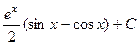
Д-6 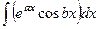 . Ответ.
. Ответ. 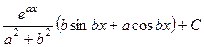 .
.
Решение задачи Д-6: Вычислить 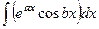 .
.
Решение. На первом шаге,
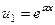
| 
|

| 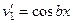
|

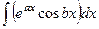 =
= 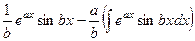 . Теперь в скобках аналогичное выражение, применим к нему такие же преобразования.
. Теперь в скобках аналогичное выражение, применим к нему такие же преобразования.
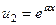
| 
|
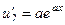
| 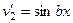
|
Продолжим преобразования:
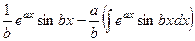 =
=
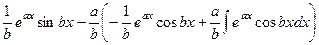 .
.
После двух действий, мы видим снова интеграл 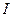 в конце строки.
в конце строки.
Можно записать так, раскрыв скобки:
 . А теперь можно просто выразить это
. А теперь можно просто выразить это 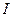 арифметическим путём.
арифметическим путём.
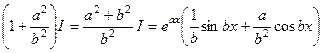
 .
.
|
|
|

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!