Пусть кривая задана формулой 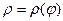 .
.
Тогда:  .
.
Доказательство этой формулы.
Рассмотрим формулы взаимосвязи между полярными и декартовыми координатами:
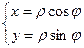
Но в данном случае 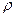 это функция
это функция  . Тогда
. Тогда
 ,
, 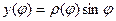 .
.
Здесь параметр 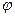 применяется таким же образом, как в прошлой формуле был параметр
применяется таким же образом, как в прошлой формуле был параметр 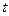 .
.
Найдём производные:
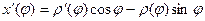
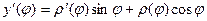
Их надо подставить в формулу: 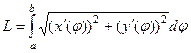 .
.
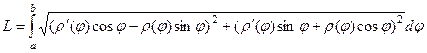
применим формулу сокращённого умножения в каждом квадрате под корнем. Там получатся квадраты и удвоенные произведения, которые, впрочем, сократятся, ведь они будут разного знака. Выражение под корнем преобразуется так:
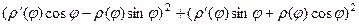 =
=
 +
+
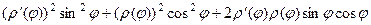 =
=
 =
=
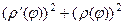 .
.
Поэтому в итоге:  .
.
ПРАКТИКА
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Элементарные преобразования
Задача 268. Вычислить 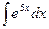 .
.
Решение. Известно, что  . При дифференцровании функций вида
. При дифференцровании функций вида  происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5.
происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5.
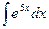 =
= 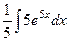 =
= 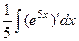 =
= 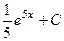 .
.
Ответ. 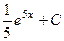 .
.
Задача 269. Вычислить 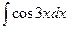 .
.
Решение. Замечая, что 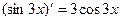 , преобразуем так:
, преобразуем так:
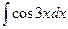 =
= 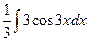 =
= 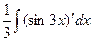 =
= 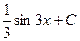 .
.
Ответ. 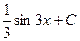 .
.
Задача 270. Вычислить 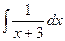 .
.
Решение. Известна формула 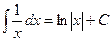 . Если в знаменателе линейная функция вида
. Если в знаменателе линейная функция вида 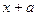 , то можно добавить константу под знаком дифференциала, от этого ничего не изменилось бы, ведь производная константы это 0. Итак,
, то можно добавить константу под знаком дифференциала, от этого ничего не изменилось бы, ведь производная константы это 0. Итак, 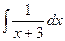 =
=  . Теперь интеграл имеет вид
. Теперь интеграл имеет вид 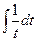 и конечно, равен
и конечно, равен  . Фактически применили замену
. Фактически применили замену 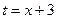 . Сделав обратную замену, получаем ответ:
. Сделав обратную замену, получаем ответ: 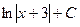 .
.
Ответ. 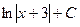 .
.
Задача 271. Вычислить 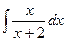 .
.
Решение. Здесь, в отличие от прошлой задачи, уже и в числителе есть переменная, то есть здесь неправильная дробь. Сначала нужно выделить целую часть дроби и отделить правильную дробь. В данном случае для этого достаточно прибавить и отнять 2 в числителе.
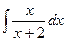 =
= 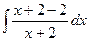 =
= 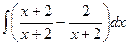 =
= 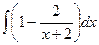 =
=
= 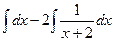 и теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ:
и теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ:  .
.
Ответ. 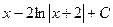 .
.
Задача 272. Вычислить 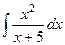 .
.
Решение. В данном случае неправильная дробь, причём степень в числителе более высокая. Можно применить общий метод выделения целой части, то есть поделить числитель на знаменатель.

Получили частное 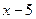 , остаток
, остаток 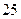 . Теперь можно представить в виде суммы интегралов:
. Теперь можно представить в виде суммы интегралов:
 =
=  =
=  .
.
Впрочем, можно и не делить столбиком, а просто отнять и прибавить 25, тогда  =
= 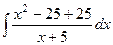 =
= 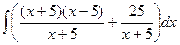 что тоже приводит к
что тоже приводит к 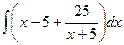 .
.
Теперь, когда свели к сумме табличных интегралов, то с помощью уже ранее изученных действий получаем ответ:
Ответ. 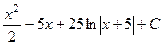 .
.
Задача 273. Вычислить  .
.
Решение. Дискриминант знаменателя отрицательный, поэтому здесь невозможно сделать как в прошлой задаче, так как нет корней знаменателя и дробь невозможно свести к виду 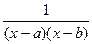 .
.
Но при D < 0 можно выделить полный квадрат:
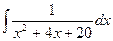 =
= 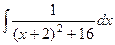 =
= 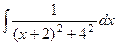 .
.
С помощью замены 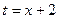 сводится к интегралу:
сводится к интегралу:
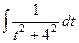 =
= 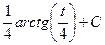 , и далее с помощью обратной замены получаем ответ.
, и далее с помощью обратной замены получаем ответ.
Ответ. 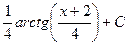 .
.
Задача 274. Вычислить 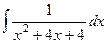 .
.
Решение. В предыдущей задаче было D<0, а в этой D=0.
Выделяя полный квадрат, получим 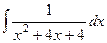 =
=  .
.
В этом случае сводится не к арктангенсу, а к степенной функции, потому что получается 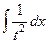 =
=  =
= 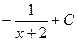 .
.
Ответ. 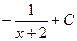 .
.
Задача 275. Доказать формулу 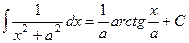 .
.
Решение. Известно, что 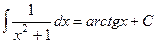 .
.
В выражении 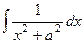 Вынесем за скобку
Вынесем за скобку 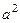 в знаменателе.
в знаменателе.
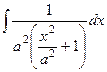 =
= 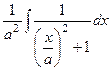 , далее цель - получить
, далее цель - получить  везде, в том числе и под знаком дифференциала, чтобы сделать замену
везде, в том числе и под знаком дифференциала, чтобы сделать замену 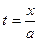 . Домножим и поделим на
. Домножим и поделим на 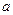 :
:
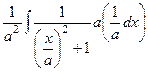 =
=  =
=  =
=
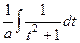 =
= 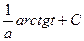 =
=  .
.
Задача 276. Вычислить 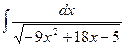 .
.
Решение. 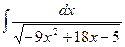 =
= 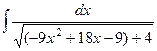 =
=  =
= 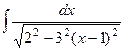 =
= 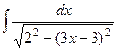 .
.
Для того, чтобы применить формулу, 
нужно обозначить 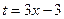 . Но сначала сделаем так, чтобы и в числителе оказался не просто
. Но сначала сделаем так, чтобы и в числителе оказался не просто  а
а 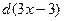 :
:
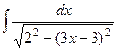 =
=  =
= 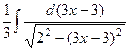 .
.
Теперь интеграл имеет вид  , и равен
, и равен 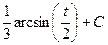 .
.
После обратной замены получаем ответ.
Ответ. 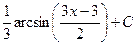 .
.
Кроме различных арифметических преобразований типа разложения многочленов или дробей, существуют задачи, в которых нужно выполнить тригонометрические преобразования подынтегральной функции.
Задача 277. Вычислить интеграл 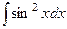 .
.
Решение. Воспользуемся формулой понижения степени, чтобы перейти от степеней тригонометрических функций к выражениям типа 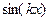 или
или  .
.
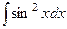 =
=  =
= 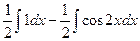 =
= 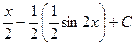 .
.
Ответ.  .
.
Задача 278. Вычислить 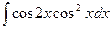 .
.
Решение. Здесь можно было бы применить формулу для косинуса двойного угла, но это преобразование бы только увеличило степени. Поэтому в данном случае для удобнее применить формулу понижения степени ко второму множителю и не менять первый.
 =
=  =
= 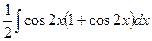 =
=
= 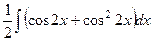 =
= 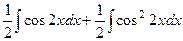 .
.
Первый интеграл вычисляется уже известным способом, а во втором снова понизим степень.
 =
= 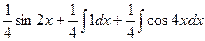 =
= 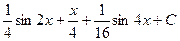 .
.
Ответ. 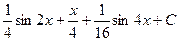 .
.



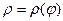 .
. .
.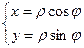
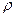 это функция
это функция  . Тогда
. Тогда ,
, 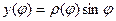 .
.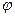 применяется таким же образом, как в прошлой формуле был параметр
применяется таким же образом, как в прошлой формуле был параметр 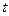 .
.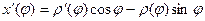
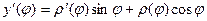
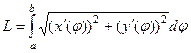 .
.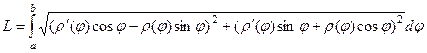
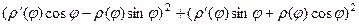 =
= +
+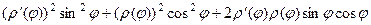 =
= =
=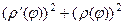 .
. 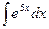 .
. . При дифференцровании функций вида
. При дифференцровании функций вида  происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5.
происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5.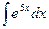 =
= 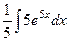 =
= 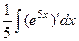 =
= 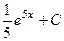 .
. 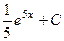 .
.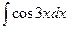 .
.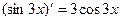 , преобразуем так:
, преобразуем так: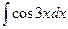 =
= 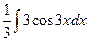 =
= 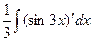 =
= 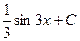 .
.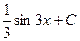 .
.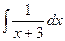 .
. 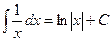 . Если в знаменателе линейная функция вида
. Если в знаменателе линейная функция вида 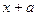 , то можно добавить константу под знаком дифференциала, от этого ничего не изменилось бы, ведь производная константы это 0. Итак,
, то можно добавить константу под знаком дифференциала, от этого ничего не изменилось бы, ведь производная константы это 0. Итак, 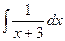 =
=  . Теперь интеграл имеет вид
. Теперь интеграл имеет вид 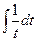 и конечно, равен
и конечно, равен  . Фактически применили замену
. Фактически применили замену 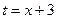 . Сделав обратную замену, получаем ответ:
. Сделав обратную замену, получаем ответ: 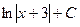 .
.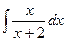 .
. 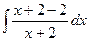 =
= 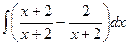 =
= 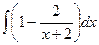 =
=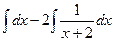 и теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ:
и теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ:  .
.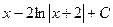 .
.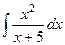 .
.
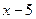 , остаток
, остаток 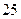 . Теперь можно представить в виде суммы интегралов:
. Теперь можно представить в виде суммы интегралов: =
=  =
=  .
.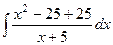 =
= 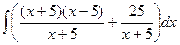 что тоже приводит к
что тоже приводит к 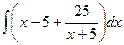 .
.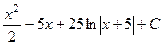 .
. .
.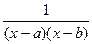 .
.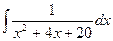 =
= 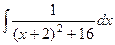 =
= 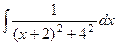 .
.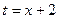 сводится к интегралу:
сводится к интегралу: 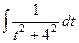 =
= 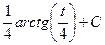 , и далее с помощью обратной замены получаем ответ.
, и далее с помощью обратной замены получаем ответ.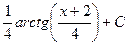 .
.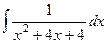 .
.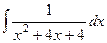 =
=  .
.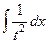 =
=  =
= 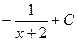 .
.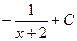 .
.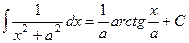 .
. 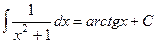 .
.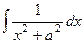 Вынесем за скобку
Вынесем за скобку 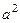 в знаменателе.
в знаменателе.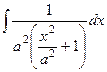 =
= 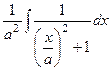 , далее цель - получить
, далее цель - получить  везде, в том числе и под знаком дифференциала, чтобы сделать замену
везде, в том числе и под знаком дифференциала, чтобы сделать замену 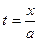 . Домножим и поделим на
. Домножим и поделим на 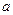 :
: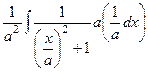 =
=  =
=  =
=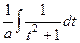 =
= 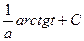 =
=  .
.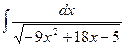 .
.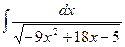 =
= 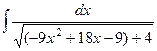 =
=  =
= 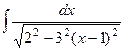 =
= 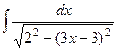 .
.
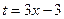 . Но сначала сделаем так, чтобы и в числителе оказался не просто
. Но сначала сделаем так, чтобы и в числителе оказался не просто  а
а 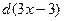 :
: =
= 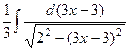 .
. , и равен
, и равен 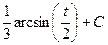 .
.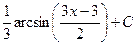 .
.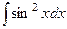 .
.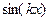 или
или  .
.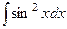 =
=  =
= 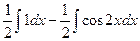 =
= 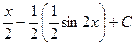 .
. .
.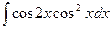 .
. =
=  =
= 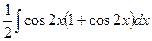 =
=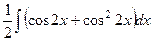 =
= 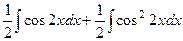 .
. =
= 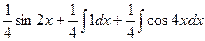 =
= 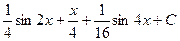 .
.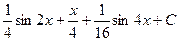 .
.

