Пример: Дана плотность распределения случайной величины X: 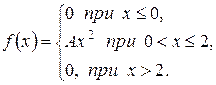
Требуется:
а) найти параметр A;
б) функцию распределения случайной величины X;
в) построить график функции распределения;
г) найти вероятность попадания случайной величины X в интервал 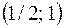 .
.
Решение:
а) Параметр A подберем так, чтобы выполнялось свойство (2) плотности распределения: 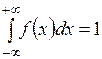 .
.
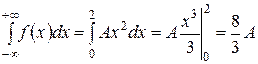 ,
, 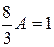 .
.
Отсюда 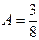 .
.
б) Функцию распределения 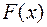 будем искать на каждом интервале отдельно.
будем искать на каждом интервале отдельно.
Для значений 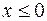
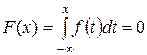 ,
,
Для значений 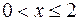
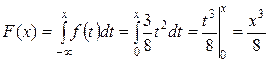 .
.
Для значений 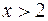
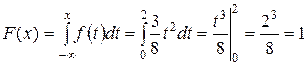 .
.
Таким образом, 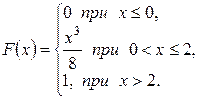
График этой функции изображен на рисунке
в) Вероятность попадания случайной величины X в интервал 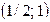 вычисляем по формуле
вычисляем по формуле 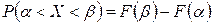 :
:
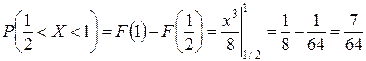 .
.
Контрольные вопросы:
1. Дайте определение НСВ.
2. Плотность и функция распределения.
Задачи на закрепление материала
Дана плотность распределения f (x) случайной величины X. Требуется:
а) найти параметр c;
б) функцию распределения случайной величины X;
в) построить графики функции распределения и плотности распределения;
г) вероятность попадания случайной величины X в интервал 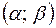 .
.
| 1.
| 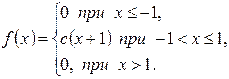 a = 0,1; b = 1,2.
a = 0,1; b = 1,2.
| 2.
| 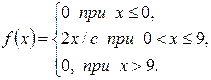 a = 2,5; b = 7,1.
a = 2,5; b = 7,1.
|
3.Задан график плотности распределения с.в. Х
 f(x)
f(x)
 а
а

а х
1) Записать функцию f(x).
2)Найти F (x).
3)Построить графики функций F(x).
4)Вычислить Р(а/2<X<a).
Тема лекции: Числовые характеристики НСВ
Математическое ожидание с.в. Х находится по формул
М(Х)= 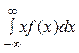 ,
,
если сходится несобственный интеграл.
Дисперсией с.в. Х называют несобственный интеграл
Д(Х)= 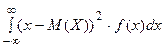 ,
,
если он сходится.
Для вычисления дисперсии более удобна следующая формула:
Д(Х)= 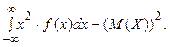
Пример. Случайная величина Х задана плотностью распределения
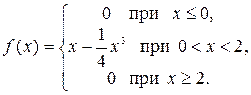
Найти математическое ожидание, дисперсию и среднеквадратичное отклонение с.в. Х.
Воспользуемся определениями.
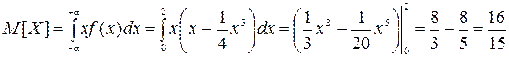 .
.
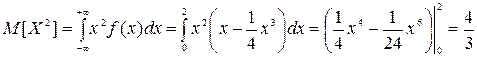 .
.
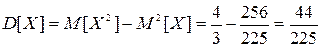 .
.
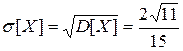 .
.
Пример: Плотность распределения с.в. задана функцией
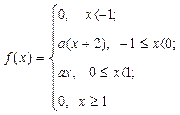
1) Найти а, F(x), М(Х), Д(Х).
2) Вычислить Р(-2<X<1/2).
Решение: Для нахождения параметра а воспользуемся свойством плотности распределения вероятностей: 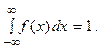
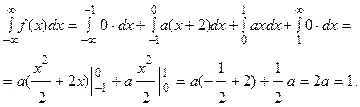 Отсюда находим а=
Отсюда находим а= 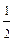 .
.
Тогда функцию плотности распределения можно записать следующим образом:
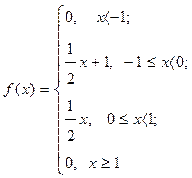
Найдем функцию распределения вероятностей F(x):
Для х<-1 F(x)= 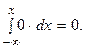
Для -1≤х<0 F(x)= 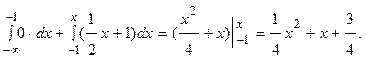
Для 0≤х<1 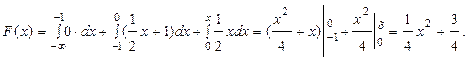
Для х≥1
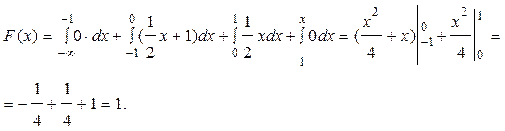
Следовательно, функция распределения имеет вид:
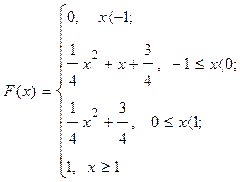
Вычислим числовые характеристики с.в. Х.
Математическое ожидание
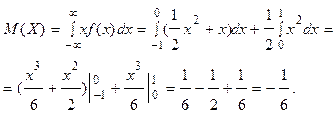
Дисперсия
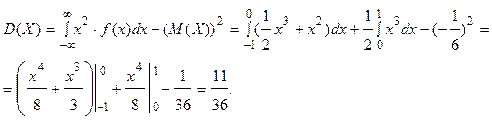
2) Вычислим Р(-2<X<1/2).
Вычислить эту вероятность можно двумя способами: с помощью функции плотности или с помощью функции распределения вероятностей.
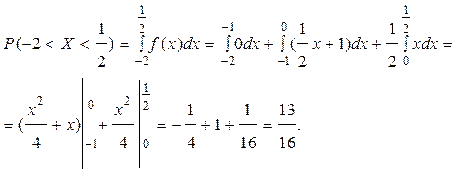
или
Р(-2<X<1/2)=F(1/2)-F(-2)= 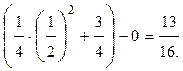
Задачи на закрепление материала
Дана плотность распределения f (x) случайной величины X. Требуется:
а) найти параметр c;
б) функцию распределения случайной величины X;
в) найти числовые характеристики случайной величины X;
г) вероятность попадания случайной величины X в интервал 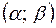 .
.
| 10.
| 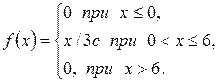 a = 3,2; b = 6,4.
a = 3,2; b = 6,4.
| 20.
| 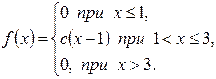 a = 1; b = 2.
a = 1; b = 2.
|
Тема лекции: Основные распределения непрерывных случайных величин
Равномерное распределение
Равномерным называют распределение вероятностей непрерывной случайной величины X, если на отрезке 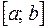 , которому принадлежат все возможные значения X, плотность распределения сохраняет постоянное значение, а именно:
, которому принадлежат все возможные значения X, плотность распределения сохраняет постоянное значение, а именно:
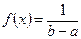 ,
,
вне этого отрезка 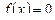 .
.
Математическое ожидание и дисперсия равномерно распределенной случайной величины определяются выражениями:
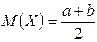 ,
, 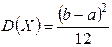 .
.
Показательное распределение
Непрерывная случайная величина X имеет показательное (или экспоненциальное) распределение, если ее плотность распределения имеет вид:
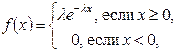
где 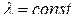 ,
, 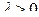 .
.
Числовые характеристики этого распределения определяются равенствами:
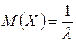 ,
, 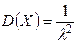 .
.
Нормальное распределение
Непрерывная случайная величина X имеет нормальное распределение (или распределение Гаусса), если ее плотность распределения имеет вид:
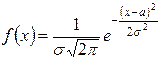 .
.
Постоянные a и s (s > 0) называются параметрами нормального распределения и представляют собой соответственно математическое ожидание и среднеквадратическое отклонение случайной величины X, т. е.
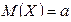 ,
, 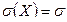 .
.
Отсюда 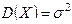 .
.
 График функции
График функции 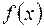 называют нормальной кривой (или кривой Гаусса). Кривая имеет форму «колокола», симметричного относительно прямой
называют нормальной кривой (или кривой Гаусса). Кривая имеет форму «колокола», симметричного относительно прямой 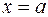 (рис. 1).
(рис. 1).
Функция распределения нормальной случайной величины
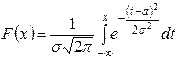
связана с функцией Лапласа соотношением
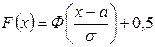 .
.
где 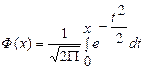 - функция Лапласа, таблицу значений которой можно найти в приложениях.
- функция Лапласа, таблицу значений которой можно найти в приложениях.
Замечание: Ф(х) - функция нечетная, т.е. Ф(-х)=-Ф(х).
Поэтому для нормальной случайной величины справедлива формула
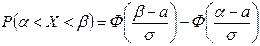 .
.
Вероятность того, что абсолютная величина отклонения нормальной случайной величины меньше положительного чи с ла d, равна:
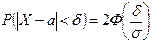 .
.
В частности,
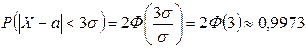 .
.
Отсюда следует «правило трех сигм»: если случайная величина X имеет нормальное распределение, то отклонение этой случайной величины от ее математического ожидания по абсолютной величине не превышает утроенное среднее квадратическое отклонение (3 s).
Нормальный закон – наиболее часто встречающийся закон распределения, он является предельным законом, к которому, при определенных условиях, приближаются другие законы распределения.
Пример. Нормально распределенная случайная величина X задана плотностью вероятности 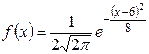 . Требуется найти:
. Требуется найти:
а) математическое ожидание и дисперсию X;
б) вероятность того, что X примет значение, принадлежащее интервалу 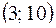 ;
;
в) вероятность того, что абсолютная величина отклонения X от математического ожидания окажется меньше 5.
Решение.
а) Сравнив данную функцию с плотностью нормального распределения, заключаем, что 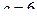 ,
, 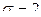 . Следовательно,
. Следовательно, 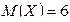 ,
, 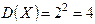 .
.
б) Воспользуемся формулой 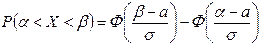 .
.
В нашем случае 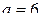 ,
, 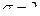 , a = 3; b = 10.
, a = 3; b = 10.
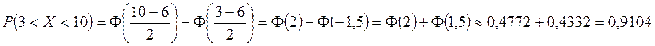 Значения
Значения 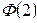 и
и 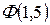 определили по таблице значений функции Лапласа.
определили по таблице значений функции Лапласа.
в) Воспользуемся формулой 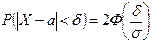 , где
, где 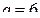 ,
, 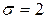 , d = 5.
, d = 5.
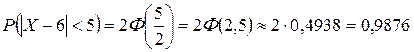 .
.
Пример: Ошибка измерительного прибора - случайная величина, распределенная по нормальному закону, со средним квадратическим отклонением 3 мк. Систематическая ошибка прибора отсутствует. Какова вероятность того, что в независимом измерении ошибка окажется в интервале (0; 2,4)?
Решение: Вычислим вероятность того, что в результате измерения случайная, величина Х - ошибка измерительного прибора будет принадлежать интервалу (0; 2,4):
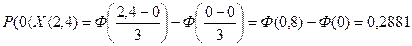
Здесь математическое ожидание a=0 (так как систематическая ошибка отсутствует, то среднее значение ошибки при большом числе измерений будит равно нулю).
Ф(0)=0, Ф(0,8)=0,2881 находим по таблице Лапласа.
Теперь найдем вероятность события 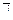 , состоящего в том, что в результате трех измерений
, состоящего в том, что в результате трех измерений
Пример: Случайная величина Х распределена нормально с математическим ожиданием, равным 10. Вероятность того, что случайная величина Х примет значение, принадлежащее интервалу (4; 16), равна 0,8664. Найти среднее квадратическое отклонение этой случайной величины.
Решение: По условию задачи случайная величина Х имеет математическое ожидание а=10 и 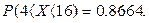
Но, с другой стороны,
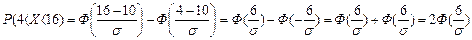
где σ - среднее квадратическое отклонение случайной величины Х.
Итак, 2Ф(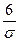 )=0,8664 или Ф(
)=0,8664 или Ф(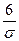 )=0,4332.
)=0,4332.
По таблице значений функции Лапласа находим 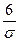 =1,5. Откуда σ=4.
=1,5. Откуда σ=4.
Задачи на закрепление материала
Нормально распределенная случайная величина X задана плотностью вероятности f (x). Требуется найти:
а) математическое ожидание и дисперсию X;
б) вероятность того, что X примет значение, принадлежащее интервалу 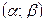 ;
;
в) вероятность того, что абсолютная величина отклонения 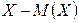 окажется меньше d.
окажется меньше d.
| 1.
| 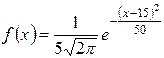 ,
a = 11; b = 21; d = 6. ,
a = 11; b = 21; d = 6.
| 3.
| 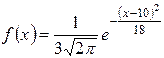 ,
a = 6; b = 15; d = 8. ,
a = 6; b = 15; d = 8.
|
| 2.
| 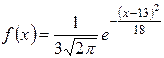 ,
a = 9; b = 19; d = 4. ,
a = 9; b = 19; d = 4.
| 4.
| 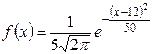 ,
a = 2; b = 15; d = 3. ,
a = 2; b = 15; d = 3.
|
Практические занятия
1. Практическое занятие №2 «Применение стандартных методов и моделей к решению вероятностных задач. Вычисление вероятностей событий по классической формуле определения вероятности»
2. Практическое занятие №3 «Вычисление вероятностей событий, используя теоремы сложения, умножения вероятностей»
3. Практическое занятие №4 «Применение стандартных методов и моделей к решению вероятностных задач. Вычисление вероятностей сложных событий»Практическое занятие №5 «Решение задач на запись ДСВ»
2. Практическое занятие №6 «Вычисление числовых характеристик ДСВ»Практическое занятие №7 «Нахождение интегральной функция распределения НСВ»
2. Практическое занятие №8 «Вычисление характеристик НСВ с помощью функции плотности»
3. Практическое занятие №9 «Вычисление вероятностей для нормального распределения»



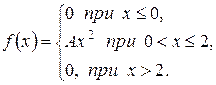
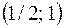 .
.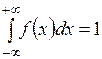 .
.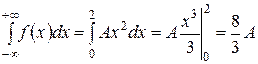 ,
, 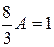 .
.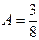 .
.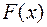 будем искать на каждом интервале отдельно.
будем искать на каждом интервале отдельно.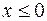
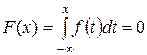 ,
,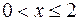
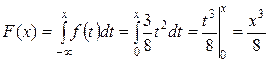 .
.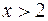
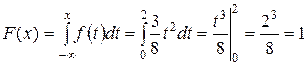 .
.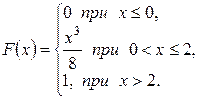

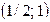 вычисляем по формуле
вычисляем по формуле 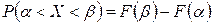 :
: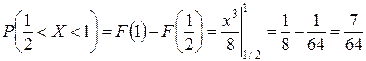 .
.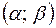 .
.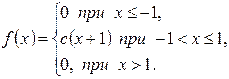 a = 0,1; b = 1,2.
a = 0,1; b = 1,2.
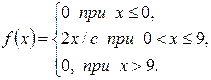 a = 2,5; b = 7,1.
a = 2,5; b = 7,1.
 f(x)
f(x) а
а
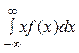 ,
,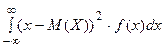 ,
,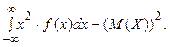
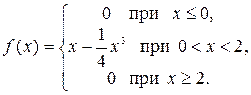
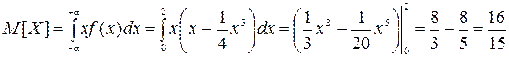 .
.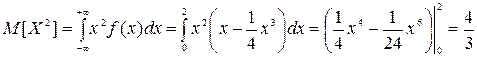 .
.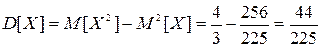 .
.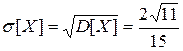 .
.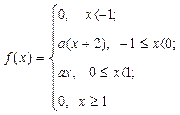
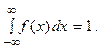
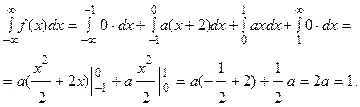 Отсюда находим а=
Отсюда находим а= 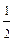 .
.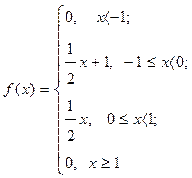
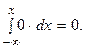
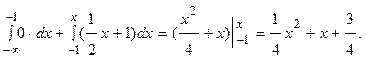
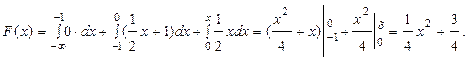
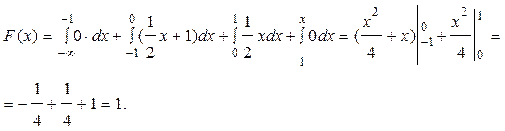
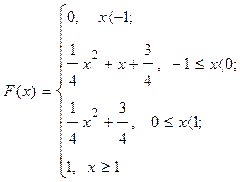
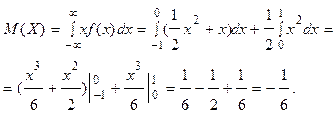
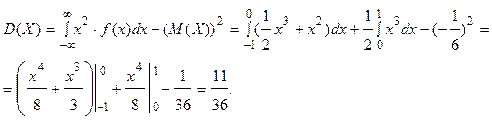
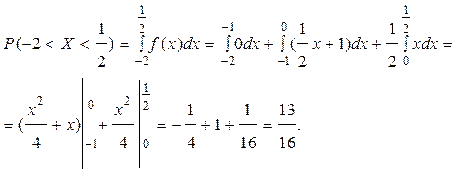
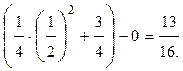
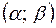 .
.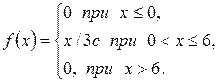 a = 3,2; b = 6,4.
a = 3,2; b = 6,4.
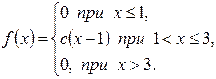 a = 1; b = 2.
a = 1; b = 2.
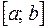 , которому принадлежат все возможные значения X, плотность распределения сохраняет постоянное значение, а именно:
, которому принадлежат все возможные значения X, плотность распределения сохраняет постоянное значение, а именно: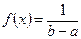 ,
,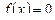 .
.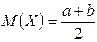 ,
, 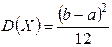 .
.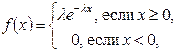
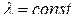 ,
, 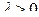 .
.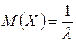 ,
, 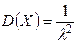 .
.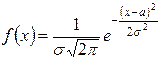 .
.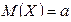 ,
, 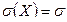 .
.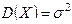 .
. График функции
График функции 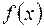 называют нормальной кривой (или кривой Гаусса). Кривая имеет форму «колокола», симметричного относительно прямой
называют нормальной кривой (или кривой Гаусса). Кривая имеет форму «колокола», симметричного относительно прямой 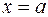 (рис. 1).
(рис. 1).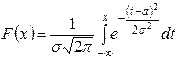
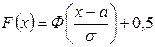 .
.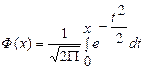 - функция Лапласа, таблицу значений которой можно найти в приложениях.
- функция Лапласа, таблицу значений которой можно найти в приложениях.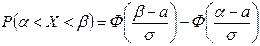 .
.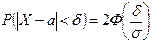 .
.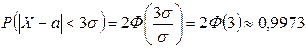 .
.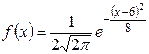 . Требуется найти:
. Требуется найти: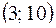 ;
;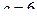 ,
, 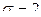 . Следовательно,
. Следовательно, 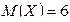 ,
, 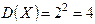 .
.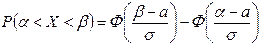 .
.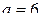 ,
, 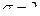 , a = 3; b = 10.
, a = 3; b = 10.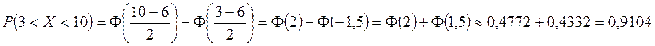 Значения
Значения 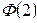 и
и 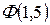 определили по таблице значений функции Лапласа.
определили по таблице значений функции Лапласа.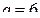 ,
, 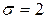 , d = 5.
, d = 5.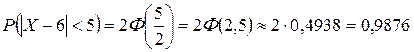 .
.
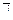 , состоящего в том, что в результате трех измерений
, состоящего в том, что в результате трех измерений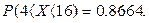
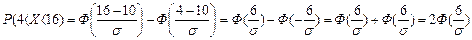
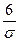 )=0,8664 или Ф(
)=0,8664 или Ф(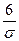 )=0,4332.
)=0,4332.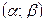 ;
;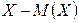 окажется меньше d.
окажется меньше d.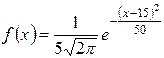 ,
a = 11; b = 21; d = 6.
,
a = 11; b = 21; d = 6.
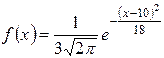 ,
a = 6; b = 15; d = 8.
,
a = 6; b = 15; d = 8.
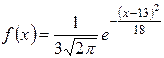 ,
a = 9; b = 19; d = 4.
,
a = 9; b = 19; d = 4.
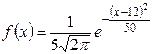 ,
a = 2; b = 15; d = 3.
,
a = 2; b = 15; d = 3.


