Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.
Условия перпендикулярности 2х плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно,  или
или  .
.
Таким образом,  .
.
Условия параллельности 2х плоскостей. Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы 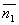 и
и  параллельны, а значит
параллельны, а значит 
Угол между прямыми в пространстве:
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами  и
и  . Так как
. Так как  , то по формуле для косинуса угла между векторами получим
, то по формуле для косинуса угла между векторами получим
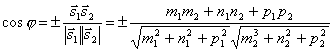 .
.
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов  и
и  :
:
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l 1 параллельна l 2 тогда и только тогда, когда  параллелен
параллелен  .
.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:  .
.
Угол между прямой и плоскостью:
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Вектором называется отрезок, для которого указано, какой из его концов считается началом, а какой - концом. Любая точка пространства рассматривается как нулевой вектор.
 рис. 63 рис. 63
|  - нулевой вектор, обозначается - нулевой вектор, обозначается  . Длина вектора . Длина вектора  обозначается | обозначается |  |. Два ненулевых вектора называются коллинеарными, если они лежат на одной или на параллельных прямых. |. Два ненулевых вектора называются коллинеарными, если они лежат на одной или на параллельных прямых.
|
Пусть два ненулевых вектора  и
и  коллинеарны. Если при этом лучи АВ и СD сонаправлены, то
коллинеарны. Если при этом лучи АВ и СD сонаправлены, то  и
и  называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы
называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы  и
и  называются противоположно направленными.
называются противоположно направленными.
Нулевой вектор условимся считать сонаправленным с любым вектором. Запись 
 означает, что векторы
означает, что векторы  и
и  сонаправлены, а запись
сонаправлены, а запись 
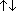
 - что векторы с и d противоположно направлены.
- что векторы с и d противоположно направлены.
 рис. 64 рис. 64
| Векторы называются равными, если они сонаправлены и их длины равны. От любой точки можно отложить вектор, равный данному, и притом только один.
|
Действия над векторами.
1. Сложение векторов по правилу треугольника:

| для этого нужно от произвольной точки пространства отложить вектор  , равный , равный  , затем от точки В отложить вектор , затем от точки В отложить вектор  , равный , равный  . Вектор . Вектор 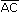 называется суммой называется суммой  и и  . Таким образом . Таким образом  + +  = = 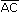 , для любых трех точек А, В и С. , для любых трех точек А, В и С.
|
2.
3. Сложение векторов по правилу параллелограмма:

| для этого векторы откладывают от одной точки.
|
4.
Два ненулевых вектора называются противоположными, если их длины равны и они противоположно направлены.
5. Вычитание векторов:
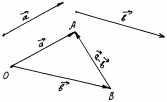 рис. 67 рис. 67
| Разностью векторов  и и  называется такой вектор, сумма которого с вектором называется такой вектор, сумма которого с вектором  равна вектору равна вектору  . Разность . Разность  - -  можно найти по формуле можно найти по формуле  - -  = =  + (- + (-  ), где (- ), где (-  ) - вектор, противоположный вектору ) - вектор, противоположный вектору  . .  - -  = =  . .
|
6.
Сумма нескольких векторов в пространстве вычисляется так же, как и на плоскости и не зависит от порядка слагаемых.
7. Умножение вектора на число. Произведением ненулевого вектора  на число k называется такой вектор
на число k называется такой вектор  , длина которого равна |k|·|
, длина которого равна |k|·|  |, причем векторы
|, причем векторы  и
и  сонаправлены при k
сонаправлены при k  0 и противоположно направлены при k<0. Произведением нулевого вектора на произвольное число считается нулевой вектор.
0 и противоположно направлены при k<0. Произведением нулевого вектора на произвольное число считается нулевой вектор.
Произведение вектора  на число k обозначается так: k
на число k обозначается так: k  . Из определения произведения вектора на число следует, что для любого числа k и любого вектора
. Из определения произведения вектора на число следует, что для любого числа k и любого вектора  векторы
векторы  и k
и k  коллинеарны. Из этого же определения следует, что произведение любого вектора на число нуль есть нулевой вектор.
коллинеарны. Из этого же определения следует, что произведение любого вектора на число нуль есть нулевой вектор.
Для любых векторов  ,
,  и любых чисел k, l справедливы равенства:
и любых чисел k, l справедливы равенства:
(kl)  = k(l
= k(l  ) (сочетательный закон);
) (сочетательный закон);
k( +
+  ) = k
) = k  + k
+ k  (первый распределительный закон);
(первый распределительный закон);
(к+l)  = k
= k  + l
+ l  (второй распределительный закон).
(второй распределительный закон).
Лемма. Если векторы  и
и  коллинеарны и вектор
коллинеарны и вектор  не равен нулевому вектору, то существует число k такое, что вектор
не равен нулевому вектору, то существует число k такое, что вектор  равен k
равен k  .
.
Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости. Ясно, что любые два коллинеарных вектора компланарны; три вектора, среди которых имеется два коллинеарных, также компланарны, а три произвольных вектора могут быть как компланарными, так и некомпланарными.
Если вектор 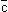 можно представить в виде
можно представить в виде 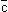 = х
= х  + у
+ у  , где х и у - некоторые числа, то векторы
, где х и у - некоторые числа, то векторы  ,
,  и
и 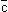 компланарны.
компланарны.
 рис. 68 рис. 68
| Для сложения трёх некомпланарных векторов можно пользоваться так называемым правилом параллелепипеда. Опишем его. Пусть  , ,  , , 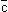 - некомпланарные векторы. Отложим от произвольной точки О пространства векторы - некомпланарные векторы. Отложим от произвольной точки О пространства векторы  = =  , ,  = =  , ,  = = 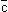 и построим параллелепипед так, чтобы отрезки ОА, ОВ и ОС были рёбрами. Тогда если ОD - диагональ этого параллелепипеда, то и построим параллелепипед так, чтобы отрезки ОА, ОВ и ОС были рёбрами. Тогда если ОD - диагональ этого параллелепипеда, то  = =  + +  + + 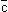 . Действительно, . Действительно,  . .
|
Теорема. Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
Если  ,
,  ,
, 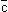 - некомпланарные векторы, то любой вектор
- некомпланарные векторы, то любой вектор  можно представить в виде:
можно представить в виде:
 = х
= х  + у
+ у  + z
+ z 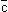 ,
,
где х, у, z - числа.
Основные понятия тригонометрии
В геометрии угол определяется как часть плоскости, ограниченная двумя лучами. При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота. Возьмем на координатной плоскости окружность радиуса R с центром O в начале координат. Пусть одна сторона угла α с вершиной в начале координат O идёт по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс. Из геометрии известно, что отношение длины дуги l, на которую опирается этот угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла:
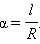
|
Такая мера называется радианной мерой угла и используется наравне с угловой. Говорят, что угол равен определённому числу радиан. Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу. В самом деле:  Обозначение радиана – «рад». Так как длина всей окружности радиуса R равна 2π R, то всей окружности соответствует угол
Обозначение радиана – «рад». Так как длина всей окружности радиуса R равна 2π R, то всей окружности соответствует угол  радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует
радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует 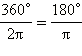 градусов:
градусов:
И наоборот,
Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
и от радианного измерения к градусному:
Обозначение «рад» при записи часто опускают и вместо, например, 180° = π рад пишут просто 180° = π.
Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.
| Угол, градусы
| 0°
| 30°
| 45°
| 60°
| 90°
| 180°
| 270°
| 360°
| | Угол, радианы
| 0
| 
| 
| 
| 
| π
| 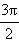
| 2π
| |
| |
Пример 1
Определите радианную меру угла, если его градусная мера равна: 1) 2°; 2) 225°.
Снова рассмотрим на координатной плоскости окружность радиуса R с центром O в начале координат. Как известно, координатные оси делят окружность на четыре дуги, которые называют четвертями.

|
| Рисунок 2.4.1.1.
Окружность радиуса R
|
Рассмотрим произвольный угол α. Изобразим его как угол поворота радиус-вектора 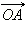 против часовой стрелки. При таком повороте точка A (R; 0) перейдёт в некоторую точку B (x; y) на этой окружности, при этом
против часовой стрелки. При таком повороте точка A (R; 0) перейдёт в некоторую точку B (x; y) на этой окружности, при этом 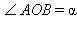 (α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка B, угол α называется углом этой четверти.
(α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка B, угол α называется углом этой четверти.

|
| Рисунок 2.4.1.2
|
Докажем, что отношения  и
и  не зависят от величины радиуса R. Действительно, выберем на отрезке OA точку
не зависят от величины радиуса R. Действительно, выберем на отрезке OA точку 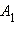 такую, что
такую, что  Построим окружность с центром в начале координат радиуса
Построим окружность с центром в начале координат радиуса  Построенная окружность пересекает радиус-вектор
Построенная окружность пересекает радиус-вектор 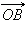 в точке
в точке 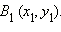 Так как векторы
Так как векторы  и
и  коллинеарны и одинаково направлены, то
коллинеарны и одинаково направлены, то
Однако равные векторы имеют равные координаты, следовательно,
Откуда следует после деления обеих частей последних равенств на R 1, что
Итак, для любого угла поворота отношение координат радиус-вектора к его длине не зависит от этой длины радиус-вектора. Следовательно, отношения  и
и  характеризуют не окружность, а лишь угол поворота. Значит, для того, чтобы рассмотреть основные свойства этих отношений, можно взять окружность любого радиуса, например, R = 1. Так мы и сделаем. Окружность единичного радиуса с центром в начале координат называется тригонометрической окружностью.
характеризуют не окружность, а лишь угол поворота. Значит, для того, чтобы рассмотреть основные свойства этих отношений, можно взять окружность любого радиуса, например, R = 1. Так мы и сделаем. Окружность единичного радиуса с центром в начале координат называется тригонометрической окружностью.

|
| Координатная окружность
|
Ввиду всего вышесказанного, рассмотренные отношения  и пр. как характеристики только угла (но не окружности) удобно как-либо обозначить. Введём несколько ключевых определений.
и пр. как характеристики только угла (но не окружности) удобно как-либо обозначить. Введём несколько ключевых определений.

|
| Функция y = cos x
|

| 
| 
|
|
| Синусом угла α называется ордината y точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.
| 
|

| 
| 
|
|

|
| Функция y = sin x
|

| 
| 
|
|
| Тангенсом угла α называется отношение ординаты y к абсциссе x точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.
| 
|

| 
| 
|
|

|
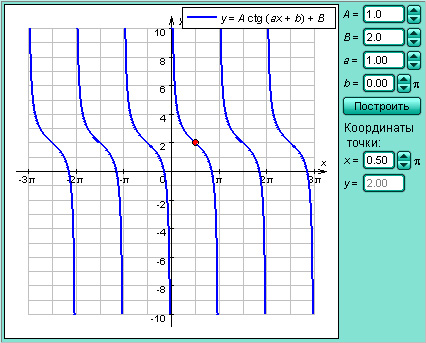
| Модель 2.9. Функция y = tg x
|

| 
| 
|
|
| Котангенсом угла α называется отношение абсциссы x к ординате y точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.
| 
|

| 
| 
|
|
|
| Модель 2.10. Функция y = ctg x
|
Ясно, что для данного угла α функции sin α, cos α, tg α и ctg α, которые называются тригонометрическими функциями, определены однозначно (поскольку каждому углу соответствует единственная точка на тригонометрической окружности). Однако если функции sin α и cos α определены для любого угла α, то функции tg α и ctg α определены только для тех углов, для которых не равен нулю знаменатель дробей  и
и 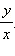 Значит, tg α не определён для углов вида
Значит, tg α не определён для углов вида  где
где 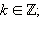 ctg α не определён для углов вида
ctg α не определён для углов вида 
Поскольку синус по определению равен ординате точки на единичной окружности, а косинус − абсциссе, то знаки тригонометрических функций по четвертям будут такими:



 или
или  .
. .
.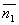 и
и  параллельны, а значит
параллельны, а значит 

 и
и  . Так как
. Так как  , то по формуле для косинуса угла между векторами получим
, то по формуле для косинуса угла между векторами получим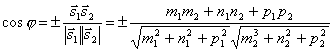 .
. и
и  параллелен
параллелен  .
. .
. рис. 63
рис. 63
 - нулевой вектор, обозначается
- нулевой вектор, обозначается  . Длина вектора
. Длина вектора  обозначается |
обозначается |  коллинеарны. Если при этом лучи АВ и СD сонаправлены, то
коллинеарны. Если при этом лучи АВ и СD сонаправлены, то 
 означает, что векторы
означает, что векторы 
 - что векторы с и d противоположно направлены.
- что векторы с и d противоположно направлены. рис. 64
рис. 64

 , равный
, равный 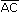 называется суммой
называется суммой 
 рис. 67
рис. 67
 -
-  =
=  .
.
 0 и противоположно направлены при k<0. Произведением нулевого вектора на произвольное число считается нулевой вектор.
0 и противоположно направлены при k<0. Произведением нулевого вектора на произвольное число считается нулевой вектор. рис. 68
рис. 68
 =
=  =
=  .
.
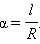
 Обозначение радиана – «рад». Так как длина всей окружности радиуса R равна 2π R, то всей окружности соответствует угол
Обозначение радиана – «рад». Так как длина всей окружности радиуса R равна 2π R, то всей окружности соответствует угол  радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует
радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует 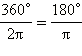 градусов:
градусов:


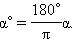




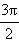

 против часовой стрелки. При таком повороте точка A (R; 0) перейдёт в некоторую точку B (x; y) на этой окружности, при этом
против часовой стрелки. При таком повороте точка A (R; 0) перейдёт в некоторую точку B (x; y) на этой окружности, при этом 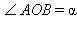 (α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка B, угол α называется углом этой четверти.
(α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка B, угол α называется углом этой четверти.
 и
и  не зависят от величины радиуса R. Действительно, выберем на отрезке OA точку
не зависят от величины радиуса R. Действительно, выберем на отрезке OA точку 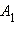 такую, что
такую, что  Построим окружность с центром в начале координат радиуса
Построим окружность с центром в начале координат радиуса  Построенная окружность пересекает радиус-вектор
Построенная окружность пересекает радиус-вектор 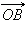 в точке
в точке 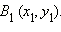 Так как векторы
Так как векторы  коллинеарны и одинаково направлены, то
коллинеарны и одинаково направлены, то














 и
и 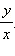 Значит, tg α не определён для углов вида
Значит, tg α не определён для углов вида  где
где 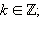 ctg α не определён для углов вида
ctg α не определён для углов вида 



