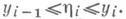Приращение 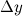 функции
функции  представимо в виде:
представимо в виде:
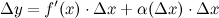
где функция 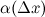 является б.м. функцией при стремлении аргумента
является б.м. функцией при стремлении аргумента 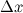 к нулю. Так как
к нулю. Так как 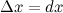 , то
, то
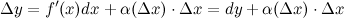
В силу того, что второе слагаемое 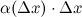 является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому
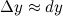
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.
Для приближенного вычисления значения функции применяется следующая формула:
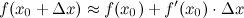
Пример
Задание. Вычислить приближенно 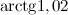 , заменяя приращение функции ее дифференциалом.
, заменяя приращение функции ее дифференциалом.
Решение. Рассмотрим функцию 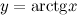 . Необходимо вычислить ее значение в точке
. Необходимо вычислить ее значение в точке 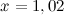 . Представим данное значение в виде следующей суммы:
. Представим данное значение в виде следующей суммы:
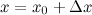
Величины 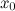 и
и 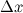 выбираются так, чтобы в точке
выбираются так, чтобы в точке 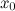 можно было бы достаточно легко вычислить значение функции и ее производной, а
можно было бы достаточно легко вычислить значение функции и ее производной, а 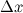 было бы достаточно малой величиной. С учетом этого, делаем вывод, что
было бы достаточно малой величиной. С учетом этого, делаем вывод, что 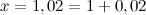 , то есть
, то есть 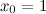 ,
, 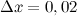 .
.
Вычислим значение функции 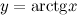 в точке
в точке 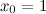 :
:
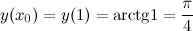
Далее продифференцируем рассматриваемую функцию и найдем значение 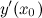 :
:
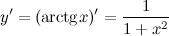
Тогда
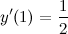
Итак,

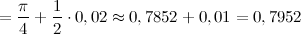
Ответ. 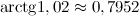
Понятие экстремума функции
Определение
Точка 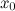 называется точкой локального максимума функции
называется точкой локального максимума функции 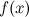 , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех  из этой окрестности выполняется неравенство:
из этой окрестности выполняется неравенство: 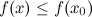 .
.
Точка 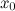 называется точкой локального минимума функции
называется точкой локального минимума функции 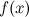 , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех  из этой окрестности
из этой окрестности 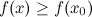 .
.
Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
Точка 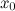 называется точкой строгого локального максимума функции
называется точкой строгого локального максимума функции  , если для всех
, если для всех  из окрестности этой точки будет справедливо строгое неравенство
из окрестности этой точки будет справедливо строгое неравенство 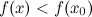 .
.
Точка 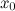 называется точкой строгого локального минимума функции
называется точкой строгого локального минимума функции  , если для всех
, если для всех  из окрестности этой точки будет справедливо строгое неравенство
из окрестности этой точки будет справедливо строгое неравенство 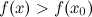 .
.
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
Замечание
Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если функция  имеет экстремум в точке
имеет экстремум в точке 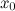 , то ее производная
, то ее производная 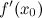 либо равна нулю, либо не существует.
либо равна нулю, либо не существует.
Точки, в которых производная равна нулю: 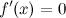 , называются стационарными точками функции.
, называются стационарными точками функции.
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения 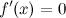 ), либо это точки, в которых производная
), либо это точки, в которых производная 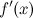 не существует.
не существует.
Замечание
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
Первое достаточное условие экстремума
Теорема
(Первое достаточное условие экстремума)
Пусть для функции  выполнены следующие условия:
выполнены следующие условия:
функция непрерывна в окрестности точки 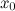 ;
;
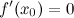 или
или 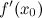 не существует;
не существует;
производная 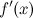 при переходе через точку
при переходе через точку 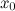 меняет свой знак.
меняет свой знак.
Тогда в точке 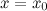 функция
функция  имеет экстремум, причем это минимум, если при переходе через точку
имеет экстремум, причем это минимум, если при переходе через точку 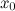 производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку
производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку 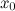 производная меняет свой знак с плюса на минус.
производная меняет свой знак с плюса на минус.
Если производная 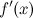 при переходе через точку
при переходе через точку 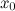 не меняет знак, то экстремума в точке
не меняет знак, то экстремума в точке 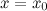 нет.
нет.
Таким образом, для того чтобы исследовать функцию  на экстремум, необходимо:
на экстремум, необходимо:
найти производную 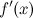 ;
;
найти критические точки, то есть такие значения  , в которых
, в которых 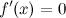 или
или 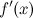 не существует;
не существует;
исследовать знак производной слева и справа от каждой критической точки;
найти значение функции в экстремальных точках.
Пример
Задание. Исследовать функцию 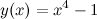 на экстремум.
на экстремум.
Решение. Находим производную заданной функции:
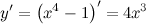
Далее ищем критические точки функции, для этого решаем уравнение 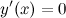 :
:
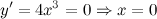
Первая производная определена во всех точках. Таким образом, имеем одну критическую точку 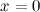 . Наносим эту точку на координатную прямую и исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное значение и находим значение производной в выбранной точке, определяем знак полученной величины):
. Наносим эту точку на координатную прямую и исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное значение и находим значение производной в выбранной точке, определяем знак полученной величины):

Так как при переходе через точку 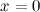 производная сменила свой знак с "-" на "+", то в этой точке функция достигает минимума (или минимального значения), причем
производная сменила свой знак с "-" на "+", то в этой точке функция достигает минимума (или минимального значения), причем 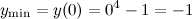 .
.
Замечание. Также можно определить интервалы монотонности функции: так как на интервале 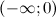 производная
производная 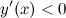 , то на этом интервале функция
, то на этом интервале функция 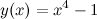 является убывающей; на интервале
является убывающей; на интервале 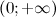 производная
производная 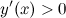 , значит заданная функция возрастает на нем.
, значит заданная функция возрастает на нем.
Ответ. 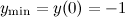
Второе достаточное условие экстремума
Теорема
(Второе достаточное условие экстремума)
Пусть для функции  выполнены следующие условия:
выполнены следующие условия:
она непрерывна в окрестности точки 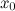 ;
;
первая производная 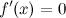 в точке
в точке 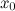 ;
;
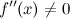 в точке
в точке 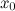 .
.
Тогда в точке 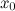 достигается экстремум, причем, если
достигается экстремум, причем, если 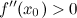 , то в точке
, то в точке 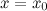 функция
функция  имеет минимум; если
имеет минимум; если 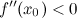 , то в точке
, то в точке 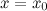 функция
функция  достигает максимум.
достигает максимум.
Пример
Задание. Исследовать функцию 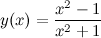 на экстремум с помощью второй производной.
на экстремум с помощью второй производной.
Решение. Находим первую производную заданной функции:
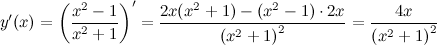
Находим точки, в которых первая производная равна нулю:
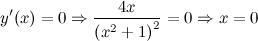
Вторая производная заданной функции:
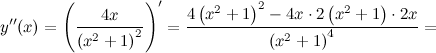
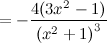
В стационарной точке 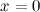 вторая производная
вторая производная 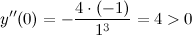 , а значит, в этой точке функция достигает минимум, причем
, а значит, в этой точке функция достигает минимум, причем 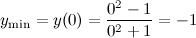 .
.
Ответ. 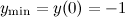
Наибольшее и наименьшее значение функции, непрерывной на отрезке
Если функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке 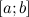 , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение
, то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение 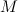 функция
функция 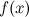 принимает в точке
принимает в точке 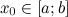 , то
, то 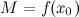 будет локальным максимумом функции
будет локальным максимумом функции 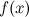 , так как в этом случае существует окрестность точки
, так как в этом случае существует окрестность точки 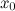 , такая, что
, такая, что 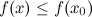 .
.
Однако свое наибольшее значение 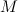 функция
функция 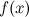 может принимать и на концах отрезка
может принимать и на концах отрезка 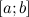 . Поэтому, чтобы найти наибольшее значение
. Поэтому, чтобы найти наибольшее значение 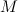 непрерывной на отрезке
непрерывной на отрезке 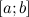 функции
функции 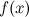 , надо найти все максимумы функции на интервале
, надо найти все максимумы функции на интервале 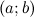 и значения
и значения 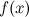 на концах отрезка
на концах отрезка 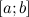 , то есть
, то есть 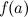 и
и 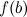 , и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.
, и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.
Наименьшим значением 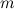 непрерывной на отрезке
непрерывной на отрезке 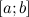 функции
функции 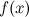 будет наименьший минимум среди всех минимумов функции
будет наименьший минимум среди всех минимумов функции 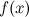 на интервале
на интервале 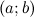 и значений
и значений 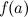 и
и 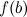 .
.
Пример
Задание. Найти наибольшее и наименьшее значение функции 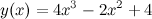 на отрезке
на отрезке 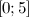 .
.
Решение. Находим производную функции:
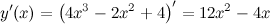
Находим точки, в которых производная равна нулю:
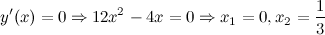
Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку 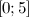 . Оба значения лежат в этом промежутке.
. Оба значения лежат в этом промежутке.
Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:
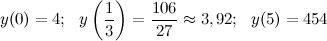
Таким образом,
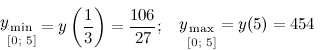
Ответ. 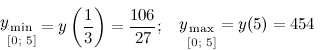
Выпуклость функции, точки перегиба
График функции  , дифференцируемой на интервале
, дифференцируемой на интервале 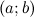 , является на этом интервале выпуклым, если график этой функции в пределах интервала
, является на этом интервале выпуклым, если график этой функции в пределах интервала 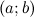 лежит не выше любой своей касательной (рис. 1).
лежит не выше любой своей касательной (рис. 1).
График функции  , дифференцируемой на интервале
, дифференцируемой на интервале 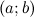 , является на этом интервале вогнутым, если график этой функции в пределах интервала
, является на этом интервале вогнутым, если график этой функции в пределах интервала 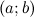 лежит не ниже любой своей касательной (рис. 2).
лежит не ниже любой своей касательной (рис. 2).

Теоремы о выпуклости функции и точках перегиба
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть функция  определена на интервале
определена на интервале 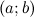 и имеет непрерывную, не равную нулю в точке
и имеет непрерывную, не равную нулю в точке 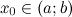 вторую производную. Тогда, если
вторую производную. Тогда, если 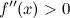 всюду на интервале
всюду на интервале 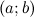 , то функция имеет вогнутость на этом интервале, если
, то функция имеет вогнутость на этом интервале, если 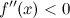 , то функция имеет выпуклость.
, то функция имеет выпуклость.
Определение
Точкой перегиба графика функции  называется точка
называется точка 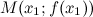 , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если функция  имеет перегиб в точке
имеет перегиб в точке 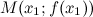 , то
, то 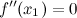 или не существует.
или не существует.
Теорема
(О достаточном условии существования точки перегиба)
Если:
первая производная 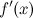 непрерывна в окрестности точки
непрерывна в окрестности точки 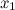 ;
;
вторая производная 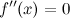 или не существует в точке
или не существует в точке 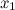 ;
;
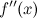 при переходе через точку
при переходе через точку 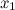 меняет свой знак,
меняет свой знак,
тогда в точке 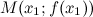 функция
функция  имеет перегиб.
имеет перегиб.
Схема исследования функции на выпуклость, вогнутость
Найти вторую производную функции.
Найти точки, в которых вторая производная равна нулю или не существует.
Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.
Пример
Задание. Найти интервалы выпуклости/вогнутости функции 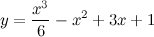
Решение. Найдем вторую производную заданной функции:
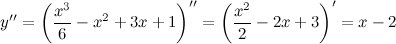
Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение 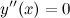 :
:
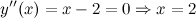
Исследуем знак второй производной слева и справа от полученной точки:
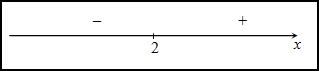
Так как на промежутке 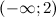 вторая производная
вторая производная 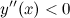 , то на этом промежутке функция
, то на этом промежутке функция 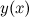 выпукла; в силу того, что на промежутке
выпукла; в силу того, что на промежутке 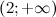 вторая производная
вторая производная 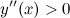 - функция вогнута. Так как при переходе через точку
- функция вогнута. Так как при переходе через точку 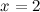 вторая производная сменила знак, то эта точка является точкой перегиба графика функции.
вторая производная сменила знак, то эта точка является точкой перегиба графика функции.
Ответ. Точка 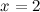 - точка перегиба графика функции.
- точка перегиба графика функции.
На промежутке 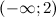 функция выпукла, на промежутке
функция выпукла, на промежутке 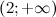 функция вогнута.
функция вогнута.
Асимптоты графика функции
Виды асимптот
Определение
Прямая 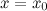 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений 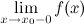 или
или 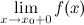 равно
равно 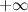 или
или 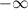 .
.
Замечание. Прямая 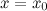 не может быть вертикальной асимптотой, если функция непрерывна в точке
не может быть вертикальной асимптотой, если функция непрерывна в точке 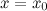 . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
. Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Определение
Прямая 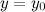 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции  , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений 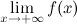 или
или 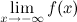 равно
равно 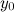 .
.
Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
Определение
Прямая 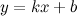 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции  , если
, если 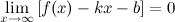
Нахождение наклонной асимптоты
Теорема
(условиях существования наклонной асимптоты)
Если для функции  существуют пределы
существуют пределы 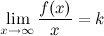 и
и  , то функция имеет наклонную асимптоту
, то функция имеет наклонную асимптоту 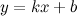 при
при 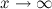 .
.
Замечание
Горизонтальная асимптота является частным случаем наклонной при 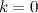 .
.
Замечание
Если при нахождении горизонтальной асимптоты получается, что 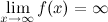 , то функция может иметь наклонную асимптоту.
, то функция может иметь наклонную асимптоту.
Замечание
Кривая  может пересекать свою асимптоту, причем неоднократно.
может пересекать свою асимптоту, причем неоднократно.
Пример
Задание. Найти асимптоты графика функции 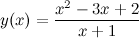
Решение. Область определения функции:
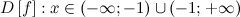
а) вертикальные асимптоты: прямая 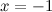 - вертикальная асимптота, так как
- вертикальная асимптота, так как
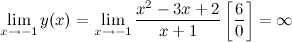
б) горизонтальные асимптоты: находим предел функции на бесконечности:
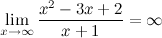
то есть, горизонтальных асимптот нет.
в) наклонные асимптоты 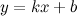 :
:
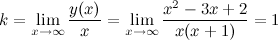
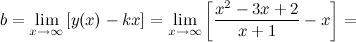
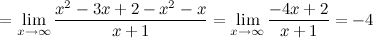
Таким образом, наклонная асимптота: 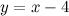 .
.
Ответ. Вертикальная асимптота - прямая 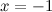 .
.
Наклонная асимптота - прямая 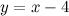 .
.
Исследование функции и построение ее графика
При построении графика функции необходимо провести ее предварительное исследование. Примерная схема исследования функции с целью построения ее графика имеет следующую структуру:
Область определения 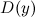 и область допустимых значений
и область допустимых значений 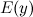 функции.
функции.
Четность, нечетность функции.
Точки пересечения с осями.
Асимптоты функции.
Экстремумы и интервалы монотонности.
Точки перегиба и промежутки выпуклости, вогнутости.
Сводная таблица.
Замечание
Схема представлена как примерная. Пункты исследования можно опускать, если они дают банальную информацию, или переставлять, если обнаруживаются интересные особенности поведения графика.
Замечание
Для уточнения графика можно найти некоторые дополнительные точки, но иногда удается обойтись и без них.
Замечание
Рекомендуется строить график одновременно с исследованием функции, нанося на координатную плоскость информацию по завершении каждого пункта исследования.
Пример
Задание. Исследовать функцию 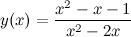 и построить ее график.
и построить ее график.
Решение. 1) Область определения функции.
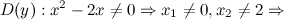
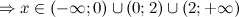
2) Четность, нечетность.
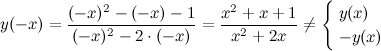
Функция общего вида.
3) Точки пересечения с осями.
а) с осью 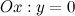 :
:
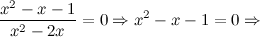
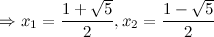
то есть точки 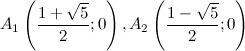
б) с осью 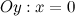 : в данной точке функция неопределенна.
: в данной точке функция неопределенна.
4) Асимптоты.
а) вертикальные: прямые 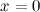 и
и 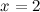 - вертикальные асимптоты.
- вертикальные асимптоты.
б) горизонтальные асимптоты:
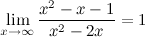
то есть прямая 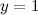 - горизонтальная асимптота.
- горизонтальная асимптота.
в) наклонные асимптоты 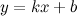 :
:
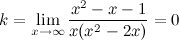
Таким образом, наклонных асимптот нет.
5) Критические точки функции, интервалы возрастания, убывания.
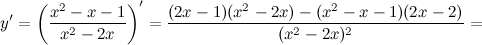
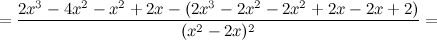
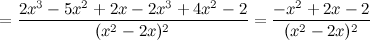
Найдем точки, в которых первая производная равна нулю или не существует: 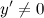 для любого
для любого  из области определения функции;
из области определения функции; 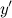 не существует при
не существует при 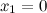 и
и 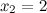 .
.

Таким образом, функция убывает на всей области существования. Точек экстремума нет.
6) Точки перегиба, интервалы выпуклости, вогнутости.
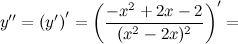
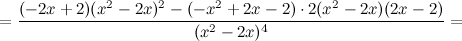
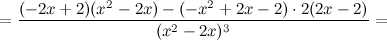
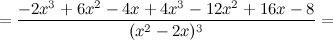
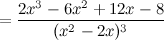
Найдем точки, в которых вторая производная равна нулю или не существует: 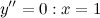 ; при
; при 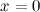 и
и 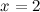 вторая производная не существует.
вторая производная не существует.
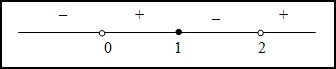
Таким образом, на промежутках 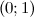 и
и 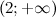 функция вогнута, а на промежутках
функция вогнута, а на промежутках 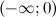 и
и 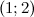 - выпукла. Так как при переходе через точку
- выпукла. Так как при переходе через точку 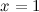 вторая производная поменяла знак, то эта точка является точкой перегиба.
вторая производная поменяла знак, то эта точка является точкой перегиба.
7) Эскиз графика.
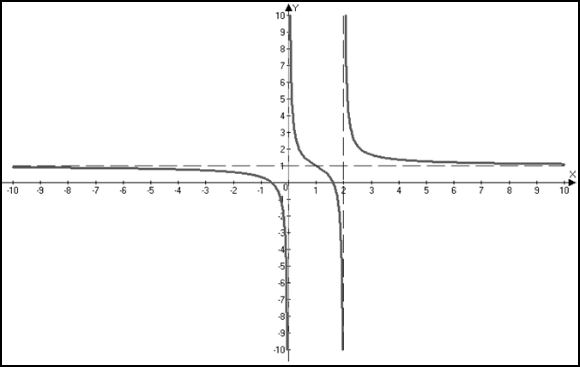
ИНТЕГРАЛ
Неопределенный интеграл.
Первообразной функции f (х)одного переменного хна интервале а<х<b наз. любая функция F(x), производная к-рой для любого хиз этого интервала равна f(x). Очевидно, что если F(x)является первообразной функции f(x)нa интервале а<x<b, то и функция F1 (х) = F (x) +C, где С- любая постоянная, также является первообразной f(x)на этом интервале. Верно и обратное: любые две первообразные одной и той же функции f(x)на интервале a<x<b могут отличаться лишь на постоянную. Следовательно, если F(x)- одна из первообразных f(x)на интервале a<x<b, то любая первообразная f(x)на этом интервале имеет вид F(x) +C, где С- постоянная. Совокупность всех первообразных функции f (х)на интервале a<x<b наз. неопределенным интегралом функции f(x)(на этом интервале) и обозначается символом
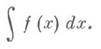
Согласно основной теореме интегрального исчисления, для каждой непрерывной на интервале a<x<b функции f(х)существует на этом интервале первообразная и, следовательно, неопределенный И.
- одно из центральных понятий математич. анализа и всей математики, возникновение к-рого связано с двумя задачами: о восстановлении функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по известной скорости этой точки); о вычислении площади, заключенной между графиком функции f(x)на отрезке 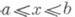 и осью абсцисс (к этой же задаче приводит вычисление работы, произведенной силой за промежуток времени
и осью абсцисс (к этой же задаче приводит вычисление работы, произведенной силой за промежуток времени 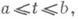 и другие вопросы).
и другие вопросы).
Указанные две задачи приводят к двум видам И.: неопределенному и определенному. Изучение свойств и вычисление этих связанных между собой видов И. составляет задачу интегрального исчисления.
В ходе развития математики и под влиянием потребностей естествознания и техники понятия неопределенного и определенного И. подвергались ряду обобщений и изменений.
Таблица интегралов, таблица неопределенных интегралов
Основные формулы

Определенный интеграл.
Понятие определенного И. вводится либо как предел интегральных сумм (см. Ноши интеграл, Римана интеграл, Лебега интеграл, Колмогорова интеграл, Стилтьеса интеграл), либо в случае, когда заданная функция f(x)определена на нек-ром отрезке [ а, b ]и имеет на нем первообразную F, как разность ее значений на концах рассматриваемого отрезка F(b) - F (a). Определенный И. от функции f(x)на отрезке [ а, b ] обозначают 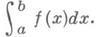 Определение И. как предела интегральных сумм в случае непрерывных функций было сформулировано О. Коши (А. Саuchy) в 1823. Случай произвольных функций был изучен Б. Риманом (В. Riemann, 1853). Существенное продвижение в теории определенного И. принадлежит Г. Дарбу (G. Darboux, 1879), к-рый ввел в рассмотрение наряду с интегральной суммой Римана верхнюю и нижнюю суммы (см. Дарбу сумма). Необходимое и достаточное условие интегрируемости по Риману разрывных функций в законченной форме установил (1902) А. Лебег (Н. Lebesgue).
Определение И. как предела интегральных сумм в случае непрерывных функций было сформулировано О. Коши (А. Саuchy) в 1823. Случай произвольных функций был изучен Б. Риманом (В. Riemann, 1853). Существенное продвижение в теории определенного И. принадлежит Г. Дарбу (G. Darboux, 1879), к-рый ввел в рассмотрение наряду с интегральной суммой Римана верхнюю и нижнюю суммы (см. Дарбу сумма). Необходимое и достаточное условие интегрируемости по Риману разрывных функций в законченной форме установил (1902) А. Лебег (Н. Lebesgue).
Между определенным И. от непрерывной на отрезке [а, b]функции f(x)и неопределенным И. (или первообразной) этой функции существует следующая связь:
1) если F(x)- любая первообразная функции f(x), то справедлива формула Ньютона - Лейбница
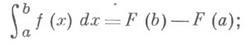
2) для любого х из отрезка [ а, b ] неопределенный И. непрерывной функции f(х)записывается в виде
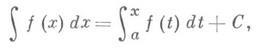
где С- произвольная постоянная. В частности, определенный И. с переменным верхним пределом
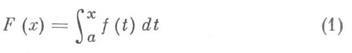
представляет собой первообразную функцию f(х). Для введения определенного И. от функции f(x)по отрезку [ а, b ]в смысле Лебега разбивают множество значений уна частичные отрезки точками...<y_2<у -1 <y 0 <у 1 <у 2 <... и обозначают через М i множество всех значений хиз отрезка [ а, b ], для к-рых yi-1 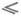 f(x)< yi, а через m(М i) - меру множества М i в смысле Лебега. Интегральную сумму Лебега функции f(x)на отрезке [ а, b ] определяют равенством
f(x)< yi, а через m(М i) - меру множества М i в смысле Лебега. Интегральную сумму Лебега функции f(x)на отрезке [ а, b ] определяют равенством

где hi - любое число из отрезка 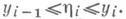



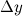 функции
функции  представимо в виде:
представимо в виде: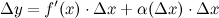
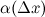 является б.м. функцией при стремлении аргумента
является б.м. функцией при стремлении аргумента 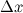 к нулю. Так как
к нулю. Так как 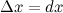 , то
, то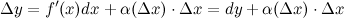
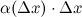 является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому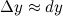
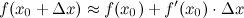
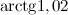 , заменяя приращение функции ее дифференциалом.
, заменяя приращение функции ее дифференциалом.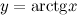 . Необходимо вычислить ее значение в точке
. Необходимо вычислить ее значение в точке 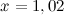 . Представим данное значение в виде следующей суммы:
. Представим данное значение в виде следующей суммы: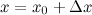
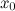 и
и 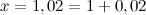 , то есть
, то есть 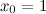 ,
, 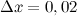 .
.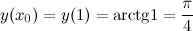
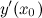 :
: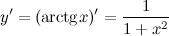
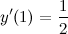

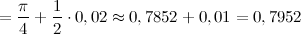
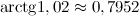
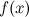 , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех  из этой окрестности выполняется неравенство:
из этой окрестности выполняется неравенство: 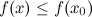 .
.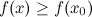 .
.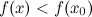 .
.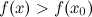 .
.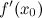 либо равна нулю, либо не существует.
либо равна нулю, либо не существует.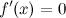 , называются стационарными точками функции.
, называются стационарными точками функции.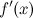 не существует.
не существует.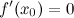 или
или 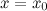 функция
функция 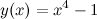 на экстремум.
на экстремум.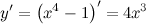
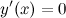 :
: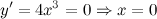
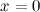 . Наносим эту точку на координатную прямую и исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное значение и находим значение производной в выбранной точке, определяем знак полученной величины):
. Наносим эту точку на координатную прямую и исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное значение и находим значение производной в выбранной точке, определяем знак полученной величины):
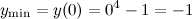 .
.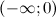 производная
производная 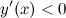 , то на этом интервале функция
, то на этом интервале функция 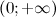 производная
производная 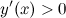 , значит заданная функция возрастает на нем.
, значит заданная функция возрастает на нем.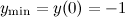
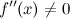 в точке
в точке 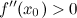 , то в точке
, то в точке 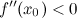 , то в точке
, то в точке 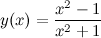 на экстремум с помощью второй производной.
на экстремум с помощью второй производной.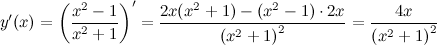
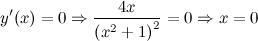
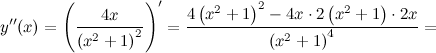
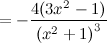
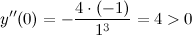 , а значит, в этой точке функция достигает минимум, причем
, а значит, в этой точке функция достигает минимум, причем 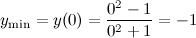 .
.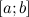 , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение
, то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение 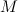 функция
функция 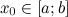 , то
, то 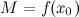 будет локальным максимумом функции
будет локальным максимумом функции 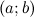 и значения
и значения 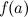 и
и 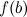 , и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.
, и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.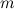 непрерывной на отрезке
непрерывной на отрезке 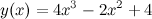 на отрезке
на отрезке 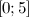 .
.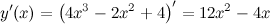
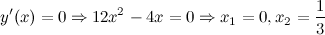
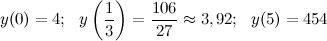
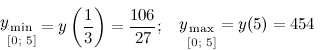

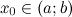 вторую производную. Тогда, если
вторую производную. Тогда, если 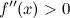 всюду на интервале
всюду на интервале 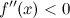 , то функция имеет выпуклость.
, то функция имеет выпуклость.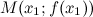 , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости.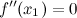 или не существует.
или не существует.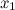 ;
;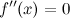 или не существует в точке
или не существует в точке 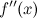 при переходе через точку
при переходе через точку 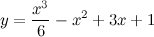
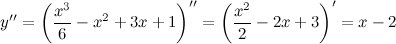
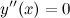 :
: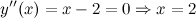

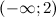 вторая производная
вторая производная 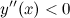 , то на этом промежутке функция
, то на этом промежутке функция 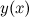 выпукла; в силу того, что на промежутке
выпукла; в силу того, что на промежутке 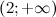 вторая производная
вторая производная 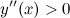 - функция вогнута. Так как при переходе через точку
- функция вогнута. Так как при переходе через точку 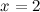 вторая производная сменила знак, то эта точка является точкой перегиба графика функции.
вторая производная сменила знак, то эта точка является точкой перегиба графика функции.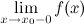 или
или 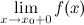 равно
равно 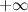 или
или 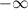 .
.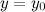 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 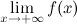 или
или 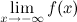 равно
равно 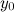 .
.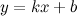 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 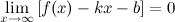
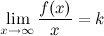 и
и  , то функция имеет наклонную асимптоту
, то функция имеет наклонную асимптоту 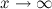 .
.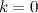 .
.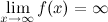 , то функция может иметь наклонную асимптоту.
, то функция может иметь наклонную асимптоту.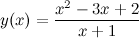
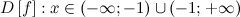
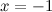 - вертикальная асимптота, так как
- вертикальная асимптота, так как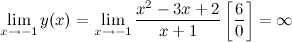
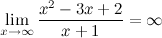
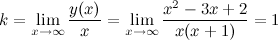
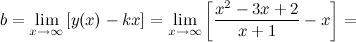
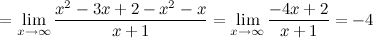
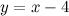 .
.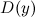 и область допустимых значений
и область допустимых значений 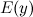 функции.
функции.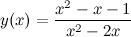 и построить ее график.
и построить ее график.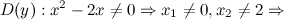
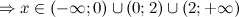
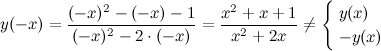
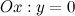 :
: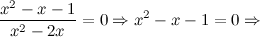
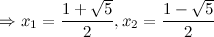
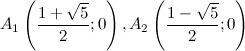
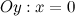 : в данной точке функция неопределенна.
: в данной точке функция неопределенна.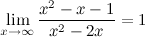
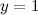 - горизонтальная асимптота.
- горизонтальная асимптота.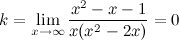
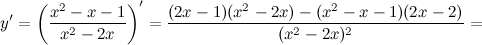
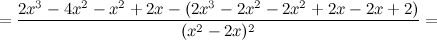
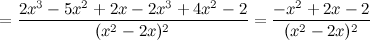
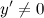 для любого
для любого 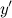 не существует при
не существует при 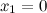 и
и 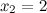 .
.
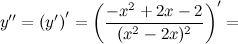
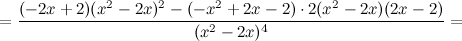
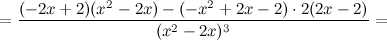
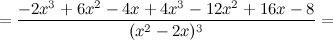
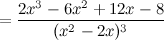
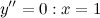 ; при
; при 
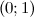 и
и 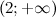 функция вогнута, а на промежутках
функция вогнута, а на промежутках 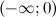 и
и 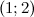 - выпукла. Так как при переходе через точку
- выпукла. Так как при переходе через точку 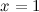 вторая производная поменяла знак, то эта точка является точкой перегиба.
вторая производная поменяла знак, то эта точка является точкой перегиба.
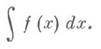
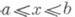 и осью абсцисс (к этой же задаче приводит вычисление работы, произведенной силой за промежуток времени
и осью абсцисс (к этой же задаче приводит вычисление работы, произведенной силой за промежуток времени 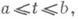 и другие вопросы).
и другие вопросы).
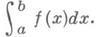 Определение И. как предела интегральных сумм в случае непрерывных функций было сформулировано О. Коши (А. Саuchy) в 1823. Случай произвольных функций был изучен Б. Риманом (В. Riemann, 1853). Существенное продвижение в теории определенного И. принадлежит Г. Дарбу (G. Darboux, 1879), к-рый ввел в рассмотрение наряду с интегральной суммой Римана верхнюю и нижнюю суммы (см. Дарбу сумма). Необходимое и достаточное условие интегрируемости по Риману разрывных функций в законченной форме установил (1902) А. Лебег (Н. Lebesgue).
Определение И. как предела интегральных сумм в случае непрерывных функций было сформулировано О. Коши (А. Саuchy) в 1823. Случай произвольных функций был изучен Б. Риманом (В. Riemann, 1853). Существенное продвижение в теории определенного И. принадлежит Г. Дарбу (G. Darboux, 1879), к-рый ввел в рассмотрение наряду с интегральной суммой Римана верхнюю и нижнюю суммы (см. Дарбу сумма). Необходимое и достаточное условие интегрируемости по Риману разрывных функций в законченной форме установил (1902) А. Лебег (Н. Lebesgue).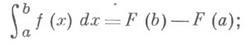
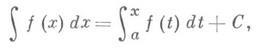
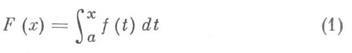
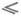 f(x)< yi, а через m(М i) - меру множества М i в смысле Лебега. Интегральную сумму Лебега функции f(x)на отрезке [ а, b ] определяют равенством
f(x)< yi, а через m(М i) - меру множества М i в смысле Лебега. Интегральную сумму Лебега функции f(x)на отрезке [ а, b ] определяют равенством