
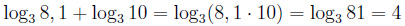
Логарифм частного — это разность логарифмов
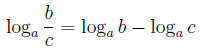
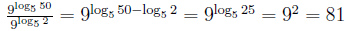
Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа 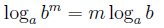
Показатель степени основания логарифма 
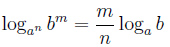 , в частности если m = n, мы получаем формулу:
, в частности если m = n, мы получаем формулу:  , например:
, например: 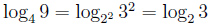
Переход к новому основанию
 , частности, если c = b, то
, частности, если c = b, то 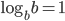 , и тогда:
, и тогда:
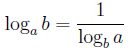
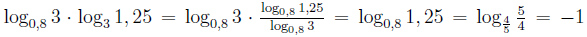
Показательная функция
Ключевые слова: функция, показательная функция, график, степень, основание степени
При a > 0, a ≠≠ 1, определена функция y = a x , отличная от постоянной. Эта функция называется показательной функцией с основанием a.
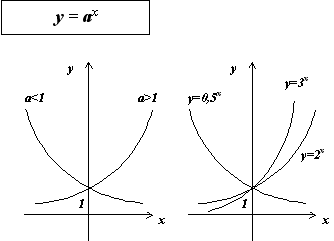
Основные свойства показательной функции y = a x при a > 1:
- Область определения функции - вся числовая прямая.
- Область значений функции - промежуток (0;+∞)(0;+∞).
- Функция строго монотонно возрастает на всей числовой прямой, то есть, если x 1 < x 2, то ax 1 < ax 2.
- При x = 0 значение функции равно 1.
- Если x > 0, то a x > 1 и если x < 0, то 0 < a < 1.
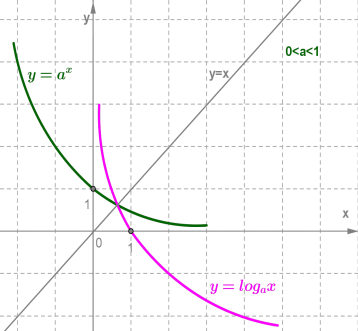
Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на рисунке.
Основные свойства показательной функции y = a x при 0 < a < 1:
- Область определения функции - вся числовая прямая.
- Область значений функции - промежуток (0;+∞)(0;+∞).
- Функция строго монотонно возрастает на всей числовой прямой, то есть, если x 1 < x 2, то ax 1 > ax 2.
- При x = 0 значение функции равно 1.
- Если x > 0, то 0 < a < 1 и если x < 0, то a x > 1.
К общим свойствам показательной функции как при 0 < a < 1, так и при a > 1 относятся:
- ax 1 ax 2 = ax 1+ x 2, для всех x 1и x 2.
- a−x=(ax)−1=1axa−x=(ax)−1=1ax для любого x.
- n√ax=axnaxn=axn для любого x и любого n∈N,n≠1n∈N,n≠1.
- (ab) x = ax bx для любых a, b > 0; a,b ≠1≠1.
- (ab)x=axbx(ab)x=axbx для любых a, b > 0; a,b ≠1≠1.
- ax 1 = ax 2, то x 1= x 2.
Логарифмическая функция, ее свойства и график
Теория:
Функцию, заданную формулой y=logax, называют логарифмической функцией с основанием a.
(a>0,a≠1)

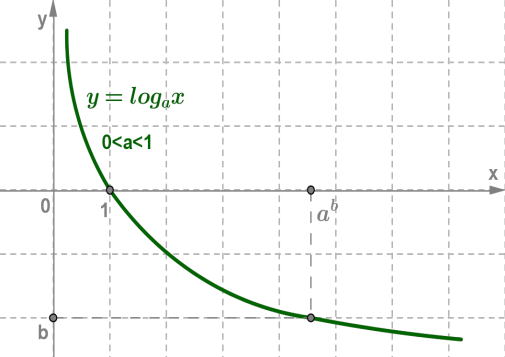
Основные свойства логарифмической функции:
1. Область определения логарифмической функции - множество всех положительных чисел.
D(f)=(0;+∞);
2. Множество значений логарифмической функции - множество R всех действительных чисел.
E(f)=(−∞;+∞);
3. Логарифмическая функция на всей области определения возрастает при a>1 или убывает
при 0<a<1.
Обрати внимание!
Логарифмическая функция не является ни четной, ни нечетной;
не имеет ни наибольшего, ни наименьшего значений;
не ограничена сверху, не ограничена снизу;
График любой логарифмической функции y=logax проходит через точку (1;0).
Построим графики двух функций
Пример:
1. y=log2x, основание 2>1
| x
| 14
| 12
| 1
| 2
| 4
| 8
|
| y=log2x
| −2
| −1
| 0
| 1
| 2
| 3
|
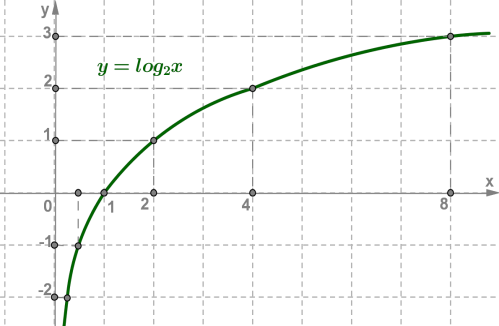
Пример:
2. y=log13x основание 0<13<1
| x
| 9
| 3
| 1
| 13
| 19
|
| y=log13x
| −2
| −1
| 0
| 1
| 2
|

Логарифмическая функция y=logax и показательная функция y=ax, где (a>0,a≠1), взаимно обратны.

Задачи по комбинаторике
Наука, изучающая способы составления и количество множеств и их подмножеств, называется комбинаторикой.
Каждое конкретное подмножество, составленное из элементов данного конечного множества, называется соединениемили выборкой.Если во множестве определено, какой элемент множества за каким следует или какому предшествует, то множество называется упорядоченным. Если в упорядоченном множестве изменить расположение элементов, то мы получим другое, отличное от первого множество.
Выборка — результат отбора, извлечение предпочитаемого из наличного.
Комбинаторная задача состоит в подсчете числа выборок из конечного основного множества элементов M = {a1, а2, а3,..., аn}.Выборки отличаются объемом (т.е. числом элементов, которые надо выбрать), порядком (т.е. упорядоченные или неупорядоченные выборки) и повторениями (есть или нет в выборке повторяющиеся элементы).Мы знаем три основных вида соединений: размещения, перестановки и сочетания.
Размещениями из n элементов по k называются упорядоченные выборки, каждое из которых содержит k элементов из n данного множества. Размещения отличаются друг от друга либо порядком элементов, либо самими элементами.Если некоторые элементы данного множества могут повторяться в размещении, то такие размещения называются кортежами или размещениями с повторениями. Число элементов в размещении называют его длиной.Размещениями с повторениями называют упорядоченную выборку, состоящую из n не обязательно различных элементов. Пусть дано множество M = {a1, а2, а3,..., аn}. Сколько кортежей длины k можно составить из n элементов этого множества? Решение. Первый элемент каждого кортежа мы можем выбрать n способами, записав на первое место любой из n элементов. Второй элемент тоже можно выбрать n способами и т.д. Значит, общее число кортежей из множества n элементов, по k элементов в каждом, будет равно nk. Число кортежей из n по k с учетом их порядка обозначается  , и называют числом размещений с повторениями из n элементов по k:
, и называют числом размещений с повторениями из n элементов по k:  .В примере 1:
.В примере 1:  .
.
Перестановки с повторениями Пример 2. Сколько четырехзначных чисел можно составить из 4 цифр: 1, 2, 3, 4? Решение. Перечислим с помощью схемы все возможные числа: 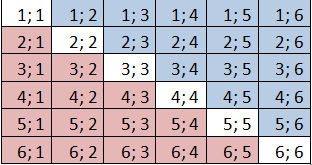 Видим, что всего данных чисел 44 = 256.Данный пример является иллюстрацией к следующему понятию, которое является частным случаем, когда наше основное множество состоит из различных элементов:Размещения с повторениями из n не обязательно различных элементов основного множества по n принято называть перестановками с повторениями. Число перестановок с повторениями обозначают
Видим, что всего данных чисел 44 = 256.Данный пример является иллюстрацией к следующему понятию, которое является частным случаем, когда наше основное множество состоит из различных элементов:Размещения с повторениями из n не обязательно различных элементов основного множества по n принято называть перестановками с повторениями. Число перестановок с повторениями обозначают  .Заметим,
.Заметим, 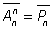 . Общее число перестановок с повторениями из n элементов равно
. Общее число перестановок с повторениями из n элементов равно 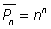 .В примере 2:
.В примере 2: 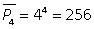 . Пример 3. Сколько семизначных чисел можно составить из 7 цифр: 1; 1; 2; 2; 2; 3; 4? Решение. Заметим, что «1» повторяется 2 раза, «3» — три раза, а «3» и «4» — по одному. На этот случай существует другая формула перестановок с повторениями.В общем случае, когда в нашем основном множестве какие-то элементы могут повторяться используют понятие:
. Пример 3. Сколько семизначных чисел можно составить из 7 цифр: 1; 1; 2; 2; 2; 3; 4? Решение. Заметим, что «1» повторяется 2 раза, «3» — три раза, а «3» и «4» — по одному. На этот случай существует другая формула перестановок с повторениями.В общем случае, когда в нашем основном множестве какие-то элементы могут повторяться используют понятие:
Размещения без повторений (Размещения) Пример 4. Сколько трехзначных чисел, в которых цифры не повторяются, можно составить из 4 цифр: 1, 2, 3, 4? Решение. Перечислим с помощью схемы все возможные числа: 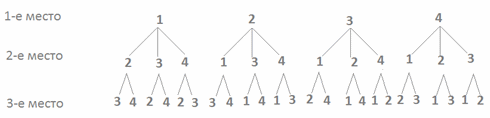 Видим, что всего данных чисел 4·3·2 = 24.Данный пример является иллюстрацией к следующему понятию:
Видим, что всего данных чисел 4·3·2 = 24.Данный пример является иллюстрацией к следующему понятию:
Пусть множество M = {a1, а2, а3,..., аn}. Сколько размещений без повторения элементов, по k элементов в каждом, можно составить из элементов этого множества? Решение. На первое место можно записать любой элемент из М. Значит, имеем n возможностей. На второе место — любой элемент, кроме выбранного на первое место. Итак, при каждом выборе первого элемента для выбора второго имеем n - 1 возможностей, т. е. для выбора двух элементов имеем n(n — 1) возможностей. При каждом выборе первых двух элементов для выбора третьего элемента имеем n — 2 возможностей и т. д. На послед нее k-е место можно записать любой элемент, кроме выбранных k — 1 элементов на предыдущие места, т.е. для его выбора имеем n — (k — 1) = n — k + 1 возможностей. Следовательно, всего размещений из n по k элементов будетAnk = n(n — 1)(n — 2)…(n — k + 1). Полученное выражение состоит из k последовательных натуральных множителей, наибольший из которых равен n. Умножив и разделив полученное выражение на (n — k)! получим: 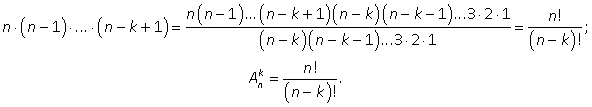
Размещениями называют упорядоченную выборку k элементов, из n различных элементов основного множества.Число всех выборов k элементов из n различных элементов данного множества с учетом их порядка обозначают Аnk и называют числом размещений из n элементов по k.
В примере 4: A43 = 4! / (4-3)! = 4·3·2 = 24.
Перестановки без повторений (Перестановки) Пример 5. Сколько четырехзначных чисел, в которых цифры не повторяются, можно составить из 4 цифр: 1, 2, 3, 4? Решение. Перечислим с помощью схемы все возможные числа: 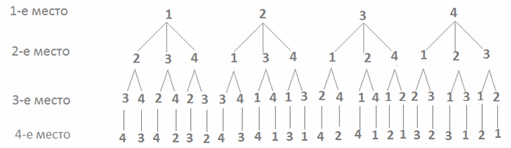 Видим, что всего данных чисел 4 · 3 · 2 · 1 = 24.Данный пример является иллюстрацией к следующему понятию:Размещения из n элементов по n принято называть перестановками. Иначе, перестановки — это упорядоченные множества из n различных элементов основного множества по n. Перестановки отличаются друг от друга только порядком элементов. Число перестановок принято обозначать Рn. Общее число перестановок из n элементов равно Pn = n!.
Видим, что всего данных чисел 4 · 3 · 2 · 1 = 24.Данный пример является иллюстрацией к следующему понятию:Размещения из n элементов по n принято называть перестановками. Иначе, перестановки — это упорядоченные множества из n различных элементов основного множества по n. Перестановки отличаются друг от друга только порядком элементов. Число перестановок принято обозначать Рn. Общее число перестановок из n элементов равно Pn = n!.
В примере 5: P4 = 4! = 4·2·3·1 = 24.
Неупорядоченные выборки.(Одновременный выбор). Сочетания без повторений. (Сочетания) Пример 6. Сколько трехэлементных подмножеств, различающихся хотя бы одним элементом друг от друга и без учета порядка в подмножестве, можно составить из 4 цифр: 1, 2, 3, 4? Решение. Перечислим все полученные подмножества:  (1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4).Видим, что всего получилось 4 подмножества.Данный пример является иллюстрацией к следующему понятию:
(1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4).Видим, что всего получилось 4 подмножества.Данный пример является иллюстрацией к следующему понятию:
Сочетания. Сочетаниями из n элементов по k называются соединения, каждое из которых содержит k элементов из данного множества n элементов и отличается от других хотя бы одним элементом. В сочетаниях нас интересуют только сами элементы множества и не интересует их порядок. Важно, какие конкретно элементы множества входят в каждое соединение.Число сочетаний, т.е. число всех различных подмножеств длины k из данного множества, содержащего n элементов, обозначается Сnk. Легко видеть, что если мы возьмем все сочетания из n по k и в каждом из них упорядочим элементы всеми возможными способами, т.е. из каждого сочетания получим все возможные перестановки, то получим все размещения из n элементов по k. Значит,Ank = Сnk·Pk. Отсюда 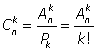 или
или 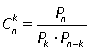 . Иначе
. Иначе 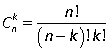 В примере 6:
В примере 6:  .
.
Пример 7. Сколькими способами можно выбрать к предметов из n? Например:
а) одновременно вынимают две карты из колоды: C362 = 36! / (36 - 2)!2! = (36 ∙ 35) / 2 = 630;б) наугад зачеркивают 6 чисел из 49: C496 = 49! / 43! ∙ 6! = 13 980 000;в) случайно отбирают трех человек из 25: C253 = 25! / (22! ∙ 3!) = 2 300.
Сочетания с повторениями Сочетания с повторениями — неупорядоченная выборка, состоящая из n необязательно различных элементов. Обозначается  .
.  ,где n — количество необязательно различных элементов основного множества, k — количество выбираемых. Пример 8. Сколько будет костей в игре домино, если использовать, только четыре цифры 1, 2, 3, 4? Решение. Используем формулу сочетаний с повторениями:
,где n — количество необязательно различных элементов основного множества, k — количество выбираемых. Пример 8. Сколько будет костей в игре домино, если использовать, только четыре цифры 1, 2, 3, 4? Решение. Используем формулу сочетаний с повторениями:  Ответ:
Ответ:
10.Задачи для тренировки
Пример 9. Сколько четырехзначных чисел можно составить из 9 цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9? Решение. Цифры в числах могут повторяться, и число зависит от порядка цифр в его записи. Значит, это размещения с повторениями, т.е. кортежи. Их число  .Ответ:
.Ответ:
6561. Пример 10. В чемпионате участвует 12 команд. Сколькими различными способами могут быть распределены три различные медали? Решение. Это размещения без повторения, т.к. одна команда не может занять два или три места сразу. А123 = 12 · 11 · 10 = 1320.Ответ:
1320. Пример 11. В семье 6 человек. За столом 6 стульев. В семье решили каждый вечер рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений? Решение. Одного человека мы можем посадить только один раз. Значит, имеем перестановки без повторений. Одно размещение от другого может отличаться только порядком размещения людей, т.е. имеем перестановки 6 элементов: P6= 6! = 720.Ответ:
720. Пример 12. Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать капитана команды для математических соревнований и его заместителя? Решение.
1-й способ: на роль капитана может быть выбран любой из 30 учащихся, а его заместитель — любой из 29 оставшихся учеников. Таким образом, получаем 30 · 29 = 870 способов.2-й способ: порядок важен, тогда по формуле числа размещений имеем 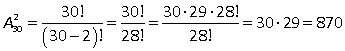 способов.
способов.
Ответ: 870. Пример 13. Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать двоих для участия в математической олимпиаде? Решение.
1-й способ: нам не важно, кто капитан, а кто заместитель, нам нужны всего лишь два участника, поэтому получаем, что у нас каждая пара учащихся в произведении повторяется два раза. Поэтому ответом для второй задачи будет (30 · 29): 2 = 435.
2-й способ: без учета порядка применим формулу числа сочетаний 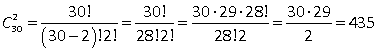 .
.
Ответ:
435. Пример 14. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр? Решение. Так как кнопки нажимаются одновременно, то выбор этих кнопок — сочетание. Отсюда возможно  вариантов.Ответ:
вариантов.Ответ:
120. Пример 15. Три медведя выбегают из дома, догоняя девочку. Сколькими способами они смогут это сделать? Решение. Порядок выбегания из дома задает нумерацию трех медведей числами 1 2 3. Таких нумераций 3! = 6.Ответ:
6. Пример 16. Сколькими способами можно построить пятерых человек в шеренгу? Решение. По формуле числа перестановок имеем Р5 = 5 · 4 · 3 · 2 · 1 = 120.Ответ:
120. Пример 17. Сколькими способами 4 вора могут по одному разбежаться на все 4 стороны? Решение. Стороны фиксированы, например юг, север, запад, восток или для простоты 1, 2, 3, 4. Порядок разбегания по ним задает нумерацию 4-х воров числами 1, 2, 3, 4. Таких нумераций имеется 4! = 24.Ответ:
24. Пример 18. 11 футболистов строятся перед началом матча. 1-м — обязательно капитан, 2-м — обязательно вратарь, а остальные — случайным образом. Сколько существует способов построения? Решение. Капитана и вратаря строить не надо, т.к. их места фиксированы. 9 футболистов (все, кроме капитана и вратаря) надо расставить на 9 мест — с 3-го по 11-е. Всего имеется 9! = 362 880 таких перестановок.Ответ:
362 880. Пример 19. В классе 27 учеников, из которых нужно выбрать троих. Сколькими способами это можно сделать, если:
а) 1-й ученик должен решить задачу, 2-й — сходить за мелом, 3-й — пойти дежурить в столовую;б) им следует спеть хором?
Решение.
а) порядок важен: А273 = 27 · 26 · 25 = 17 550;б) порядок неважен: С273 = (27 · 26 · 25) / (3 · 2) = 2 925.
Ответ: а) 17 550, б) 2 925.
Пример 21. У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими способами бармен может выполнить заказ? Решение. Тут все просто: есть n = 6 сортов, из которых надо выбрать k = 3 сорта. Число сочетаний можно найти по формуле: 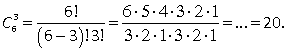 Ответ:
Ответ:
20. Пример 22. В чемпионате по футболу 7 команд. Каждая команда играла с каждой один раз. Сколько всего было игр? Решение. Порядок выбора не имеет значения, т.е. если выбраны две команды, то неважно, какая из них первая, а какая — вторая: 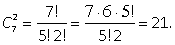 .Ответ:
.Ответ:
21. Пример 23. Сколько всего исходов, если друг за другом из колоды вынимают две карты, не возвращая карту обратно (выбор без возвращения)? Решение.  Ответ:
Ответ:
1260. Пример 24. Сколько существует всего исходов, если из колоды вынимают две карты одновременно? Решение. Порядок не важен, значит: 
Вероятности событий
Все мы довольно часто говорим «это невероятно», «более вероятно, что…», «это маловероятно» и т.д., когда пытаемся спрогнозировать наступление того или иного события. При этом обычно мы опираемся на интуицию, жизненный опыт, здравый смысл. Но часто такие оценки оказываются недостаточными, и бывает важно знать, на сколько или во сколько раз одно случайное событие вероятнее другого. Иными словами нужны точные количественные оценки, нужно уметь численно характеризовать возможность наступления того или иного события. Раздел математики, посвященный исследованию количественных оценок случайных событий, называют теорией вероятностей.
Основные понятия теории вероятностей
Случайное событие (событие) — это некоторое множество (набор) элементарных событий (исходов), которые являются результатом случайного опыта (эксперимента).
Элементарное событие (исход) — это событие, которое нельзя разделить на более простые события.
Пример элементарного события: при одном бросании игральной кости выпало четыре очка.
Пример случайного события: при одном бросании игральной кости выпало четное число очков. Данное событие можно разбить на элементарные события: «выпало два очка», «выпало четыре очка», «выпало шесть очков».
Мы будем рассматривать только случайные опыты (например, бросание игральной кости, раздача игральных карт, розыгрыш лотереи, бросание монеты и т.д.), результатом которых являются элементарные события, шансы которых одинаковы. Такие элементарные события называются равновозможными.
Вероятностью случайного события называют число, выражающее шансы наступления этого события (числовая мера его правдоподобия). Это число равно отношению числа опытов, в которых событие А произошло, к общему числу проведенных равновозможных опытов:  Рассмотрим примеры:Событие G «Лампочка никогда не перегорит» — невозможное событие, его вероятность 0.Событие Q «Летом пойдет снег» — практически невозможное, его вероятность ближе к 0.Событие Z «Завтра я найду на улице миллион рублей» — маловероятное.Событие М «Бутерброд падает всегда маслом вниз» — случайное событие, его вероятность?, как и вероятность выпадения герба при бросании монеты (Событие N).Событие А «Лампочка рано или поздно перегорит» — достоверное событие, с вероятностью 1.Событие В «Зимой бывает снег» — достоверное, его вероятность близка к 1.Посмотрим, как будут данные события располагаться на вероятностной шкале:
Рассмотрим примеры:Событие G «Лампочка никогда не перегорит» — невозможное событие, его вероятность 0.Событие Q «Летом пойдет снег» — практически невозможное, его вероятность ближе к 0.Событие Z «Завтра я найду на улице миллион рублей» — маловероятное.Событие М «Бутерброд падает всегда маслом вниз» — случайное событие, его вероятность?, как и вероятность выпадения герба при бросании монеты (Событие N).Событие А «Лампочка рано или поздно перегорит» — достоверное событие, с вероятностью 1.Событие В «Зимой бывает снег» — достоверное, его вероятность близка к 1.Посмотрим, как будут данные события располагаться на вероятностной шкале: 
Замечание 1. Если число равновозможных событий равно N, то вероятность каждого из них 1/N.
Замечание 2. Если результат случайного эксперимента — три элементарных события a,b,c, а вероятности этих событий Р(a),Р(b),Р(c), то сумма вероятностей всех элементарных события в каждом опыте равна 1, т.е. Р(a) + Р(b) + Р(c) = 1.
Пусть случайное событие А состоит из элементарных событий. Эти элементарные события называют благоприятствующими случайному событию А. Все прочие элементарные события данного опыта, не благоприятствующие событию A, в совокупности представляют новое событие, не благоприятствующее событию А, которое называется событием противоположным событию А (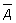 ). События А и
). События А и 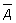 называют взаимно противоположными событиями.
называют взаимно противоположными событиями.
Замечание 3. Взаимно противоположные события одновременно произойти не могут, но какое-либо из них происходит обязательно. Поэтому Р(А) + Р(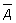 ) = 1. Пример 1.Студент не успел выучить 3 билета из 30. Какова вероятность, что он сдаст экзамен?Решение. По определению вероятности: p = k / n, где k — число благоприятных событий (исходов), n — общее число событий (исходов). k = 30 - 3 = 27, n = 30. Тогда искомая вероятность р = 27 / 30 = 0,9 Второй способ: 3 / 30 = 0,1 — вероятность, что студент не сдаст экзамен, тогда вероятность, что сдаст 1 – 0,1 = 0,9. Ответ:
) = 1. Пример 1.Студент не успел выучить 3 билета из 30. Какова вероятность, что он сдаст экзамен?Решение. По определению вероятности: p = k / n, где k — число благоприятных событий (исходов), n — общее число событий (исходов). k = 30 - 3 = 27, n = 30. Тогда искомая вероятность р = 27 / 30 = 0,9 Второй способ: 3 / 30 = 0,1 — вероятность, что студент не сдаст экзамен, тогда вероятность, что сдаст 1 – 0,1 = 0,9. Ответ:
27 / 30 = 0,9Пример 2.Какова вероятность, стоя с закрытыми глазами перед географической картой мира, выбрать точку на суше, показав на нее указкой, если площадь суши 149,1 млн. км2, а площадь океанов 361,1 млн. км2?Решение. Надо знать какую часть всей площади Земли занимает суша. 149,1 + 361,1 = 510,2 млн. км2. Отношение этих площадей и даст искомую вероятность: 149,1: 510,2 = 0,29. Ответ:
0,29. Геометрическое определение вероятности. Р(А) = S(A) / S(G), где G — произвольная область, А — любая подобласть области G. Пример 3.В квадрат со стороной 4 см «бросают» точку. Какова вероятность, что расстояние от этой точки до ближайшей стороны квадрата будет меньше 1 см?Решение. Закрасим голубым цветом множество точек квадрата, удаленных от ближайшей стороны меньше, чем на 1 см. Площадь закрашенной части квадрата равна 16 см2 - 4 см2 = 12 см2. Отсюда искомая вероятность будет Р = 12 / 16 = 0,75. Ответ:
0,75. Операции с вероятностями
Сложение вероятностей. Событие А  В наступает, если наступают оба события А и В одновременно.Пусть А и В — два события одного случайного опыта. Рассмотрим те элементарные события, которые благоприятствуют событию А, и те элементарные события, которые благоприятствуют событию В. Все вместе эти элементарные события благоприятствуют новому событию, которое называется объединением событий А и В.
В наступает, если наступают оба события А и В одновременно.Пусть А и В — два события одного случайного опыта. Рассмотрим те элементарные события, которые благоприятствуют событию А, и те элементарные события, которые благоприятствуют событию В. Все вместе эти элементарные события благоприятствуют новому событию, которое называется объединением событий А и В.
1. Событие А 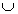 В наступает, если наступает хотя бы одно из событий А или В. Это означает, что наступает либо А, либо В, либо А и В вместе.Пусть А и В — два события одного случайного опыта. Рассмотрим элементарные события, которые благоприятствуют и событию А и событию В. Все вместе эти элементарные события благоприятствуют новому событию, которое называется пересечением событий А и В. Если события А и В не имеют общих благоприятствующих элементарных событий, то они не могут наступить одновременно в ходе одного и того же опыта (еще говорят взаимоисключающие). Такие события называют несовместными, а их пересечение — пустое событие.
В наступает, если наступает хотя бы одно из событий А или В. Это означает, что наступает либо А, либо В, либо А и В вместе.Пусть А и В — два события одного случайного опыта. Рассмотрим элементарные события, которые благоприятствуют и событию А и событию В. Все вместе эти элементарные события благоприятствуют новому событию, которое называется пересечением событий А и В. Если события А и В не имеют общих благоприятствующих элементарных событий, то они не могут наступить одновременно в ходе одного и того же опыта (еще говорят взаимоисключающие). Такие события называют несовместными, а их пересечение — пустое событие.
А) Если события А и В несовместны, то Р(А 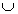 В) = Р(А) + Р (В) Б) Если А и В — любые события, то Р(А
В) = Р(А) + Р (В) Б) Если А и В — любые события, то Р(А 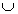 В) = Р(А) + Р (В) - Р(А
В) = Р(А) + Р (В) - Р(А  В)
В)
Пример 4.Мишень представляет три области. Для данного стрелка вероятность попасть в первую область 0,15, во вторую — 0,25, в третью — 0,4.
а) Какова вероятность стрелку попасть с первого выстрела в какую-нибудь из трех областей?б) Какова вероятность промазать с первого выстрела?
Решение.
а) Одновременно попасть в две (три) области при одном выстреле нельзя, т.е. имеем дело с несовместными событиями, поэтому Р = Р1 + Р2 + Р3 = 0,15 + 0, 25 + 0,4 = 0,8. Ответ:
0,8.б) Событие «промазать» противоположно событию «попасть куда-нибудь». Поэтому  = 1 – Р = 1 – 0,8 = 0,2. Ответ: 0,2.
= 1 – Р = 1 – 0,8 = 0,2. Ответ: 0,2.
2. Умножение вероятностей.Случайный выбор — это выбор наудачу одного предмета из группы предметов.Выбор наудачу — это разновидность случайного опыта с равновозможными элементарными событиями. Элементарным событием в таком опыте является извлечение одного предмета из группы. Если в группе N предметов, то каждый из них может быть выбран с вероятностью 1/N. После выбора одного предмета случайный выбор можно продолжить, выбрав второй, третий и т. д. предметы или сразу взять наудачу нужное количество предметов. Собранную таким образом группу называют случайной выборкой. Независимые события — это события, которые не связаны друг с другом, т.е. по наступлению одного из них нельзя судить о вероятности другого. Например, при бросании двух костей результат бросания первой кости не влияет на результат бросания второй.Если события А и В независимы, то Р(А  В) = Р(А) · Р(В).
В) = Р(А) · Р(В).
Пример 7.Какова вероятность, что при бросании двух игральных костей выпадут две шестерки.Решение. Пусть событие А — «на первой кости выпала шестерка», событие В — «на второй кости выпала шестерка», заметим, что Р(А) = Р(В) = 1/6. Общее число элементарных событий 36. Выпадение двух шестерок — новое событие, являющееся пересечением независимых событий А и В. Р(А  В) = 1/36. Получаем, что Р(А
В) = 1/36. Получаем, что Р(А  В) = 1/6 · 1/6 = 1/36 = Р(А) · Р(В). Ответ:
В) = 1/6 · 1/6 = 1/36 = Р(А) · Р(В). Ответ:
3. 1/36.Тригонометрические функции, их свойства и графики.
Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.
Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода 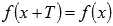 , где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
, где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.
Функция синус y = sin(x).
Изобразим график функции синус, его называют "синусоида".

Свойства функции синус y = sinx.
· Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при  .
.
· Наименьший положительный период функции синуса равен двум пи: 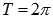 .
.
· Функция обращается в ноль при  , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть 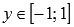 .
.
· Функция синус - нечетная, так как 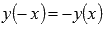 .
.
· Функция убывает при 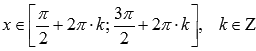 ,
,
возрастает при  .
.
· Функция синус имеет локальные максимумы в точках 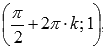 ,
,
локальные минимумы в точках  .
.
· Функция y = sinx вогнутая при  ,
,
выпуклая при  .
.
· Координаты точек перегиба 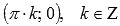 .
.
· Асимптот нет.
Функция косинус y = cos(x).
График функции косинус (его называют "косинусоида") имеет вид:

Свойства функции косинус y = cosx.
· Область определения функции косинус:  .
.
· Наименьший положительный период функции y = cosx равен двум пи: 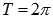 .
.
· Функция обращается в ноль при 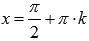 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Область значений функции косинус представляет интервал от минус единицы до единицы включительно: 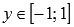 .
.
· Функция косинус - четная, так как  .
.
· Функция убывает при  ,
,
возрастает при  .
.
· Функция y = cosx имеет локальные максимумы в точках 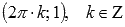 ,
,
локальные минимумы в точках 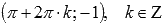 .
.
· Функция вогнутая при 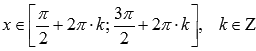 ,
,
выпуклая при  .
.
· Координаты точек перегиба  .
.
· Асимптот нет.
Функция тангенс y = tg(x).
График функции тангенс (его называют "тангенсоида") имеет вид:
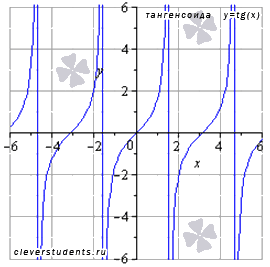
Свойства функции тангенс y = tgx.
· Область определения функции тангенс:  , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
Поведение функции y = tgx на границе области определения 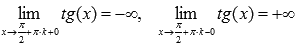
Следовательно, прямые 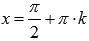 , где
, где  , являются вертикальными асимптотами.
, являются вертикальными асимптотами.
· Наименьший положительный период функции тангенс 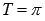 .
.
· Функция обращается в ноль при  , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Область значений функции y = tgx: 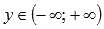 .
.
· Функция тангенс - нечетная, так как 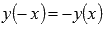 .
.
· Функция возрастает при  .
.
· Функция вогнутая при  ,
,
выпуклая при  .
.
· Координаты точек перегиба 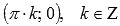 .
.
· Наклонных и горизонтальных асимптот нет.
Функция котангенс y = ctg(x).
Изобразим график функции котангенс (его называют "котангенсоида"):
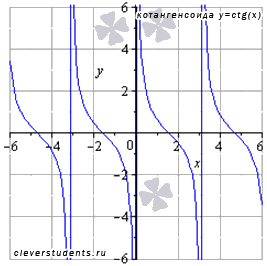
Свойства функции котангенс y = ctgx.
· Область определения функции котангенс: 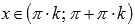 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
Поведение на границе области определения 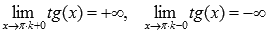
Следовательно, прямые  , где
, где  являются вертикальными асимптотами.
являются вертикальными асимптотами.
· Наименьший положительный период функции y = ctgx равен пи: 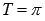 .
.
· Функция обращается в ноль при 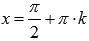 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Область значений функции котангенс: 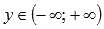 .
.
· Функция нечетная, так как 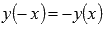 .
.
· Функция y = ctgx убывает при 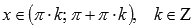 .
.
· Функция котангенс вогнутая при  ,
,
выпуклая при 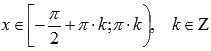 .
.
· Координаты точек перегиба  .
.
· Наклонных и горизонтальных асимптот нет.
ДИФФЕРЕНЦИАЛ
- главная линейная часть приращения функции.
1) Действительная функция y = f{x)действительного переменного наз. дифференцируемой в точке х, если она определена в нек-рой окрестности этой точки и если существует такое число А, что приращение
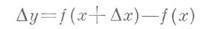
(при условии, что точка х+Ах лежит в упомянутой окрестности) может быть представлено в виде

где  при При
при При  этом А Ах обозначается через dy и наз. дифференциалом функции f(х)в точке х. Д. dy при фиксированном хпропорционален Ах, т. е. является линейной функцией от D х. Дополнительный член a при
этом А Ах обозначается через dy и наз. дифференциалом функции f(х)в точке х. Д. dy при фиксированном хпропорционален Ах, т. е. является линейной функцией от D х. Дополнительный член a при  является, в силу определения, бесконечно малой более высокого порядка по сравнению с D х (и по сравнению с dy, если
является, в силу определения, бесконечно малой более высокого порядка по сравнению с D х (и по сравнению с dy, если 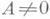 ). Именно в этом смысле Д. и наз. главной частью приращения функции.
). Именно в этом смысле Д. и наз. главной частью приращения функции.
Для функции, дифференцируемой в точке х, 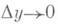 при
при  , т. е. функция, дифференцируемая в некоторой точке, непрерывна в ней. Функция f(x)дифференцируема в точке хв том и только в том случае, если она имеет в этой точке конечную производную
, т. е. функция, дифференцируемая в некоторой точке, непрерывна в ней. Функция f(x)дифференцируема в точке хв том и только в том случае, если она имеет в этой точке конечную производную
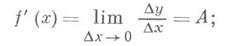
при этом

Существуют непрерывные, но не дифференцируемые функции.
Кроме обозначения dy используется обозначение df (x);тогда предыдущее равенство принимает вид

Приращение аргумента Ах обозначается также через dx и наз. дифференциалом независимого переменного. Поэтому можно писать

Отсюда f(x) =dyldx, т. е. производная равна отношению Д. dy и dx. Если А=0, то  при Dx->0, т. е. Ау и dy при
при Dx->0, т. е. Ау и dy при  являются в случае А неравно 0
являются в случае А неравно 0




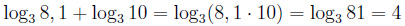
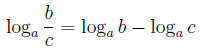
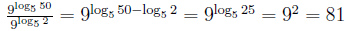
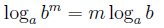

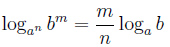 , в частности если m = n, мы получаем формулу:
, в частности если m = n, мы получаем формулу:  , например:
, например: 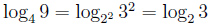
 , частности, если c = b, то
, частности, если c = b, то 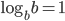 , и тогда:
, и тогда: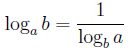
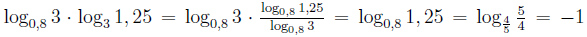







 , и называют числом размещений с повторениями из n элементов по k:
, и называют числом размещений с повторениями из n элементов по k:  .В примере 1:
.В примере 1:  .
. Видим, что всего данных чисел 44 = 256.Данный пример является иллюстрацией к следующему понятию, которое является частным случаем, когда наше основное множество состоит из различных элементов:Размещения с повторениями из n не обязательно различных элементов основного множества по n принято называть перестановками с повторениями. Число перестановок с повторениями обозначают
Видим, что всего данных чисел 44 = 256.Данный пример является иллюстрацией к следующему понятию, которое является частным случаем, когда наше основное множество состоит из различных элементов:Размещения с повторениями из n не обязательно различных элементов основного множества по n принято называть перестановками с повторениями. Число перестановок с повторениями обозначают  .Заметим,
.Заметим, 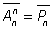 . Общее число перестановок с повторениями из n элементов равно
. Общее число перестановок с повторениями из n элементов равно 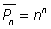 .В примере 2:
.В примере 2: 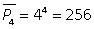 . Пример 3. Сколько семизначных чисел можно составить из 7 цифр: 1; 1; 2; 2; 2; 3; 4? Решение. Заметим, что «1» повторяется 2 раза, «3» — три раза, а «3» и «4» — по одному. На этот случай существует другая формула перестановок с повторениями.В общем случае, когда в нашем основном множестве какие-то элементы могут повторяться используют понятие:
. Пример 3. Сколько семизначных чисел можно составить из 7 цифр: 1; 1; 2; 2; 2; 3; 4? Решение. Заметим, что «1» повторяется 2 раза, «3» — три раза, а «3» и «4» — по одному. На этот случай существует другая формула перестановок с повторениями.В общем случае, когда в нашем основном множестве какие-то элементы могут повторяться используют понятие: Видим, что всего данных чисел 4·3·2 = 24.Данный пример является иллюстрацией к следующему понятию:
Видим, что всего данных чисел 4·3·2 = 24.Данный пример является иллюстрацией к следующему понятию: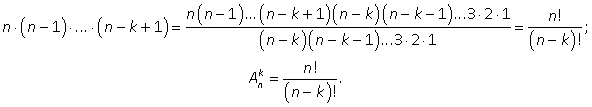
 Видим, что всего данных чисел 4 · 3 · 2 · 1 = 24.Данный пример является иллюстрацией к следующему понятию:Размещения из n элементов по n принято называть перестановками. Иначе, перестановки — это упорядоченные множества из n различных элементов основного множества по n. Перестановки отличаются друг от друга только порядком элементов. Число перестановок принято обозначать Рn. Общее число перестановок из n элементов равно Pn = n!.
Видим, что всего данных чисел 4 · 3 · 2 · 1 = 24.Данный пример является иллюстрацией к следующему понятию:Размещения из n элементов по n принято называть перестановками. Иначе, перестановки — это упорядоченные множества из n различных элементов основного множества по n. Перестановки отличаются друг от друга только порядком элементов. Число перестановок принято обозначать Рn. Общее число перестановок из n элементов равно Pn = n!. (1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4).Видим, что всего получилось 4 подмножества.Данный пример является иллюстрацией к следующему понятию:
(1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4).Видим, что всего получилось 4 подмножества.Данный пример является иллюстрацией к следующему понятию: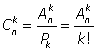 или
или 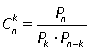 . Иначе
. Иначе 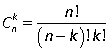 В примере 6:
В примере 6:  .
. .
.  ,где n — количество необязательно различных элементов основного множества, k — количество выбираемых. Пример 8. Сколько будет костей в игре домино, если использовать, только четыре цифры 1, 2, 3, 4? Решение. Используем формулу сочетаний с повторениями:
,где n — количество необязательно различных элементов основного множества, k — количество выбираемых. Пример 8. Сколько будет костей в игре домино, если использовать, только четыре цифры 1, 2, 3, 4? Решение. Используем формулу сочетаний с повторениями:  Ответ:
Ответ: .Ответ:
.Ответ: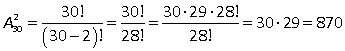 способов.
способов.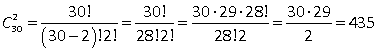 .
. вариантов.Ответ:
вариантов.Ответ: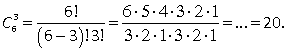 Ответ:
Ответ: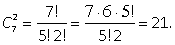 .Ответ:
.Ответ: Ответ:
Ответ:
 Рассмотрим примеры:Событие G «Лампочка никогда не перегорит» — невозможное событие, его вероятность 0.Событие Q «Летом пойдет снег» — практически невозможное, его вероятность ближе к 0.Событие Z «Завтра я найду на улице миллион рублей» — маловероятное.Событие М «Бутерброд падает всегда маслом вниз» — случайное событие, его вероятность?, как и вероятность выпадения герба при бросании монеты (Событие N).Событие А «Лампочка рано или поздно перегорит» — достоверное событие, с вероятностью 1.Событие В «Зимой бывает снег» — достоверное, его вероятность близка к 1.Посмотрим, как будут данные события располагаться на вероятностной шкале:
Рассмотрим примеры:Событие G «Лампочка никогда не перегорит» — невозможное событие, его вероятность 0.Событие Q «Летом пойдет снег» — практически невозможное, его вероятность ближе к 0.Событие Z «Завтра я найду на улице миллион рублей» — маловероятное.Событие М «Бутерброд падает всегда маслом вниз» — случайное событие, его вероятность?, как и вероятность выпадения герба при бросании монеты (Событие N).Событие А «Лампочка рано или поздно перегорит» — достоверное событие, с вероятностью 1.Событие В «Зимой бывает снег» — достоверное, его вероятность близка к 1.Посмотрим, как будут данные события располагаться на вероятностной шкале: 
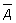 ). События А и
). События А и  В наступает, если наступают оба события А и В одновременно.Пусть А и В — два события одного случайного опыта. Рассмотрим те элементарные события, которые благоприятствуют событию А, и те элементарные события, которые благоприятствуют событию В. Все вместе эти элементарные события благоприятствуют новому событию, которое называется объединением событий А и В.
В наступает, если наступают оба события А и В одновременно.Пусть А и В — два события одного случайного опыта. Рассмотрим те элементарные события, которые благоприятствуют событию А, и те элементарные события, которые благоприятствуют событию В. Все вместе эти элементарные события благоприятствуют новому событию, которое называется объединением событий А и В.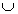 В наступает, если наступает хотя бы одно из событий А или В. Это означает, что наступает либо А, либо В, либо А и В вместе.Пусть А и В — два события одного случайного опыта. Рассмотрим элементарные события, которые благоприятствуют и событию А и событию В. Все вместе эти элементарные события благоприятствуют новому событию, которое называется пересечением событий А и В. Если события А и В не имеют общих благоприятствующих элементарных событий, то они не могут наступить одновременно в ходе одного и того же опыта (еще говорят взаимоисключающие). Такие события называют несовместными, а их пересечение — пустое событие.
В наступает, если наступает хотя бы одно из событий А или В. Это означает, что наступает либо А, либо В, либо А и В вместе.Пусть А и В — два события одного случайного опыта. Рассмотрим элементарные события, которые благоприятствуют и событию А и событию В. Все вместе эти элементарные события благоприятствуют новому событию, которое называется пересечением событий А и В. Если события А и В не имеют общих благоприятствующих элементарных событий, то они не могут наступить одновременно в ходе одного и того же опыта (еще говорят взаимоисключающие). Такие события называют несовместными, а их пересечение — пустое событие. = 1 – Р = 1 – 0,8 = 0,2. Ответ: 0,2.
= 1 – Р = 1 – 0,8 = 0,2. Ответ: 0,2.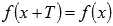 , где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
, где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
 .
.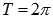 .
. , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.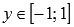 .
.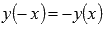 .
.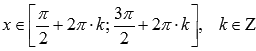 ,
, .
.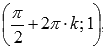 ,
, .
. ,
, .
.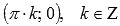 .
.
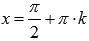 , где
, где  .
.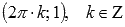 ,
,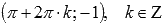 .
. .
.
 , где
, где 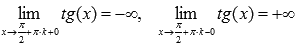
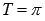 .
.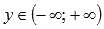 .
. .
. ,
, .
.
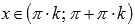 , где
, где 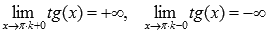
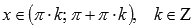 .
. ,
,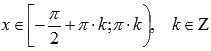 .
.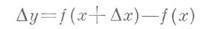

 при При
при При  этом А Ах обозначается через dy и наз. дифференциалом функции f(х)в точке х. Д. dy при фиксированном хпропорционален Ах, т. е. является линейной функцией от D х. Дополнительный член a при
этом А Ах обозначается через dy и наз. дифференциалом функции f(х)в точке х. Д. dy при фиксированном хпропорционален Ах, т. е. является линейной функцией от D х. Дополнительный член a при  является, в силу определения, бесконечно малой более высокого порядка по сравнению с D х (и по сравнению с dy, если
является, в силу определения, бесконечно малой более высокого порядка по сравнению с D х (и по сравнению с dy, если 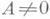 ). Именно в этом смысле Д. и наз. главной частью приращения функции.
). Именно в этом смысле Д. и наз. главной частью приращения функции.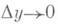 при
при  , т. е. функция, дифференцируемая в некоторой точке, непрерывна в ней. Функция f(x)дифференцируема в точке хв том и только в том случае, если она имеет в этой точке конечную производную
, т. е. функция, дифференцируемая в некоторой точке, непрерывна в ней. Функция f(x)дифференцируема в точке хв том и только в том случае, если она имеет в этой точке конечную производную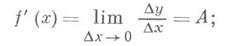



 при Dx->0, т. е. Ау и dy при
при Dx->0, т. е. Ау и dy при  являются в случае А неравно 0
являются в случае А неравно 0


