2.1 Понятие спектральной плотности
Рассмотрим несколько основополагающих определений.
Некий процесс  является стационарным в широком смысле, когда
является стационарным в широком смысле, когда  , равное a, не меняется с течением времени t, а автокорреляционная функция связанного процесса
, равное a, не меняется с течением времени t, а автокорреляционная функция связанного процесса  , определяемого через
, определяемого через  изменяется только при изменении разности моментов времени. В случае, когда n-мерное распределение (при любом конечном n) является независимым от времени в любой его момент, процесс является стационарным в узком смысле [2].
изменяется только при изменении разности моментов времени. В случае, когда n-мерное распределение (при любом конечном n) является независимым от времени в любой его момент, процесс является стационарным в узком смысле [2].
Можно записать ковариационную матрицу конечномерного случайного процесса следующим образом:

| 2.1.1
|
Если процесс стационарен в широком смысле, то для него эта матрица будет зависеть только от следующей разности:
 . .
| 2.1.2
|
Матрицу корреляций можно записать следующим образом:
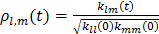 , ,
| 2.1.3
|
кроме того, верно неравенство  .
.
Выражение

| 2.1.4
|
где  – автокорреляционная функция действительного скалярного случайного процесса, называют его спектральным представлением [4]. Данная формула описывает процесс дискретного времени, а для непрерывного используется выражение:
– автокорреляционная функция действительного скалярного случайного процесса, называют его спектральным представлением [4]. Данная формула описывает процесс дискретного времени, а для непрерывного используется выражение:

| 2.1.5
|
В этих формулах  – спектральная функция, а мера, которую она порождает является спектральной мерой.
– спектральная функция, а мера, которую она порождает является спектральной мерой.
Существует теорема, которая гласит:
 – спектральная функция стационарного процесса может быть представлена с помощью разложения Лебега
– спектральная функция стационарного процесса может быть представлена с помощью разложения Лебега  где
где  является абсолютно непрерывной относительно меры Лебега,
является абсолютно непрерывной относительно меры Лебега,  – кусочно-постоянна и обладает счётным количеством разрывов первого рода, а производная
– кусочно-постоянна и обладает счётным количеством разрывов первого рода, а производная  почти в любом месте обращается в ноль, тогда как сама
почти в любом месте обращается в ноль, тогда как сама  непрерывна [6].
непрерывна [6].
Кроме того, стационарный процесс также имеет и спектральную плотность, которая обозначается  . Для этой плотности справедливо выражение:
. Для этой плотности справедливо выражение:

| 2.1.6
|
Выражение

| 2.1.7
|
Является уравнением спектрального коэффициента корреляции на частоте 
2.2 Оценка фрактальной размерности. Показатель Хёрста
Ряды реальных данных, собранных из различных экономических источников, часто представляют собой структуры, лишённые периодичности, где случайность может перемежаться с трендами. Для целесообразности моделирования и прогнозирования подобных временных рядов применяют особые методы, используемые обычно для фрактальной параметризации [11].
Фрактал – это аттрактор развития системы, находящейся в хаосе. В обоих этих объектах реализован принцип самоподобия, то есть даже если размер фрактала будет варьироваться, пропорции будут соблюдены.
Самоподобие можно проиллюстрировать на примере графиков продаж какого-либо товара. Если сравнивать поминутные, почасовые и ежедневные графики, то можно заметить их схожесть и повторяемость форм. Также примером фрактала можно назвать «волны Эллиота», в построении которых затрагивается закон самоподобия [6].
Кроме того, принцип фрактальности подразумевает работу с измерениями отличных от целых, то есть не одно-, дву-, трёхмерными, а такими, которые находятся между ними. Эти нецелочисленные измерения подходят для описания неправильных фигур (фракталов), и носят название фрактальных измерений [9].
Сама по себе фрактальная размерность представляет собой определенное число, которое описывает степень заполнения объектом пространства. Все способы оценки и/или расчета данной величины предполагают вычисление объёма или площади фигуры (фрактала) в пространстве, где она находится.
В настоящее время фрактальная размерность, которую используют в качестве показателя нерегулярности графика фрактала, является одним из важнейших численных индикаторов при исследовании различных сигналов и визуальных данных. Степень неровности контуров того или иного объекта, а также степень нестационарности ряда исследований применяется для нахождения основных характеристик, таких как регулярность/нерегулярность, трендовость, фрактальность, а также для классификации и предсказания будущих значений. Обычно постановка подобных задач в реальности оказывается полезной для медицинских исследований, предсказания индексов в экономике, установление контуров различных объектов и т.п. [14]
Но, несмотря на кажущуюся легкость, оценить фрактальную размерность непросто. Причиной трудности этого процесса является не только хаотичность временных рядов, у которых размерность не является постоянной во времени величиной, но и разница между методами нахождения этой размерности, которые зависят от длины ряда и среди которых не существует универсальных. Отсюда становится понятно, что выявление наиболее точного и максимально простого метода оценки фрактальной размерности – одна из очень важных научных задач.
Для многих реальных рядов отыскать фрактальную размерность аналитическим способом почти невозможно, значит, следует применять численные методы, основанные или непосредственно на самом ряде, или через величины, имеющие прямое и простое отношение к нему [4].
На данный момент существует несколько способов нахождения этой оценки. Считается, что самый простой и обобщённый для различных форм фракталов способ – это клеточное покрытие. К сожалению, его реализация требует значительных временных затрат на вычисление, а также необходимость работы только с длинными временными рядами, где мощность множества точек превышает 100.
Для рядов экономических данных эту оценку фрактальной размерности находят посредством коэффициента Хёрста ( ), который можно показать выражением
), который можно показать выражением  , где
, где  – фрактальная размерность. Сам коэффициент
– фрактальная размерность. Сам коэффициент  находят, используя R/S-анализ. Однако это тоже сопряжено с некоторыми трудностями, потому что подразумевает подсчёт стандартных отклонений на всех отрезках ряда определенной длины [1].
находят, используя R/S-анализ. Однако это тоже сопряжено с некоторыми трудностями, потому что подразумевает подсчёт стандартных отклонений на всех отрезках ряда определенной длины [1].
Показатель Хёрста получил своё название благодаря учёному-гидрологу Герольду Хёрсту.
Существует теорема Бенуа Мандельброта, которая говорит о том, что  – это обратная величина от показателя Хёрста.
– это обратная величина от показателя Хёрста.
Расчётная формула для показателя выглядит следующим образом:

| 2.2.1
|
 - среднеквадратичное отклонение ряда;
- среднеквадратичное отклонение ряда;
 – размах накопленного отклонения;
– размах накопленного отклонения;
 – накопленное отклонение ряда от среднего значения;
– накопленное отклонение ряда от среднего значения;
 – число наблюдений;
– число наблюдений;
 – константа, традиционно принимаемая за 0,5 для не слишком длинных временных рядов.
– константа, традиционно принимаемая за 0,5 для не слишком длинных временных рядов.
Таким образом, в работе [11] была представлена таблица крайних значений показателя, позволяющая определить тип ряда с его помощью.
Очевидно, что на вариации показателя Хёрста оказывают влияние различные факторы, среди которых изменение размаха колебаний  (прямопропорционально), среднеквадратичного отклонения
(прямопропорционально), среднеквадратичного отклонения 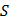 (обратнопропорционально), количества наблюдений (обратнопропорционально).
(обратнопропорционально), количества наблюдений (обратнопропорционально).
Метод оценивания фрактальной размерности с помощью показателя Хёрста имеет и свои недостатки. Одним из них является необходимость в знании значений ряда за продолжительный промежуток времени, то есть, мощность множества данных должна насчитывать сотни величин, характеризующих исследуемый признак. Ещё одним из этих недостатков можно назвать требование, что значения исходного ряда должны иметь нормальное распределение, что в реальных условиях – достаточно редкое явление. В случае несоблюдения этих условий оценки, полученные вышеприведенной формулой, могут оказаться неверными.
Кроме того, хоть значение фрактальной размерности  и характеризует весь ряд в целом, оно не означает, что на протяжении ряда его поведение не меняется, ведь тренды могут быть разнонаправленными, а на отдельных участках ряда вообще может наблюдаться случайность (или, если она была выявлена прежде, случайные колебания могут переходить в трендовые) [11].
и характеризует весь ряд в целом, оно не означает, что на протяжении ряда его поведение не меняется, ведь тренды могут быть разнонаправленными, а на отдельных участках ряда вообще может наблюдаться случайность (или, если она была выявлена прежде, случайные колебания могут переходить в трендовые) [11].
Порой в работе с реальными данными показатель Хёрста может принимать аномальные значения. Ввиду приведённых выше причин, полученное значение может оказаться ошибочным и необоснованным. Чтобы убедиться, что оценка получена верно, можно вспомнить, что Шейнкман и Ле Барон разработали тест для корреляционной размерности, который лёг в основу теста для проверки показателя Хёрста [8].
Начнём с того, что в случае, если  значительно превосходит или превышает 0,5, то на это может быть только две причины:
значительно превосходит или превышает 0,5, то на это может быть только две причины:
a) Ряд имеет долговременную память, то есть между наблюдениями существует корреляция;
b) Анализ фрактальности с помощью формулы Хёрста несостоятелен в изучаемом случае, а значит долговременной памяти может не быть.
Последний пункт может быть вызван нехваткой реальных данных, взятых для изучения, особенно учитывая отсутствие чётких указаний на их минимальное количество. Однако рассматриваемый ряд всё равно
a) Содержит в себе показатель Хёрста, не равный 0,5;
b) Является независимым процессом с толстыми хвостами.
Чтобы проверить состоятельность применения формулы, можно использовать случайное перемешивание данных. Тогда частотное распределение останется прежним, и, при независимости наблюдений, показатель Хёрста тоже не изменится. Однако при наличии долговременной памяти (корреляции соседних наблюдений) порядок данных играет огромную роль. Поэтому вычисленный по новому ряду показатель Хёрста будет не только значительно отличаться от исходного в меньшую сторону, но и стремиться к 0,5 [8].
Помимо неэффективного в некоторых случаях показателя Хёрста, иногда используются и другие способы оценивания фрактальной размерности.
Один из них основан на вычислении клеточной размерности. Это осуществляется путём определения углового коэффициента графика  , где
, где

| 2.2.2
|
Искомая размерность D будет носить название клеточной размерности, если она вычисляется через количество клеток (ячеек), требуемых для покрытия множества, с учётом величины ячейки.
Второй способ базируется на вычислении стандартного отклонения с учётом различных степеней приведения к среднему [5].
Если имеется временной ряд  , то для него могут быть найдены обобщённые временные ряды m. Для этого используется формула
, то для него могут быть найдены обобщённые временные ряды m. Для этого используется формула
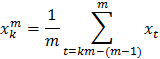
| 2.2.3
|
В результате имеется новый ряд 
Если известно, что ряд самоподобный, то для него стандартное отклонение полученного ряда вычисляется по формуле

| 2.2.4
|
где  вычисляется по формуле
вычисляется по формуле  . Здесь
. Здесь  , как и выше, - показатель Хёрста. Он может быть вычислен через определение
, как и выше, - показатель Хёрста. Он может быть вычислен через определение  как углового коэффициента в графике функции
как углового коэффициента в графике функции  в качестве функции от
в качестве функции от  То есть данный способ основывается на подсчёте стандартного отклонения для разных степеней приведения к среднему для агрегированных рядов.
То есть данный способ основывается на подсчёте стандартного отклонения для разных степеней приведения к среднему для агрегированных рядов.



 является стационарным в широком смысле, когда
является стационарным в широком смысле, когда  , равное a, не меняется с течением времени t, а автокорреляционная функция связанного процесса
, равное a, не меняется с течением времени t, а автокорреляционная функция связанного процесса  , определяемого через
, определяемого через  изменяется только при изменении разности моментов времени. В случае, когда n-мерное распределение (при любом конечном n) является независимым от времени в любой его момент, процесс является стационарным в узком смысле [2].
изменяется только при изменении разности моментов времени. В случае, когда n-мерное распределение (при любом конечном n) является независимым от времени в любой его момент, процесс является стационарным в узком смысле [2].
 .
.
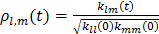 ,
,
 .
.
 – автокорреляционная функция действительного скалярного случайного процесса, называют его спектральным представлением [4]. Данная формула описывает процесс дискретного времени, а для непрерывного используется выражение:
– автокорреляционная функция действительного скалярного случайного процесса, называют его спектральным представлением [4]. Данная формула описывает процесс дискретного времени, а для непрерывного используется выражение:
 – спектральная функция, а мера, которую она порождает является спектральной мерой.
– спектральная функция, а мера, которую она порождает является спектральной мерой. где
где  является абсолютно непрерывной относительно меры Лебега,
является абсолютно непрерывной относительно меры Лебега,  – кусочно-постоянна и обладает счётным количеством разрывов первого рода, а производная
– кусочно-постоянна и обладает счётным количеством разрывов первого рода, а производная  почти в любом месте обращается в ноль, тогда как сама
почти в любом месте обращается в ноль, тогда как сама  . Для этой плотности справедливо выражение:
. Для этой плотности справедливо выражение:


 ), который можно показать выражением
), который можно показать выражением  , где
, где  – фрактальная размерность. Сам коэффициент
– фрактальная размерность. Сам коэффициент 
 - среднеквадратичное отклонение ряда;
- среднеквадратичное отклонение ряда; – размах накопленного отклонения;
– размах накопленного отклонения; – накопленное отклонение ряда от среднего значения;
– накопленное отклонение ряда от среднего значения; – число наблюдений;
– число наблюдений; – константа, традиционно принимаемая за 0,5 для не слишком длинных временных рядов.
– константа, традиционно принимаемая за 0,5 для не слишком длинных временных рядов. (прямопропорционально), среднеквадратичного отклонения
(прямопропорционально), среднеквадратичного отклонения 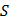 (обратнопропорционально), количества наблюдений (обратнопропорционально).
(обратнопропорционально), количества наблюдений (обратнопропорционально).



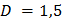



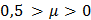
 , где
, где
 , то для него могут быть найдены обобщённые временные ряды m. Для этого используется формула
, то для него могут быть найдены обобщённые временные ряды m. Для этого используется формула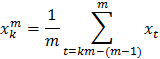


 вычисляется по формуле
вычисляется по формуле  . Здесь
. Здесь  в качестве функции от
в качестве функции от  То есть данный способ основывается на подсчёте стандартного отклонения для разных степеней приведения к среднему для агрегированных рядов.
То есть данный способ основывается на подсчёте стандартного отклонения для разных степеней приведения к среднему для агрегированных рядов.


