

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
В системах с дискретным временем, которые традиционно называются каскадами, поведение системы (или, что-то же самое, траектория системы в фазовом пространстве) описывается последовательностью состояний. В системах с непрерывным временем, которые традиционно называются потоками, состояние системы определено для каждого момента времени на вещественной или комплексной оси. Каскады и потоки являются основным предметом рассмотрения в символической и топологической динамике.
Динамическая система (как с дискретным, так и с непрерывным временем) часто описывается автономной системой дифференциальных уравнений, заданной в некоторой области и удовлетворяющей там условиям теоремы существования и единственности решения дифференциального уравнения. Положениям равновесия динамической системы соответствуют особые точки дифференциального уравнения, а замкнутые фазовые кривые — его периодическим решениям.
Основное содержание теории динамических систем — это исследование кривых, определяемых дифференциальными уравнениями. Сюда входит разбиение фазового пространства на траектории и исследование предельного поведения этих траекторий: поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств (многообразий). Важнейшие понятия теории динамических систем — устойчивость (способность системы сколь угодно долго оставаться около положения равновесия или на заданном многообразии) и грубость (сохранение свойств при малых изменениях структуры динамической системы; “грубая система — это такая, качественный характер движений которой не меняется при достаточно малом изменении параметров”).
|
|
Привлечение вероятностно-статистических представлений в эргодической теории динамических систем приводит к понятию динамической системы с инвариантной мерой.
Современная теория динамических систем является собирательным названием для исследований, где широко используются и эффективным образом сочетаются методы из различных разделов математики: топологии и алгебры, алгебраической геометрии и теории меры, теории дифференциальных форм, теории особенностей и катастроф.
Для задания динамической системы необходимо описать её фазовое пространство X, множество моментов времени T и некоторое правило, описывающее движение точек фазового пространства со временем. Множество моментов времени T может быть, как интервалом вещественной прямой (тогда говорят, что время непрерывно), так и множеством целых или натуральных чисел (дискретное время). Во втором случае «движение» точки фазового пространства больше напоминает мгновенные «скачки» из одной точки в другую: траектория такой системы является не гладкой кривой, а просто множеством точек, и называется обычно орбитой. Тем не менее, несмотря на внешнее различие, между системами с непрерывным и дискретным временем имеется тесная связь: многие свойства являются общими для этих классов систем или легко переносятся с одного на другой.
Расчетная часть.
3.2.1 Постановка задачи моделирование системы. Целью разработки данного раздела является ознакомление с методикой моделированием анализа и синтеза динамической системы заданной структуры и её параметризация.
Задачи моделирование системы:
1) Разработка математической модели каждого элемента.
2) Исследование свойств и характеристик по разработанной математической модели.
3) Структурный анализ системы и разработка её математической модели.
4) Освоение методики моделирования устойчивости системы и анализ устойчивости исходной системы.
5) Освоение методики синтеза системы обеспечивающий её устойчивость.
|
|
3.2.2 Исходная система представляет собой последовательное соединение элементов, и она относится к классу систем с последовательным соединением.
Другие группы таких систем являются системы с параллельным соединением элементов и системой обратной связи.
Системы с последовательным соединением элементов - такие системы в которых выходная величина предыдущего элемента является входной величиной последующего.
Математическая модель системы с последовательным соединением выражается как произведение математической модели каждого элемента.
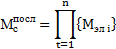
Математическая модель системы является исходной информацией для анализа её поведения в частности устойчивости системы.
Несмотря на многообразие физических моделей системы их поведение в форме математического выражения можно классифицировать в конечные группы.
3.2.3 В теории моделирования в частности динамических систем разработаны различные подходы анализа свойств и их мат. модели.
Одним из распространенных и наглядных подходов исследования свойств элементов является частотный метод.
Xвх Эл-т Хвых
Хвх Хвых
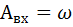
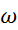
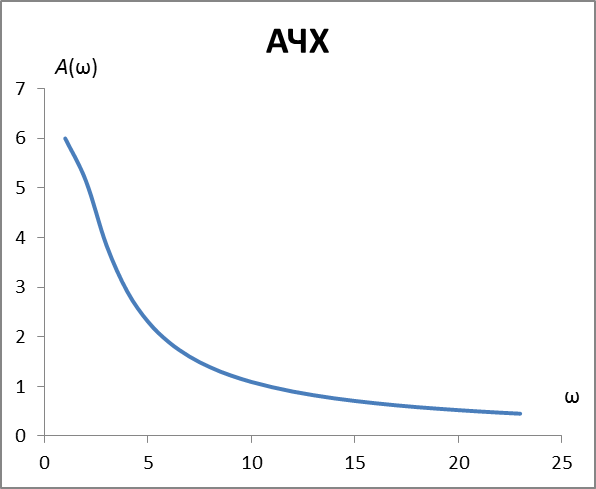
АЧХ
АФХ
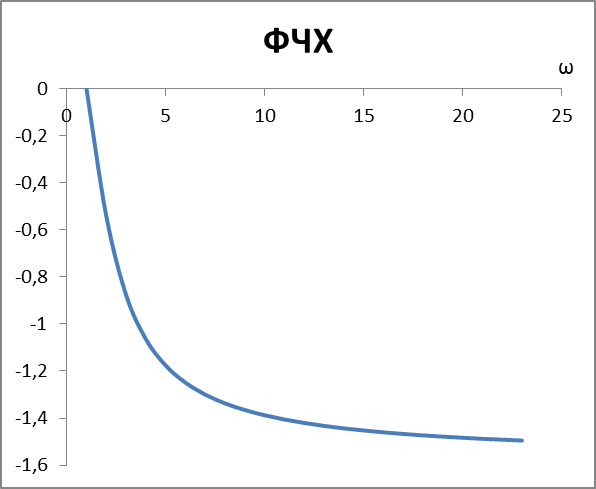
ФЧХ
Рис. 3.2. Частотный метод.
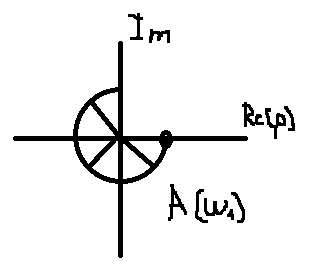
Рис. 3.3. Частотный метод.
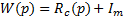 (p)
(p)
АФХ =>
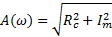
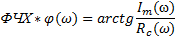
В результате данного исследования устанавливаются следующие характеристики:
АЧХ - амплитудно-частотная характеристика
ФЗХ - фазо-частотная характеристика
АФХ - амплитудно-фазовая характеристика
Для получения этих характеристик дифференциальное уравнение элементов необходимо преобразовать в его передаточную функцию. Она будет являться математической моделью, но другой формы.
Раскроем суть этого преобразования. Пусть задана математическая модель в виде обобщенного дифференциального уравнения.
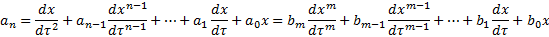
Левая часть этого уравнения показывает изменения выходной величины во времени.
Правая часть уравнения показывает характер изменения входного воздействия.
Частотный подход к исследованию свойств системы предполагает переход от данного вида уравнения к передаточной функции. Первым этапом перехода является преобразования дифференциального уравнения в уравнение операторной формы. Для этого используется преобразование Лапласа, интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
|
|
Чтобы осуществить этот переход необходимо оригинал преобразовать в изображение.
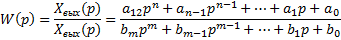
Идентификация элементов.
Вариант 3:
| K 1 | K 2 | T 2 | T 3 | K 4 | K 5 |
| 1 | 3 | 4 | 8 | 5 | 2 |
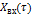
|
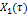
|
| Элемент №1 |
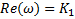
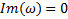
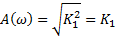
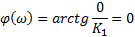
|
|
| АФХ | |
| АЧХ | ФЧХ | Im | Re |
| 1 | 0 | 0 | 8 |

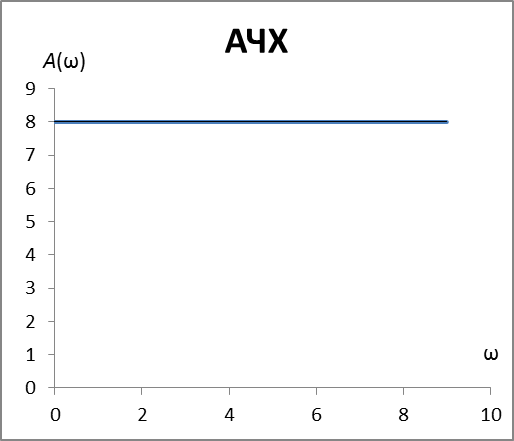
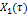
|
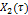
|
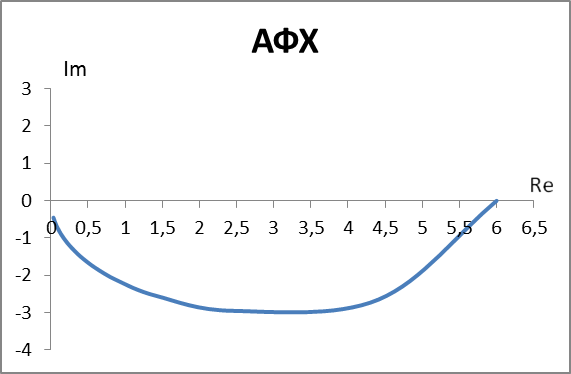
| Элемент №2 |
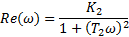
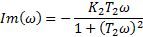
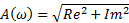
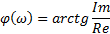
| АФХ | ||||
| АЧХ | ФЧХ | Im | Re | ω |
| 6 | 0 | 0 | 6 | 0 |
| 5,14 | -0,54 | -2,65 | 4,41 | 0,1 |
| 3,84 | -0,88 | -2,95 | 2,46 | 0,2 |
| 2,91 | -1,06 | -2,55 | 1,42 | 0,3 |
| 2,31 | -1,18 | -2,13 | 0,89 | 0,4 |
| 1,90 | -1,25 | -1,80 | 0,60 | 0,5 |
| 1,61 | -1,30 | -1,55 | 0,43 | 0,6 |
| 1,39 | -1,34 | -1,35 | 0,32 | 0,7 |
| 1,22 | -1,37 | -1,20 | 0,25 | 0,8 |
| 1,09 | -1,39 | -1,07 | 0,20 | 0,9 |
| 0,99 | -1,41 | -0,97 | 0,16 | 1 |
| 0,90 | -1,42 | -0,89 | 0,13 | 1,1 |
| 0,83 | -1,43 | -0,82 | 0,11 | 1,2 |
| 0,76 | -1,44 | -0,76 | 0,10 | 1,3 |
| 0,71 | -1,45 | -0,70 | 0,08 | 1,4 |
| 0,66 | -1,46 | -0,66 | 0,07 | 1,5 |
| 0,62 | -1,47 | -0,62 | 0,06 | 1,6 |
| 0,59 | -1,47 | -0,58 | 0,06 | 1,7 |
| 0,55 | -1,48 | -0,55 | 0,05 | 1,8 |
| 0,52 | -1,48 | -0,52 | 0,05 | 1,9 |
| 0,50 | -1,49 | -0,50 | 0,04 | 2 |
| 0,47 | -1,49 | -0,47 | 0,04 | 2,1 |
| 0,45 | -1,50 | -0,45 | 0,03 | 2,2 |
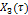
|
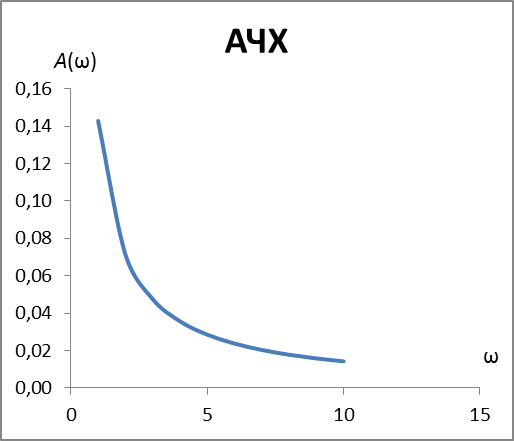
| Элемент №3 |
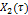
|
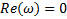
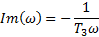
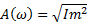
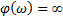
| АФХ | ||||
| АЧХ | ФЧХ | Im | Re | ω |
| 0,14 | 0 | -0,14 | 0 | 1 |
| 0,07 | 0 | -0,07 | 0 | 2 |
| 0,05 | 0 | -0,05 | 0 | 3 |
| 0,04 | 0 | -0,04 | 0 | 4 |
| 0,03 | 0 | -0,03 | 0 | 5 |
| 0,02 | 0 | -0,02 | 0 | 6 |
| 0,02 | 0 | -0,02 | 0 | 7 |
| 0,02 | 0 | -0,02 | 0 | 8 |
| 0,02 | 0 | -0,02 | 0 | 9 |
| 0,01 | 0 | -0,01 | 0 | 10 |


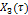
|
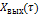
|
| Элемент №4 |
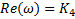
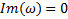
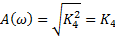
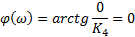
|
|
| АФХ | |
| АЧХ | ФЧХ | Im | Re |
| 2 | 0 | 0 | 2 |
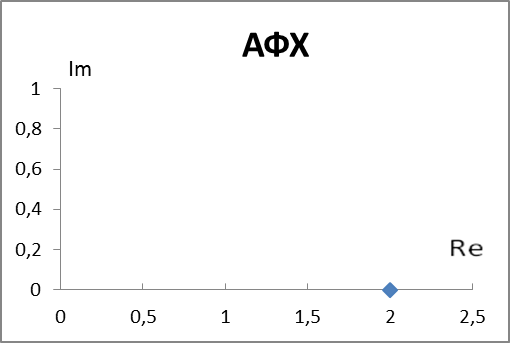
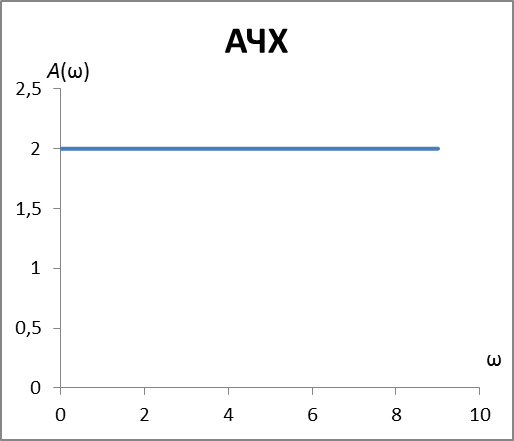

3.2.4 Структурное моделирование систем.
Для исследования системы (структура которой известна) необходимо получить её математическую модель. Эта модель определяется в свою очередь, моделями каждого элемента и схемой соединения этих элементов в системе. Несмотря на многообразие возможных схем соединения элементов в системе в теории систем их классифицируют на 3 группы:
|
|
1) Система с последовательным соединением элементов. Схема такого соединения задана в настоящей работе.
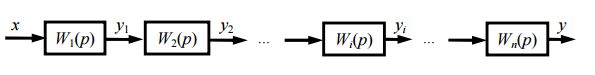
Рис.3.4. Структурная схема последовательного соединения звеньев.
2) Параллельно соединение элементов системы
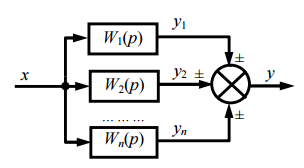
Рис.3.5. Структурная схема параллельного соединения звеньев.
3) Встречно-параллельное соединение.
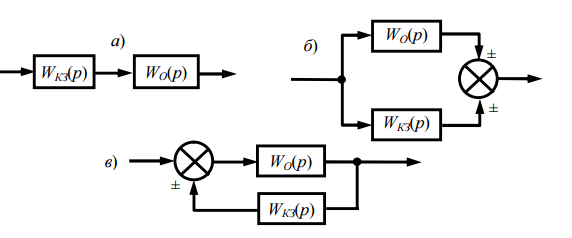
Рис.3.6. Структурные схемы типов коррекции: а- последовательная; б- параллельная; в-с помощью дополнительных обратных связей.
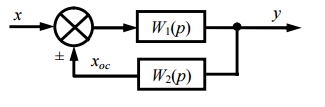
Рис.3.7. Структурная схема звена охваченного обратной связью.
Реальные системы могут содержать все виды соединений. Тогда они называются - схема с комбинированным соединением элементов.
Целью структурного моделирования является получение математической модели всех систем.
В теории систем такие модели определяются моделями каждого элемента.
Iгр
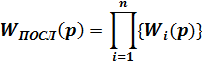
IIгр
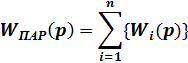
IIIгр
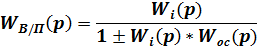
|
|
|

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!