Теоретические основы модального управления

 

Поведение в системе автоматического управления определяется корнями характеристического уравнения, которым, в свою очередь, соответствуют составляющие свободного движения системы, называемые «модами». Модальное управление – это такое управление, когда достигается требуемый характер переходных процессов за счет обеспечения необходимого расположения корней характеристического полинома на комплексной плоскости. При этом задача сводится к определению коэффициентов соответствующих обратных связей по состоянию объекта, а не путем применения корректирующих звеньев в прямой цепи САУ.

Это управление применяется тогда, когда все составляющие вектора состояния объекта управления доступны непосредственному измерению (полная управляемость). Для линейных динамических систем корни замкнутой системы можно смещать в любые желаемые положения при законе управления в виде линейной функции переменных состояния. Эта же задача может быть решена и при использовании в законе управления лишь части переменных состояния (неполная управляемость), если для управления использовать не один, а несколько входов объекта, когда используется подача внешних воздействий в нескольких различных точках.

Следует заметить, что термин “объект управления” следует воспринимать в более широком смысле, чем это принято в классической теории автоматического управления. Сюда следует относить исполнительные и рабочие органы, предшествующие им усилители и преобразователи, принимая их выходные сигналы в качестве составляющих выходного вектора объекта.

Расчет и конструирование модальных регуляторов проводится в следующей последовательности. Пусть полностью управляемый и наблюдаемый объект описывается следующими уравнениями в векторно-матричной форме:

 

                                           (1.1)

где X – n-мерный вектор переменных состояния объекта (n – порядок объекта); Y и U – векторы выходной переменной и управления; A, B и C – матрицы соответственно коэффициентов характеристического уравнения, управления и наблюдения.

Сформируем обратную связь следующим образом:

     U=K(G – LX),                                               (1.2)

где G – вектор задающих сигналов; K – матрица коэффициентов усиления промежуточного регулятора (усилителя); L – матрица коэффициентов обратных связей.

Тогда обобщая уравнения замкнутой системы (1.1) и (1.2) получаем

                                       (1.3)

или в виде

                                                      (1.4)

где F=A – BKL.

Характеристическое уравнение полученной замкнутой системы определяется следующим образом:

       D(p)=det ,                                                    (1.5)

где I – единичная матрица размерности

Поскольку собственные числа матрицы однозначно определяют коэффициенты характеристического полинома, задача может быть сформулирована следующим образом: для управляемой системы (1.1) с характеристическим полиномом  найти вектор L коэффициентов обратных связей и предварительный коэффициент усиления K, чтобы замкнутая система (1.4) имела желаемую стандартную форму характеристического полинома (1.5) с заданными коэффициентами l _i.

Процедура расчета коэффициентов l ₁,..., l _n проводится в следующей последовательности:

· выбираем желаемое распределение корней характеристического уравнения, то есть выбираем желаемую стандартную форму характеристического полинома замкнутой системы. С целью сокращения объема вычислений для случаев объектов высокого порядка целесообразно применить описание объекта в канонической управляемой форме Фробениуса;

· находим характеристический полином с помощью формулы (1.5);

· коэффициенты этого полинома будут зависеть от неизвестных пока параметров l _i и коэффициента усиления промежуточного усилителя K;

· приравнивая коэффициенты при одинаковых степенях p полиномов, полученных на первом и втором шагах, получаем систему уравнений для определения неизвестных параметров l _i. Решив ее при известных остальных параметрах системы (матрицы А,B,С), находим искомые параметры модального регулятора (элементы матрицы L). При этом К промежуточного усилителя находится из условия получения требуемых переменных состояния в установившемся режиме, т.е. .

Наиболее распространенными из стандартных форм характеристического полинома являются: фильтр Чебышева, распределение Бесселя, распределение Баттерворта, биномиальное распределение, когда при порядке системы n берется характеристический полином в следующем виде:

              D(p)=(p+w)ⁿ = 0,                                              (1.6)

где w – среднегеометрический корень.

Распределение характеризуется наличием n кратных действительных и отрицательных корней, количественно равных среднегеометрическому корню. Характеристические уравнения для этого распределения имеют вид, представленный в таблице1.1.

Таблица 1.1

Порядок системы	Время регулирования, tp	Характеристическое уравнение
1	3/ω	D(p) = p + ω
2	4,5/ω	D(p) = p2 + 2ω p + ω2
3	6/ω	D(p) = p3 + 3ω p2 + 3ω2 p + ω3
4	7,6/ω	D(p) = p4 + 4ω p3 + 6ω2 p2 + 4ω3 p + ω4

 

Значения коэффициентов характеристического уравнения D(p) в зависимости от порядка системы в распределении Баттерворта сведены в таблицу 1.2.

Таблица 1.2

Порядок системы	Перерег.  %	Время рег. tp	Характеристическое  уравнение
1	0	3/w	D(p)=p+w
2	4,3	3/w	D(p)=p2+1.4wp+w2
3	8	6/w	D(p)=p3+2wp2+2w2p+w3
4	11	6,8/w	D(p)=p4+2.6wp3+3.4w2p2+2.6w3p+w4

 

При этом во всех случаях значение w выбирают исходя из требуемого быстродействия и перерегулирования системы с учетом ограничений на управление и переменные состояния.

 

Пример расчета модального регулятора

Рассмотрим задачу синтеза обратной связи для системы управления электроприводом перемещения. Пусть упрощенная линейная модель разомкнутой системы управления описывается дифференциальным уравнением вида

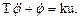
где: Т – постоянная времени привода, учитывающая его инерционность; к – общий статический коэффициент передачи канала управления; j и w – соответственно угол поворота и угловая скорость электродвигателя; u - управляющий сигнал (напряжение управляемого источника питания).

           Переходя к изображениям по Лапласу, получим

 

 

где к₁×к₂ = к. Представим объект управления структурной схемой в виде последовательного соединения апериодического и интегрирующего звеньев рис.1.1.

 

 

Рис.1.1

 

Уравнения объекта в скалярной форме будут иметь вид

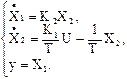
Здесь 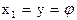  - переменная состояния, пропорциональная углу поворота электропривода;  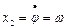 - переменная состояния, пропорциональная угловой скорости электропривода.

Уравнение объекта в векторно-матричной форме согласно (1.1)

Отсюда находим

 

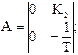
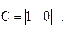
Корни характеристического уравнения разомкнутой системы  следовательно, объект управления является нейтральным. Для обеспечения заданного перемещения введем линейные обратные связи по углу и угловой скорости 

 

u (t) = – l ₁ x ₁(t) – l ₂ x ₂(t) + k ₀ g (t),

 

где g – задаваемое значение перемещения.

Тогда замкнутая система с модальным управлением будет иметь вид, показанный на рис.1.2.

 

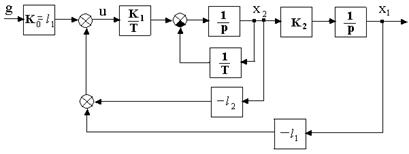
Рис.1.2

 

Она описывается дифференциальными уравнениями в скалярной форме

 

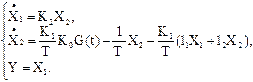                                  (1.7)

Коэффициент усиления предварительного усилителя К₀ найдем из условия обеспечения установившегося перемещения (заданного), т.е. y=x₁=g. При этом

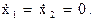
Тогда из уравнения (1.7) получим К₀ = l_1.

                   Характеристическое уравнение замкнутой САУ с неизвестными параметрами l_i модального регулятора найдем из уравнения (1.7)

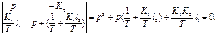       (1.8)

 

           Если для САУ второго порядка принять коэффициенты желаемого характеристического уравнения (1.7) в соответствии с распределением Баттерворта, т. е.

 

D(p) = p² +1,4 w p + w² = 0 и t_p =3/w,              (1.9)

 

то предварительно задавшись требуемым временем переходного процесса t_p, приравнивая коэффициенты при одинаковых степенях оператора р в уравнениях (1.8) и (1.9), получим следующие коэффициенты обратных связей (модального регулятора):

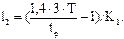                     (1.10)

 

Если для САУ второго порядка принять коэффициенты желаемого характеристического уравнения (1.7) в соответствии с биномиальным распределением, т. е.

 

D(p) = p² +2 w p + w² = 0 и t_p @ 3/w,              (1.11)

 

то предварительно задавшись требуемым временем переходного процесса t_p, приравнивая коэффициенты при одинаковых степенях оператора р в уравнениях (1.8) и (1.11), получим следующие коэффициенты обратных связей (модального регулятора):

 

                   (1.12)

 

           Для приведенной САУ модального управления примем следующие значения параметров: T=0,2 c.; k₁=10; k₂=0,1; t_p=0,3 c. Тогда коэффициенты обратных связей модального регулятора, рассчитанные по формулам (1.10) и (1.12), будут иметь значения:

- для биномиального распределения - l₁= 20; l₂= 0,3;

- для распределения Баттерворта - l₁= 20; l₂= 0,18.

 

 

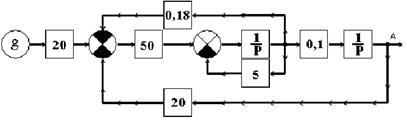
Рис.1.3

На рис.1.3 приведена схема модели системы управления с модальным регулятором, настроенным на распределение Баттерворта.

           На рис. 1.4 приведены результаты моделирования САУ с модальным управлением в среде пакета прикладных программ SyAn. На графиках приведены переходные процессы при g(t) = 1 для биномиального распределения (рис.1.4,а) и для распределения Баттерворта (рис.1.4,б).

 

 

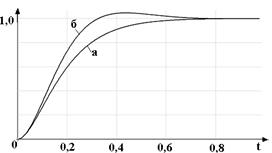
Рис.1.4

 

При использовании распределения Баттерворта время переходного процесса меньше, чем при использовании биномиальной настройки, но в тоже время появляется перерегулирование. При использовании биномиальной стандартной настройки и стандартного распределения Баттерворта ошибка системы регулирования с нейтральным объектом стремится к нулю. В обоих случаях быстродействие выше, чем при классических оптимальных настройках регуляторов (модульной и симметричной).