Эта глава относится к теории катастроф и их роли в экономической динамике. Теория катастроф была очень популярной в 70-х годах ХХ века и была признана многообещающей методикой моделирования разрывных скачков в переменных состояния динамических систем. В приложениях этой теории изучались такие интересные эмпирические вопросы, как внезапное проявление агрессивности у различных биологических разновидностей, крах фондового рынка, опрокидывание судов, и т.д. Все эти примеры описывают явления, которые характеризуются резким, разрывным изменением переменных.
После первоначального проявления интереса к исследованиям, было показано, что теория катастроф не достаточно хорошо подходит для исследований как аналитический инструмент, и что она в лучшем случае способна играть роль эвристического инструмента при подготовке теории. Хотя некоторые экономические примеры применения теории катастроф существуют, не совсем ясно, будут ли дальнейшие исследования в области экономической динамики плодотворно влиять на развитие этой теории. И, тем не менее, некоторое введение в теорию катастроф не помешает, поскольку существует некоторая путаница в определении качественных различий между хаосом и катастрофами.
Хотя название «теория катастроф» предполагает исследование событий, сравнимых со стихийными бедствиями, эта теория имеет дело с менее эффектным поведением. Теория катастроф представляет собой попытку систематизировать явление бифуркаций в некоторых семействах структурно стабильных функций. Выбор термина «теория катастроф» станет очевидным, когда будет показано, что в определенной точке переменные состояния «перескакивают» к новым равновесным значениям в неожиданной (катастрофической) манере.
Основные понятия
Предметом изучения теории катастроф является классификация внезапных скачков или «катастроф» в поведении динамических систем. Рассмотрим семейство одномерных функций, параметризированных  -размерным вектором
-размерным вектором 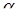 :
:
 . (12.1)
. (12.1)
Пусть  будет аналитической функцией, которую можно записать в виде многочлена:
будет аналитической функцией, которую можно записать в виде многочлена:
 , (12.2)
, (12.2)
с некоторыми  возможно равными нулю.
возможно равными нулю.
Для заданного  график многочлена имеет различную форму, если некоторые параметры исчезают. К примеру рассмотрим случай, когда
график многочлена имеет различную форму, если некоторые параметры исчезают. К примеру рассмотрим случай, когда  с
с  ,
, 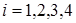 . График
. График 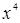 достаточно сильно отличается от графика
достаточно сильно отличается от графика  . В зависимости от количества исчезающих параметров i, могут возникнуть один или несколько экстремумов функции.
. В зависимости от количества исчезающих параметров i, могут возникнуть один или несколько экстремумов функции.
Теория катастроф сосредоточивает внимание на тех формах уравнения (12.2), которые являются структурно стабильными. Функция вида (12.2) с некоторыми  возможно равными нулю называется структурно стабильной, если количество и характер экстремумов этой функции не меняется, когда некоторые из этих
возможно равными нулю называется структурно стабильной, если количество и характер экстремумов этой функции не меняется, когда некоторые из этих  меняют значения. Отметим, что это определение вводится на функциональном уровне, поэтому, динамическая система является структурно стабильной, если ее кривые решений топологически эквивалентны, когда параметры изменяются.
меняют значения. Отметим, что это определение вводится на функциональном уровне, поэтому, динамическая система является структурно стабильной, если ее кривые решений топологически эквивалентны, когда параметры изменяются.
К примеру, выражение  не является структурно стабильным, так как
не является структурно стабильным, так как  имеет дополнительный экстремум. Можно показать, что для
имеет дополнительный экстремум. Можно показать, что для  полином
полином  является структурно стабильным. Эта структурно стабильная форма полинома (12.2) для заданного
является структурно стабильным. Эта структурно стабильная форма полинома (12.2) для заданного  называется универсальной разверткой для
называется универсальной разверткой для  . Количество отличных от нуля параметров, которое необходимо чтобы «стабилизировать»
. Количество отличных от нуля параметров, которое необходимо чтобы «стабилизировать»  для заданного
для заданного  , называется соразмерностью развертки, например
, называется соразмерностью развертки, например  имеет соразмерность 2.
имеет соразмерность 2.
Теория катастроф доказывает, что для соразмерности  существует точно семь различных универсальных разверток, а именно четыре развертки для одноразмерного случая (12.2) и три развертки для трехмерного случая. Эти основные результаты были получены Рене Томом (Thom) и представлены в его классификационной теореме (1977), в которой универсальные развертки носят название «элементарные катастрофы». Таблица 12.1 показывает эти семь простейших универсальных разверток с соразмерностью
существует точно семь различных универсальных разверток, а именно четыре развертки для одноразмерного случая (12.2) и три развертки для трехмерного случая. Эти основные результаты были получены Рене Томом (Thom) и представлены в его классификационной теореме (1977), в которой универсальные развертки носят название «элементарные катастрофы». Таблица 12.1 показывает эти семь простейших универсальных разверток с соразмерностью  вместе с их названиями.
вместе с их названиями.
Таблица 12.1
Универсальные развертки с соразмерностью £ 4
| Развертка
| Соразмерность
| Название
|

| 1
| складка
|

| 2
| сборка (точка возврата)
|

| 3
| ласточкин хвост
|

| 4
| бабочка
|

| 3
| сферический эллипс
|
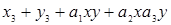
| 3
| гиперболический эллипс
|
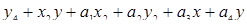
| 4
| параболический эллипс
|
Для того чтобы продемонстрировать влияние универсальных разверток на поведение динамических систем рассмотрим систему:
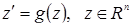 . (12.3)
. (12.3)
Предположим, что переменные могут быть разделены на «быстрые» и «медленные» переменные. К примеру, пусть 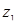 будет чрезвычайно быстрая переменная. В этом случае остальные переменные
будет чрезвычайно быстрая переменная. В этом случае остальные переменные  могут интерпретироваться как «параметры», которые изменяются очень медленно. Переменная
могут интерпретироваться как «параметры», которые изменяются очень медленно. Переменная 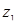 немедленно реагирует на отклонение от равновесия и изменяется неограниченно быстро к направлению своего равновесия, будучи из него выведена. Следовательно,
немедленно реагирует на отклонение от равновесия и изменяется неограниченно быстро к направлению своего равновесия, будучи из него выведена. Следовательно,
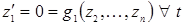 . (12.4)
. (12.4)
Уравнение  описывает
описывает 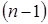 -размерное множество в
-размерное множество в 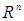 . В литературе по теории катастроф можно заметить, что это множество является поверхностью равновесия. Ее смысл заключается в том, что при
. В литературе по теории катастроф можно заметить, что это множество является поверхностью равновесия. Ее смысл заключается в том, что при 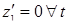 развитие системы описывается
развитие системы описывается 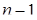 оставшимися дифференциальными уравнениями для
оставшимися дифференциальными уравнениями для 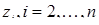 .
.
Введем новые обозначения 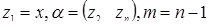 . Уравнение (12.4) может быть перезаписано в виде:
. Уравнение (12.4) может быть перезаписано в виде:
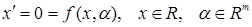 .
.
Предположим, что существует функция 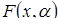 , такая что
, такая что 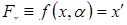 . Динамическая система, получаемая из такой функции
. Динамическая система, получаемая из такой функции 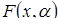 , называется градиентной системой. Теория катастроф имеет дело с динамическими системами
, называется градиентной системой. Теория катастроф имеет дело с динамическими системами 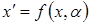 , для которых
, для которых 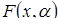 идентично членам семейства структурно стабильных универсальных разверток
идентично членам семейства структурно стабильных универсальных разверток 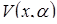 . Другими словами, она концентрирует свое внимание на тех поверхностях равновесия, которые могут быть интерпретированы, как первая производная универсальных разверток, то есть
. Другими словами, она концентрирует свое внимание на тех поверхностях равновесия, которые могут быть интерпретированы, как первая производная универсальных разверток, то есть 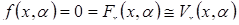 .
.
Свойства этих специфических поверхностей равновесия могут быть описаны при изучении их множеств сингулярности и бифуркационного множества. Множество сингулярности 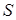 определяется как
определяется как
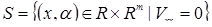 , (12.5)
, (12.5)
то есть множество всех 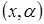 , для которых вторая производная развертки (в многомерном случае детерминант матрицы вторых производных) равна нулю. Геометрически множество сингулярности состоит из комбинации параметров, для которых поверхность равновесия является касательной к направлению переменной
, для которых вторая производная развертки (в многомерном случае детерминант матрицы вторых производных) равна нулю. Геометрически множество сингулярности состоит из комбинации параметров, для которых поверхность равновесия является касательной к направлению переменной 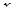 . Проекция множества сингулярности на параметрическое пространство называется бифуркационным множеством
. Проекция множества сингулярности на параметрическое пространство называется бифуркационным множеством 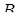 :
:
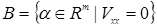 .
.
Динамическое поведение при катастрофе складки – простейшем типе катастроф, аналогично поведению непрерывной системы, в которой происходит бифуркация складки: при 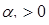 не существует никакого равновесия в рассматриваемой динамической системе. При
не существует никакого равновесия в рассматриваемой динамической системе. При 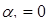 возникает бифуркация в
возникает бифуркация в 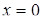 , такая, что при
, такая, что при 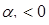 существуют ветви стабильного и нестабильного равновесия. Поэтому далее будем рассматривать катастрофу с точкой возврата.
существуют ветви стабильного и нестабильного равновесия. Поэтому далее будем рассматривать катастрофу с точкой возврата.
Развертка для катастрофы с точкой возврата
 (12.6)
(12.6)
имеет поверхность равновесия
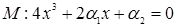 , (12.7)
, (12.7)
и множество сингулярности
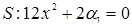 . (12.8)
. (12.8)
Бифуркационное множество может быть получено исключением 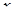 из
из 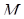 и
и 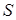 , дающее:
, дающее:
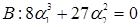 . (12.9)
. (12.9)
Кстати, формула (12.9) в точности совпадает с формулой дискриминанта уравнения поверхности равновесия (12.7). Отсюда следует, что (12.7) имеет три действительных корня, которые все совпадают, если 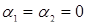 , или два из них совпадают, если
, или два из них совпадают, если 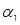 и
и 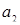 различны. Поскольку развертка (12.6) является объектом в четырехмерном пространстве
различны. Поскольку развертка (12.6) является объектом в четырехмерном пространстве 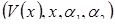 , геометрическое представление катастрофы с точкой возврата должно начинаться с поверхности равновесия (см. рис. 12.1)
, геометрическое представление катастрофы с точкой возврата должно начинаться с поверхности равновесия (см. рис. 12.1)
Термин «точка возврата» является очевидным следствием формы бифуркационного множества. Переменная состояния всегда находится на вершине поверхности равновесия. Становится очевидно, что как только параметры изменятся так, что переменная состояния достигнет множества сингулярности в точке 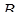 (см. рис. 12.2) после перемещения по верхней части поверхности, переменная
(см. рис. 12.2) после перемещения по верхней части поверхности, переменная 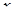 перескакивает вниз на нижнюю часть
перескакивает вниз на нижнюю часть 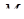 (рис. 12.1).
(рис. 12.1).
Если траектория изменения параметров 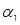 и
и 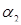 такова, что происходит движение из точки
такова, что происходит движение из точки 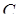 в нижней плоскости в точку
в нижней плоскости в точку 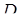 , то далее из
, то далее из 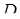 происходит скачок в верхнюю плоскость, при котором она вновь принадлежит множеству сингулярности. Таким образом, процесс бифуркации происходит каждый раз, когда траектория пересекает бифуркационное множество.
происходит скачок в верхнюю плоскость, при котором она вновь принадлежит множеству сингулярности. Таким образом, процесс бифуркации происходит каждый раз, когда траектория пересекает бифуркационное множество.
Траектория 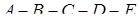 изображена на рис. 12.1 исходит из существенного предположения, что
изображена на рис. 12.1 исходит из существенного предположения, что 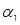 изменяется очень медленно. Когда
изменяется очень медленно. Когда 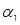 в состоянии изменяться с большей скоростью, могут возникать и другие сценарии поведения в этой модели. Предположим, к примеру, что система находится в точке
в состоянии изменяться с большей скоростью, могут возникать и другие сценарии поведения в этой модели. Предположим, к примеру, что система находится в точке 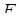 . Возможно, что траектория на поверхности сначала совершает движение в направлении точки
. Возможно, что траектория на поверхности сначала совершает движение в направлении точки 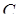 , а далее – как это описывалось ранее. В этом случае никакой бифуркации не происходит, так как бифуркационное множество ни разу не пересекалось. Какой именно путь переменная пройдет, конечно же, определяется конкретной формой уравнений (12.3).
, а далее – как это описывалось ранее. В этом случае никакой бифуркации не происходит, так как бифуркационное множество ни разу не пересекалось. Какой именно путь переменная пройдет, конечно же, определяется конкретной формой уравнений (12.3).
Прочие элементарные катастрофы вообще-то более сложно проиллюстрировать. Они требуют закрепления на постоянном уровне одной или нескольких переменных, для того чтобы представить их графически. Поскольку большинство экономических приложений теории катастроф сосредоточиваются на геометрических аспектах, то кажется, что катастрофы более высоких порядков не имеют прямого отношения к экономике.
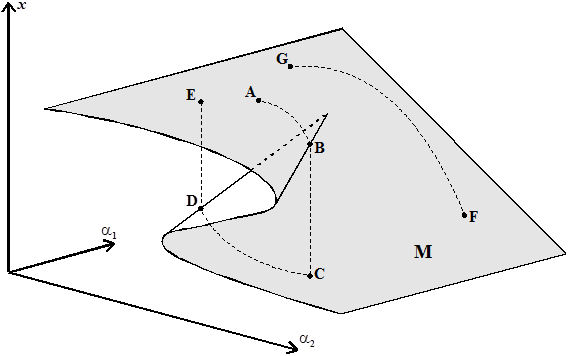
Рисунок 12.1. Катастрофа сборки.
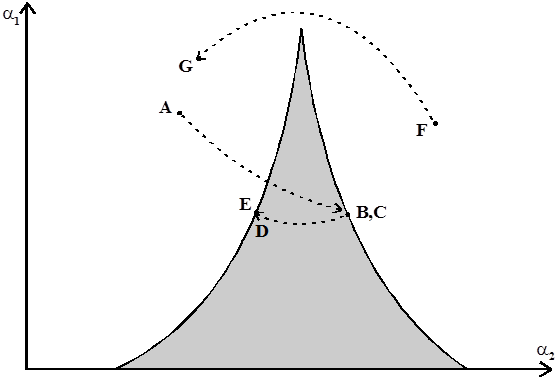
Рисунок 12.2. Бифуркационное множество катастрофе сборки.
Как уже обсуждалось ранее, теория катастроф заслуживает названия «теория» весьма условно. Конечно, теория катастроф дает информацию о возможных типах поведения в динамической системе, но, вообще говоря, не дает ответа на вопрос что именно случится в четко определенной системе. Движение по поверхности равновесия зависит от медленных переменных, и без исчерпывающей информации об этой медленной динамике невозможно ничего сказать о динамике переменных состояния. Однако, поскольку динамическая система точно описана, не имеет смысла обращаться к теории катастроф, поскольку поведение системы может быть более легко изучено при помощи других средств. Теория катастроф поэтому должна представляться как эвристический инструмент для изучения проблем, для которых слишком мало известно о формальной динамике системы для построения дескриптивной модели.
Теория катастроф применялась для изучения многих экономических проблем, включая поведение правительства, крах фондовых бирж (Зиман, 1977), плавную динамику (Мэлинвод, 1977), макромодель с нормированием (Блэд, 1981), возможную структурную нестабильность предположения Вальраса (Бирченхолл, 1979), и т.п. Далее будут рассмотрены два наиболее характерных примера применения теории катастроф в экономике.



 -размерным вектором
-размерным вектором 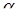 :
: . (12.1)
. (12.1) будет аналитической функцией, которую можно записать в виде многочлена:
будет аналитической функцией, которую можно записать в виде многочлена: , (12.2)
, (12.2) возможно равными нулю.
возможно равными нулю. график многочлена имеет различную форму, если некоторые параметры исчезают. К примеру рассмотрим случай, когда
график многочлена имеет различную форму, если некоторые параметры исчезают. К примеру рассмотрим случай, когда  с
с  ,
, 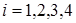 . График
. График 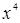 достаточно сильно отличается от графика
достаточно сильно отличается от графика  . В зависимости от количества исчезающих параметров i, могут возникнуть один или несколько экстремумов функции.
. В зависимости от количества исчезающих параметров i, могут возникнуть один или несколько экстремумов функции. не является структурно стабильным, так как
не является структурно стабильным, так как  имеет дополнительный экстремум. Можно показать, что для
имеет дополнительный экстремум. Можно показать, что для  полином
полином  является структурно стабильным. Эта структурно стабильная форма полинома (12.2) для заданного
является структурно стабильным. Эта структурно стабильная форма полинома (12.2) для заданного  называется универсальной разверткой для
называется универсальной разверткой для  . Количество отличных от нуля параметров, которое необходимо чтобы «стабилизировать»
. Количество отличных от нуля параметров, которое необходимо чтобы «стабилизировать»  для заданного
для заданного  имеет соразмерность 2.
имеет соразмерность 2. существует точно семь различных универсальных разверток, а именно четыре развертки для одноразмерного случая (12.2) и три развертки для трехмерного случая. Эти основные результаты были получены Рене Томом (Thom) и представлены в его классификационной теореме (1977), в которой универсальные развертки носят название «элементарные катастрофы». Таблица 12.1 показывает эти семь простейших универсальных разверток с соразмерностью
существует точно семь различных универсальных разверток, а именно четыре развертки для одноразмерного случая (12.2) и три развертки для трехмерного случая. Эти основные результаты были получены Рене Томом (Thom) и представлены в его классификационной теореме (1977), в которой универсальные развертки носят название «элементарные катастрофы». Таблица 12.1 показывает эти семь простейших универсальных разверток с соразмерностью 




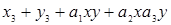
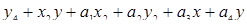
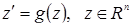 . (12.3)
. (12.3)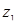 будет чрезвычайно быстрая переменная. В этом случае остальные переменные
будет чрезвычайно быстрая переменная. В этом случае остальные переменные  могут интерпретироваться как «параметры», которые изменяются очень медленно. Переменная
могут интерпретироваться как «параметры», которые изменяются очень медленно. Переменная 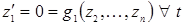 . (12.4)
. (12.4) описывает
описывает 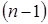 -размерное множество в
-размерное множество в 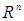 . В литературе по теории катастроф можно заметить, что это множество является поверхностью равновесия. Ее смысл заключается в том, что при
. В литературе по теории катастроф можно заметить, что это множество является поверхностью равновесия. Ее смысл заключается в том, что при 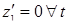 развитие системы описывается
развитие системы описывается 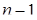 оставшимися дифференциальными уравнениями для
оставшимися дифференциальными уравнениями для 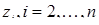 .
.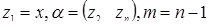 . Уравнение (12.4) может быть перезаписано в виде:
. Уравнение (12.4) может быть перезаписано в виде: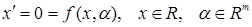 .
.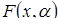 , такая что
, такая что 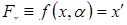 . Динамическая система, получаемая из такой функции
. Динамическая система, получаемая из такой функции 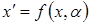 , для которых
, для которых 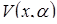 . Другими словами, она концентрирует свое внимание на тех поверхностях равновесия, которые могут быть интерпретированы, как первая производная универсальных разверток, то есть
. Другими словами, она концентрирует свое внимание на тех поверхностях равновесия, которые могут быть интерпретированы, как первая производная универсальных разверток, то есть 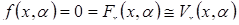 .
.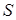 определяется как
определяется как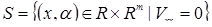 , (12.5)
, (12.5)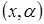 , для которых вторая производная развертки (в многомерном случае детерминант матрицы вторых производных) равна нулю. Геометрически множество сингулярности состоит из комбинации параметров, для которых поверхность равновесия является касательной к направлению переменной
, для которых вторая производная развертки (в многомерном случае детерминант матрицы вторых производных) равна нулю. Геометрически множество сингулярности состоит из комбинации параметров, для которых поверхность равновесия является касательной к направлению переменной 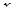 . Проекция множества сингулярности на параметрическое пространство называется бифуркационным множеством
. Проекция множества сингулярности на параметрическое пространство называется бифуркационным множеством 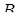 :
: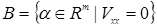 .
.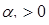 не существует никакого равновесия в рассматриваемой динамической системе. При
не существует никакого равновесия в рассматриваемой динамической системе. При 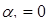 возникает бифуркация в
возникает бифуркация в 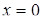 , такая, что при
, такая, что при 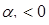 существуют ветви стабильного и нестабильного равновесия. Поэтому далее будем рассматривать катастрофу с точкой возврата.
существуют ветви стабильного и нестабильного равновесия. Поэтому далее будем рассматривать катастрофу с точкой возврата. (12.6)
(12.6)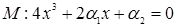 , (12.7)
, (12.7)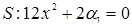 . (12.8)
. (12.8)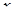 из
из 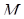 и
и 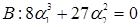 . (12.9)
. (12.9)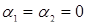 , или два из них совпадают, если
, или два из них совпадают, если 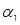 и
и 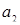 различны. Поскольку развертка (12.6) является объектом в четырехмерном пространстве
различны. Поскольку развертка (12.6) является объектом в четырехмерном пространстве 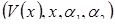 , геометрическое представление катастрофы с точкой возврата должно начинаться с поверхности равновесия (см. рис. 12.1)
, геометрическое представление катастрофы с точкой возврата должно начинаться с поверхности равновесия (см. рис. 12.1)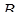 (см. рис. 12.2) после перемещения по верхней части поверхности, переменная
(см. рис. 12.2) после перемещения по верхней части поверхности, переменная 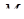 (рис. 12.1).
(рис. 12.1).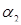 такова, что происходит движение из точки
такова, что происходит движение из точки 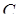 в нижней плоскости в точку
в нижней плоскости в точку 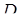 , то далее из
, то далее из 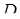 происходит скачок в верхнюю плоскость, при котором она вновь принадлежит множеству сингулярности. Таким образом, процесс бифуркации происходит каждый раз, когда траектория пересекает бифуркационное множество.
происходит скачок в верхнюю плоскость, при котором она вновь принадлежит множеству сингулярности. Таким образом, процесс бифуркации происходит каждый раз, когда траектория пересекает бифуркационное множество.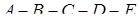 изображена на рис. 12.1 исходит из существенного предположения, что
изображена на рис. 12.1 исходит из существенного предположения, что  . Возможно, что траектория на поверхности сначала совершает движение в направлении точки
. Возможно, что траектория на поверхности сначала совершает движение в направлении точки 




