

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
При всем многообразии подходов к моделированию экономического роста, большинство современных исследований этого вопроса основываются на модели Солоу (Solow, 1956 г).
Рассмотрим процесс экономического роста, при котором возможна продолжительная полная занятость, и поэтому ситуация стабильна.
В соответствии с первым вопросом (существование), очевидно, что в предположении, что технический прогресс отсутствует, доход и рабочая сила должны увеличиваться с одним и тем же (пропорциональным) темпом роста. Это так называемая устойчивая (или сбалансированная) модель роста, иными словами, это модель, в которой все переменные растут с одним темпом роста так, что этот темп постоянен. В качестве отправной точки возьмем фундаментальное отношение:
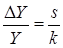 , (6.20)
, (6.20)
где 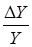 (то есть
(то есть 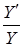 в непрерывном случае) – темп роста дохода, а
в непрерывном случае) – темп роста дохода, а 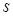 и
и 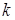 – как обычно, средняя (или предельная) склонность к накоплению и средняя (или предельная) капиталоемкость. Это утверждение легко доказывается:
– как обычно, средняя (или предельная) склонность к накоплению и средняя (или предельная) капиталоемкость. Это утверждение легко доказывается:
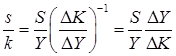 ,
,
и, поскольку 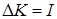 (без учета обесценивания), и в точке равновесия
(без учета обесценивания), и в точке равновесия 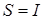 , следовательно,
, следовательно, 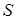 и
и 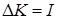 сокращаются, то есть
сокращаются, то есть 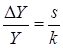 . В непрерывном случае
. В непрерывном случае 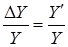 и
и 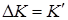 .
.
В предположении, что население растет с постоянным (пропорциональным темпом роста), скажем 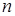 , и что рабочая сила является постоянной составляющей населения, и, таким образом, растет с тем же темпом роста
, и что рабочая сила является постоянной составляющей населения, и, таким образом, растет с тем же темпом роста 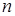 , условие существования роста полной занятости:
, условие существования роста полной занятости:
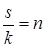 . (6.21)
. (6.21)
В общем случае, если 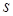 ,
, 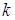 и
и 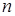 – заданные константы, это равенство может быть чисто случайным, и нельзя ожидать, что оно будет выполняться. Вместо этого, если предположить, что
– заданные константы, это равенство может быть чисто случайным, и нельзя ожидать, что оно будет выполняться. Вместо этого, если предположить, что 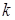 – переменная, принципиально возможно удовлетворить это равенство, предусматривающее, что
– переменная, принципиально возможно удовлетворить это равенство, предусматривающее, что 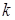 может оказывать влияние на
может оказывать влияние на 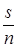 .
.
|
|
6.2.1. Существование равновесного роста
Неоклассическая агрегированная модель роста в своем наипростейшем виде предполагает, что функция производства является однородной первого порядка (с обычными свойством положительной, но убывающей предельной производительности) и, что эта функция допускает бесконечную заменяемость между трудом и капиталом. Под «бесконечной» заменяемостью мы понимаем, что для производства данного уровня продукции, любого количества – от нуля (включая или исключая) до бесконечности, капитал может быть (эффективно) использован, очевидно с использованием соответствующего количества труда. Это предположение вводится для того, чтобы позволить капиталоемкости принимать любое (неотрицательное) значение. Если оно не будет выполняться, то может случиться, что уровень капиталоемкости, необходимый для того, чтобы уравновесить 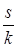 и
и 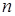 , не сможет быть достигнут посредством технологии, описываемой производственной функцией.
, не сможет быть достигнут посредством технологии, описываемой производственной функцией.
В этом случае всегда можно уравновесить 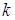 и
и 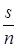 . Со статической точки зрения, это означает, что необходимо определить уровень капиталовооруженности, дающий такой уровень производительности труда, чтобы капиталоемкость находилась на желаемом уровне. Формально, задавая производственную функцию в виде
. Со статической точки зрения, это означает, что необходимо определить уровень капиталовооруженности, дающий такой уровень производительности труда, чтобы капиталоемкость находилась на желаемом уровне. Формально, задавая производственную функцию в виде
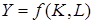 , (6.22)
, (6.22)
можно использовать свойство однородности первого порядка, для ее преобразования к виду интенсивностей:
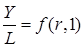 , (6.23)
, (6.23)
где 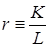 .
.
Предположение о бесконечной заменяемости означает выполнение следующих условий:
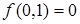 ,
, 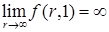 , (6.24)
, (6.24)
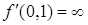 ,
, 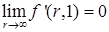 .
.
Условия (6.24) обычно называют условия Инэда (Inada, 1963).
Теперь
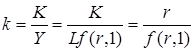 , (6.25)
, (6.25)
так, что требуемое количество капитала на единицу труда получают, решая уравнение
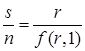 ,
,
которое можно переписать в виде:
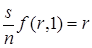 , (6.26)
, (6.26)
или
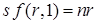 . (6.27)
. (6.27)
Простая графическая интерпретация уравнения (6.27) дана на рис. 6.2.
|
|
Если производственная функция является доброкачественной, что означает, что условия (6.24) выполняются, пересечение, причем единственное, существует. Точка A дает требуемое количество капитала на единицу труда. Легко видно, что этот объем в точности совпадает с тем, который дает уровень капиталоемкости sn. По определению:
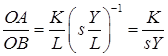 .
.
Геометрически:
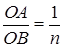
и уравнивая два результата, получим:
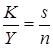 .
.
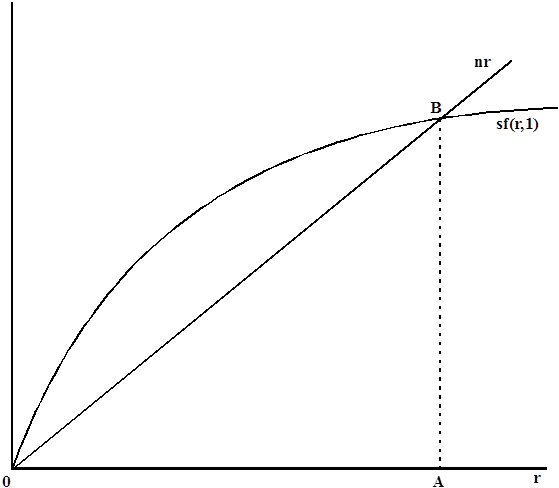
Рисунок 6.2. Неоклассическая модель роста.
6.2.2. Стабильность равновесного роста
Перейдем к вопросу о стабильности. Простейшие уравнения модели, уже были представлены:
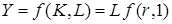 , (6.28)
, (6.28)
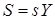 , (6.29)
, (6.29)
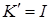 , (6.30)
, (6.30)
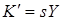 , (6.31)
, (6.31)
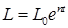 . (6.32)
. (6.32)
Уравнение (6.31) предполагает, что 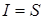 (как ожидаемое значение) и уравнение (6.32) предполагает, что существует полная занятость. Определим
(как ожидаемое значение) и уравнение (6.32) предполагает, что существует полная занятость. Определим 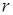 :
:
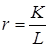 ,
,
откуда
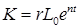 . (6.33)
. (6.33)
Поскольку уравнение (6.33) является тождеством, производные обоих его частей также равны (для уравнений это в общем не является истинным). Следовательно, можно продифференцировать обе части по времени. Получим:
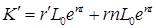 ,
,
откуда, используя уравнения (6.31), (6.28) и (6.32), получим:
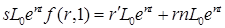 .
.
Множитель 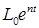 сокращается, откуда получаем:
сокращается, откуда получаем:
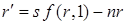 , (6.34)
, (6.34)
которое является основным динамическим уравнением этой модели.
Легко видно, что если производственная функция доброкачественна, точка равновесия стабильна. Прежде всего, отметим, что если наложить ограничение на то, что 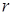 находится в точке равновесия, то есть что
находится в точке равновесия, то есть что 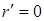 , то из уравнения (6.34) получим уравнение (6.27), которое уже рассматривалось ранее.
, то из уравнения (6.34) получим уравнение (6.27), которое уже рассматривалось ранее.
Рассмотрим теперь рис. 6.2: слева (справа) от точки 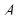 функция
функция 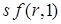 лежит выше (ниже) функции
лежит выше (ниже) функции 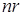 , то есть
, то есть 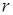 увеличивается (уменьшается) в соответствии с выражением
увеличивается (уменьшается) в соответствии с выражением 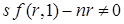 . Из этого следует, что слева (справа) от точки
. Из этого следует, что слева (справа) от точки 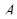 производная
производная 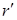 – положительна (отрицательна), то есть
– положительна (отрицательна), то есть 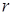 увеличивается (уменьшается) в соответствии с тем меньше (больше) ли она своего равновесного значения. Это доказывает стабильность. Аналогичное объяснение может доказать нестабильность равновесия в случае, если функция
увеличивается (уменьшается) в соответствии с тем меньше (больше) ли она своего равновесного значения. Это доказывает стабильность. Аналогичное объяснение может доказать нестабильность равновесия в случае, если функция 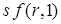 пересекает функцию
пересекает функцию  снизу.
снизу.
Для анализа специфических случаев, следует лишь подставить специфическую функцию вместо функции 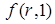 . К примеру, задавая хорошо известную производственную функцию Кобба – Дугласа (Cobb - Douglas)
. К примеру, задавая хорошо известную производственную функцию Кобба – Дугласа (Cobb - Douglas) 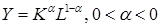 , получим
, получим 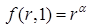 , так, что уравнение (6.34) принимает вид:
, так, что уравнение (6.34) принимает вид:
|
|
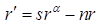 . (6.35)
. (6.35)
Уравнение (6.35), несмотря на первый порядок, является нелинейным, поскольку 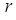 возводится в степень
возводится в степень 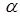 . Однако, оно может быть приведено к линейному виду посредством простого преобразования. Введем новую переменную,
. Однако, оно может быть приведено к линейному виду посредством простого преобразования. Введем новую переменную, 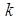 , связанную с
, связанную с 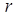 следующим выражением:
следующим выражением:
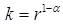 . (6.36)
. (6.36)
Отметим, что математические преобразования, являющиеся основным методом решения дифференциальных уравнений указанного вида, также имеют и экономическую интерпретацию:
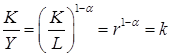 , (6.37)
, (6.37)
то есть математическое преобразование просто означает переход от капиталовооруженности к капиталоемкости, которая как раз и является неизвестной, и ее следует определить.
Дифференцируя уравнение (6.36) относительно времени, получим:
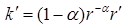 ,
,
то есть
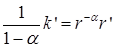 . (6.38)
. (6.38)
Умножим обе части уравнения (6.35) на 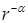 :
:
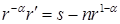 ,
,
и с использованием уравнений (6.36) и (6.38), получим:
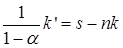 ,
,
то есть
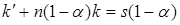 , (6.39)
, (6.39)
которое линейно относительно 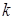 (и с постоянными коэффициентами).
(и с постоянными коэффициентами).
Общее решение однородной части (6.39):
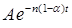 ,
,
а частное решение находится, в предположении, что 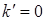 :
:
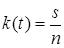 ,
,
таким образом, общее решение (6.39):
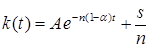 . (6.40)
. (6.40)
Полагая, что 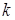 имеет известное значение, скажем
имеет известное значение, скажем 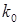 для момента времени
для момента времени 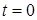 , из (6.40) получим следующее выражение:
, из (6.40) получим следующее выражение:
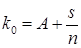 ,
,
откуда
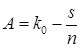 ,
,
и
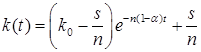 . (6.41)
. (6.41)
Поскольку 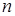 и
и 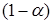 – положительны, величина
– положительны, величина 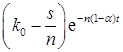 стремится к нулю при увеличении
стремится к нулю при увеличении 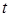 , а
, а 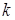 стремится к своему равновесному значению
стремится к своему равновесному значению 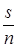 . Это, собственно, и есть искомый результат. Интервал между
. Это, собственно, и есть искомый результат. Интервал между 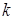 и устойчивым состоянием исчезает с постоянным темпом:
и устойчивым состоянием исчезает с постоянным темпом:
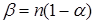 , (6.42)
, (6.42)
где 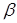 – коэффициент сходимости.
– коэффициент сходимости.
Чтобы закончить исследование вернемся к первоначальной переменной 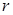 . Из уравнения (6.36) получим обратное преобразование:
. Из уравнения (6.36) получим обратное преобразование:
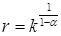 , (6.43)
, (6.43)
и применим его к уравнению (6.41):
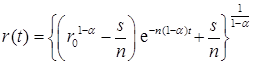 , (6.44)
, (6.44)
где 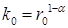 . Следовательно,
. Следовательно, 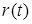 стремится к своему равновесному значению
стремится к своему равновесному значению 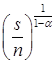 .
.
Уровень производства 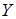 , разумеется, стремится к своему состоянию стабильности с темпом роста
, разумеется, стремится к своему состоянию стабильности с темпом роста 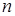 . Фактически, из производственной функции имеем
. Фактически, из производственной функции имеем 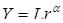 , откуда
, откуда 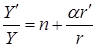 . Поскольку уравнение (6.35) дает
. Поскольку уравнение (6.35) дает 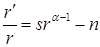 , используя (6.44) легко видеть, что
, используя (6.44) легко видеть, что 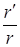 сходится к нулю, поскольку
сходится к нулю, поскольку 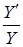 сходится к
сходится к 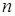 .
.
|
|
|
|
|

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!