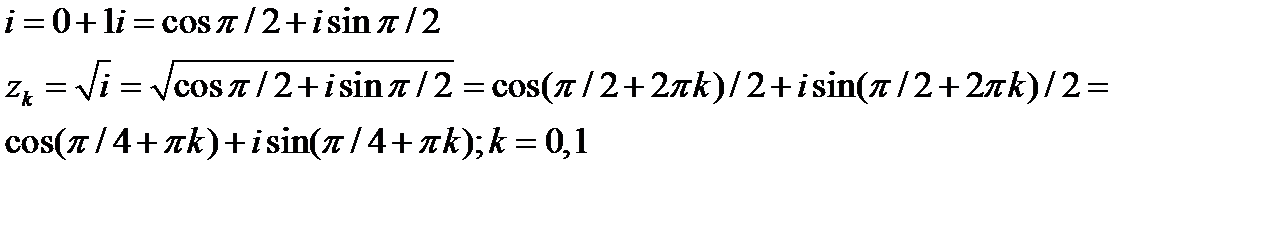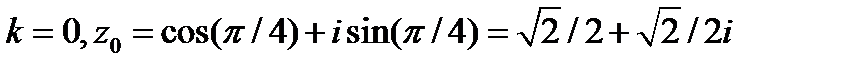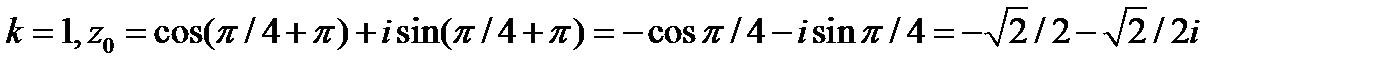1. Числовой ряд.
Пусть задана числовая последовательность 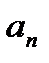 ,
, 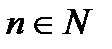 . Тогда последовательность (1)
. Тогда последовательность (1) 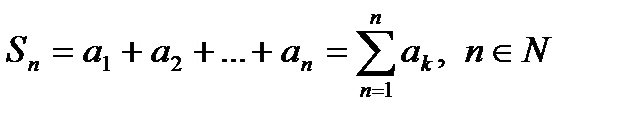 называется числовым рядом и обозначается,
называется числовым рядом и обозначается, 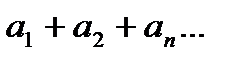 или
или 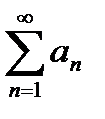 (2) числа
(2) числа 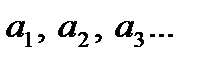 называется членами ряда (2), соответственно первым, вторым, … членами ряда.
называется членами ряда (2), соответственно первым, вторым, … членами ряда.
Суммы 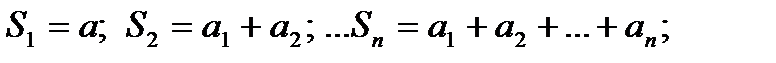 называются частичными суммами ряда (2)
называются частичными суммами ряда (2)
Ряд 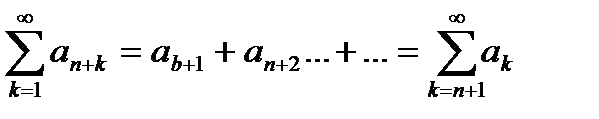 (3) называется
(3) называется 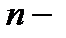 остатком ряда (2). Отметим, что у ряда (3) первым членом является
остатком ряда (2). Отметим, что у ряда (3) первым членом является 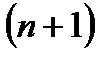 член исходного ряда (2) и к-ый член ряда (3) равен
член исходного ряда (2) и к-ый член ряда (3) равен 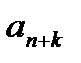 .
.
Ряд называется сходящимся, если последовательность его частичных сумм сходится.
Если последовательность частичных сумм расходится, то он называется расходящимся.
То если существует предел 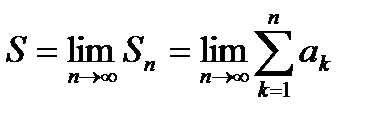 , то ряд называется сходящимся, а число, а число
, то ряд называется сходящимся, а число, а число 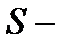 суммой сходящегося ряда.
суммой сходящегося ряда.
Если частичная сумма 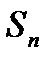 ряда (2) при неограниченном возрастании n не имеет конечного предела, то ряд называется расходящимся.
ряда (2) при неограниченном возрастании n не имеет конечного предела, то ряд называется расходящимся.
Разность 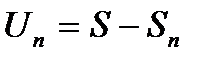 называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т. е.
называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т. е. 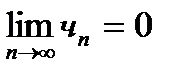 и наоборот, если остаток стремится к нулю, то ряд сходится.
и наоборот, если остаток стремится к нулю, то ряд сходится.
2. Геометрический ряд
Геометрический ряд, это ряд, составленный из членов геометрической прогрессии 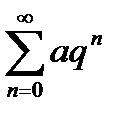
а) Если 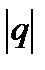 < 1 то,
< 1 то, 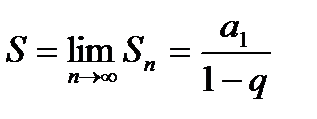 т. е. ряд сходится
т. е. ряд сходится
б) Если 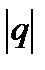 > 1 то,
> 1 то, 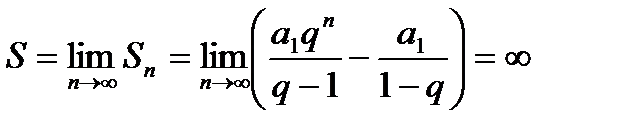 т. е. ряд расходится
т. е. ряд расходится
в) Если 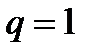 то,
то, 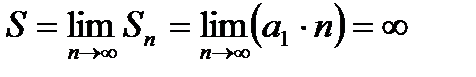 т. е. ряд расходится
т. е. ряд расходится
г) Если 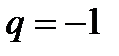 то, ряд расходится
то, ряд расходится
3. Гармонический ряд
Ряд вида 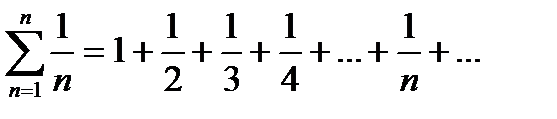 называется гармоническим
называется гармоническим
1) Необходимый признак сходимости ряда
Ряд 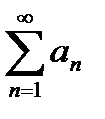 может сходиться только при условии, что его общий член
может сходиться только при условии, что его общий член 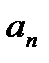 при неограниченном увеличении номера,
при неограниченном увеличении номера, 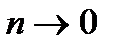 т. е.
т. е. 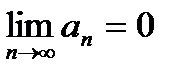 если
если 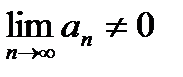 , то ряд
, то ряд 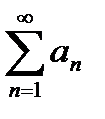 расходится это достаточный признак расходимости ряда
расходится это достаточный признак расходимости ряда
2) Достаточный признак сходимости
а) Признак сравнения с положительными членами.
Исследуемый ряд сходится, если его члены не превосходят соответствующих членов другого заведомо расходящегося ряда. При исследовании на сходимость и расходимость по этому признаку часть используется геометрический ряд, 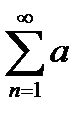 который сходится при
который сходится при 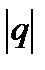 < 1 и расходится при
< 1 и расходится при 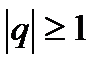 и гармонический ряд
и гармонический ряд 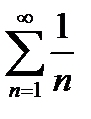 , который является расходящимся.
, который является расходящимся.
б) Признак Даламбера
Если для ряда с положительным членом 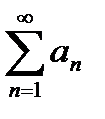 выполняется условие,
выполняется условие, 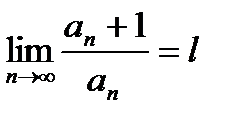 то ряд сходится при
то ряд сходится при 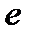 < 1 и расходится при
< 1 и расходится при 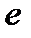 > 1. Признак Даламбера не дает ответа, если
> 1. Признак Даламбера не дает ответа, если 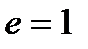 . В этом случае для исследования ряда применяется другие приемы.
. В этом случае для исследования ряда применяется другие приемы.
Найти сумму членов ряда:
а) 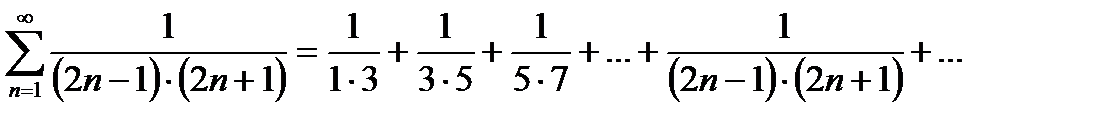
б) 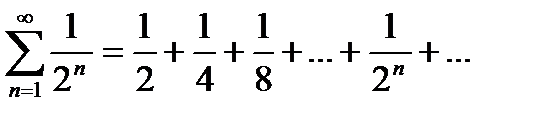
Решение: а) Найдем частичные суммы членов ряда:
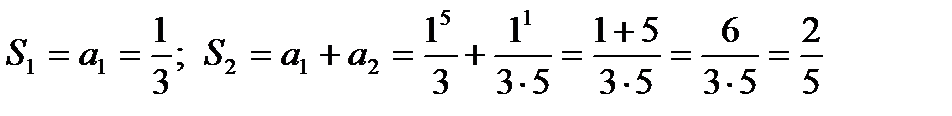
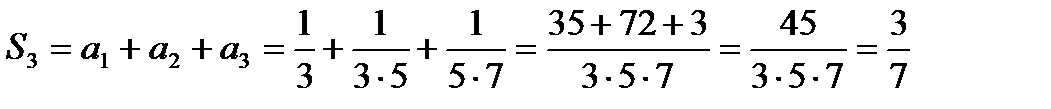
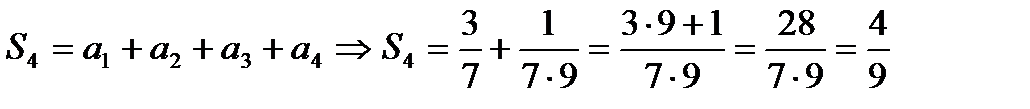
Запишем последовательность частичных сумм
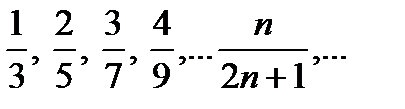
Общий член будет: 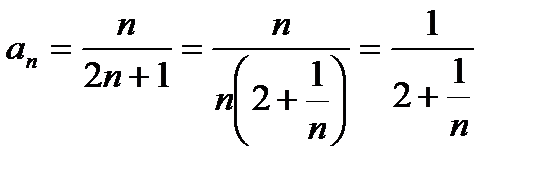
Следовательно 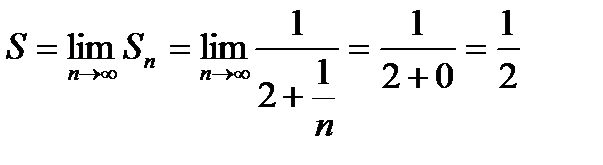
Так как 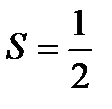 , то ряд сходится и его сумма равна
, то ряд сходится и его сумма равна 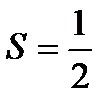
б) Найдем первый способ: частичные суммы членов ряда:
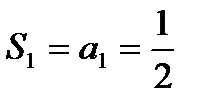
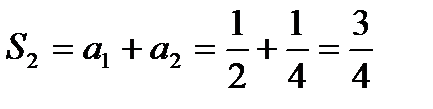
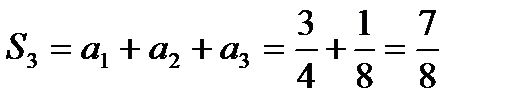
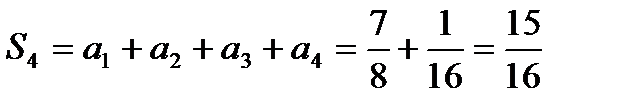 и т. д.
и т. д.
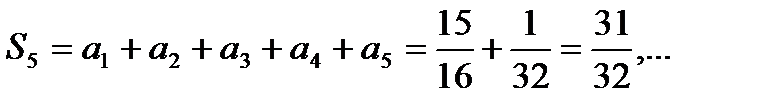
Запишем последовательность частичных сумм:
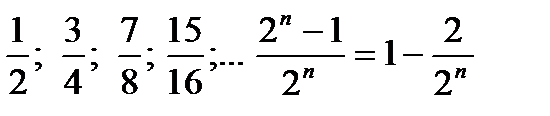
Следовательно: 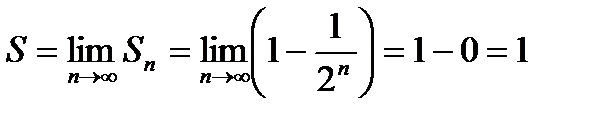
Значит, ряд сходится и его сумма равна 1
2 способ
Это бесконечно убывающая геометрическая прогрессия, которой 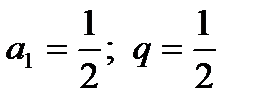 . Используя формулу
. Используя формулу 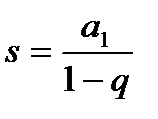 ; получим
; получим 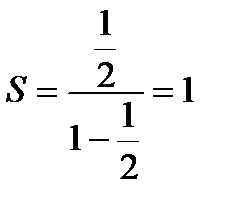 Значит ряд, сходится
Значит ряд, сходится
2.Исследовать сходимость ряда, применяя необходимый признак сходимости и признак сравнения:
а) 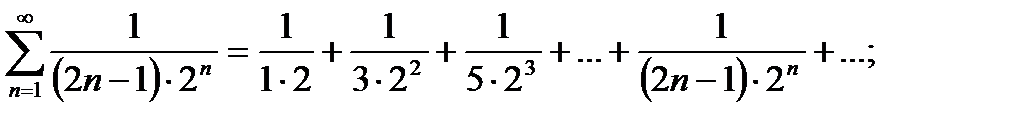
б) 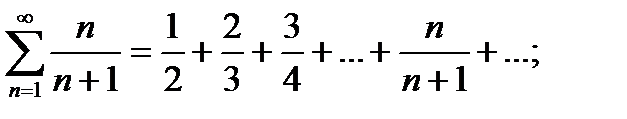
Решение:
а) Найдем 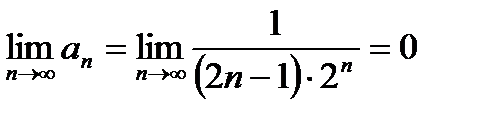
Необходимое условие выполнено. Рассмотрим достаточное условие: сравним данный ряд с геометрическим рядом.
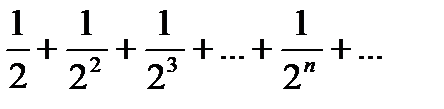 который сходится, т. к.
который сходится, т. к. 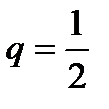 <
< 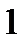
Сравнивая члены данного ряда, начиная со второго, с соответствующими членами геометрического ряда, получим неравенство:
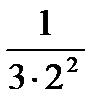 <
< 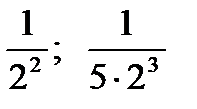 <
< 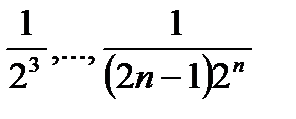 <
< 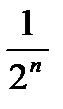 ;
;
т. е. члены данного ряда, начиная со второго, соответственно меньше членов геометрического ряда, откуда следует, что данный ряд сходится.
б) Имеем 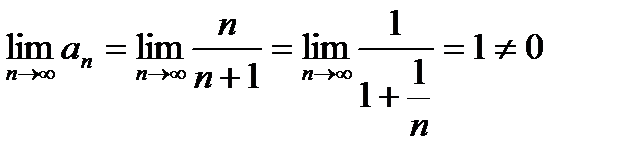
Выполняется достаточный признак расходимости ряда, следовательно, ряд расходится
3.Исследовать сходимость ряда, используя признак Даламбера:
а) 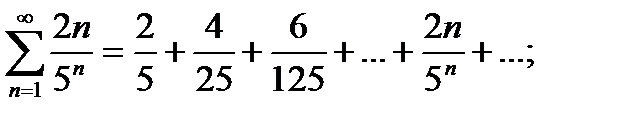
б) 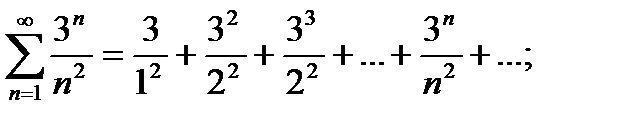
Решение: а) общий член 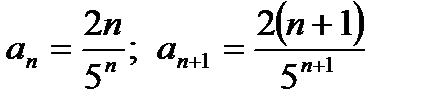
Найдем предел отношения 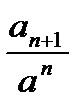 , т. е.
, т. е.
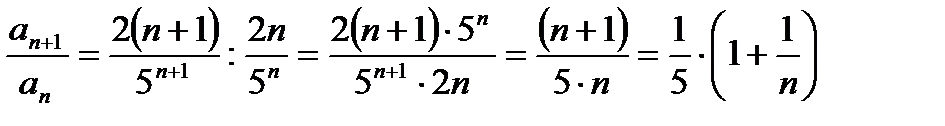
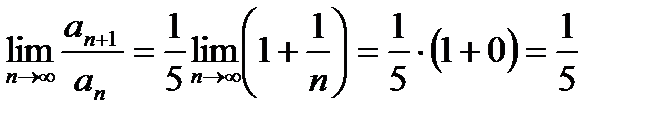 <
< 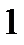
Следовательно, ряд расходится.
б) Имеем 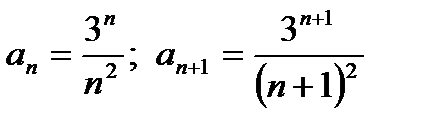
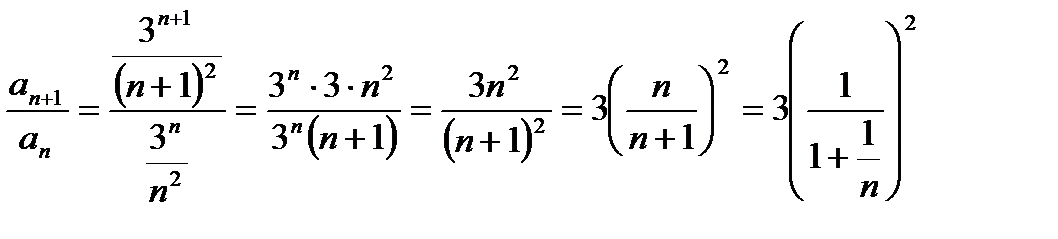
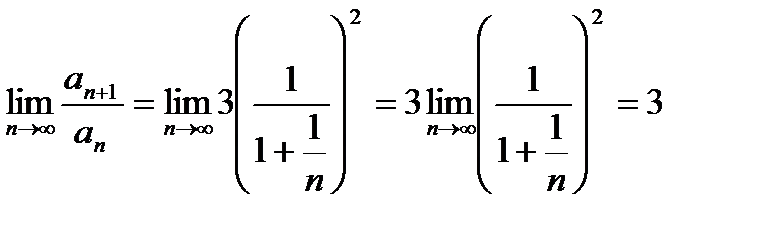 >
> 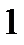 Значит, ряд расходится.
Значит, ряд расходится.
Вопросы для самопроверки:
1. Какая последовательность называется числовым рядом?
2. Как обозначаются числовой ряд?
3. Какие числа называются частичными суммами ряда?
4. Какой ряд называется промежуточным остатком ряда?
5. Если последовательность части сумм сходится, то, как называется такой ряд?
6. Если последовательность частичных сумм расходится, то, как называется такой ряд?
7. Если существует предел 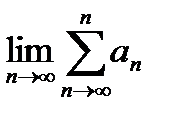 , то, как называется такой ряд?
, то, как называется такой ряд?
8. Как называется разность 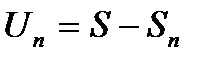
9. Если ряд сходится, то, будет, ли его остаток стремится к нулю?
10. Какой ряд называется геометрическим?
11. Какое условие, геометрический ряд сходится и при каком, условии расходятся?
12. Какой ряд называется гармоническим?
13. Если 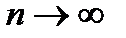 и
и 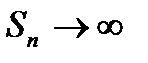 , то будет, ли гармонический ряд сходится?
, то будет, ли гармонический ряд сходится?
14. Сформулировать необходимый признак сходимости ряда.
15. Сформулировать достаточный признак сходимости ряда.
16. К какому признаку сходимости относится высказывание: исследуемый ряд расходится, если его члены превосходят соответствующие члены другого заведомо расходящиеся ряда.
17. При исследовании на сходимость по признаку, сравнения какой ряд обычно рассматривают?
18. Сформулировать признак Даламбера
19. Если выполняется условие 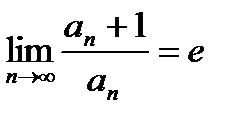 то, при каком условии ряд, сходится и при каком условии ряд расходится.
то, при каком условии ряд, сходится и при каком условии ряд расходится.
Тема 1.4. Комплексные числа
Комплексными называются числа вида 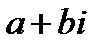 где
где 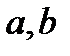 действительные числа,
действительные числа, 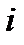 -число, определенное равенством
-число, определенное равенством 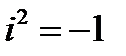 -называют мнимой единицей.
-называют мнимой единицей.
Действия сложения и умножения:
1. Два комплексных числа 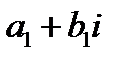 и
и 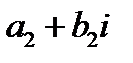 называются равными, если
называются равными, если 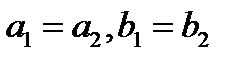
2.Суммой двух комплексных чисел 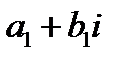 и
и 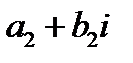 называется комплексное число
называется комплексное число
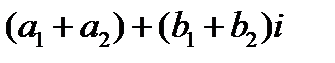
3.Произведением двух комплексных чисел 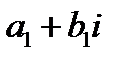 и
и 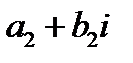 называется комплексное число
называется комплексное число
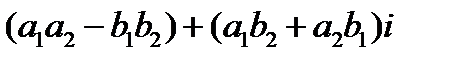
Запись комплексного числа в виде 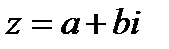 называется алгебраической формой записи комплексного числа. Действительное число
называется алгебраической формой записи комплексного числа. Действительное число 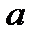 называется действительной частью комплексного числа
называется действительной частью комплексного числа 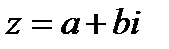 , а действительное число
, а действительное число 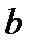 мнимой частью.
мнимой частью.
При 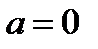 , комплексное число
, комплексное число 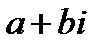 обращается в чисто мнимое число
обращается в чисто мнимое число 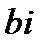 .
.
Комплексное число 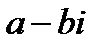 называется комплексно сопряженным с числом
называется комплексно сопряженным с числом 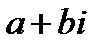 и обозначается
и обозначается 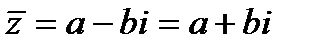
Комплексные числа вида 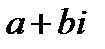 и
и 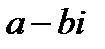 называются противоположными.
называются противоположными.
Модулем комплексного числа 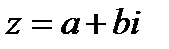 называется число
называется число 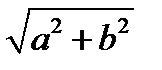 , т.е.
, т.е. 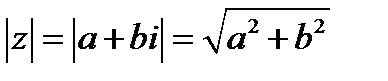 .
.
Комплексное число 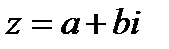 можно изображать точкой плоскости с координатами
можно изображать точкой плоскости с координатами 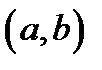
Действительное число изображается точкой оси абсцисс, которую называют действительной осью, мнимые числа-точками оси ординат, которую называют мнимой осью. Каждой точке плоскости с координатами с координатами 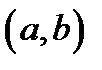 соответствует один и только один вектор с началом в точке
соответствует один и только один вектор с началом в точке 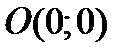 и концом в точке
и концом в точке 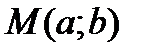 . Поэтому комплексное число
. Поэтому комплексное число 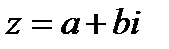 можно изображать в виде вектора
можно изображать в виде вектора 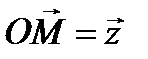 с началом в точке и концом в точке
с началом в точке и концом в точке 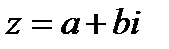 .
.
Свойства:
1.Длина вектора 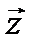 равна
равна 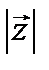 ;
;
2.Точки 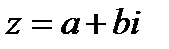 и
и 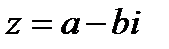 симметричны относительно действительной оси;
симметричны относительно действительной оси;
3.Точки 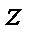 и
и 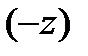 симметричны относительно точки
симметричны относительно точки 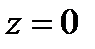 ;
;
4.Число 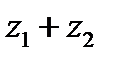 геометрически изображаются как вектор, построенный по правилу сложения векторов, соответствующих точкам
геометрически изображаются как вектор, построенный по правилу сложения векторов, соответствующих точкам 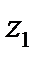 и
и 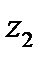 .
.
5.Расстояние между точками 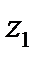 и
и 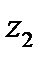 равно
равно 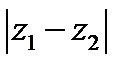 .
.
Угол между действительной осью ОХ и вектором называется аргументом комплексного числа 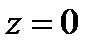 .
.
Аргумент комплексного числа 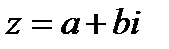 записывается так:
записывается так: 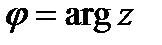 или
или 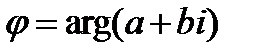 .
.
Наименьшее по абсолютной величине значение аргумента из промежутка 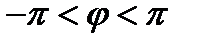 называется главным значением аргумента.
называется главным значением аргумента.
Действия вычитания и деления:
1.Разностью комплексных чисел 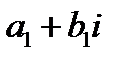 и
и 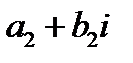 называется комплексное число
называется комплексное число 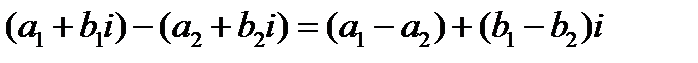 .
.
2.Делением комплексных чисел 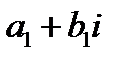 и
и 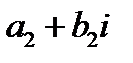 называется комплексное число:
называется комплексное число:
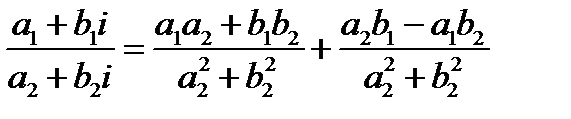 .
.
Формулы перехода от алгебраической к тригонометрической форме: 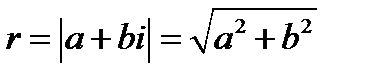
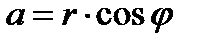 или
или 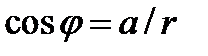
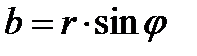 или
или 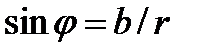
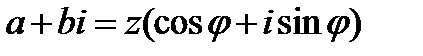
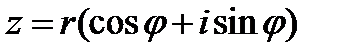 , где
, где 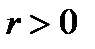 называется тригонометрической формой комплексного числа.
называется тригонометрической формой комплексного числа.
Действия над комплексными числами, заданными в тригонометрической форме:
1.Произведение комплексных чисел 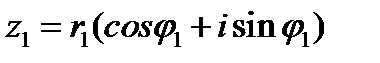 и
и 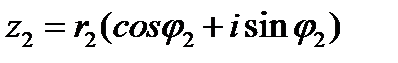 находится по формуле:
находится по формуле: 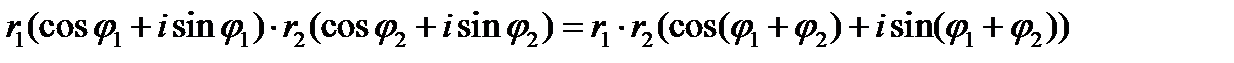
2.Частное комплексных чисел 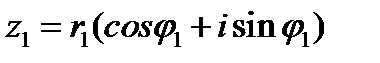 и
и 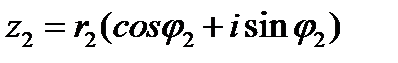 находится по формуле:
находится по формуле: 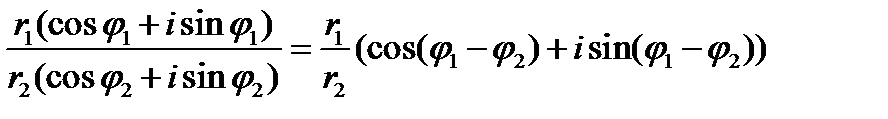 .
.
3.Для возведения 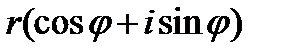 в n-ю степень используется формула:
в n-ю степень используется формула: 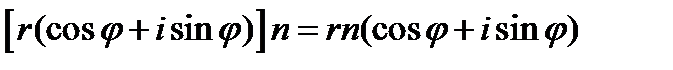 , которая называется формулой Муавра.
, которая называется формулой Муавра.
4.Для извлечения корня n-й степени из комплексного числа 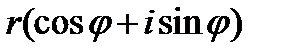 , используется формула:
, используется формула: 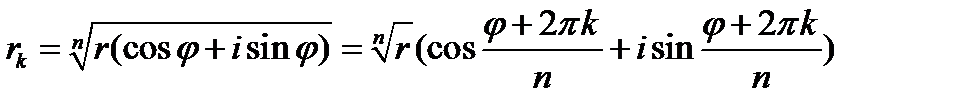 , где
, где 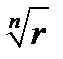 -арифметический корень.
-арифметический корень.
Найдите модуль и главное значение аргумента комплексных чисел:
1. 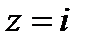 ; 2.
; 2. 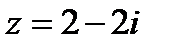 .
.
Решение:
1. 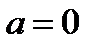 ;
; 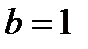 ;
; 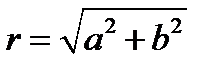 ;
; 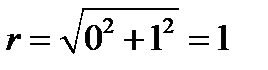 ;
; 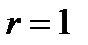 ;
; 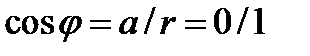 ;
; 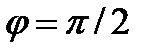
2. 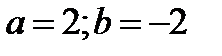 ;
; 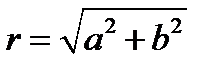
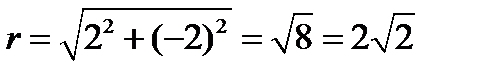 ;
; 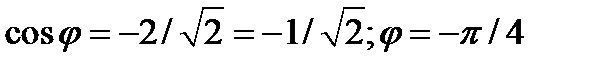
Выполните действия: 1. 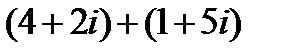 ; 2.
; 2. 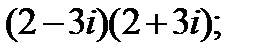 3.
3. 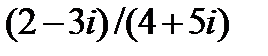
Решение:
1. 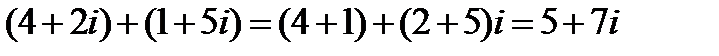 .
.
2. 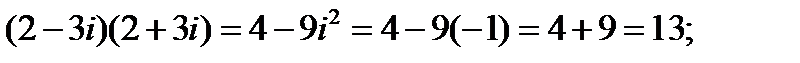
3. 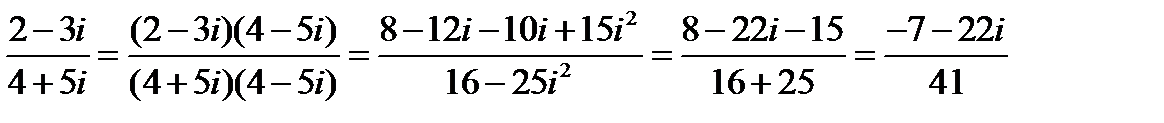
Вычислите: 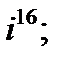
Решение: 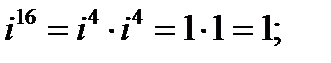
Представьте в тригонометрической форме: 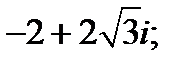
Решение:
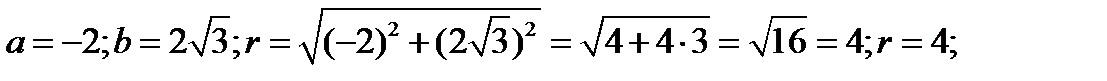
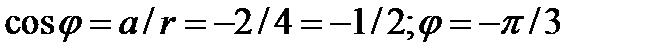 или
или 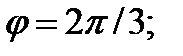
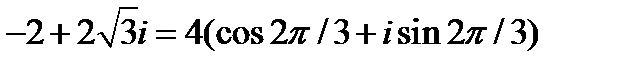 или
или
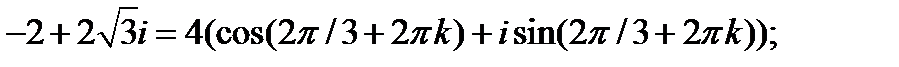
Представьте в алгебраической форме: 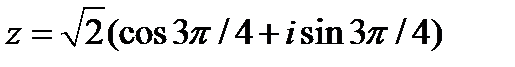
Решение:
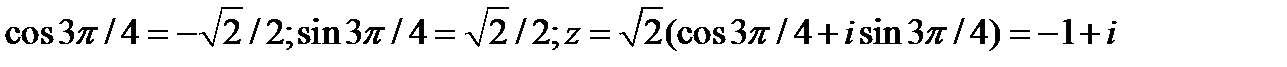
Возведите в степень: 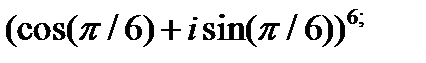 ;
;
Решение: по формуле Муавра получим:
1. 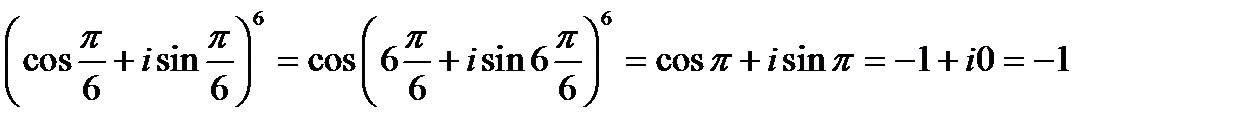
Извлеките корень из комплексного числа: 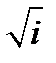
Решение: Представим число 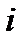 в тригонометрической форме
в тригонометрической форме
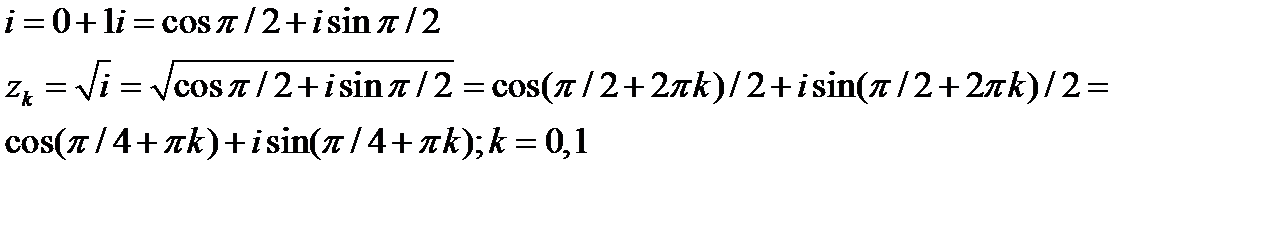
если 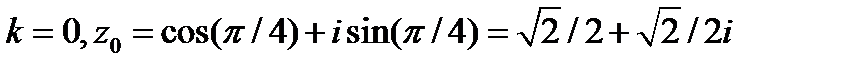
если 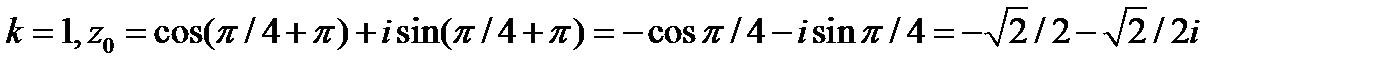
Вопросы для самопроверки:
1.Дайте определение комплексного числа.
2.Какие числа называются комплексно сопряженными?
3.Какие комплексные числа называются равными?
4.Что называется модулем комплексного числа?
5.Дайте определение тригонометрической формы комплексного числа.
6.Как осуществляется переход от записи комплексного числа., заданного в алгебраической форме, к его тригонометрической форме?
7.Как умножаются и делятся комплексные числа, заданные в тригонометрической форме?
8.Как возводится в степень комплексное число, заданное в тригонометрической форме?
9.По какой формуле извлекается корень n-й степени из комплексного числа, заданного в тригонометрической форме?



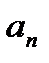 ,
, 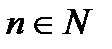 . Тогда последовательность (1)
. Тогда последовательность (1) 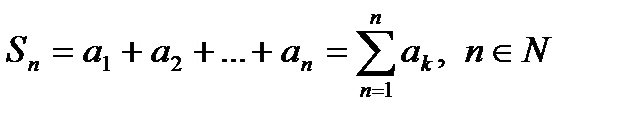 называется числовым рядом и обозначается,
называется числовым рядом и обозначается, 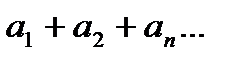 или
или 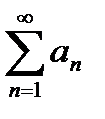 (2) числа
(2) числа 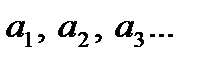 называется членами ряда (2), соответственно первым, вторым, … членами ряда.
называется членами ряда (2), соответственно первым, вторым, … членами ряда.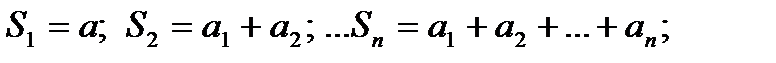 называются частичными суммами ряда (2)
называются частичными суммами ряда (2)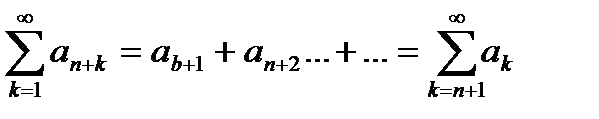 (3) называется
(3) называется 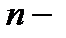 остатком ряда (2). Отметим, что у ряда (3) первым членом является
остатком ряда (2). Отметим, что у ряда (3) первым членом является 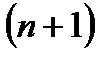 член исходного ряда (2) и к-ый член ряда (3) равен
член исходного ряда (2) и к-ый член ряда (3) равен 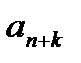 .
.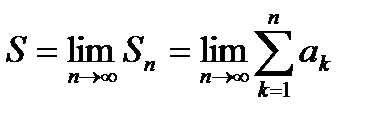 , то ряд называется сходящимся, а число, а число
, то ряд называется сходящимся, а число, а число 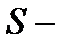 суммой сходящегося ряда.
суммой сходящегося ряда.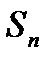 ряда (2) при неограниченном возрастании n не имеет конечного предела, то ряд называется расходящимся.
ряда (2) при неограниченном возрастании n не имеет конечного предела, то ряд называется расходящимся.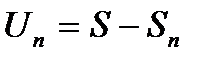 называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т. е.
называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т. е. 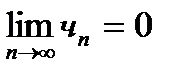 и наоборот, если остаток стремится к нулю, то ряд сходится.
и наоборот, если остаток стремится к нулю, то ряд сходится.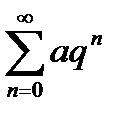
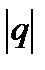 < 1 то,
< 1 то, 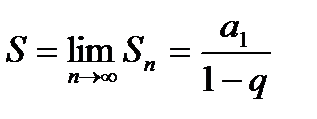 т. е. ряд сходится
т. е. ряд сходится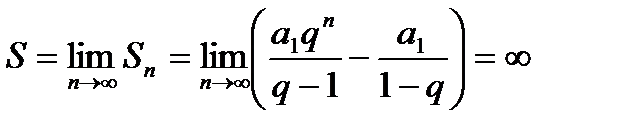 т. е. ряд расходится
т. е. ряд расходится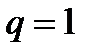 то,
то, 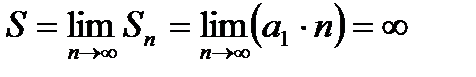 т. е. ряд расходится
т. е. ряд расходится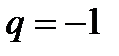 то, ряд расходится
то, ряд расходится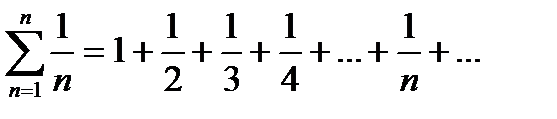 называется гармоническим
называется гармоническим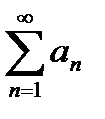 может сходиться только при условии, что его общий член
может сходиться только при условии, что его общий член 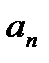 при неограниченном увеличении номера,
при неограниченном увеличении номера, 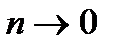 т. е.
т. е. 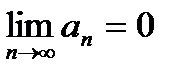 если
если 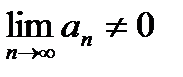 , то ряд
, то ряд 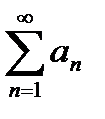 расходится это достаточный признак расходимости ряда
расходится это достаточный признак расходимости ряда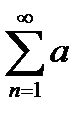 который сходится при
который сходится при 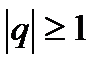 и гармонический ряд
и гармонический ряд 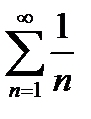 , который является расходящимся.
, который является расходящимся.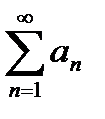 выполняется условие,
выполняется условие, 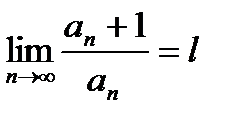 то ряд сходится при
то ряд сходится при 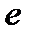 < 1 и расходится при
< 1 и расходится при 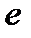 > 1. Признак Даламбера не дает ответа, если
> 1. Признак Даламбера не дает ответа, если 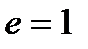 . В этом случае для исследования ряда применяется другие приемы.
. В этом случае для исследования ряда применяется другие приемы.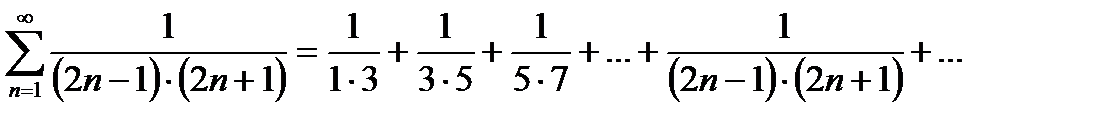
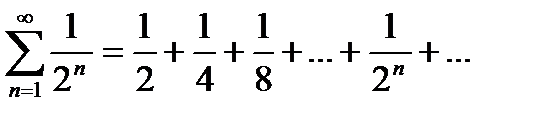
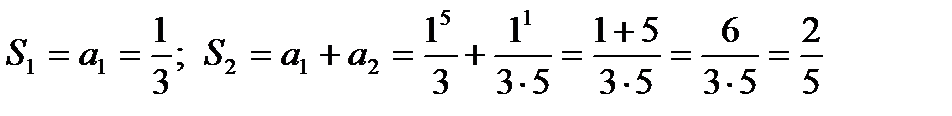
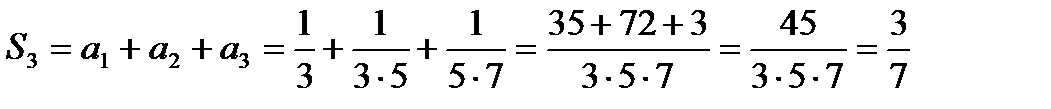
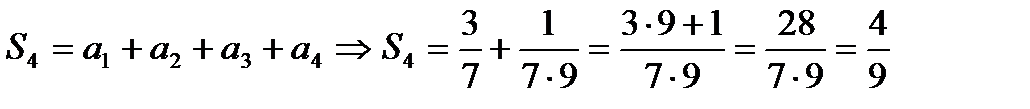
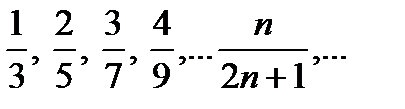
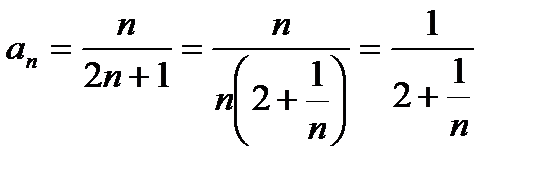
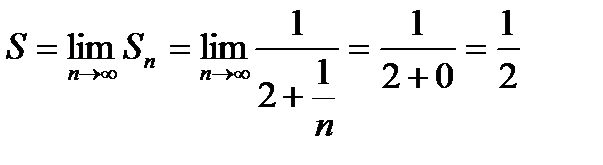
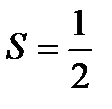 , то ряд сходится и его сумма равна
, то ряд сходится и его сумма равна 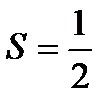
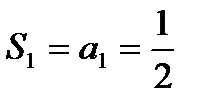
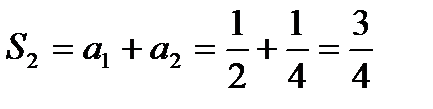
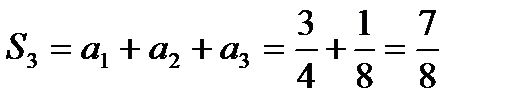
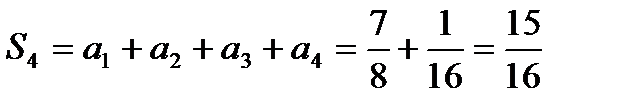 и т. д.
и т. д.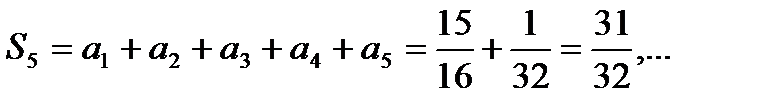
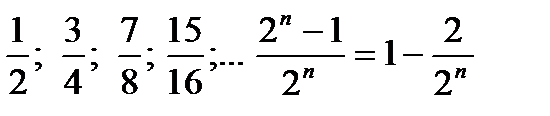
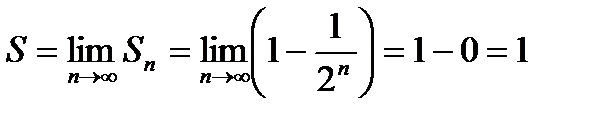
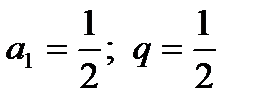 . Используя формулу
. Используя формулу 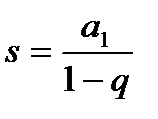 ; получим
; получим 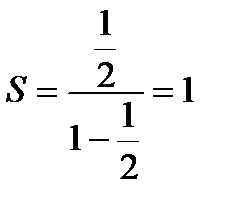 Значит ряд, сходится
Значит ряд, сходится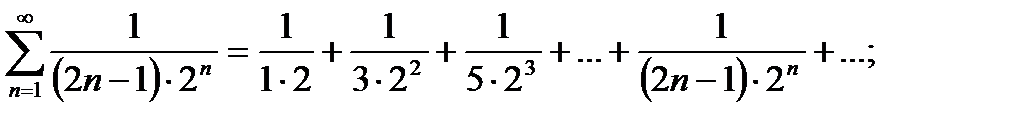
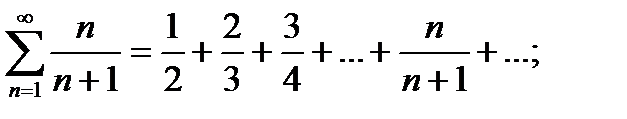
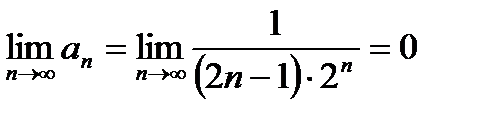
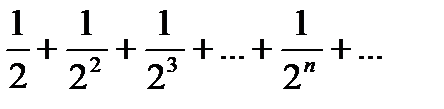 который сходится, т. к.
который сходится, т. к. 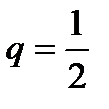 <
< 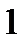
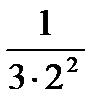 <
< 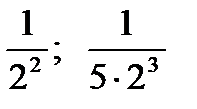 <
< 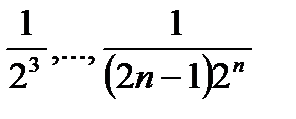 <
< 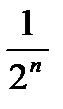 ;
;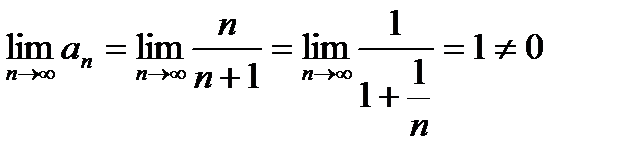
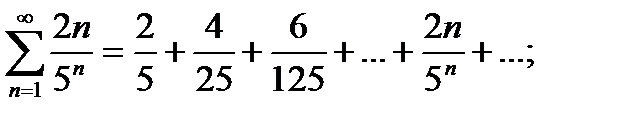
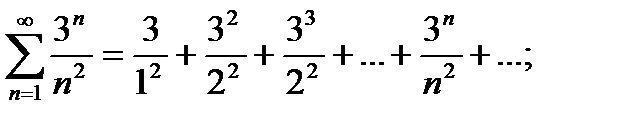
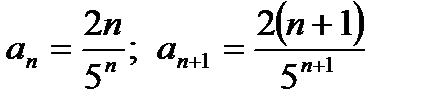
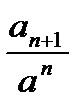 , т. е.
, т. е.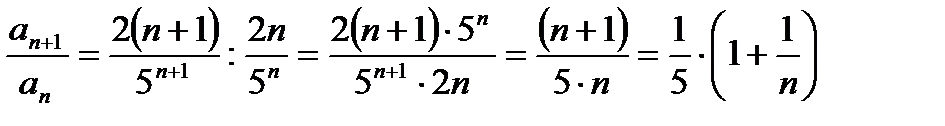
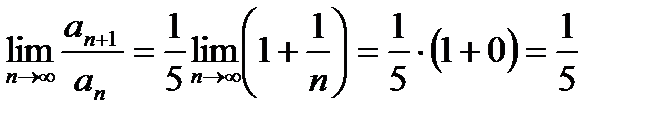 <
< 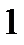
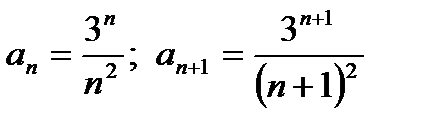
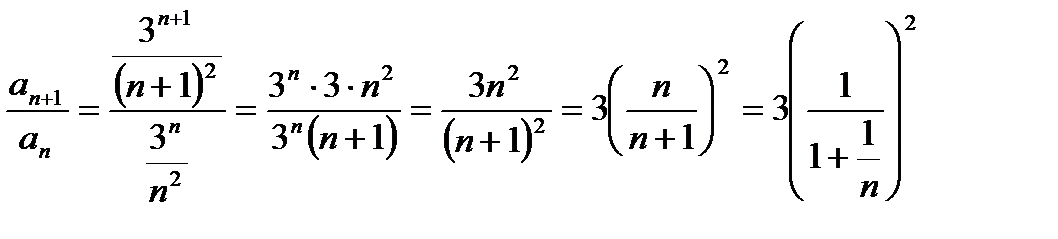
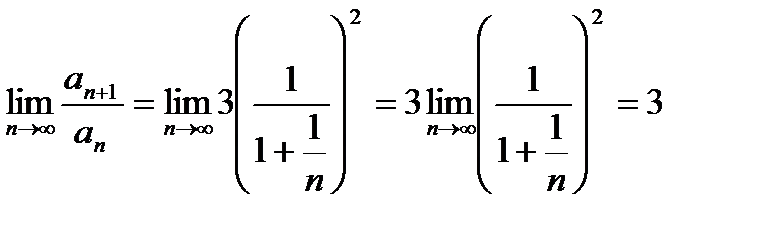 >
> 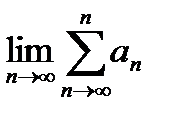 , то, как называется такой ряд?
, то, как называется такой ряд?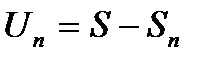
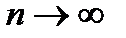 и
и 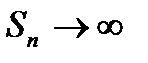 , то будет, ли гармонический ряд сходится?
, то будет, ли гармонический ряд сходится?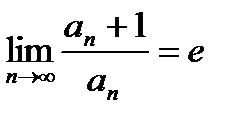 то, при каком условии ряд, сходится и при каком условии ряд расходится.
то, при каком условии ряд, сходится и при каком условии ряд расходится.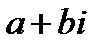 где
где 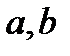 действительные числа,
действительные числа, 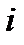 -число, определенное равенством
-число, определенное равенством 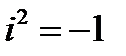 -называют мнимой единицей.
-называют мнимой единицей.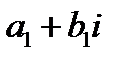 и
и 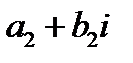 называются равными, если
называются равными, если 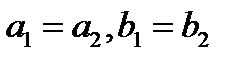
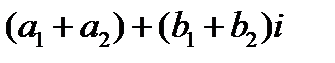
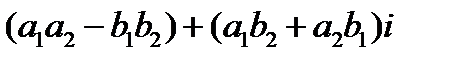
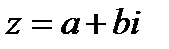 называется алгебраической формой записи комплексного числа. Действительное число
называется алгебраической формой записи комплексного числа. Действительное число 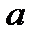 называется действительной частью комплексного числа
называется действительной частью комплексного числа 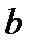 мнимой частью.
мнимой частью.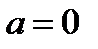 , комплексное число
, комплексное число 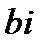 .
.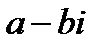 называется комплексно сопряженным с числом
называется комплексно сопряженным с числом 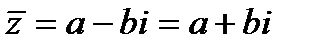
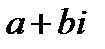 и
и 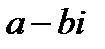 называются противоположными.
называются противоположными.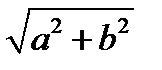 , т.е.
, т.е. 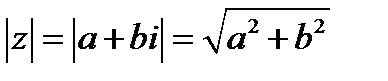 .
.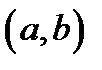
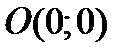 и концом в точке
и концом в точке 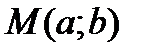 . Поэтому комплексное число
. Поэтому комплексное число 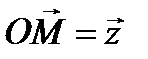 с началом в точке и концом в точке
с началом в точке и концом в точке 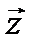 равна
равна 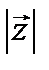 ;
;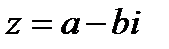 симметричны относительно действительной оси;
симметричны относительно действительной оси;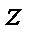 и
и 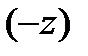 симметричны относительно точки
симметричны относительно точки 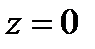 ;
;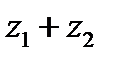 геометрически изображаются как вектор, построенный по правилу сложения векторов, соответствующих точкам
геометрически изображаются как вектор, построенный по правилу сложения векторов, соответствующих точкам 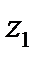 и
и 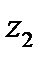 .
.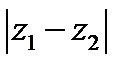 .
.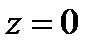 .
.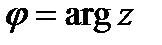 или
или 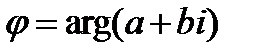 .
.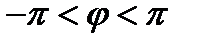 называется главным значением аргумента.
называется главным значением аргумента.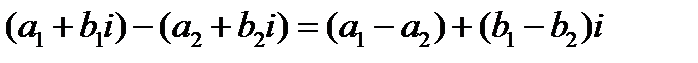 .
.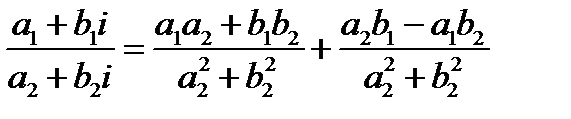 .
.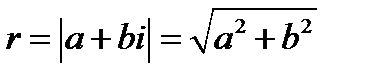
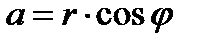 или
или 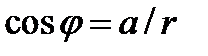
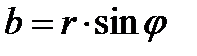 или
или 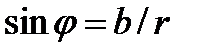
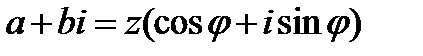
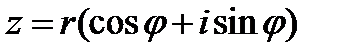 , где
, где 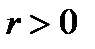 называется тригонометрической формой комплексного числа.
называется тригонометрической формой комплексного числа.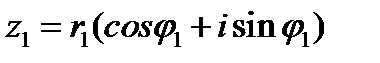 и
и 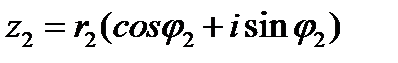 находится по формуле:
находится по формуле: 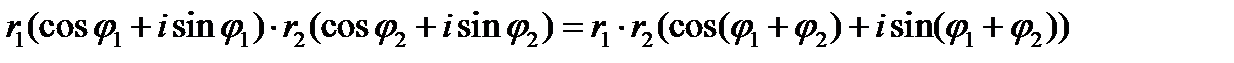
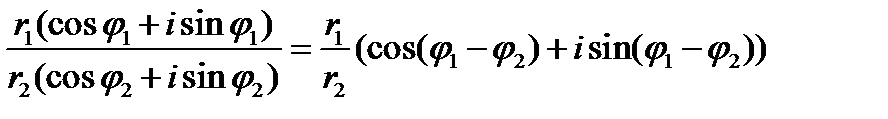 .
.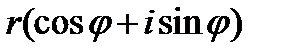 в n-ю степень используется формула:
в n-ю степень используется формула: 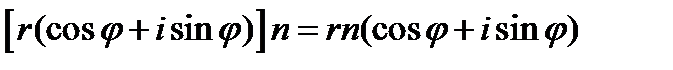 , которая называется формулой Муавра.
, которая называется формулой Муавра.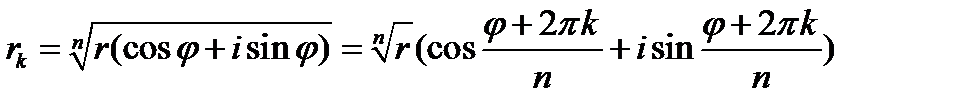 , где
, где 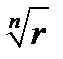 -арифметический корень.
-арифметический корень.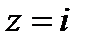 ; 2.
; 2. 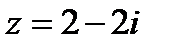 .
.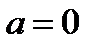 ;
; 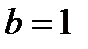 ;
; 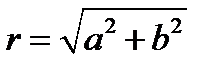 ;
; 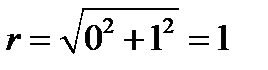 ;
; 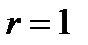 ;
; 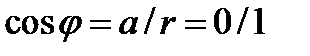 ;
; 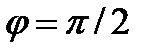
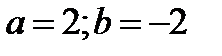 ;
; 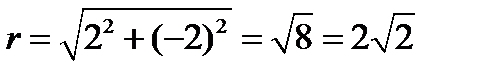 ;
; 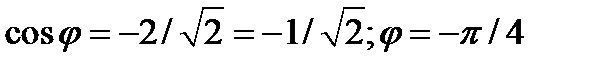
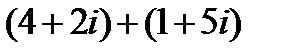 ; 2.
; 2. 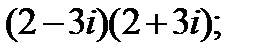 3.
3. 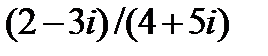
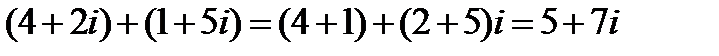 .
.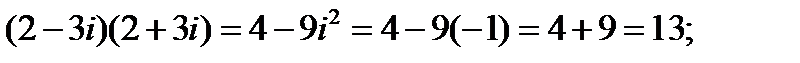
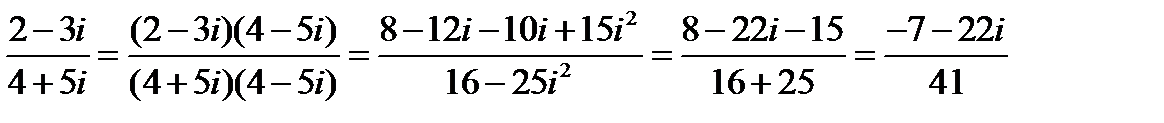
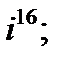
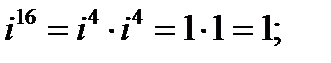
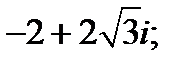
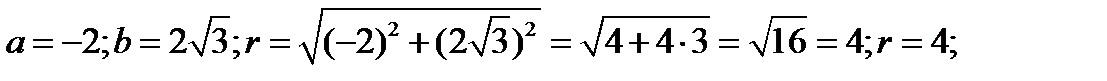
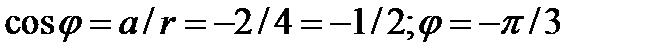 или
или 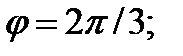
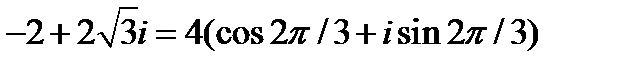 или
или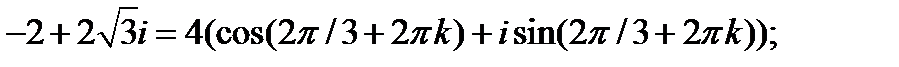
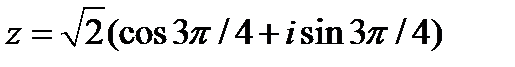
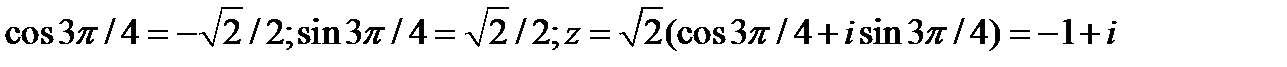
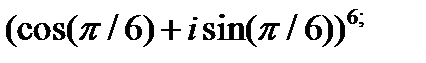 ;
;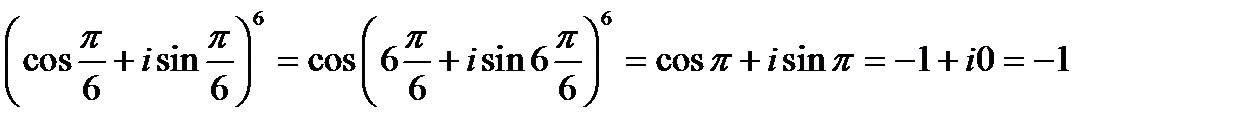
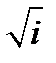
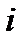 в тригонометрической форме
в тригонометрической форме