M [ X ]=2·0,3+3·0,4+4·0,3=3;
D [ X ]=(2 – 3)2·0,3+(3 – 3)2·0,4+(4 – 3)2·0,3=0,6;
 .◄
.◄
2. В урне 6 белых и 4 черных шара. Из нее три раза подряд извлекают шар, причем каждый раз вынутый шар возвращают в урну. Пусть Х – число извлеченных белых шаров. Составить закон распределения этой величины, определить ее математическое ожидание, дисперсию и среднеквадратичное отклонение.
Вероятность вынуть из урны белый шар р =0,6. Чтобы найти закон распределения случайной величины Х, воспользуемся формулой Бернулли, для которой n =3.
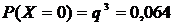 .
.
 .
.
 .
.
 .
.
Итак, закон распределения имеет вид
| Х
|
|
|
|
|
| Р
| 0,064
| 0,288
| 0,432
| 0,216
|
Определим числовые характеристики случайной величины.
M [ X ]=0,288+0,864+0,648=1,8
D [ X ]= M [ X 2] – (M [ X ])2=1·0,288+4·0,432+9·0,216 – 3,24=0,72.
 . ◄
. ◄
3. Бросают две игральные кости. Найти математическое ожидание и дисперсию случайной величины, равной сумме очков при бросании двух костей
Решение. 1 способ. Используя результат примера 1 из раздела 8, получим


2 способ. Пусть  – случайная величина, равная числу очков, выпавших на первой кости, а
– случайная величина, равная числу очков, выпавших на первой кости, а  – случайная величина, равная числу очков, выпавших на второй кости. Сумма очков, выпавшая на обеих костях, есть случайная величина, равная
– случайная величина, равная числу очков, выпавших на второй кости. Сумма очков, выпавшая на обеих костях, есть случайная величина, равная  .
.
Используя свойства математического ожидания и дисперсии ( и
и  - независимые случайные величины) и результаты задачи 1 настоящего раздела, вычислим
- независимые случайные величины) и результаты задачи 1 настоящего раздела, вычислим
 ,
,
 . ◄
. ◄
Пример. Дискретная случайная величина Х задана законом распределения:
Найти: а) математическое ожидание М(Х);
б) дисперсию D(Х) и среднее квадратическое отклонение s (Х);
в) составить функцию распределения F(х) и построить её график.
Имеем: а) по формуле 
 находим математическое ожидание Х: М(Х) = 2 × 0,2 + 4 × 0,1 + 5 × 0,3 + 7 × 0,4 = 5,1;
находим математическое ожидание Х: М(Х) = 2 × 0,2 + 4 × 0,1 + 5 × 0,3 + 7 × 0,4 = 5,1;
б) по формулам D(Х) = M (Х2) – [ M(Х)]2 и 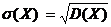 найдём дисперсию и среднее квадратическое отклонение.
найдём дисперсию и среднее квадратическое отклонение.
 = 22 × 0,2 + 42 × 0,1 + 52 × 0,3 + 72 × 0,4 = 29,5.
= 22 × 0,2 + 42 × 0,1 + 52 × 0,3 + 72 × 0,4 = 29,5.
D(Х) = 29,5 – (5,1)2 = 3,49; s(Х) =  = 1,87;
= 1,87;
в) по определению F(x) = P(X < x), т.е. F(x) есть вероятность того, что случайная X примет значение меньше, чем х.
Если х £ 2, то F(x) = P(X < 2) = 0.
Если 2 < x £ 4, то F(x) = P(X < 4) = P(X=2) = 0,2.
Если 4< x £ 5, то F(x) = P(Х < 5) = P(X=2)+(X=4) = 0,2+0,1 = 0,3.
Если 5< x £ 7, то F(x) = P(Х<7)= P(X=2)+P(X=4)+P(X=5)=0,2+0,1+0,3 = 0,6.
Если x>7, то F(x) = P(Х<7) = P(X=2) + P(X=4) + P(X=5) + P(X=7) = = 0,2+0,1+0,3+0,4 = 1.
Построим график F(x):
 ◄
◄
4. Моменты случайных величин. Пусть 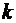 некоторое натуральное число.
некоторое натуральное число.
Моментом порядка 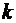 случайной величины
случайной величины  называется число
называется число
 .
.
Центральным моментом порядка 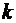 случайной величины
случайной величины  называется число
называется число
 .
.
Ковариацией (корреляционнным моментом) двух случайных величин  и
и  называется число
называется число
 .
.
Свойства ковариации.
1) Для любых двух случайных величин  и
и 

2) Для любых случайных величин  и
и 

3) Для любых случайных величин  ,
,  и
и 

 .
.
Коэффициентом корреляции двух случайных величин  и
и  называется число
называется число
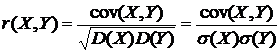 .
.
Корреляционный момент и коэффициент корреляции характеризуют степень линейной зависимости случайных величин.
Если ковариация или коэффициент корреляции двух случайных величин равны нулю, то такие величины называются некоррелированными.
Для любых двух случайных величин  и
и 

Из последней формулы следует важное свойство. Если случайные величины  и
и  некоррелированы, то
некоррелированы, то

Свойства коэффициента корреляции
1)  ,
,
где 
2)  , и
, и  , тогда и только тогда, когда существуют такие
, тогда и только тогда, когда существуют такие  и
и  , что
, что  .
.
3) Если случайные величины  и
и  независимы, то
независимы, то  .
.
Обратное утверждение неверно, т.е. из равенства нулю корреляции не следует независимость случайных величин
Пример. В ящике два шара, на каждом из которых написана цифра 1, и три шара, на каждом из которых написана цифра 2.
Один за другим вынимают два шара. Пусть  - это номер на первом шаре, а –
- это номер на первом шаре, а –  номер на втором шаре. Найти коэффициент корреляции
номер на втором шаре. Найти коэффициент корреляции  и
и  .
.
Совместный закон распределения  был найден ранее
был найден ранее
| (X,Y)
| (1,1)
| (1,2)
| (2,1)
| (2,2)
|
| P
| 1/10
| 3/10
| 3/10
| 3/10
|
Для упрощения вычислений введем случайные величины  и
и  . По первому свойству коэффициента корреляции имеем
. По первому свойству коэффициента корреляции имеем  .Совместный закон распределения величин
.Совместный закон распределения величин  может быть легко получен из закона распределения
может быть легко получен из закона распределения 
| (X 1 ,Y 1)
| (0,0)
| (0,1)
| (1,0)
| (1,1)
|
| P
| 1/10
| 3/10
| 3/10
| 3/10
|
Законы распределения  и
и  могут быть также легко получены по свойствам вероятностей
могут быть также легко получены по свойствам вероятностей  :
:
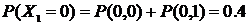 ,
,  .
.
 ,
,  .
.
Тогда 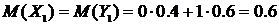 ,
,  ,
,  .
.
Окончательно имеем
 ,
,
 . ◄
. ◄
5. Биномиальный закон распределения дискретной случайной величины. Закон распределения дискретной случайной величины Х, которая может принимать n +1 значение 0,1,2,…, n, описываемый формулой Бернулли  , называется биномиальным. Запишем биномиальный закон в виде таблицы
, называется биномиальным. Запишем биномиальный закон в виде таблицы
Определим числовые характеристики биномиального распределения. Пусть Х – число появлений события А в n испытаниях. Если обозначим через Xk – число появлений события А в k -ом испытании, то  .
.
Закон распределения случайной величины Xk имеет вид
Легко видеть, что M [ Xk ]= p, D [ Xk ]= pq. Тогда для случайной величины Х
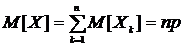 .
.  .
.  .
.
Пример. Предприятие выпускает 90% изделий высшего сорта. Составить закон распределения случайной величины Х – числа изделий высшего сорта из трёх взятых наудачу изделий. Найти M(X), D(X), s(Х).
Решение: Случайная величина Х – число изделий высшего сорта среди трёх отобранных изделий может принимать одно из значений: 0, 1, 2, 3. Вероятности этих значений вычисляются по формуле Бернулли:
 . Известно, что n = 3; p = 0,9; q = 0,1; k= 0,1,2,3, тогда
. Известно, что n = 3; p = 0,9; q = 0,1; k= 0,1,2,3, тогда
P1(X=0) = (0,1)3 = 0,001.
P2(X=1) = C31 ∙ 0,91 ∙ 0,12 = 0,027.
P3(X=2) = C32 ∙ 0,92 ∙ 0,1 = 0,243.
P4(X=3) = 0,93 = 0,729.
Проверка:
Р= Р3(Х=0)+Р3(Х=1)+Р3(Х=2)+Р3(Х=3)= 0,001+0,027+0,243 +0,729 = 1.
Закон распределения случайной величины Х:
| X
|
|
|
|
|
| P
| 0,001
| 0,027
| 0,243
| 0,729
|
M(X), D(X), s (X) случайной величины, распределённой по биноминальному закону, находятся по формулам:
M(X) = np, D(X) = npq, s (X) =  .
.
M(X) = 3 ∙ 0,9 = 2,7; D(X) = 3 ∙ 0,9 ∙ 0,1 = 0,27; s (X) =  = 0,53.
= 0,53.
◄
6. Закон распределения Пуассона дискретной случайной величины. Этот закон определяется формулой Пуассона
 , где λ = np.
, где λ = np.
Случайная величина Х – число появлений события А в n испытаниях при большом n и малой вероятности р имеет распределение Пуассона



 .◄
.◄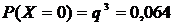 .
. .
. .
. .
. . ◄
. ◄

 – случайная величина, равная числу очков, выпавших на первой кости, а
– случайная величина, равная числу очков, выпавших на первой кости, а  – случайная величина, равная числу очков, выпавших на второй кости. Сумма очков, выпавшая на обеих костях, есть случайная величина, равная
– случайная величина, равная числу очков, выпавших на второй кости. Сумма очков, выпавшая на обеих костях, есть случайная величина, равная  .
. ,
, . ◄
. ◄
 находим математическое ожидание Х: М(Х) = 2 × 0,2 + 4 × 0,1 + 5 × 0,3 + 7 × 0,4 = 5,1;
находим математическое ожидание Х: М(Х) = 2 × 0,2 + 4 × 0,1 + 5 × 0,3 + 7 × 0,4 = 5,1;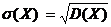 найдём дисперсию и среднее квадратическое отклонение.
найдём дисперсию и среднее квадратическое отклонение. = 22 × 0,2 + 42 × 0,1 + 52 × 0,3 + 72 × 0,4 = 29,5.
= 22 × 0,2 + 42 × 0,1 + 52 × 0,3 + 72 × 0,4 = 29,5. = 1,87;
= 1,87; ◄
◄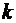 некоторое натуральное число.
некоторое натуральное число. называется число
называется число .
. .
. .
.

 и
и 

 .
.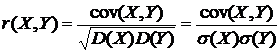 .
.

 ,
,
 , и
, и  , тогда и только тогда, когда существуют такие
, тогда и только тогда, когда существуют такие  и
и  , что
, что  .
. .
. был найден ранее
был найден ранее и
и  . По первому свойству коэффициента корреляции имеем
. По первому свойству коэффициента корреляции имеем  .Совместный закон распределения величин
.Совместный закон распределения величин  может быть легко получен из закона распределения
может быть легко получен из закона распределения 
 и
и  могут быть также легко получены по свойствам вероятностей
могут быть также легко получены по свойствам вероятностей  :
: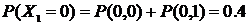 ,
,  .
. ,
,  .
.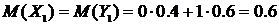 ,
,  ,
,  .
. ,
, . ◄
. ◄ , называется биномиальным. Запишем биномиальный закон в виде таблицы
, называется биномиальным. Запишем биномиальный закон в виде таблицы


 .
.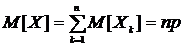 .
.  .
.  .
. . Известно, что n = 3; p = 0,9; q = 0,1; k= 0,1,2,3, тогда
. Известно, что n = 3; p = 0,9; q = 0,1; k= 0,1,2,3, тогда .
. = 0,53.
= 0,53. , где λ = np.
, где λ = np.





