 . ◄
. ◄
4. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, ч то извлеченный шар окажется белым, если равно возможны все предположения о первоначальном составе шаров.
Обозначим события: А – извлечен белый шар;
В 1 – первоначально белых шаров в урне не было;
В 2 – первоначально в урне был один белый шар;
В 3 – первоначально в урне было два белых шара.
Заметим, что  ,
,  ,
,  ,
,  . Тогда по формуле полной вероятности
. Тогда по формуле полной вероятности
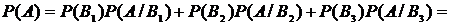
 . ◄
. ◄
5. В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с прицелом, равна 0,95, для винтовки без прицела соответствующая вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок делает один выстрел из произвольной винтовки.
Пусть А – мишень поражена; В 1 – произведен выстрел из винтовки с прицелом; В 1 – выстрел из винтовки без прицела. Тогда  ,
,  и по формуле полной вероятности
и по формуле полной вероятности
 . ◄
. ◄
6. По цели произведено три последовательных выстрела. Вероятность попадания при первом выстреле р 1=0,3, при втором р 2=0,6, при третьем р 3=0,8. При одном попадании вероятность поражения цели r 1=0,4, при двух попаданиях r 2=0,7, при трех попаданиях r 3=1. Определить вероятность поражения цели при трех выстрелах.
Рассмотрим полную группу несовместных событий:
В 1 – было одно попадание;
В 2 – было два попадания;
В 3 – было три попадания;
В 4 – не было ни одного попадания.
Определим вероятность каждого события. По теоремам умножения и сложения вероятностей будем иметь
 .
.
 .
.
 .
.
 .
.
Пусть событие А – цель поражена. Выпишем условные вероятности поражения цели при осуществлении каждого из событий В 1, В 2, В 3, и В 4.
 ,
,  ,
,  ,
,  .
.
Тогда по формуле полной вероятности
 .◄
.◄
2. Если известно, что в результате опыта событие  произошло, то эта информация может изменить вероятности гипотез: повышаются вероятности тех гипотез, при которых событие
произошло, то эта информация может изменить вероятности гипотез: повышаются вероятности тех гипотез, при которых событие  происходит с большей вероятностью, и уменьшаются вероятности остальных. Для переоценки вероятностей гипотез при известном результате опыта используется так называемая теорема гипотез, или формула Байеса:
происходит с большей вероятностью, и уменьшаются вероятности остальных. Для переоценки вероятностей гипотез при известном результате опыта используется так называемая теорема гипотез, или формула Байеса:
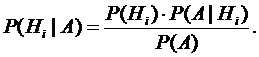
(В знаменателе дроби в правой части равенства стоит полная вероятность события  ).
).
Примеры.
1. В студенческой группе 20 студентов. Из них 5 отличников, которые знают все экзаменационные вопросы, 8 студентов знают ответы на 70 % вопросов и 7 — на 50 %. Первый вызванный студент ответил на первый вопрос экзаменационного билета. Найти вероятность того, что он отличник.
Будем считать гипотезой  то, что данный студент является отличником,
то, что данный студент является отличником,  — что он принадлежит ко второй группе,
— что он принадлежит ко второй группе,  — к третьей. Тогда вероятности гипотез равны:
— к третьей. Тогда вероятности гипотез равны:

Найдем условную вероятность события  — правильного ответа на первый вопрос — при осуществлении каждой гипотезы:
— правильного ответа на первый вопрос — при осуществлении каждой гипотезы:



Следовательно, полная вероятность события  равна
равна

Применяя формулу Байеса, находим:
 ◄
◄
2. 30% приборов собирает специалист высокой квалификации и 70% специалист средней квалификации. Надежность работы прибора, собранного специалистом высокой квалификации, 0,9, надежность прибора, собранного специалистом средней квалификации, 0,8. Взятый прибор оказался надежным. Определить вероятность того, что он собран специалистом высокой квалификации.
Событие А – безотказная работа прибора;
В 1 – прибор собран специалистом высокой квалификации;
В 2 – прибор собран специалистом средней квалификации.
Выпишем вероятности гипотез:  ,
,  .
.
Условные вероятности события А:  ,
,  .
.
Вероятность события А:  . Определим вероятность гипотезы В 1 при условии, что событие А произошло
. Определим вероятность гипотезы В 1 при условии, что событие А произошло
 .◄
.◄
3. Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие попало, если вероятности попадания в цель каждым из орудий равны р 1=0,4, р 2=0,3, р 3=0,5.
Обозначим события: А – два орудия попали в цель;
В 1 – первое орудие попало в цель;
В 2 – первое орудие не попало в цель.
Вероятности гипотез:  ,
,  .
.
Условные вероятности события А:
 .
.
 .
.
По формуле Байеса

 . ◄
. ◄
Вопросы для самопроверки
1. Что понимается под суммой двух событий?
2. Сформулируйте теорему сложения вероятностей для несовместных событий?
3. Что понимается под полной группой событий? Чему равна сумма вероятностей несовместных событий, составляющих полную группу?
4. Какие события называются противоположными? Чему равна сумма вероятностей противоположных событий?
5. Дайте определение условной вероятности. Какие события называются независимыми?
6. Что понимается под произведением двух событий?
7. Сформулируйте теорему умножения вероятностей для независимых и зависимых событий.
8. Докажите формулу полной вероятности.
9. Докажите формулу Байеса.
Повторные независимые
Испытания
В теме изучаются методы решения задачи, в которой один и тот же опыт повторяется несколько раз. В результате каждого опыта может появиться или не появиться интересующее нас событие. Однако нас интересует не результат отдельного опыта, а результат серии опытов, т. е. какова вероятность появления того или иного числа событий в серии опытов. Характерным примером такой задачи являются различного рода выборки. Когда образована выборка и производится ее изучение, то каждый элемент ее обследуется и устанавливается наличие или отсутствие того или иного фактора. Обследование одного элемента выборки и есть опыт или испытание. Обследование всех элементов выборки, проводимое в одинаковых условиях, есть повторение испытаний, рассматриваемое в задаче о повторении опытов.
Формула Пуассона наряду с задачей повторения испытаний используется также для расчета вероятности появления различного числа событий (например, точек или других элементов) в какой-либо области (площади, объеме или во времени). При этом должны соблюдаться следующие условия: события (точки) в области распределены в общем равномерно;положение каждого события (точки) случайное, независимое друг от друга;события (точки) появляются в области поодиночке, а не парами, тройками и т. д.
При решении задач с использованием формулы Пуассона исходные данные могут встречаться в двух вариантах:
1) в условии задачи указывается вероятность р появления события в одном испытании и число испытаний n;
2) в условии задачи указывается среднее число  появлений события за какую-либо единицу области (площади, объема, времени) и размер области s {площади, объема, времени), внутри которой появляются интересующие события.
появлений события за какую-либо единицу области (площади, объема, времени) и размер области s {площади, объема, времени), внутри которой появляются интересующие события.
В первом случае параметр распределения Пуассона определяется как произведение вероятности р и числа п испытаний:  = пр.
= пр.
Во втором случае этот параметр определяется произведением среднего числа появлений события и размера области: 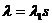 .
.
Дальнейший расчет вероятности по формуле Пуассона одинаков в обоих случаях.
1. Формула Бернулли. Рассмотрим случай, когда требуется определить не вероятность осуществления некоторого события  в одном испытании, а вероятность того, что это событие произойдет заданное количество раз в серии из
в одном испытании, а вероятность того, что это событие произойдет заданное количество раз в серии из  опытов. Будем считать при этом, что вероятность
опытов. Будем считать при этом, что вероятность  в каждом опыте одинакова и результат каждого опыта не зависит от результатов остальных. Такая постановка задачи называется схемой независимых испытаний. При выполнении указанных условий вероятность того, что при проведении
в каждом опыте одинакова и результат каждого опыта не зависит от результатов остальных. Такая постановка задачи называется схемой независимых испытаний. При выполнении указанных условий вероятность того, что при проведении  независимых испытаний событие
независимых испытаний событие  будет наблюдаться ровно
будет наблюдаться ровно  раз (неважно, в каких именно опытах), определяется по формуле Бернулли:
раз (неважно, в каких именно опытах), определяется по формуле Бернулли:

где  — вероятность появления
— вероятность появления  в каждом испытании, а
в каждом испытании, а  — вероятность того, что в данном опыте событие
— вероятность того, что в данном опыте событие  не произошло.
не произошло.
В частности, отсюда Рn (0)= qn, Рn (1)= npqn- 1, …, Рn (n)= pn.
Примеры.
1. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Событие А – достали белый шар. Тогда вероятности  ,
,  . По формуле Бернулли требуемая вероятность
. По формуле Бернулли требуемая вероятность
 . ◄
. ◄
2. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Вероятность рождения девочки  , тогда
, тогда  .
.
Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:
 ,
,  ,
,
 ,
,  .
.
Следовательно, искомая вероятность
 . ◄
. ◄
3. Правильная игральная кость бросается четыре раза. Найти вероятность того, что шесть очков выпадут ровно два раза.
Обозначим  {выпадение на одной кости шести очков}. Очевидно, что в этом случае испытания независимы, и мы имеем схему Бернулли с
{выпадение на одной кости шести очков}. Очевидно, что в этом случае испытания независимы, и мы имеем схему Бернулли с  ,
,  , а так как кость правильная
, а так как кость правильная  . Вычислим
. Вычислим
 .
.
Подставляя эти значения в формулу Бернулли, получим искомую вероятность
 . ◄
. ◄
4. Вероятность появления события  в каждом из 5 независимых испытаний равна 0.8. Найти вероятность того, что событие А произойдет
в каждом из 5 независимых испытаний равна 0.8. Найти вероятность того, что событие А произойдет
а) не менее трех раз б) не более двух раз.
Имеем 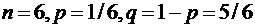 ,
,
Подставляя эти значения в формулу для  , получим
, получим
а) 




 .
.
б) 


Нетрудно видеть, что событие а) = { не менее двух попаданий при шести выстрелах, т.е. 2, 3, 4, 5, 6 попаданий} и событие б) ={не более одного попадания при шести выстрелах, т.е. 0 и 1 попадание } составляют полную группу событий с суммой вероятностей равной 1,  . Поэтому вероятность события б) можно подсчитать, используя значение
. Поэтому вероятность события б) можно подсчитать, используя значение  , полученное в а)
, полученное в а)  . ◄
. ◄
■▬▬▬►
2. Число наступлений события  называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления
называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления  любое другое количество раз.
любое другое количество раз.
Наивероятнейшее число наступлений события  в
в  испытаниях заключено между числами
испытаниях заключено между числами  и
и  .
.
Замечание. Если  – целое число, то наивероятнейших чисел два:
– целое число, то наивероятнейших чисел два:  и
и  .
.
Пример. Вероятность попадания в цель при каждом выстреле из лука равна 1/3. Производится шесть выстрелов. Какова вероятность ровно двух попаданий? Какова вероятность не менее двух попаданий? Каково наивероятнейшее число попаданий?
Обозначим A = {попадание при одном выстреле} p = 1/3, q = 1 – 1/3 = 2/3. Число выстрелов n = 6. Естественно предположить, что выстрелы не зависят друг от друга, и мы имеем схему Бернулли.
Ответ на первый вопрос находим по формуле Бернулли, n = 4, m =2
 .
.
Ответ на второй вопрос можно найти по формуле для  . Однако проще найти по этой формуле, вероятность не более одного попадания и вычесть эту вероятность из 1.
. Однако проще найти по этой формуле, вероятность не более одного попадания и вычесть эту вероятность из 1.

 .
.
В этом рассуждении мы использовали тот факт, что событие B 1 = { не менее двух попаданий при шести выстрелах, т.е. 2, 3, 4, 5, 6 попаданий} и событие B 2= { не более одного попадания при шести выстрелах, т.е. 0 и 1 попадание } составляют полную группу событий с суммой вероятностей равной 1. Для ответа на третий вопрос найдем
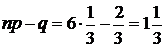 ,
,  ,
,
следовательно, наивероятнейшее число попаданий, лежащее между этими числами, равно двум. ◄
◄▬▬▬■
3. Формула Пуассона. При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например, 0,951000 вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз используют формулу Пуассона
 ,
,
где λ = np =const – среднее число появлений события в n испытаниях.
Примеры.
1. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
N =1000, p =0,002, λ = np =2, k =3.
Искомая вероятность
 . ◄
. ◄
2. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.
n =500, p =0,004, λ =2.
По теореме сложения вероятностей
 . ◄
. ◄
3. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.
λ = np =1000·0,003=3
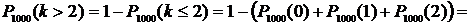
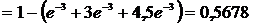 .
.
 ◄
◄
4. Радиоаппаратура состоит из 2000 элементов. Вероятность отказа одного элемента в течение года равна 0,001. Какова вероятность отказа двух элементов за год? Какова вероятность отказа не менее двух элементов за год?
Работу каждого элемента рассматриваем как отдельное испытание. Обозначим А = { отказ элемента за год }. Имеем n = 2000, p = p (А)= 0.001, λ = n p = 2000∙0,001 = 2. По формуле Пуассона
 .
.
Ответ на второй вопрос дается формулой

 . ◄
. ◄
Теоремы Муавра-Лапласа.
1. Рассмотрим случай, когда число успехов 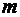 растет с ростом
растет с ростом  , а вероятность успеха
, а вероятность успеха  постоянна.
постоянна.
Теорема Муавра-Лапласа (локальная). Положим 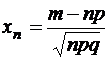 . Предположим, что m →∞, n →∞ и величины xn являются ограниченными. Тогда
. Предположим, что m →∞, n →∞ и величины xn являются ограниченными. Тогда
 .
.
В частности, если xn → x, то

Рассмотрим приближенную формулу для вероятности того, что событие наступило не менее m 1 и не более m 2 раз в n испытаниях, когда n велико. Предположим, что числа m 1 и m 2 растут с ростом n, а вероятность успеха p постоянна.
2. Теорема Муавра-Лапласа (интегральная). Положим  . Предположим, что m 1→∞, n →∞ и величины an и bn являются ограниченными. Тогда
. Предположим, что m 1→∞, n →∞ и величины an и bn являются ограниченными. Тогда
 .
.
Введем функцию Гаусса φ(x) и функцию ЛапласаΦ (x)
 ,
,  .
.
Тогда локальную теорему можно записать в виде
 ,
,
где  ,
,
а интегральную теорему в виде
 ,
,
где  .
.
Замечание. Приближенными формулами Лапласа на практике пользуются в случае, если npq >10. Если npq <10, то эти формулы приводят к большим погрешностям.
Примеры.
1. Вероятность появления события  в каждом из 900 независимых испытаний равна 0.8. Найти вероятность того, что событие
в каждом из 900 независимых испытаний равна 0.8. Найти вероятность того, что событие  произойдет
произойдет
а) 750 раз, б) не менее 710 раз и не более 740 раз.
Из условия следует, что n = 900, p = 0.8, величина q = 0.2 и npq = 144 >10 и можно использовать приближенные формулы.
а) m = 750, найдем 
 .
.
По таблице значений функции Гаусса находим φ (2.5) = 0.0175. Искомая вероятность равна
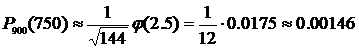 .
.
б) m 1 = 710, m 2 = 740, найдем an и bn

 .
.
По таблице значений функции Лапласа 
 ,
,
Искомая вероятность равна
 .◄
.◄
2. Сколько раз с вероятностью 0.0484 можно ожидать появления события 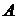 в 100 независимых испытаниях, если вероятность его появления в отдельном испытании
в 100 независимых испытаниях, если вероятность его появления в отдельном испытании  ?
?
Из условия следует, что n = 100, Pn(m) = 0.0484, p = 0.5, величина q = 0.5, требуется определить m. (Т.к. npq = 25 >10 можно использовать приближенные формулы).
Найдем x
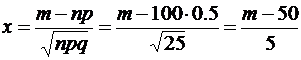 .
.
Имеем
 .
.
Отсюда находим  . По таблице значений функции Гаусса находим x = 1.09. Подставляя это значение в выражение для x, получим
. По таблице значений функции Гаусса находим x = 1.09. Подставляя это значение в выражение для x, получим
 .
.
Поскольку 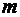 – целое число, то
– целое число, то  . ◄
. ◄
3. Найти вероятность того, что при 150 выстрелах мишень будет поражена ровно 70 раз, если вероятность попадания при одном выстреле равна 0.4.
Данная задача решается с использованием схемы Бернулли, А = {попадание при одном выстреле }, n = 100, p = p (А)= 0.4, q = 1 – p = 0.6, m =70. (Т.к. npq = 36 >10 можно использовать приближенные формулы).
 .
.
Тогда
 . ◄
. ◄
5. Город ежедневно посещают 1000 туристов, которые днем идут обедать. Каждый из них выбирает для обеда один из двух городских ресторанов с равными вероятностями и независимо друг от друга. Владелец одного из ресторанов желает, чтобы с вероятностью приблизительно 0.99 все пришедшие в его ресторан туристы могли там одновременно пообедать. Сколько мест должно быть в его ресторане?
Пусть А = {турист пообедал в данном ресторане}. Вероятность наступления события А: p = p (А) =0.5, n = 1000. Владелец ресторана желает, чтобы вероятность переполнения ресторана была равна 1-0.99=0.01. Число мест в ресторане 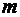 должно быть таким, чтобы вероятность того, что ресторан посетит более, чем
должно быть таким, чтобы вероятность того, что ресторан посетит более, чем 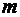 (и не более 1000) туристов была равна 0.01. Т.е. должно выполняться равенство
(и не более 1000) туристов была равна 0.01. Т.е. должно выполняться равенство
 . Имеем
. Имеем

 .
.
Тогда

 , или
, или  .
.
Используя таблицы для функции Лапласа, находим
 , значит
, значит  . Следовательно, в ресторане должно быть 537 мест. ◄
. Следовательно, в ресторане должно быть 537 мест. ◄
Вопросы для самопроверки
1. Дайте определение последовательности независимых испытаний, изложите схему Бернулли.
2. Сформулируйте условия задач, для решения которых применяется формула Бернулли.
3. Как определяется число сочетаний из и элементов по т?
3. При каких условиях из формулы Бернулли получается формула Пуассона?
4. Изложите два случая определения параметра формулы Пуассона.
5. Что такое наивероятнейшее число появлений события? Как оно определяется?
6. Какова асимптотическая формула биномиального распределения?
II. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
Понятие случайной величины — основное в теории вероятностей. Применение теории вероятностей для решения практических задач в первую очередь связано с этим понятием. Следует хорошо разобрать методику задания случайной величины дискретного типа с помощью таблицы или многоугольника распределения, а непрерывного типа — с помощью дифференциальной функции или кривой распределения, использование этих понятий для расчета вероятности попадания случайной величины в заданный интервал. Далее необходимо усвоить понятия математического ожидания и дисперсии как числовых характеристик наиболее важных свойств случайной величины.
Во многих задачах теории вероятности удобнее оперировать не понятием случайного события, для которого существуют только две возможности: оно может произойти или не произойти в результате опыта, а понятием так называемой случайной величины, то есть величины, которая при проведенном испытании может принимать различные значения, причем заранее не известно, какие именно. Если возможный диапазон значений такой величины представляет собой конечное или счетное множество, она называется дискретной случайной величиной, а если эти значения заполняют целиком некоторый интервал — непрерывной случайной величиной.



 . ◄
. ◄ ,
,  ,
,  ,
,  . Тогда по формуле полной вероятности
. Тогда по формуле полной вероятности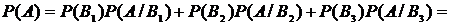
 . ◄
. ◄ ,
,  и по формуле полной вероятности
и по формуле полной вероятности . ◄
. ◄ .
. .
. .
. .
. ,
,  ,
,  .
. .◄
.◄ произошло, то эта информация может изменить вероятности гипотез: повышаются вероятности тех гипотез, при которых событие
произошло, то эта информация может изменить вероятности гипотез: повышаются вероятности тех гипотез, при которых событие 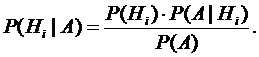
 то, что данный студент является отличником,
то, что данный студент является отличником,  — что он принадлежит ко второй группе,
— что он принадлежит ко второй группе,  — к третьей. Тогда вероятности гипотез равны:
— к третьей. Тогда вероятности гипотез равны:




 ◄
◄ ,
,  .
. ,
,  .
. . Определим вероятность гипотезы В 1 при условии, что событие А произошло
. Определим вероятность гипотезы В 1 при условии, что событие А произошло .◄
.◄ ,
,  .
. .
. .
.
 . ◄
. ◄ появлений события за какую-либо единицу области (площади, объема, времени) и размер области s {площади, объема, времени), внутри которой появляются интересующие события.
появлений события за какую-либо единицу области (площади, объема, времени) и размер области s {площади, объема, времени), внутри которой появляются интересующие события. = пр.
= пр.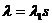 .
. опытов. Будем считать при этом, что вероятность
опытов. Будем считать при этом, что вероятность  раз (неважно, в каких именно опытах), определяется по формуле Бернулли:
раз (неважно, в каких именно опытах), определяется по формуле Бернулли:
 — вероятность появления
— вероятность появления  — вероятность того, что в данном опыте событие
— вероятность того, что в данном опыте событие  ,
,  . По формуле Бернулли требуемая вероятность
. По формуле Бернулли требуемая вероятность . ◄
. ◄ , тогда
, тогда  .
. ,
,  ,
, ,
,  .
. . ◄
. ◄ {выпадение на одной кости шести очков}. Очевидно, что в этом случае испытания независимы, и мы имеем схему Бернулли с
{выпадение на одной кости шести очков}. Очевидно, что в этом случае испытания независимы, и мы имеем схему Бернулли с  ,
,  , а так как кость правильная
, а так как кость правильная  . Вычислим
. Вычислим .
. . ◄
. ◄ в каждом из 5 независимых испытаний равна 0.8. Найти вероятность того, что событие А произойдет
в каждом из 5 независимых испытаний равна 0.8. Найти вероятность того, что событие А произойдет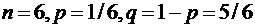 ,
, , получим
, получим




 .
.


 . Поэтому вероятность события б) можно подсчитать, используя значение
. Поэтому вероятность события б) можно подсчитать, используя значение  , полученное в а)
, полученное в а)  . ◄
. ◄ испытаниях заключено между числами
испытаниях заключено между числами  и
и  .
. .
.
 .
.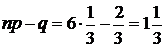 ,
,  ,
, ,
, . ◄
. ◄ . ◄
. ◄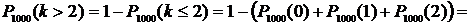
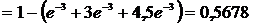 .
. ◄
◄ .
.
 . ◄
. ◄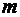 растет с ростом
растет с ростом  постоянна.
постоянна.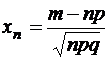 . Предположим, что m →∞, n →∞ и величины xn являются ограниченными. Тогда
. Предположим, что m →∞, n →∞ и величины xn являются ограниченными. Тогда .
.
 . Предположим, что m 1→∞, n →∞ и величины an и bn являются ограниченными. Тогда
. Предположим, что m 1→∞, n →∞ и величины an и bn являются ограниченными. Тогда .
. ,
,  .
. ,
, ,
, ,
,
 .
.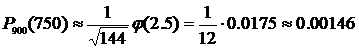 .
.
 .
.
 ,
, .◄
.◄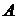 в 100 независимых испытаниях, если вероятность его появления в отдельном испытании
в 100 независимых испытаниях, если вероятность его появления в отдельном испытании  ?
? .
. .
. . По таблице значений функции Гаусса находим x = 1.09. Подставляя это значение в выражение для x, получим
. По таблице значений функции Гаусса находим x = 1.09. Подставляя это значение в выражение для x, получим .
. . ◄
. ◄ .
. . ◄
. ◄ . Имеем
. Имеем
 .
.
 , или
, или  .
. , значит
, значит  . Следовательно, в ресторане должно быть 537 мест. ◄
. Следовательно, в ресторане должно быть 537 мест. ◄


