Обобщённый алгоритм решения задачи линейной оптимизации (линейного программирования) с помощью симплекс-методасостоит в следующем.
На первом шаге задача линейного программирования приводится к канонической форме, которая характеризуется тем, что, во-первых, ограничения имеют вид линейных уравнений. Если в исходной постановке задачи оптимизации присутствуют ограничения-неравенства, то переход от ограничений-неравенств к ограничениям-уравнениям можно осуществить по следующим правилам.
Так, если в системе ограничений присутствует неравенство, у которого левая часть меньше правой, т.е. неравенство вида
ai1x1 + ai2x2 + … + aijxj +… + ainxn ≤ bi,
то к его левой части необходимо прибавить неотрицательную величину xn+i. В таком случае данное неравенство преобразуется в уравнение
ai1x1 + ai2x2 + … + aijxj +… + ainxn + xn+i= bi.
Аналогично, если в системе ограничений присутствует неравенство, у которого левая часть больше правой, т.е. неравенство вида
ai1x1 + ai2x2 + … + aijxj +… + ainxn ≥ bi,
то из его левой части необходимо вычесть неотрицательную величину xn+i . В таком случае данное неравенство преобразуется в уравнение
ai1x1 + ai2x2 + … + aijxj +… + ainxn – xn+i= bi.
Во-вторых, целевая функция должна быть устремлена к минимуму (иными словами, ищется минимум целевой функции). Если в исходной постановке задачи оптими-зации предусматривается отыскание максимума целевой функции, то для отыскания её минимума необходимо умножить целевую функцию на –1.
Тогда задачу линейного программирования в канонической форме можно сформулировать так: найти такие неотрицательные значения переменных x1, x2, …, xn, которые удовлетворяют ограничениям
a11x1 + a12x2 + … + a1jxj +… + a1nxn = b1;
a21x1 + a22x2 + … + a2jxj + … + a2nxn = b2;
…………………………………………
aj1x1 + aj2x2 + … + aijxj + … + ainxn = bi;
…. ……………………………………. (1)
am1x1 + am2x2 + … + amjxj + … + amnxn = bm
и обращают в минимум целевую функцию
L(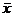 ) = c1x1 + c2x2 + … + cjxj + … + cnxn. (2)
) = c1x1 + c2x2 + … + cjxj + … + cnxn. (2)
При этом коэффициенты aijв системе ограничений и коэффициенты cjцелевой функции могут принимать как положительные, так и отрицательные значения.
В такой постановке задача линейной оптимизации называется основной задачей линейного программирования (ОЗЛП).
Следует отметить, что при m = n данная задача имеет единственное решение и с точки зрения выбора решения не имеет смысла (т.е. по сути, не является оптимизационной). При m<n задача имеет множество решений и, следовательно, существует возможность выбора наилучшего (оптимального) решения.
Совокупность неотрицательных значений переменных x1, x2, …, xn, удовлетворяющих ограничениям (2), называется допустимым решением ОЗЛП, а совокупность всех допустимых решений представляет собой подмножество допустимых решений ОЗЛП. Допустимое решение ОЗЛП в виде совокупности значений 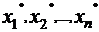 переменных, обеспечивающих минимальное значение целевой функции L(
переменных, обеспечивающих минимальное значение целевой функции L(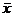 ), называется оптимальным решением ОЗЛП.
), называется оптимальным решением ОЗЛП.
Ввиду того, что m<n, все множество переменных x1, x2, …, xn можно представить в виде двух подмножеств: базисных и свободных переменных. При этом число базисных переменных равно m, а число свободных – соответственно – k = n – m. В качестве свободных обычно принимают переменные x1, x2,…, xk, а в качестве базисных – xk+1, xk+2, …, xk+l, …, xk+m.
Вторым шагом для решения ЗЛП с помощью симплекс-метода является её представление в стандартной форме.
Для этого, во-первых, в системе уравнений-ограничений (1) базисные переменные выражаются через свободные. В результате получается система уравнений вида
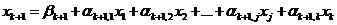 ;
;
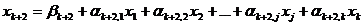 ;
;
............................................................................
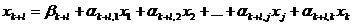 ;
;  (3)
(3)
……………………………………………… 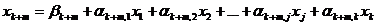 ,
,
где коэффициенты 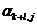 являются комбинациями коэффициентов aijиbi.
являются комбинациями коэффициентов aijиbi.
Целевая функция вида (2) также выражается через свободные переменные и в результате принимает вид
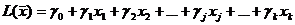 , (4)
, (4)
где коэффициенты 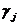 являются комбинациями коэффициентов cj.
являются комбинациями коэффициентов cj.
Затем система уравнений (3) и выражение для целевой функции (4) преобразуются к виду
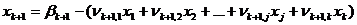 ;
;
…………………………………………………
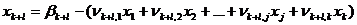 ; (5)
; (5)
…………………………………………………
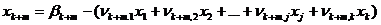 ,
,
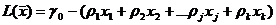 , (6)
, (6)
где 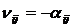 ;
; 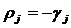 .
.
Третьим шагом является построение исходной симплекс-таблицы на основании соотношений (5) и (6). Данная таблица имеет вид (табл. 1)
Таблица 1
| БП\СП
| СЧ
| 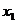
| 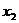
| …
| 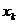
|
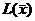
| 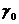
| 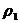
| 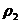
| …
| 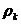
|
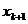
| 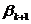
| 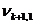
| 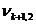
| …
| 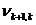
|
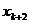
| 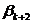
| 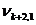
| 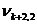
| …
| 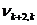
|
| …
| …
| …
| …
| …
| …
|
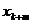
| 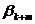
| 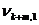
| 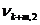
| …
| 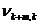
|
Четвёртым шагом является проверка допустимости решения ЗЛП на основе заполненной симплекс-таблицы. В качестве признака допустимости решения ЗЛП выступает требование неотрицательности всех элементов второго столбца (коэффициентов 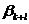 ) симплекс-таблицы (коэффициент
) симплекс-таблицы (коэффициент 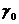 в расчёт не принимается).
в расчёт не принимается).
Если данное требование не выполняется (т.е. среди коэффициентов 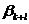 имеется хотя бы один отрицательный), то осуществляется замена базисных переменных на свободные в соответствии с алгоритмом, описанным в приложении 4 лабораторной работы №5. При этом если в ходе поиска допустимого решения возникнет ситуация, когда в симплекс-таблице один или несколько элементов второго столбца отрицательны, и хотя бы в одной строке, соответствующей одному из этих элементов, остальные элементы положительны, то это свидетельствует об отсутствии у ЗЛП допустимого решения.
имеется хотя бы один отрицательный), то осуществляется замена базисных переменных на свободные в соответствии с алгоритмом, описанным в приложении 4 лабораторной работы №5. При этом если в ходе поиска допустимого решения возникнет ситуация, когда в симплекс-таблице один или несколько элементов второго столбца отрицательны, и хотя бы в одной строке, соответствующей одному из этих элементов, остальные элементы положительны, то это свидетельствует об отсутствии у ЗЛП допустимого решения.
После того какполучено допустимое решение ЗЛП, пятым шагом является проверка данного допустимого решения на оптимальность. Признаком оптимальности решения ЗЛП является требование отрицательности всех элементов второй строки (коэффициентов rj) симплекс-таблицы (коэффициент 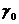 в расчёт не принимается). Если данное требование не выполняется (т.е. среди коэффициентов rj имеется хотя бы один положительный), то осуществляется замена базисных переменных на свободные в соответствии с алгоритмом, описанным в приложении 3 лабораторной работы №5, до тех пор, пока не будет получено единственное оптимальное решение. При этом искомыми оптимальными значениями переменных будут значения базисных переменных второго столбца конечной симплекс-таблицы, а минимальным значением целевой функции – значение
в расчёт не принимается). Если данное требование не выполняется (т.е. среди коэффициентов rj имеется хотя бы один положительный), то осуществляется замена базисных переменных на свободные в соответствии с алгоритмом, описанным в приложении 3 лабораторной работы №5, до тех пор, пока не будет получено единственное оптимальное решение. При этом искомыми оптимальными значениями переменных будут значения базисных переменных второго столбца конечной симплекс-таблицы, а минимальным значением целевой функции – значение 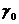 . В принципе, можно решать задачу получения оптимального решения и добиваясь положительности всех элементов второй строки, но в таком случае минимальным значением целевой функции будет значение
. В принципе, можно решать задачу получения оптимального решения и добиваясь положительности всех элементов второй строки, но в таком случае минимальным значением целевой функции будет значение 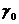 , взятое с отрицательным знаком.
, взятое с отрицательным знаком.
При этом если в ходе поиска оптимального решения возникнет ситуация, когда во второй строке симплекс-таблицы один или несколько элементов равны нулю (коэффициенты rj), а все остальные отрицательны, то это свидетельствует о том, что данная ЗЛП имеет бесчисленное множество оптимальных решений.
Например, если коэффициент r2 = 0, то имеет место выражение для целевой функции 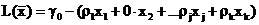 , где переменная x2, а, следовательно, и сама целевая функция могут принимать произвольное значение.
, где переменная x2, а, следовательно, и сама целевая функция могут принимать произвольное значение.
Если же в ходе поиска оптимального решения окажется, что во второй строке симплекс-таблицы один или несколько элементов положительны, а в столбце, соответствующем положительному элементу, остальные элементы (коэффициенты 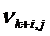 ) отрицательны, то это свидетельствует о том, что данная ЗЛП не имеетоптимального решения.
) отрицательны, то это свидетельствует о том, что данная ЗЛП не имеетоптимального решения.



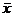 ) = c1x1 + c2x2 + … + cjxj + … + cnxn. (2)
) = c1x1 + c2x2 + … + cjxj + … + cnxn. (2)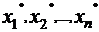 переменных, обеспечивающих минимальное значение целевой функции L(
переменных, обеспечивающих минимальное значение целевой функции L(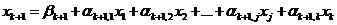 ;
;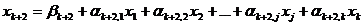 ;
;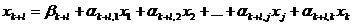 ;
;  (3)
(3)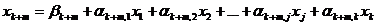 ,
,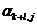 являются комбинациями коэффициентов aijиbi.
являются комбинациями коэффициентов aijиbi.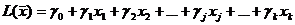 , (4)
, (4)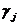 являются комбинациями коэффициентов cj.
являются комбинациями коэффициентов cj.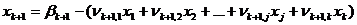 ;
;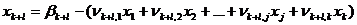 ; (5)
; (5)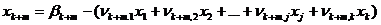 ,
,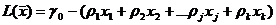 , (6)
, (6)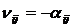 ;
; 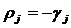 .
.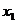
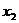
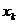
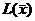
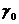
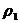
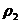
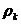
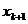
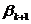
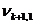
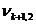
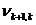
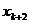
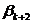
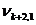
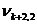
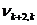
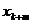
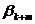
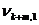
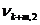
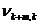
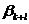 ) симплекс-таблицы (коэффициент
) симплекс-таблицы (коэффициент 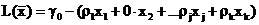 , где переменная x2, а, следовательно, и сама целевая функция могут принимать произвольное значение.
, где переменная x2, а, следовательно, и сама целевая функция могут принимать произвольное значение.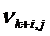 ) отрицательны, то это свидетельствует о том, что данная ЗЛП не имеетоптимального решения.
) отрицательны, то это свидетельствует о том, что данная ЗЛП не имеетоптимального решения.

