Идея метода простых итераций состоит в представлении системы линейных алгебраических уравнений
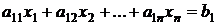 ,
,
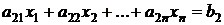 , (1)
, (1)
………………………………,
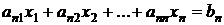 ,
,
в виде
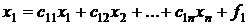 , (2)
, (2)
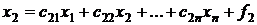 ,
,
……………………………..…..,
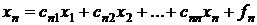 .
.
В матричном виде систему (2) можно записать следующим образом:
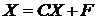 , (3)
, (3)
где
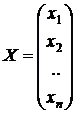 ,
, 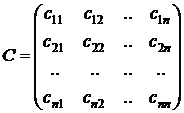 ,
, 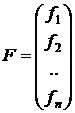 .
.
За нулевое приближение решения системы берётся произвольный вектор
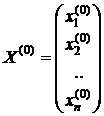 .
.
Затем строятся векторы 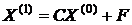 ,
, 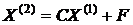 ,…,
,…, 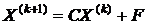 (k = 0,1,… ) посредством выполнения преобразований вида
(k = 0,1,… ) посредством выполнения преобразований вида
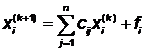 ;
; 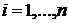 ;
; 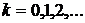 (4)
(4)
Т.е. приближение 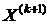 вычисляется по предыдущему приближению
вычисляется по предыдущему приближению 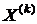 путём подстановки компонент вектора
путём подстановки компонент вектора 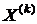 в правую часть уравнений системы (2).
в правую часть уравнений системы (2).
Решением системы уравнений является такой вектор значений 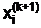 , для которого выполняется условие "i = 1,…,n: ½
, для которого выполняется условие "i = 1,…,n: ½ 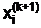 -
- 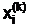 ½<e, где e-заданнаяточностьвычислений.
½<e, где e-заданнаяточностьвычислений.
Предварительным (подготовительным) этапом для применения описанной выше процедуры решения системы линейных алгебраических уравнений вида (1) является приведение её к виду, при котором обеспечивается сходимость итерационного процесса.
Требование сходимости итерационного процесса заключается в выполнении одного из условий
 ;
; 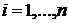 ;
;
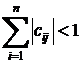 ;
; 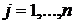 .
.
6. Основныепонятиятеориисравнений: сравнимость чисел по данному модулю, вычет, полный и приведенный набор вычетов по данному модулю. Проиллюстрировать на примере.
Если двум целым числам a и b соответствует один и тот же остаток r от деления на m, то они называются сравнимыми по модулю m, т. е.
a= mq1+ r; b = mq2 + r. (4)
Сравнимость чисел a и b по модулю m записывается как
a = b(modm). (5)
Справедлива также запись
b = a(modm). (6)
Это соотношение справедливо для целых значений a, b и m 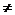 0, тогда и только тогда, когда
0, тогда и только тогда, когда
a = b + km, (7)
где k – некоторое целое.
Таким образом, запись (modm) служит признаком сравнимости чисел по данному модулю m.
Если же записать 29 = 5(mod 12) или 65 = 5(mod 12), то данная ситуация означает операцию приведения чисел 29 и 65 по модулю 12 (т.е., что 5 – это вычет чисел 29 и 65 по модулю 12).
Выражение a = mq + r означает, что для любого целого числа а (а > 0) его вычет r = a(mod m) – это некоторое целое число в интервале от 0 до m – 1. Множество Zm = {0, 1,…, m-1} называется полным набором вычетов по модулю m, а элементы этого множества определяются из соотношения r = a – mq, q = 0, 1, 2, ….
Подмножество 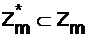 чисел, взаимно простых с m, называется приведенным набором вычетов по модулю m.
чисел, взаимно простых с m, называется приведенным набором вычетов по модулю m.
Например, если m = 10, то Zm= {0, 1, …, 9}, а 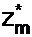 = {1, 3, 7, 9}, так как только числа 1, 3, 7, 9 из множества Zm не имеют с числом 10 общего делителя, большего 1. Если m = 11, Zm= {0, 1, …, 10}, а
= {1, 3, 7, 9}, так как только числа 1, 3, 7, 9 из множества Zm не имеют с числом 10 общего делителя, большего 1. Если m = 11, Zm= {0, 1, …, 10}, а 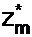 = = {1, 2, …, 10}, поскольку все элементы множества Zm, кроме 0, являются взаимно простыми с числом 11 ввиду того, что оно является простым.
= = {1, 2, …, 10}, поскольку все элементы множества Zm, кроме 0, являются взаимно простыми с числом 11 ввиду того, что оно является простым.
ФункцияЭйлера: понятие и способывычисления. Теорема Эйлера
Функция Эйлера определяется для всех целых положительных чисел а и равна количеству чисел ряда 0, 1, …, а-1, взаимно простых с а. Обозначением функции Эйлера является j(а).
Например, j(5) = 4, j(6) = 2, j(12) = 4. Иными словами, в соответствии с введенными выше определениями, если 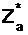 – приведенный набор вычетов по модулю а, то
– приведенный набор вычетов по модулю а, то 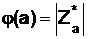 .
.
Очевидно, что для а = m простого согласно (12)
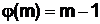 . (13)
. (13)
Функция Эйлера может быть определена исходя из канонического разложения числа вида (1)
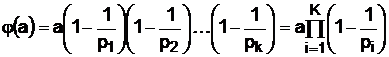 , (14)
, (14)
Или
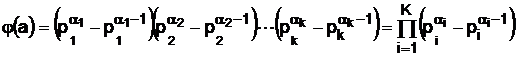 . (15)
. (15)
Например, если а = 60 = 22×3×5, то согласно (14) имеем:
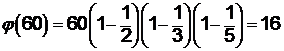 ,
,
либо согласно (15) имеем: 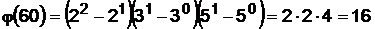 .
.
Функция 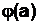 является мультипликативной, т.е.
является мультипликативной, т.е.
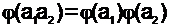 (16)
(16)
в том случае, если числа a1 и a2 взаимно простые.
Из (16), в частности, следует, что, если m = pq, где p и q – простые числа, то, с учётом (13) имеем:
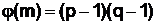 . (17)
. (17)
Теорема Эйлера утверждает, что при m > 1 и 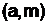 = 1 справедливо соотношение
= 1 справедливо соотношение
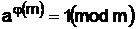 , (18)
, (18)
что также может быть записано как 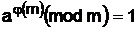 .
.
8. Решениесравненияax = 1(modn) с помощью метода цепныхдробейЕвклида.
Известно, что диафантово уравнение имеет решение в том случае, если a>b (в нашем случае n>a), а также если целочисленные коэффициенты a и b являются взаимно простыми (в нашем случае 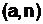 = 1).
= 1).
Уравнение (23) может быть решено на основе метода, базирующегося на разложении отношения 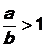 в непрерывную дробь с помощью алгоритма Евклида (см. соотношения (2)). Следовательно, для решения сравнения (21) необходимо представить в виде непрерывной (цепной) дроби отношение
в непрерывную дробь с помощью алгоритма Евклида (см. соотношения (2)). Следовательно, для решения сравнения (21) необходимо представить в виде непрерывной (цепной) дроби отношение 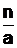 . Так, если данное отношение является рациональной несократимой дробью, то её разложение в непрерывную дробь осуществляется по следующей схеме:
. Так, если данное отношение является рациональной несократимой дробью, то её разложение в непрерывную дробь осуществляется по следующей схеме:
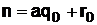 , откуда
, откуда 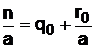 ; (24)
; (24)
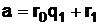 , откуда
, откуда 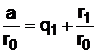 ; (25)
; (25)
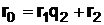 , откуда
, откуда 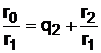 ; (26)
; (26)
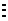
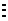
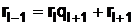 ,
, 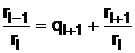 ;
;
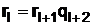 ,
, 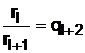 .
.
Второе слагаемое выражения (24) можно получить из (25):
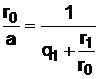 . (27)
. (27)
Тогда, подставляя (26) в (23), получим
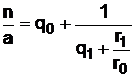 . (28)
. (28)
Далее, по аналогии, отношение 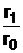 в (25) можно, исходя из (26), представить в виде
в (25) можно, исходя из (26), представить в виде
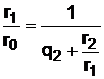 . (29)
. (29)
Подставляя (29) в (28), получим
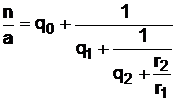 . (30)
. (30)
Действуя далее таким же образом, окончательно получим
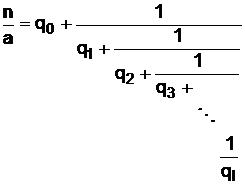 . (31)
. (31)
Числа q1, q2, …, участвующие в разложении дроби 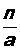 в непрерывную, называются неполными частными, а дроби
в непрерывную, называются неполными частными, а дроби 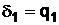 ,
, 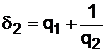 ,
, 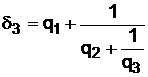 , … называются подходящими.
, … называются подходящими.
Нас в данном случае интересует индекс l при последнем частном цепной дроби, поскольку именно от значения l зависит решение уравнения 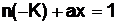 . Оно определяется следующим образом:
. Оно определяется следующим образом:
x= (-1)l×nl-1, (32)
где l – порядок непрерывной дроби, определяющий неполное частное ql, у которого остаток равен 0 (точнее говоря, в этом случае q l является полным частным в отличие от других значений qi).
Коэффициенты nl, al в выражении (31) вычисляются рекурсивно с использованием неполных частных q 1, …, q l -1 следующим образом.
Так, 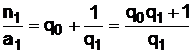 , то есть
, то есть 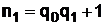 , а
, а 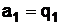 .
.
Далее, 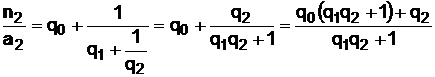 , т.е.
, т.е. 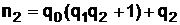 , а
, а  .
.



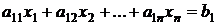 ,
,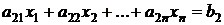 , (1)
, (1)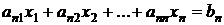 ,
,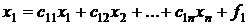 , (2)
, (2)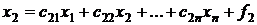 ,
,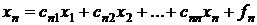 .
.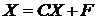 , (3)
, (3)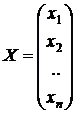 ,
, 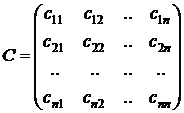 ,
, 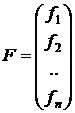 .
.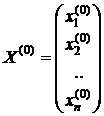 .
.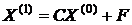 ,
, 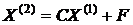 ,…,
,…, 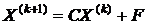 (k = 0,1,… ) посредством выполнения преобразований вида
(k = 0,1,… ) посредством выполнения преобразований вида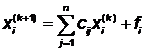 ;
; 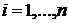 ;
; 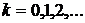 (4)
(4)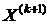 вычисляется по предыдущему приближению
вычисляется по предыдущему приближению 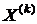 путём подстановки компонент вектора
путём подстановки компонент вектора 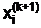 , для которого выполняется условие "i = 1,…,n: ½
, для которого выполняется условие "i = 1,…,n: ½ 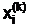 ½<e, где e-заданнаяточностьвычислений.
½<e, где e-заданнаяточностьвычислений. ;
; 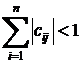 ;
; 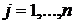 .
.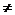 0, тогда и только тогда, когда
0, тогда и только тогда, когда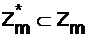 чисел, взаимно простых с m, называется приведенным набором вычетов по модулю m.
чисел, взаимно простых с m, называется приведенным набором вычетов по модулю m.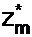 = {1, 3, 7, 9}, так как только числа 1, 3, 7, 9 из множества Zm не имеют с числом 10 общего делителя, большего 1. Если m = 11, Zm= {0, 1, …, 10}, а
= {1, 3, 7, 9}, так как только числа 1, 3, 7, 9 из множества Zm не имеют с числом 10 общего делителя, большего 1. Если m = 11, Zm= {0, 1, …, 10}, а 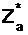 – приведенный набор вычетов по модулю а, то
– приведенный набор вычетов по модулю а, то 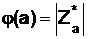 .
.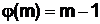 . (13)
. (13)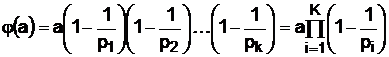 , (14)
, (14)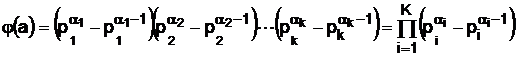 . (15)
. (15)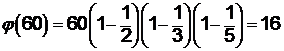 ,
,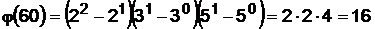 .
.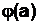 является мультипликативной, т.е.
является мультипликативной, т.е.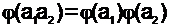 (16)
(16)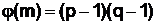 . (17)
. (17)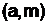 = 1 справедливо соотношение
= 1 справедливо соотношение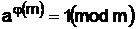 , (18)
, (18)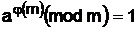 .
.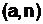 = 1).
= 1).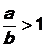 в непрерывную дробь с помощью алгоритма Евклида (см. соотношения (2)). Следовательно, для решения сравнения (21) необходимо представить в виде непрерывной (цепной) дроби отношение
в непрерывную дробь с помощью алгоритма Евклида (см. соотношения (2)). Следовательно, для решения сравнения (21) необходимо представить в виде непрерывной (цепной) дроби отношение 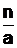 . Так, если данное отношение является рациональной несократимой дробью, то её разложение в непрерывную дробь осуществляется по следующей схеме:
. Так, если данное отношение является рациональной несократимой дробью, то её разложение в непрерывную дробь осуществляется по следующей схеме: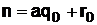 , откуда
, откуда 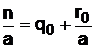 ; (24)
; (24)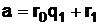 , откуда
, откуда 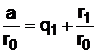 ; (25)
; (25)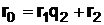 , откуда
, откуда 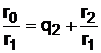 ; (26)
; (26)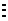
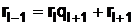 ,
, 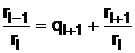 ;
;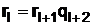 ,
, 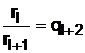 .
.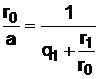 . (27)
. (27)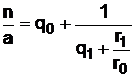 . (28)
. (28)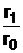 в (25) можно, исходя из (26), представить в виде
в (25) можно, исходя из (26), представить в виде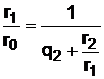 . (29)
. (29)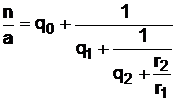 . (30)
. (30)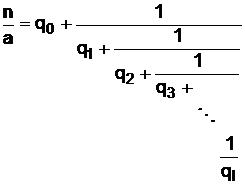 . (31)
. (31)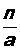 в непрерывную, называются неполными частными, а дроби
в непрерывную, называются неполными частными, а дроби 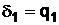 ,
, 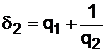 ,
, 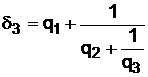 , … называются подходящими.
, … называются подходящими.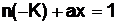 . Оно определяется следующим образом:
. Оно определяется следующим образом: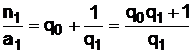 , то есть
, то есть 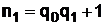 , а
, а 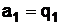 .
.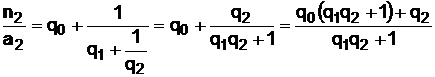 , т.е.
, т.е. 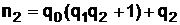 , а
, а  .
.


