LCA (least common ancestor)
Задача LCA (наименьший общий предок) для двух вершин  и
и  в корневом дереве
в корневом дереве  называется узел
называется узел  , который среди всех узлов, являющихся предками как узла
, который среди всех узлов, являющихся предками как узла  , так и
, так и  , имеет наибольшую глубину. Пусть дано корневое дерево
, имеет наибольшую глубину. Пусть дано корневое дерево  . На вход подаются запросы вида
. На вход подаются запросы вида  , для каждого запроса требуется найти их наименьшего общего предка.
, для каждого запроса требуется найти их наименьшего общего предка.
Четыре основных алгоритма:
0. Самый простой, наивный алгоритм для нахождения наименьшего общего предка — вычислить глубину вершин u и v и постепенно подниматься из каждой вершины вверх по дереву, пока не будет найдена общая вершина:
Процедура LCA(u, v):
h1:= depth(u) // depth(x) = глубина вершины x
h2:= depth(v)
while h1 ≠ h2:
if h1 > h2:
u:= parent(u)
h1:= h1 - 1
else:
v:= parent(v)
h2:= h2 - 1
while u ≠ v:
u:= parent(u) // parent(x) = непосредственный предок вершины x
v:= parent(v)
return u
Время работы этого алгоритма составляет O (h), где h — высота дерева. Кроме того, может понадобиться препроцессинг, требующий O (n) времени, для нахождения непосредственного предка для всех вершин дерева и глубины вершин (но, как правило, эта структура на дереве уже имеется) – делается обходом графа.
1. Алгоритм за O(sqrt(H)).
шаг первый: BFS– узнаем глубину дерева и глубину каждой из вершин
Шаг второй: DFS – Делим на уровни длиной sqrt(H) (их всего будет sqrt(H)). Для каждой вершины считаем d[v] = первый предок из предыдущего уровня.
Как считать? Если глубина вершины кратна sqrt(H), значит они или первая, или последняя в уровне – обрабатываем отдельно. Иначе d[v] = d[u], где u – прямой предок v.
Итого предпроцессинг за O(H).
Запрос:
Если вершины на разных уровнях – прыгаем из вершины с меньшим уровнем, пока уровень не будет одинаковым (максимум – O(sqrtH)). Когда достигли одного уровня, то P[v] = P[u], то LCAu,vнаходится между ними и вершиной P[u] = P[v]. Просто поднимаемся вверх (по прямым родителям), пока не окажемся в одной вершине. Если P[u]!= P[v] – максимум за O(sqrt(H)).
Итого алгоритм работает за <O(N), O(sqrtH)>
2. Метод двоичного подъема
Данный алгоритм является on-line (то есть сначала делается препроцессинг, затем алгоритм работает в формате запрос-ответ).
Препроцессинг
Препроцессинг заключается в том, чтобы посчитать функцию:  — номер вершины, в которую мы придем если пройдем из вершины
— номер вершины, в которую мы придем если пройдем из вершины  вверх по подвешенному дереву
вверх по подвешенному дереву 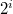 шагов, причем если мы пришли в корень, то мы там и останемся. Для этого сначала обойдем дерево в глубину и для каждой вершины запишем номер ее родителя
шагов, причем если мы пришли в корень, то мы там и останемся. Для этого сначала обойдем дерево в глубину и для каждой вершины запишем номер ее родителя  и глубину вершины в подвешенном дереве
и глубину вершины в подвешенном дереве  . Если
. Если  — корень, то
— корень, то 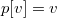 . Тогда для функции
. Тогда для функции 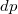 есть рекуррентная формула:
есть рекуррентная формула: 
Ведь 2i-1+2i-1=2i
Для того чтобы отвечать на запросы нам нужны будут только те значения  , где
, где 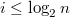 , ведь при больших
, ведь при больших  значение
значение  будет номером корня.
будет номером корня.
Всего состояний динамики 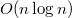 , где
, где 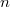 — это количество вершин в дереве. Каждое состояние считается за
— это количество вершин в дереве. Каждое состояние считается за  . Поэтому суммарная сложность времени и памяти препроцессинга —
. Поэтому суммарная сложность времени и памяти препроцессинга — 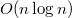 .
.
Ответы на запросы
Ответы на запросы будут происходить за время  . Для ответа на запрос заметим сначала, что если
. Для ответа на запрос заметим сначала, что если  , для некоторых
, для некоторых  и
и  , то
, то  . Поэтому если
. Поэтому если  , то пройдем от вершины
, то пройдем от вершины  на
на 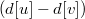 шагов вверх, это и будет новое значение
шагов вверх, это и будет новое значение  и это можно сделать за
и это можно сделать за  . Можно записать число
. Можно записать число 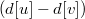 в двоичной системе, это представление этого число в виде суммы степеней двоек,
в двоичной системе, это представление этого число в виде суммы степеней двоек,  и для всех
и для всех  пройти вверх последовательно из вершины
пройти вверх последовательно из вершины  в
в  .
.
Дальше считаем, что  .
.
Если  , то ответ на запрос
, то ответ на запрос  .
.
А если  , то найдем такие вершины
, то найдем такие вершины  и
и 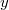 , такие что
, такие что  ,
,  — предок
— предок  ,
, 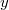 — предок
— предок  и
и  . Тогда ответом на запрос будет
. Тогда ответом на запрос будет  .
.
Научимся находить эти вершины  и
и 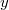 . Для этого сначала инициализируем
. Для этого сначала инициализируем  и
и  . Дальше на каждом шаге находим такое максимальное
. Дальше на каждом шаге находим такое максимальное 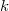 , что
, что  . И проходим из вершин
. И проходим из вершин  и
и 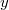 на
на  шагов вверх. Если такого
шагов вверх. Если такого 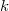 найти нельзя, то значения
найти нельзя, то значения  и
и 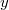 , это те самые вершины, которые нам требуется найти, ведь
, это те самые вершины, которые нам требуется найти, ведь  .
.
Оценим время работы. Заметим, что найденные 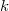 строго убывают. Во-первых, потому что мы находим на каждом шаге максимальное значение
строго убывают. Во-первых, потому что мы находим на каждом шаге максимальное значение 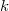 , а во-вторых, два раза подряд мы одно и то же
, а во-вторых, два раза подряд мы одно и то же 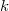 получить не можем, так как тогда получилось бы, что можно пройти
получить не можем, так как тогда получилось бы, что можно пройти 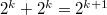 шагов, а значит вместо первого
шагов, а значит вместо первого 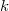 , мы бы нашли
, мы бы нашли 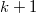 . А значит всего
. А значит всего  значений
значений 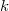 , их можно перебирать в порядке убывания. Сложностьответаназапрос
, их можно перебирать в порядке убывания. Сложностьответаназапрос  .
.
Псевдокод
preprocess()
p:= dfs(0)
for i:= 1.. n
dp[i][0]:= p[i]
for j:= 1.. log(n)
for i:= 1.. n
dp[i][j]:= dp[dp[i][j - 1]][j - 1]
lca(v, u)
if (d[v] > d[u])
swap(v, u)
for i:= log(n).. 0
if (d[u] - d[v] >= 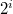 )
)
u:= dp[u][i]
if (v = u)
return v
for i:= log(n).. 0
if (dp[v][i] <> dp[u][i])
v:= dp[v][i]
u:= dp[u][i]
return p[v]
3. Алгоритм с предпроцессингом (Сведение LCA к RMQ)
Для каждой вершины  определим глубину с помощью следующей рекурсивной формулы:
определим глубину с помощью следующей рекурсивной формулы: 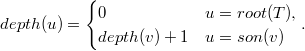
Ясно, что глубина вершины элементарным образом поддерживается во время обхода в глубину.
Запустим обход в глубину из корня, который будет вычислять значения следующих величин:
1. Cписок глубин посещенных вершин 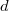 . Глубина текущей вершины добавляется в конец списка при входе в данную вершину, а также после каждого возвращения из её сына.
. Глубина текущей вершины добавляется в конец списка при входе в данную вершину, а также после каждого возвращения из её сына.
2. Список посещений узлов  , строящийся аналогично предыдущему, только добавляется не глубина а сама вершина.
, строящийся аналогично предыдущему, только добавляется не глубина а сама вершина.
3. Значение функции 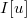 , возвращающей любой индекс в списке глубин
, возвращающей любой индекс в списке глубин 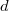 , по которому была записана глубина вершины
, по которому была записана глубина вершины  (например на момент входа в вершину).
(например на момент входа в вершину).
Запрос
Будем считать, что  возвращает индекс минимального элемента в
возвращает индекс минимального элемента в 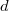 на отрезке
на отрезке  . Тогда ответом на запрос
. Тогда ответом на запрос  , где
, где  , будет
, будет 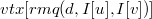 .
.
RMQ через LCA


Дан массив  . Поступают запросы вида
. Поступают запросы вида  , на каждый запрос требуется найти минимум в массиве
, на каждый запрос требуется найти минимум в массиве  , начиная с позиции
, начиная с позиции  и заканчивая позицией
и заканчивая позицией  .
.
Алгоритм
Декартово дерево (англ. сartesian tree) по неявному ключу на массиве  — это бинарное дерево, допускающее следующее рекурсивное построение:
— это бинарное дерево, допускающее следующее рекурсивное построение:
§ Корнем дерева является элемент массива, имеющий минимальное значение  , скажем
, скажем  . Если минимальных элементов несколько, можно взять любой.
. Если минимальных элементов несколько, можно взять любой.
§ Левым поддеревом является декартово дерево на массиве  .
.
§ Правым поддеревом является декартово дерево на массиве  .
.
Здесь и далее  будет также использоваться для обозначения соответствующей вершины дерева.
будет также использоваться для обозначения соответствующей вершины дерева.
Построим декартово дерево на массиве  . Тогда
. Тогда 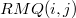 =
=  .
.
Доказательство
| Теорема:
|
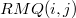 = =  . .
|
| Доказательство:
|

|
Положим 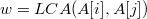 .
Заметим, что .
Заметим, что  и и  не принадлежат одновременно либо правому, либо левому поддереву не принадлежат одновременно либо правому, либо левому поддереву  , потому как тогда бы соответствующий сын находился на большей глубине, чем , потому как тогда бы соответствующий сын находился на большей глубине, чем  , и также являлся предком как , и также являлся предком как  так и так и  , что противоречит определению , что противоречит определению  . Из этого замечанию следует, что . Из этого замечанию следует, что  лежит между лежит между  и и  и, следовательно, принадлежит отрезку и, следовательно, принадлежит отрезку  . По построению мы также знаем, что:
1. Любая вершина дерева имеет свое значение меньшим либо равным значению её детей.
2. Поддерево с корнем в . По построению мы также знаем, что:
1. Любая вершина дерева имеет свое значение меньшим либо равным значению её детей.
2. Поддерево с корнем в  содержит в себе подмассив содержит в себе подмассив  .
Суммируя, получаем, что .
Суммируя, получаем, что  имеет минимальное значение на отрезке, покрывающем имеет минимальное значение на отрезке, покрывающем  , и принадлежит отрезку , и принадлежит отрезку  , отсюда , отсюда  . .
|
|
Сложность
Следующий алгоритм строит декартово дерево за 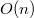 . Используя Сведение задачи LCA к задаче RMQ, получаем: препроцессинг для
. Используя Сведение задачи LCA к задаче RMQ, получаем: препроцессинг для  —
— 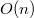 и ответ на запрос —
и ответ на запрос —  . В итоге получили
. В итоге получили  с построением за
с построением за 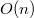 и ответом на запрос за
и ответом на запрос за  .
.
Процесс построения дучи по массиву:
Stack.push(A[0])
For (i = 1; i < n; i++)
If(A[i] >= A[stack.top])
s.top()->right = i;
s.push(i);
else
while(A[i] < A[s.top])
cur = s.top();
s.pop();
i->left = cur;
s.top()->right = I;
s.push(i);
Restricted RMQ
Алгоритм Фарака-Колтона, Бендера (алгоритм Фарах-Колтона, Бендера) — применяется для решения за  времени специального случая задачи RMQ (поиск минимума на отрезке), в котором соседние элементы входной последовательности различаются на ±1. Может быть использован также для решения задачи LCA.
времени специального случая задачи RMQ (поиск минимума на отрезке), в котором соседние элементы входной последовательности различаются на ±1. Может быть использован также для решения задачи LCA.
Вход: последовательность 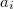 длины
длины  , соседние элементы которой отличаются на ±1.
, соседние элементы которой отличаются на ±1.
Выход: ответы на онлайн запросы вида «позиция минимума на отрезке  ».
».
Алгоритм
Части, из которых состоит ответ на запрос RMQ
Данный алгоритм основывается на методе решения задачи RMQ с помощью разреженной таблицы (sparse table, ST) за  .
.
Чтобы избавиться от логарифма используется предподсчёт ответа для небольших подстрок входной последовательности. Разделим последовательность 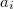 на блоки длины
на блоки длины  . Для каждого блока вычислим минимум на нём и определим
. Для каждого блока вычислим минимум на нём и определим  как позицию минимального элемента в
как позицию минимального элемента в  -том блоке.
-том блоке.
На новой последовательности  построим разреженную таблицу. Теперь для ответа на запрос RMQ
построим разреженную таблицу. Теперь для ответа на запрос RMQ  , если
, если  и
и  находятся в разных блоках, нам необходимо вычислить следующее:
находятся в разных блоках, нам необходимо вычислить следующее:
1. минимум на отрезке от  до конца содержащего
до конца содержащего  блока;
блока;
2. минимум по всем блокам, находящимся между блоками, содержащими  и
и  ;
;
3. минимум от начала блока, содержащего  , до
, до  .
.
Ответом на запрос будет позиция меньшего из эти трёх элементов.
Второй элемент мы уже умеем находить за  с помощью
с помощью  и ST. Осталось научиться находить минимум по отрезку, границы которого не совпадают с границами блоков.
и ST. Осталось научиться находить минимум по отрезку, границы которого не совпадают с границами блоков.
Минимум внутри блока
| Утверждение:
|
Если две последовательности  и и  таковы, что все их элементы на соответствующих позициях различаются на одну и ту же константу (т.е. таковы, что все их элементы на соответствующих позициях различаются на одну и ту же константу (т.е.  ), то любой запрос RMQ даст один и тот же ответ для обеих последовательностей. ), то любой запрос RMQ даст один и тот же ответ для обеих последовательностей.
|
Таким образом, мы можем нормализовать блок, вычтя из всех его элементов первый. Тем самым мы значительно уменьшим число возможных типов блоков.
| Утверждение:
|
Существует  различных типов нормализованных блоков. различных типов нормализованных блоков.
|

|
Соседние элементы в блоках отличаются на ±1. Первый элемент в нормализованном блоке всегда равен нулю. Таким образом, каждый нормализованный блок может быть представлен ±1-вектором длины  . Таких векторов . Таких векторов  . .
|
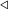
|
Осталось создать  таблиц — по одной для каждого типа блока. В такую таблицу необходимо занести предподсчитанные ответы на все возможные запросы минимума внутри блока соответствующего типа, коих
таблиц — по одной для каждого типа блока. В такую таблицу необходимо занести предподсчитанные ответы на все возможные запросы минимума внутри блока соответствующего типа, коих  . Для каждого блока в
. Для каждого блока в  необходимо заранее вычислить его тип. Таким образом мы получили возможность отвечать на запрос минимума по любой части блока за
необходимо заранее вычислить его тип. Таким образом мы получили возможность отвечать на запрос минимума по любой части блока за  , затратив на предподсчёт
, затратив на предподсчёт  времени.
времени.
Результат
Итого, на предподсчёт требуется  времени и памяти, а ответ на запрос вычисляется за
времени и памяти, а ответ на запрос вычисляется за  .
.



 и
и  в корневом дереве
в корневом дереве  называется узел
называется узел  , который среди всех узлов, являющихся предками как узла
, который среди всех узлов, являющихся предками как узла  , для каждого запроса требуется найти их наименьшего общего предка.
, для каждого запроса требуется найти их наименьшего общего предка. — номер вершины, в которую мы придем если пройдем из вершины
— номер вершины, в которую мы придем если пройдем из вершины 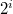 шагов, причем если мы пришли в корень, то мы там и останемся. Для этого сначала обойдем дерево в глубину и для каждой вершины запишем номер ее родителя
шагов, причем если мы пришли в корень, то мы там и останемся. Для этого сначала обойдем дерево в глубину и для каждой вершины запишем номер ее родителя  и глубину вершины в подвешенном дереве
и глубину вершины в подвешенном дереве  . Если
. Если 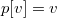 . Тогда для функции
. Тогда для функции 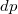 есть рекуррентная формула:
есть рекуррентная формула: 
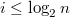 , ведь при больших
, ведь при больших  значение
значение 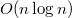 , где
, где 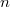 — это количество вершин в дереве. Каждое состояние считается за
— это количество вершин в дереве. Каждое состояние считается за  . Поэтому суммарная сложность времени и памяти препроцессинга —
. Поэтому суммарная сложность времени и памяти препроцессинга —  . Для ответа на запрос заметим сначала, что если
. Для ответа на запрос заметим сначала, что если  , для некоторых
, для некоторых  . Поэтому если
. Поэтому если  , то пройдем от вершины
, то пройдем от вершины 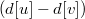 шагов вверх, это и будет новое значение
шагов вверх, это и будет новое значение  и для всех
и для всех  пройти вверх последовательно из вершины
пройти вверх последовательно из вершины  .
. .
. , то ответ на запрос
, то ответ на запрос  , то найдем такие вершины
, то найдем такие вершины  и
и 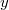 , такие что
, такие что  ,
,  . Тогда ответом на запрос будет
. Тогда ответом на запрос будет  .
. и
и  . Дальше на каждом шаге находим такое максимальное
. Дальше на каждом шаге находим такое максимальное 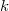 , что
, что  . И проходим из вершин
. И проходим из вершин  шагов вверх. Если такого
шагов вверх. Если такого  .
.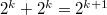 шагов, а значит вместо первого
шагов, а значит вместо первого 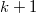 . А значит всего
. А значит всего 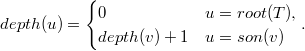
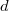 . Глубина текущей вершины добавляется в конец списка при входе в данную вершину, а также после каждого возвращения из её сына.
. Глубина текущей вершины добавляется в конец списка при входе в данную вершину, а также после каждого возвращения из её сына. , строящийся аналогично предыдущему, только добавляется не глубина а сама вершина.
, строящийся аналогично предыдущему, только добавляется не глубина а сама вершина.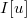 , возвращающей любой индекс в списке глубин
, возвращающей любой индекс в списке глубин  возвращает индекс минимального элемента в
возвращает индекс минимального элемента в  . Тогда ответом на запрос
. Тогда ответом на запрос  , где
, где  , будет
, будет 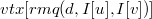 .
.

 . Поступают запросы вида
. Поступают запросы вида  , на каждый запрос требуется найти минимум в массиве
, на каждый запрос требуется найти минимум в массиве  , начиная с позиции
, начиная с позиции  . Если минимальных элементов несколько, можно взять любой.
. Если минимальных элементов несколько, можно взять любой. .
. .
.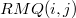 =
=  .
.
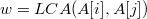 .
Заметим, что
.
Заметим, что  не принадлежат одновременно либо правому, либо левому поддереву
не принадлежат одновременно либо правому, либо левому поддереву  . Из этого замечанию следует, что
. Из этого замечанию следует, что  . По построению мы также знаем, что:
1. Любая вершина дерева имеет свое значение меньшим либо равным значению её детей.
2. Поддерево с корнем в
. По построению мы также знаем, что:
1. Любая вершина дерева имеет свое значение меньшим либо равным значению её детей.
2. Поддерево с корнем в  .
.
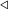
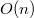 . Используя Сведение задачи LCA к задаче RMQ, получаем: препроцессинг для
. Используя Сведение задачи LCA к задаче RMQ, получаем: препроцессинг для  с построением за
с построением за  времени специального случая задачи RMQ (поиск минимума на отрезке), в котором соседние элементы входной последовательности различаются на ±1. Может быть использован также для решения задачи LCA.
времени специального случая задачи RMQ (поиск минимума на отрезке), в котором соседние элементы входной последовательности различаются на ±1. Может быть использован также для решения задачи LCA.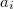 длины
длины  , соседние элементы которой отличаются на ±1.
, соседние элементы которой отличаются на ±1. ».
». .
. . Для каждого блока вычислим минимум на нём и определим
. Для каждого блока вычислим минимум на нём и определим  как позицию минимального элемента в
как позицию минимального элемента в  и
и  таковы, что все их элементы на соответствующих позициях различаются на одну и ту же константу (т.е.
таковы, что все их элементы на соответствующих позициях различаются на одну и ту же константу (т.е.  ), то любой запрос RMQ даст один и тот же ответ для обеих последовательностей.
), то любой запрос RMQ даст один и тот же ответ для обеих последовательностей.
 различных типов нормализованных блоков.
различных типов нормализованных блоков.
 . Таких векторов
. Таких векторов  .
.
 . Для каждого блока в
. Для каждого блока в  времени.
времени. времени и памяти, а ответ на запрос вычисляется за
времени и памяти, а ответ на запрос вычисляется за 


